Classes of association rules short overview Jan Rauch

Classes of association rules short overview Jan Rauch, Department of Knowledge and Information Engineering University of Economics, Prague 1

Classes of association rules – overview n Introduction, classes of rules and quantifiers n Implicational quantifiers n Deduction rules for implicational quantifiers n Tables of critical frequencies for implicational quantifiers n - double implication 4 ft quantifiers n - equivalence 4 ft quantifiers n 4 ft quantifiers with F-property 2

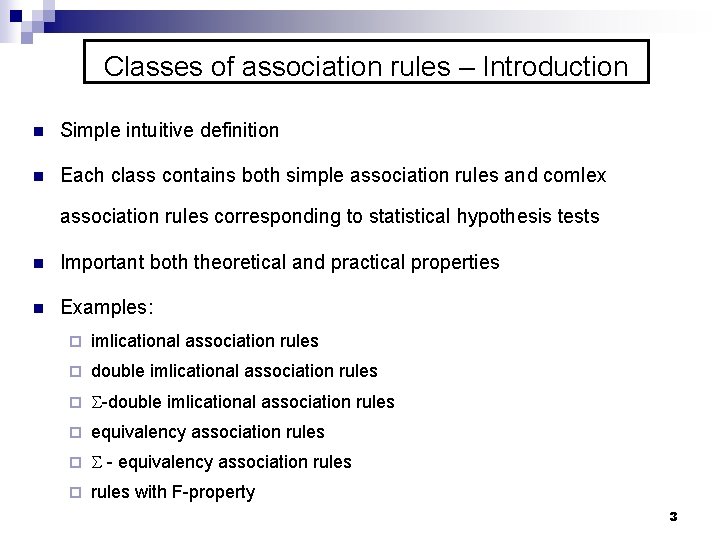
Classes of association rules – Introduction n Simple intuitive definition n Each class contains both simple association rules and comlex association rules corresponding to statistical hypothesis tests n Important both theoretical and practical properties n Examples: ¨ imlicational association rules ¨ double imlicational association rules ¨ -double imlicational association rules ¨ equivalency association rules ¨ - equivalency association rules ¨ rules with F-property 3

Literature Hájek, P. - Havránek T. : Mechanising Hypothesis Formation – Mathematical Foundations for a General Theory. Berlin – Heidelberg - New York, Springer-Verlag, 1978, 396 pp, http: //www. cs. cas. cz/~hajek/guhabook/ Rauch, J. : Logic of Association Rules. Applied Intelligence, 2005, No. 22, 9 -28 Rauch, J. : Classes of Association Rules, An Overview. In: LIN, T. Y. Ying, X. (Ed. ): Foundation of Semantic Oriented Data and Web Mining. Proceedings of an ICDM 2005 Workshop, IEEE Houston 2005. pp 68 – 74. http: //www. cs. sjsu. edu/faculty/tylin/ICDM 05/proceeding. pdf 4

Classes of 4 ft-quantifiers Association rule belongs to the class of association rules if and only if the 4 ft-quantifier belongs to the class of 4 ft-quantifiers Examples: n association rule is implicational iff is implicational n association rule is -double implicational iff is -double implicational n association rule is - equivalency iff is - equivalency 5

* is implicational quantifier M M’ a c b d a’ c’ b’ d’ M’ is better from the point of view of implication: a’ a b’ b If *(a, b, c, d) = 1 and a’ a b’ b then *(a’, b’, c’, d’) = 1 Truth Preservation Condition for implicational quantifiers: TPC : a’ a b’ b * is implicational: If *(a, b, c, d) = 1 and TPC then *(a’, b’, c’, d’) = 1 6

Implication quantifiers – examples (1) Founded implication: p, B (a, b, c, d) = 1 iff a’ a b’ b: Founded 2 b - implication: p, B (a, b, c, d) = 1 iff 7

Implication quantifiers – examples (2) Lower critical implication for 0 < p 1, 0 0. 5: !p; (a, b, c, d) = 1 iff The rule !p; corresponds to the statistical test (on the level ) of the null hypothesis H 0: P( | ) p against the alternative one H 1: P( | ) > p. Here P( | ) is the conditional probability of the validity of under the condition . a’ a b’ b: 8

Deduction rules (1) Is the deduction rule M A A E a c E b d correct? M E F (E F) A a’ b’ A c’ d’ we see: a’ a b’ b and TPC thus if 0. 9, 50(a, b, c, d) = 1 then also 0. 9, 50(a, b, c, d) = 1 Yes, the deduction rule is correct. 9

Deduction rules (2) Is the deduction rule M A A E a c E b d correct? M E F (E F) A a’ b’ A c’ d’ we see: a’ a b’ b and it is TPC and thus if !0. 95, 0. 05(a, b, c, d) = 1 then also !0. 95, 0. 05(a, b, c, d) = 1 Yes, the deduction rule is correct. 10

Deduction rules (3) Additional correct deduction rules (prove it home): Question: * implication quantifier: iff ? ? ? 11

Deduction rules – two notions Associated propositional formula ( ) associated to Boolean attribute : Rule p, B e. g. A B C p, B D E F A, B, C, B, D, E, F are Boolean attributes ( ): Boolean attributes propositional variables ( ) = A B C ( ) = D E F A, B, C, D, E, F are propositional variables, we can decide if ( ) is a tautology 12

Deduction rules – two notions Implicational quantifier is interesting: I is a – dependent , b – dependent and (0, 0, c, d) = 0 is a - dependent if exists a, a’, b, c, d : (a, b, c, d) (a’, b, c, d) 0. 9, 50, !0. 9, 0. 05 are interesting implication quantifiers 13

Correct Deduction Rules is the correct deduction rule iff 1) or 2) are satisfied: 1) both (X) (Y) (X’) (Y’) and (X’) (Y’) (X) (Y) are tautologies 2) (X) (Y) is a tautology 14

Correct Deduction Rules Example: is correct because of A B E A (E B) and A ( E B) A B E are tautologies 15

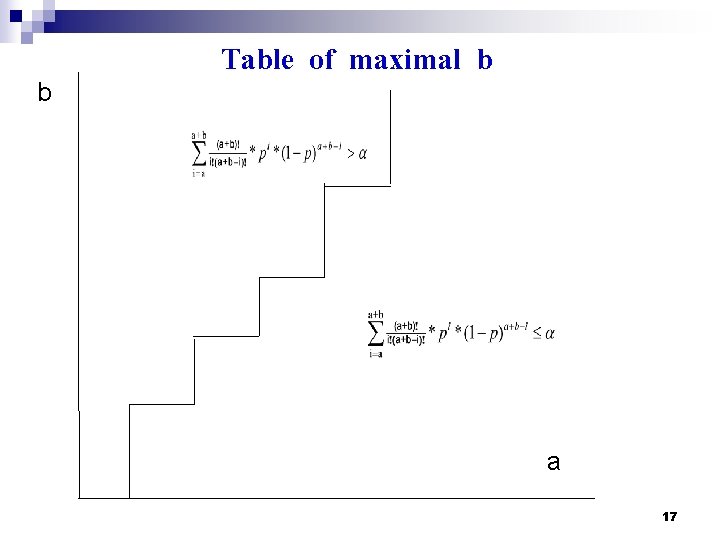
Table of Critical Frequencies implication quantifier: if *(a, b, c, d) = 1 and a’ a b’ b then *(a’, b’, c’, d’) = 1 * is c, d independent, thus *(a, b) instead of *(a, b, c, d) Table of maximal b for *: Tb *(a) = min {e| *(a, e) = 0} *(a, b)= 1 iff b < Tb * (a) 16

Table of maximal b b a 17

Class of - double implication 4 ft quantifiers M X X Y a c Y b d True Preservation Condition: M’ X X Y a’ c’ Y b’ d’ a’ a b’ + c’ b + c example: X p Y a/(a + b + c) p TCF: Tb *(a) = min{b+c| *(a, b, c) = 0} *(a, b, c)= 1 iff b + c < Tb * (a) is correct iff. . . 18

Class of - equivalence 4 ft quantifiers M X X Y a c Y b d True Preservation Condition: M’ X X Y a’ c’ Y b’ d’ a’ + d’ a + d b’ + c’ b + c example: X p Y (a + d)/(a+b+c+d) p TCF: Tb *(F) = min {b+c | *(a, b, c, d)=0 a+d=F} *(a, b, c, d)= 1 iff b + c < Tb *(a + d) is correct iff. . . 19

4 ft quantifiers with F-property has the F-property if it satisfies 1) If (a, b, c, d) = 1 and b c – 1 0 then (a, b+1, c-1, d) = 1 2) If (a, b, c, d) = 1 and c b – 1 0 then (a, b -1, c+1, d) = 1 If is symmetrical and has the F-property then there is a function T (a, d, n) such that for a+b+c+d = n is (a, b, c, d) = 1 iff | b-c | T (a, d, n) Fisher’s quantifier and 2 quantifier have the F-property 20

AA - quantifier has F-property 21