Class structures are classified according to their secondary


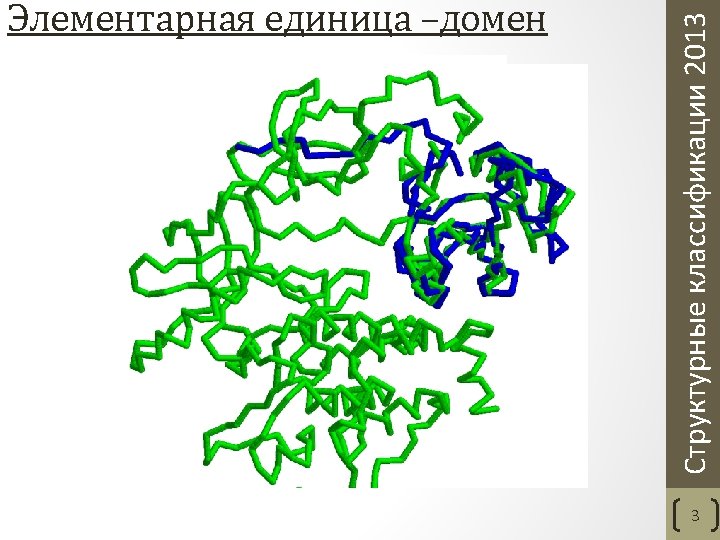



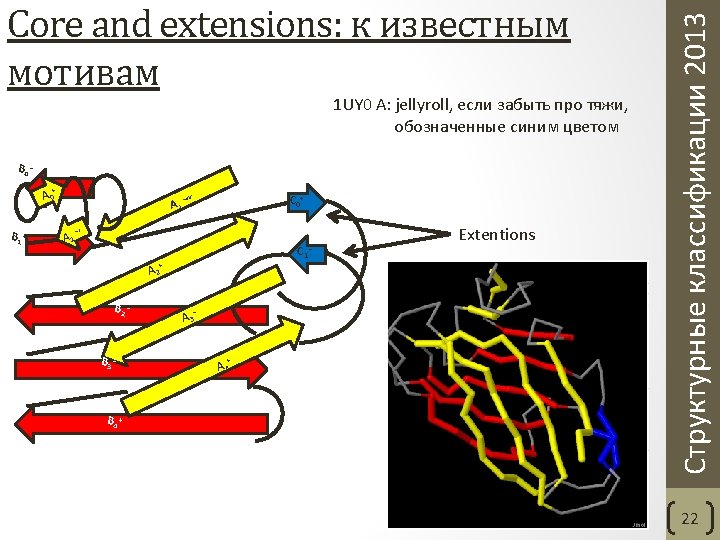
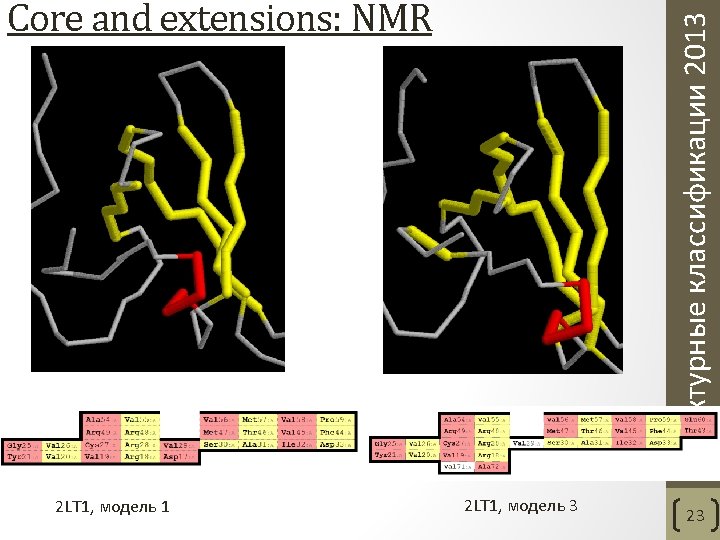








- Slides: 37






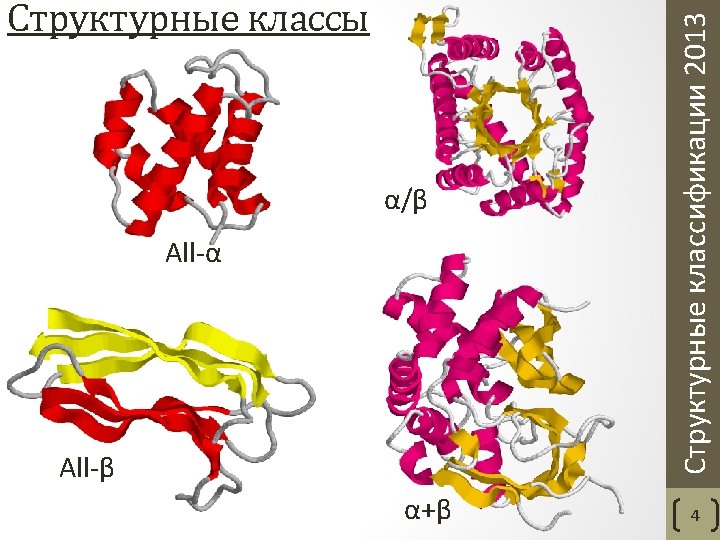
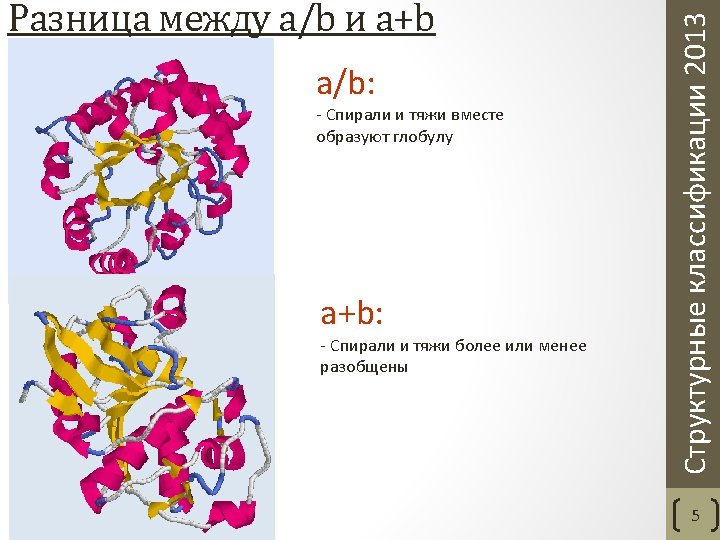
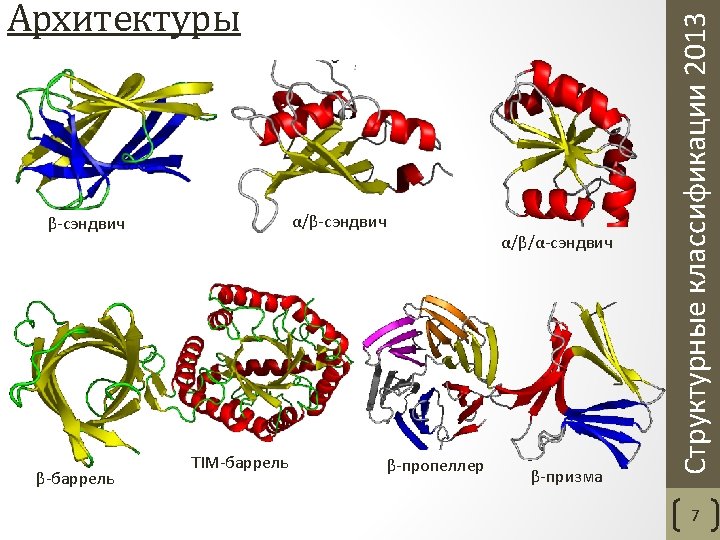
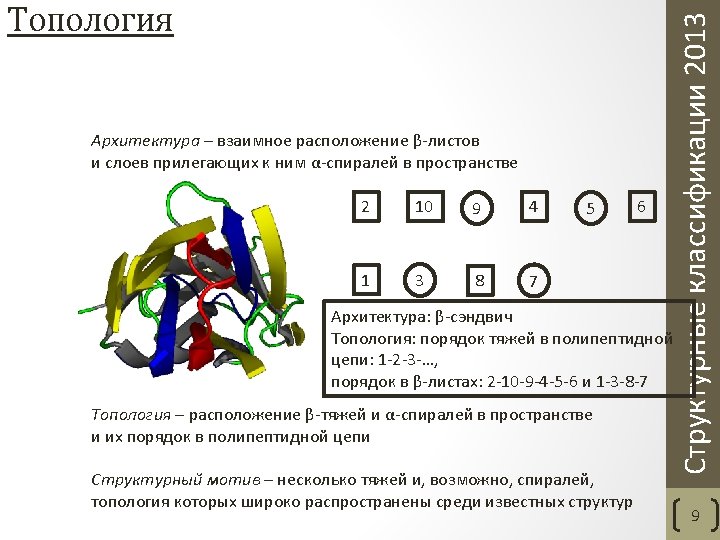
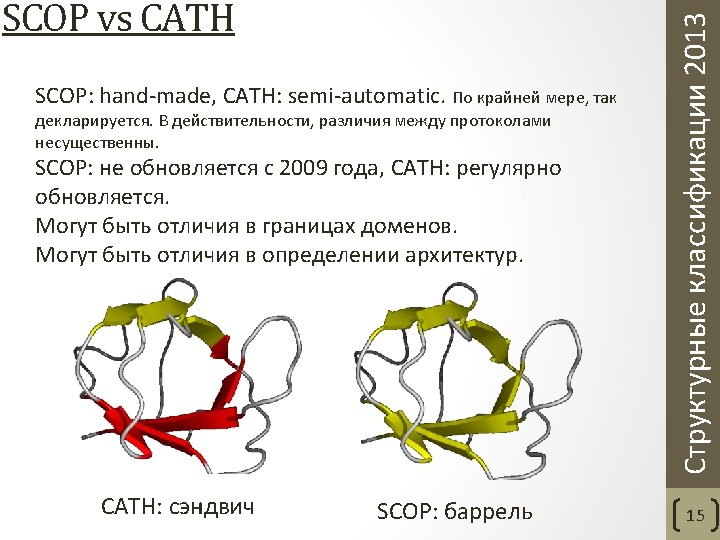
• Class - structures are classified according to their secondary structure composition (mostly alpha, mostly beta, mixed alpha/beta or few secondary structures). • Architecture - structures are classified according to their overall shape as determined by the orientations of the secondary structures in 3 D space but ignores the connectivity between them. • Topology (fold family) - structures are grouped into fold groups at this level depending on both the overall shape and connectivity of the secondary structures. • Homologous superfamily - this level groups together protein domains which are thought to share a common ancestor and can therefore be described as homologous. Orengo C. A. et al. CATH--a hierarchic classification of protein domain structures. Structure. 1997 5(8). Структурные классификации 2013 CATH. Уровни классификации 6





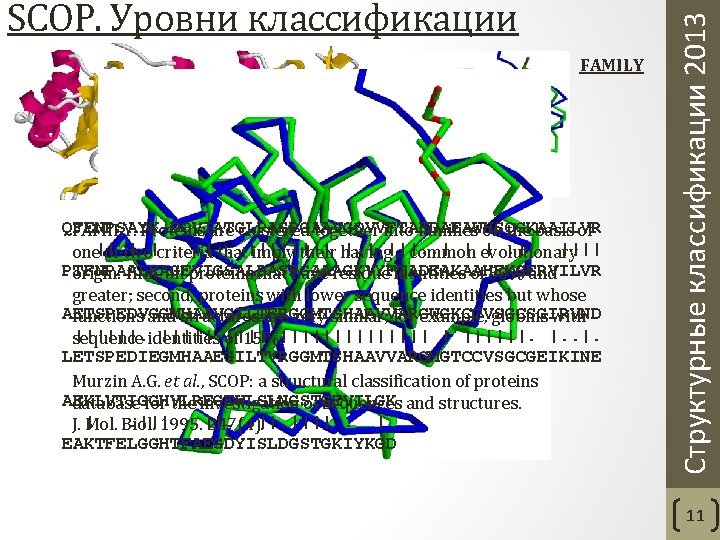
FAMILY QFENPSAYK-DQVIATGLPASPGAAVGQVVFTAEDAEAWHSQGKAAILVR FAMILY. Proteins are clustered together into families on the basis of. . |||| |. | |||. . | | evolutionary |. | |||| one||. | of two|criteria that imply their having a common PTFNPAALKAGEVIGSALPASPGAAAGKVYFTADEAKAAHEKGERVILVR origin: first, all proteins that have residue identities of 30% and greater; second, proteins with lower sequence identities but whose AETSPEDVGGMHAAVGILTERGGMTSHAAVVARGWGKCCVSGCSGIRVND functions and structures are very similar; for example, globins with ||||||. identities ||||| of |||| sequence 15%. ||||||| | ||||||. |. LETSPEDIEGMHAAEGILTVRGGMTSHAAVVARGMGTCCVSGCGEIKINE Murzin A. G. et al. , SCOP: a structural classification of proteins AEKLVTIGGHVLREGEWLSLNGSTGEVILGK database for the investigation of sequences and structures. . ||||. | J. | Mol. Biol. 1995. 247(4). EAKTFELGGHTFAEGDYISLDGSTGKIYKGD Структурные классификации 2013 SCOP. Уровни классификации 11

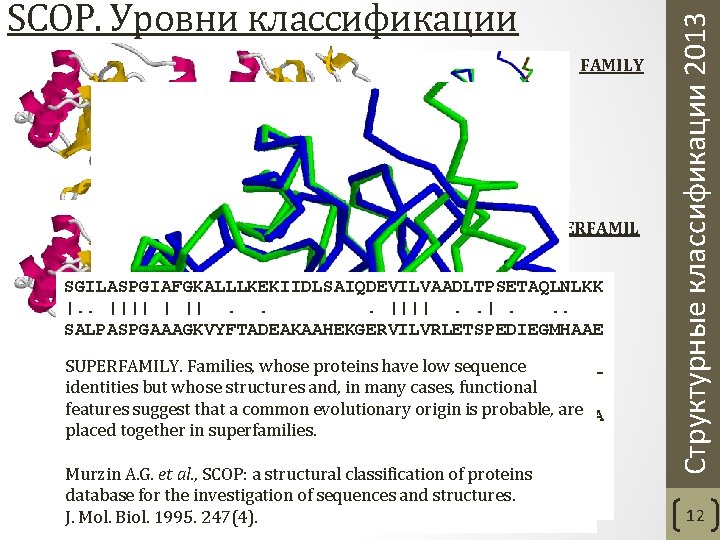
FAMILY SUPERFAMIL Y SGILASPGIAFGKALLLKEKIIDLSAIQDEVILVAADLTPSETAQLNLKK |. . |||| | ||. . . ||||. . . SALPASPGAAAGKVYFTADEAKAAHEKGERVILVRLETSPEDIEGMHAAE SUPERFAMILY. Families, whose proteins have low sequence VLGFITDAGGRTSHTSIMARSLELPAIVGTGSV-------TSQVK-N--identities structures and, . in many cases, functional |. . | but ||whose |||. . | |. |. . . features suggest that a common evolutionary origin is probable, are --GILTVRGGMTSHAAVVARGMGTCCVSGCGEIKINEEAKTFELGGHTFA placed together in superfamilies. -DDYLILDAVNNQVYVNP Murzin SCOP: a structural classification of proteins. ||. A. G. ||. et al. , . . | database for the investigation of sequences and structures. EGDYISLDGSTGKIYKGD J. Mol. Biol. 1995. 247(4). Структурные классификации 2013 SCOP. Уровни классификации 12

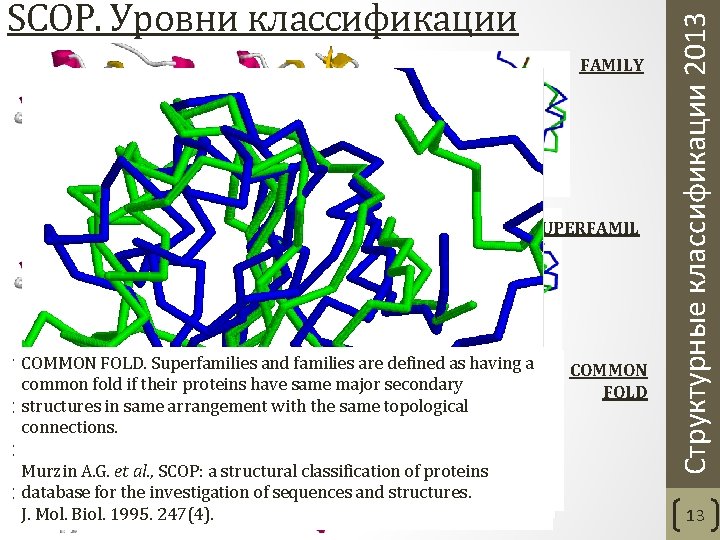
FAMILY SUPERFAMIL Y COMMON FOLD. Superfamilies and families are defined as having a VHGAVRDAAALRGIDIGIKALGTNP---R-KS--T---KTGAGERDVEIT COMMON common fold if their proteins. |. || || have. . | same major | |secondary. | |. . . FOLD structures in same arrangement with the same topological LHPTFNPAALKAGEVIG-SALPASPGAAAGKVYFTADEAKAAHEKGERVI connections. LGGVTFVPGDI-AYSDDDGIIVV et al. , a structural classification of proteins |Murzin. A. G. | ||. SCOP: . ||. | database for the investigation of sequences and structures. LVRLETSPEDIEGMHAAEGILTV J. Mol. Biol. 1995. 247(4). Скрипт commfold. spt Структурные классификации 2013 SCOP. Уровни классификации 13

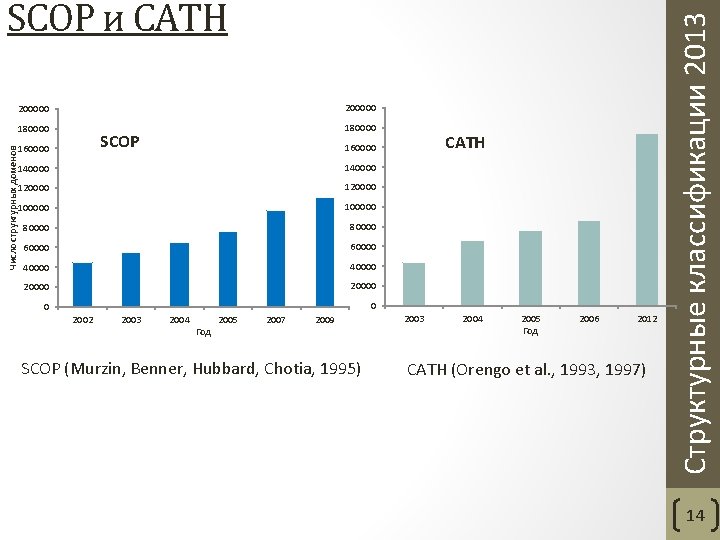
200000 180000 SCOP 160000 CATH 160000 140000 120000 100000 80000 60000 40000 20000 0 0 2002 2003 2004 Год 2005 2007 2009 SCOP (Murzin, Benner, Hubbard, Chotia, 1995) 2003 2004 2005 Год 2006 2012 CATH (Orengo et al. , 1993, 1997) Структурные классификации 2013 Число структурных доменов SCOP и CATH 14




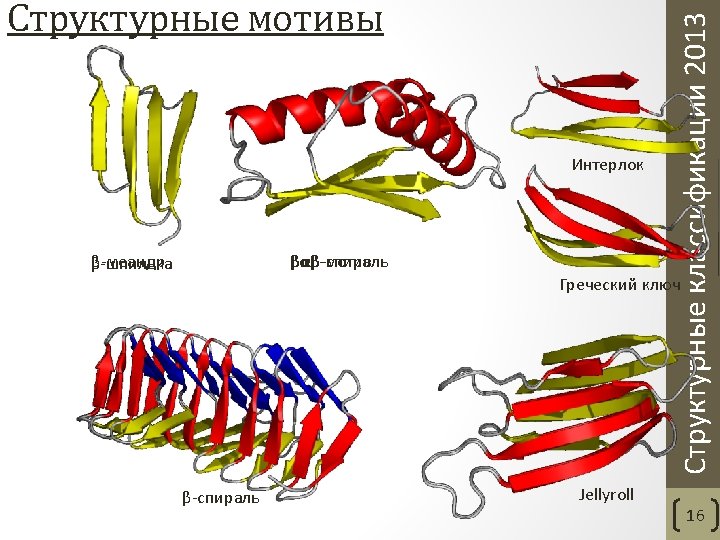
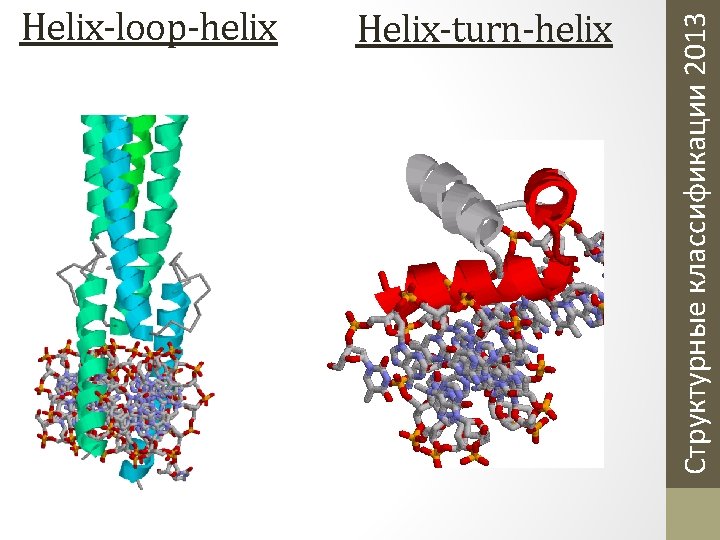
Helix-turn-helix Структурные классификации 2013 Helix-loop-helix






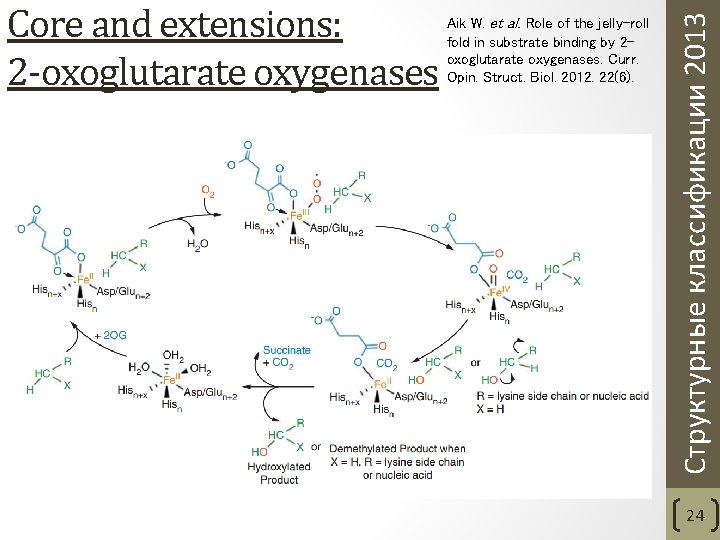
Aik W. et al. Role of the jelly-roll fold in substrate binding by 2 oxoglutarate oxygenases. Curr. Opin. Struct. Biol. 2012. 22(6). Структурные классификации 2013 Core and extensions: 2 -oxoglutarate oxygenases 24

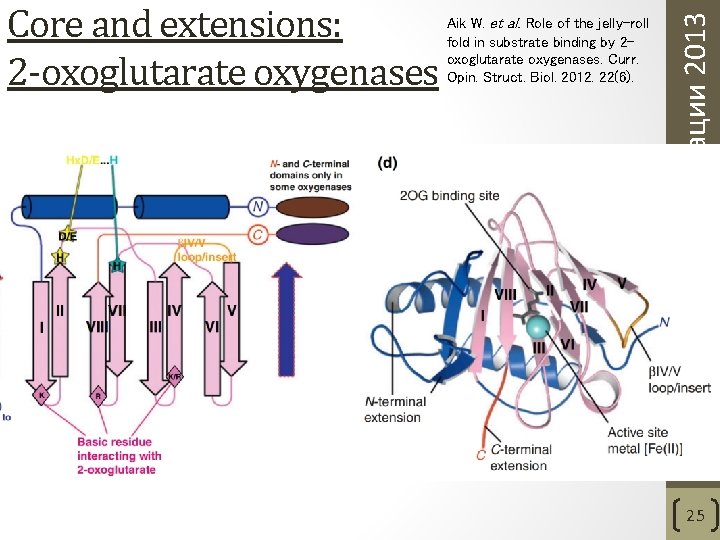
Aik W. et al. Role of the jelly-roll fold in substrate binding by 2 oxoglutarate oxygenases. Curr. Opin. Struct. Biol. 2012. 22(6). Структурные классификации 2013 Core and extensions: 2 -oxoglutarate oxygenases 25

Aik W. et al. Role of the jelly-roll fold in substrate binding by 2 oxoglutarate oxygenases. Curr. Opin. Struct. Biol. 2012. 22(6). Скрипт 1 bk 0_3 o 2 g_jr. spt Структурные классификации 2013 Core and extensions: 2 -oxoglutarate oxygenases 26




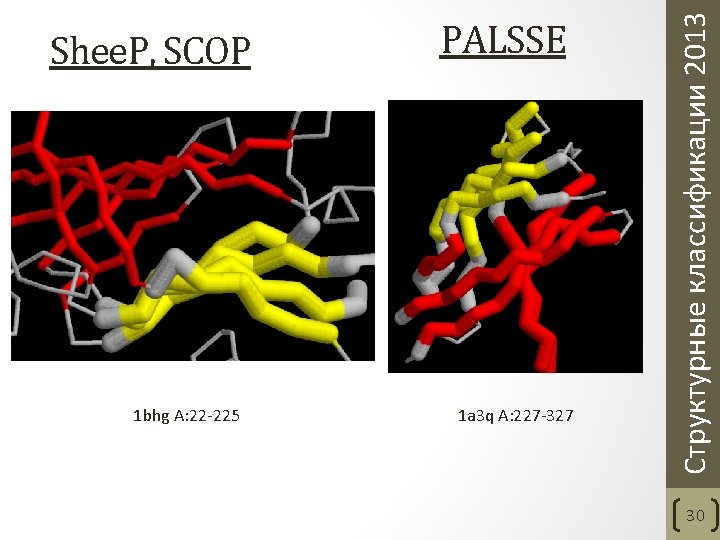
1 bhg A: 22 -225 PALSSE 1 a 3 q A: 227 -327 Структурные классификации 2013 Shee. P, SCOP 30

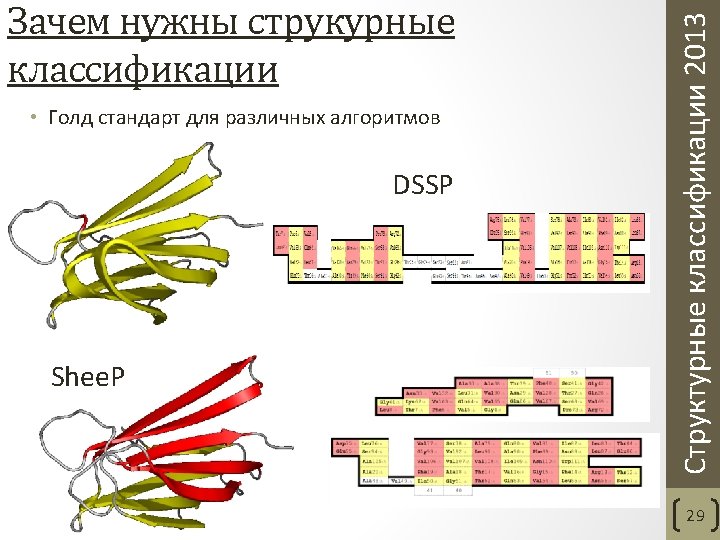
Aksianov, Alexeevski. Shee. P: A Tool for Description of β-Sheets in Protein 3 D Structures. Journal of Bioinformatics and Computational Biology, 2012. 10(2) Структурные классификации 2013 Частота ошибок, допускаемых программами DSSP, Stride и Shee. P 31


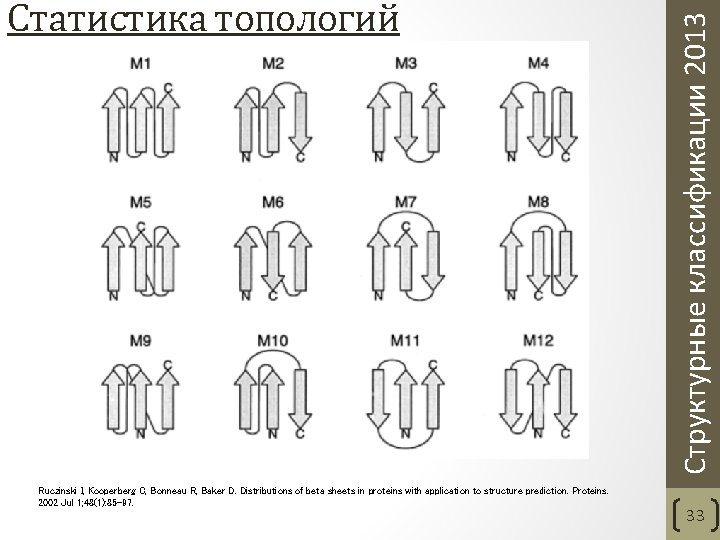
Ruczinski I, Kooperberg C, Bonneau R, Baker D. Distributions of beta sheets in proteins with application to structure prediction. Proteins. 2002 Jul 1; 48(1): 85 -97. Структурные классификации 2013 Статистика топологий 33

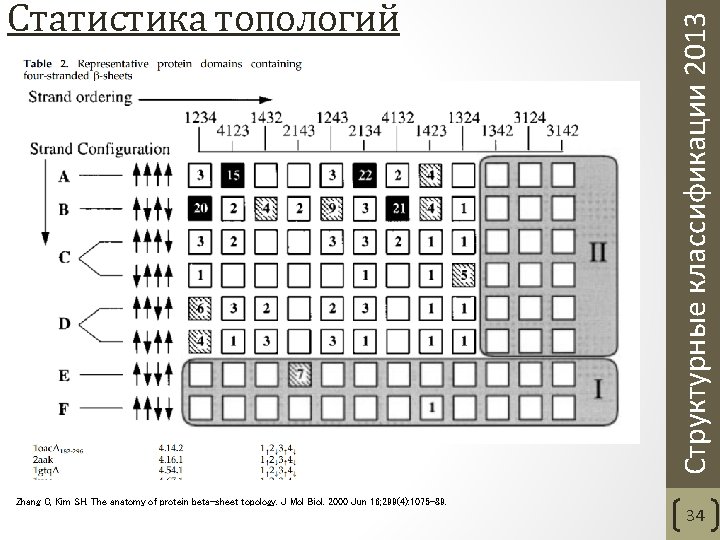
Zhang C, Kim SH. The anatomy of protein beta-sheet topology. J Mol Biol. 2000 Jun 16; 299(4): 1075 -89. Структурные классификации 2013 Статистика топологий 34

Ruczinski I, Kooperberg C, Bonneau R, Baker D. Distributions of beta sheets in proteins with application to structure prediction. Proteins. 2002 Jul 1; 48(1): 85 -97. Структурные классификации 2013 Статистика топологий: Rozetta 35

Ruczinski I, Kooperberg C, Bonneau R, Baker D. Distributions of beta sheets in proteins with application to structure prediction. Proteins. 2002 Jul 1; 48(1): 85 -97. Структурные классификации 2013 Статистика топологий: Rozetta 36
