Class 8 The Capital Asset Pricing Model Efficient

Class 8 The Capital Asset Pricing Model

Efficient Portfolios with Multiple Assets E[r] Efficient Frontier Asset Portfolios Asset 1 of other Portfolios of assets 2 Asset 1 and Asset 2 Minimum-Variance Portfolio 0 s

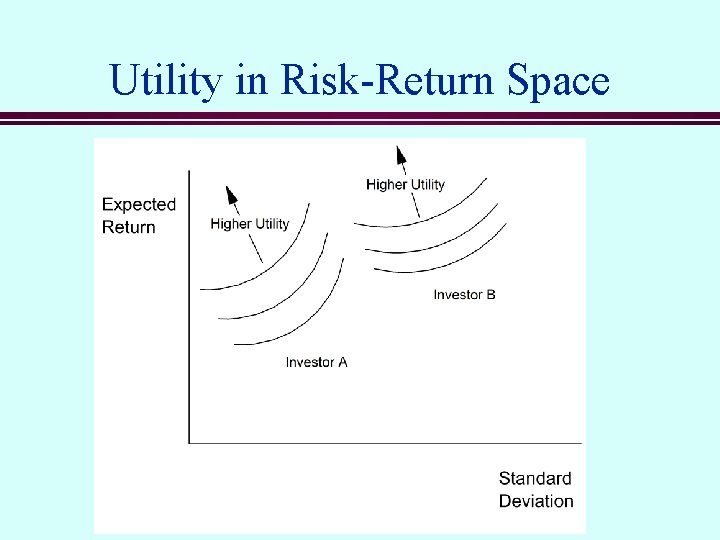
Utility in Risk-Return Space

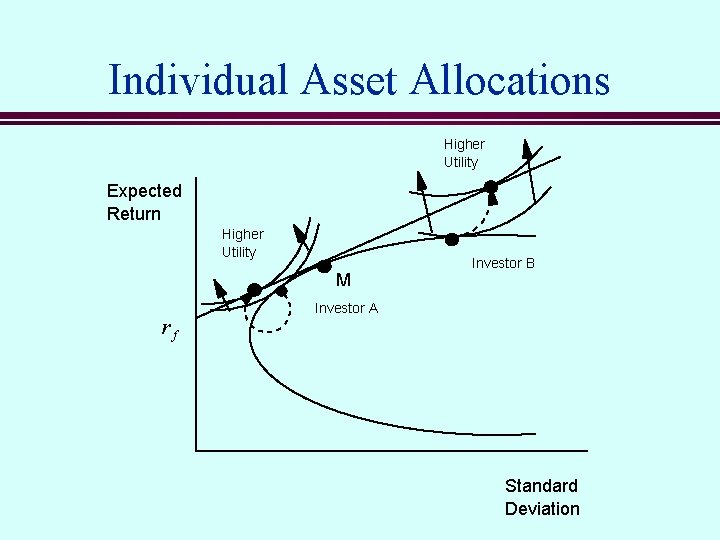
Individual Asset Allocations Expected Return Investor B Investor A Standard Deviation

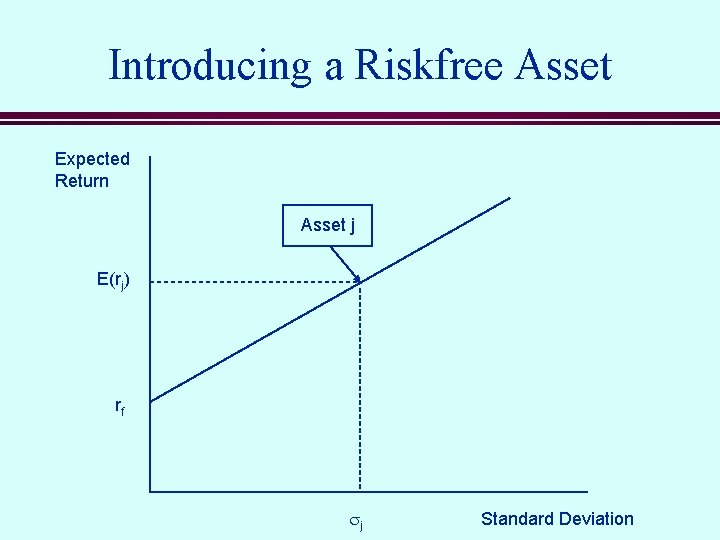
Introducing a Riskfree Asset n n Suppose we introduce the opportunity to invest in a riskfree asset. How does this alter investors’ portfolio choices? The riskfree asset has a zero variance and a zero covariance with every other asset (or portfolio). s var(rf) = 0. s cov(rf, rj) = 0 for all j. n What is the expected return and variance of a portfolio consisting of a fraction af of the riskfree asset and (1 -af) of the risky asset (or portfolio)?

Introducing a Riskfree Asset n Expected Return n Variance and Standard Deviation

Introducing a Riskfree Asset Expected Return Asset j E(rj) rf sj Standard Deviation

Introducing a Riskless Asset Expected Return a=-1 a = 0. 5 E[r. M ] M a= 0 rf a=1 0 s. M Standard Deviation

Individual Asset Allocations Higher Utility Expected Return Higher Utility M rf Investor B Investor A Standard Deviation

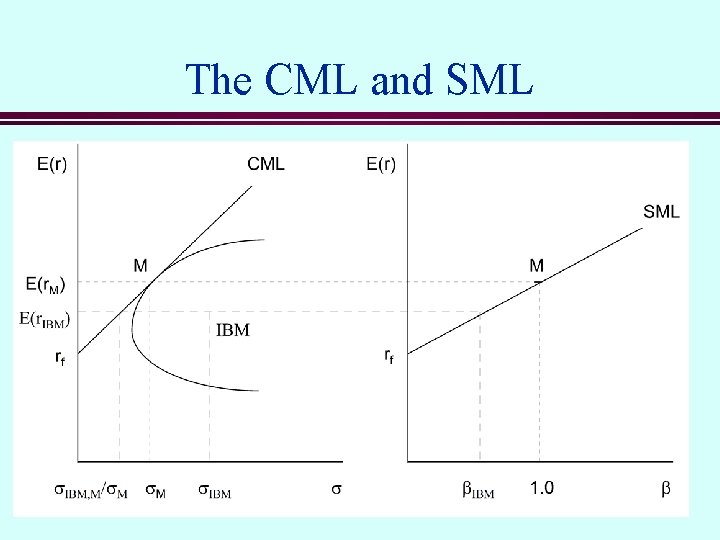
The Capital Market Line Expected Return E [ rm ] E [ r. IBM ] M A IBM rf 14243 1444 424444 3 Systematic Diversifiable Risk Standard Deviation

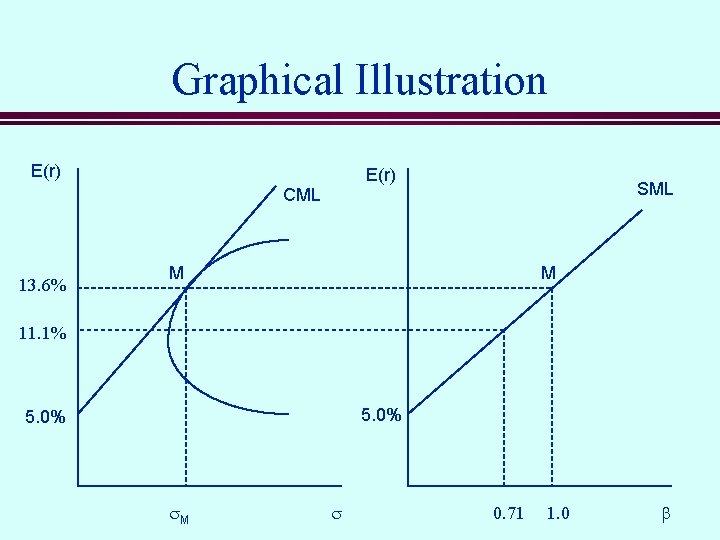
The Capital Market Line n The CML gives the tradeoff between risk and return for portfolios consisting of the riskfree asset and the tangency portfolio M. The equation of the CML is: n Portfolio M is the market portfolio. n

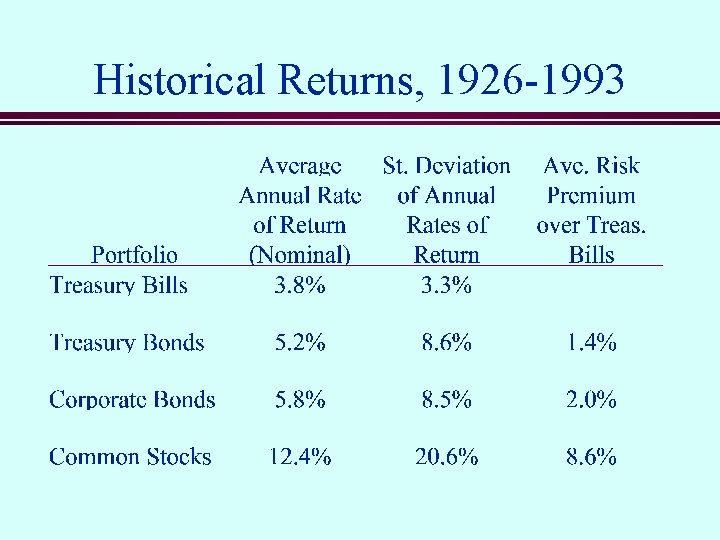
Historical Returns, 1926 -1993

Relationship Between Risk and Return for Individual Assets n The expected rate of return on a risky asset can be thought of as composed of two terms. s The return on a riskfree security, like U. S. Treasury bills. s A risk premium to compensate investors for bearing risk. E(r) = rf + Risk x [Market Price of Risk]

The Capital Asset Pricing Model n n The tradeoff between risk and return for the market portfolio is: This gives us the following relationship:

The Capital Asset Pricing Model n n This can be written explicitly as follows: This implies that for each security j the following relationship must hold:

The Capital Asset Pricing Model n Using the definition of l, we have the relationship between risk and expected return for individual stocks and portfolios. This is called the Security Market Line. where

The CAPM Expected Return E [ rm ] M Security Market Line rf 1 Beta

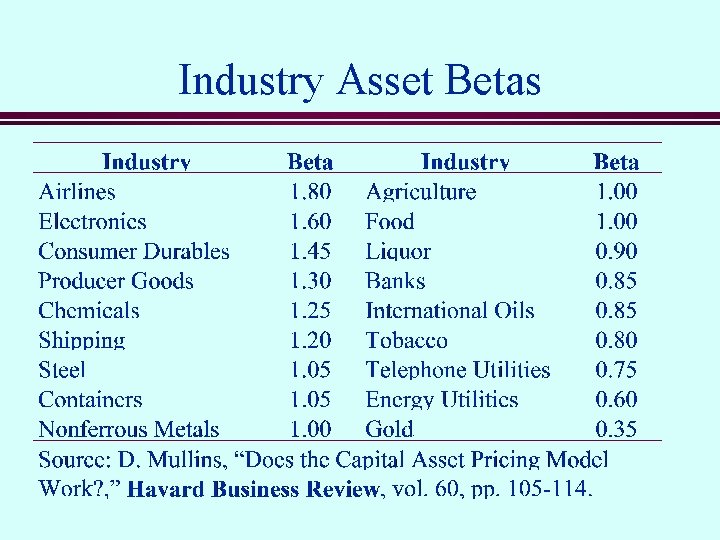
The Capital Asset Pricing Model n n n The appropriate measure of risk for an individual stock is its beta. Beta measures the stock’s sensitivity to market risk factors. The higher the beta, the more sensitive the stock is to market movements. The average stock has a beta of 1. 0. Portfolio betas are weighted averages of the betas for the individual stocks in the portfolio. The market price of risk is [E(r. M)-rf].

The CML and SML

Review of Intuition for the CAPM

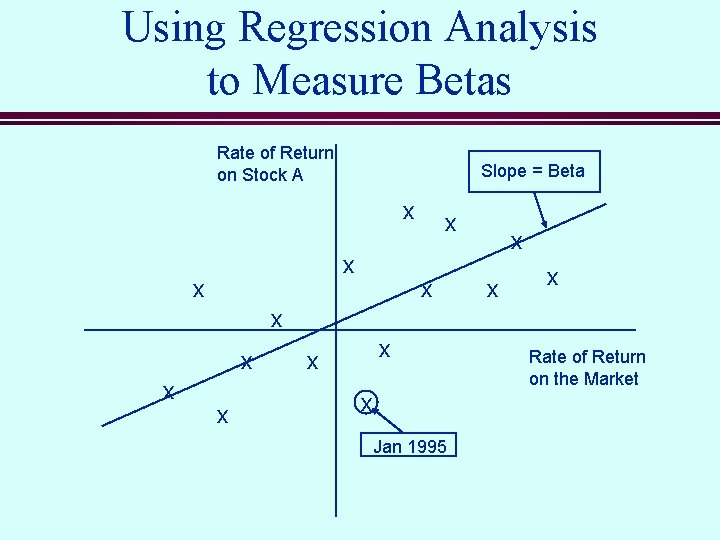
Using Regression Analysis to Measure Betas Rate of Return on Stock A Slope = Beta x x x x Jan 1995 Rate of Return on the Market

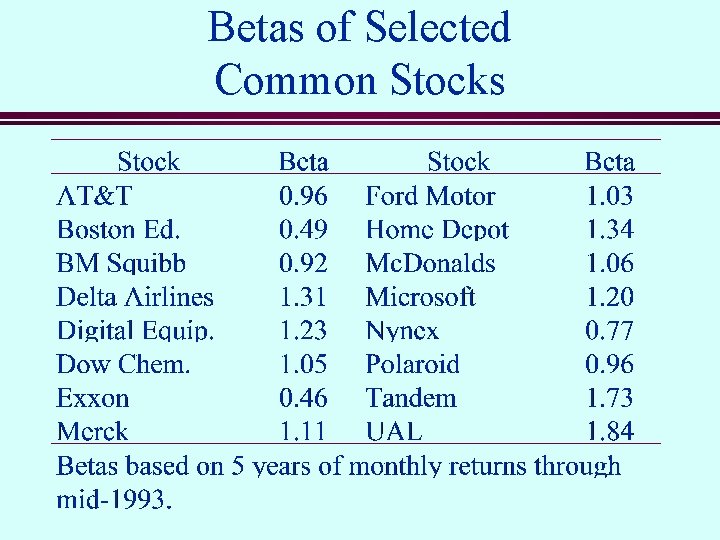
Betas of Selected Common Stocks

Estimating the Expected Rate of Return on Equity n n The SML gives us a way to estimate the expected (or required) rate of return on equity. We need estimates of three things: s Riskfree interest rate, rf. s Market price of risk, [E(r. M)-rf]. s Beta for the stock, bj.

Estimating the Expected Rate of Return on Equity n n n The riskfree rate can be estimated by the current yield on one-year Treasury bills. As of early 1996, one-year Treasury bills were yielding about 5. 0%. The market price of risk can be estimated by looking at the historical difference between the return on stocks and the return on Treasury bills. Earlier we saw this difference has averaged about 8. 6% since 1926. The betas are estimated by regression analysis.

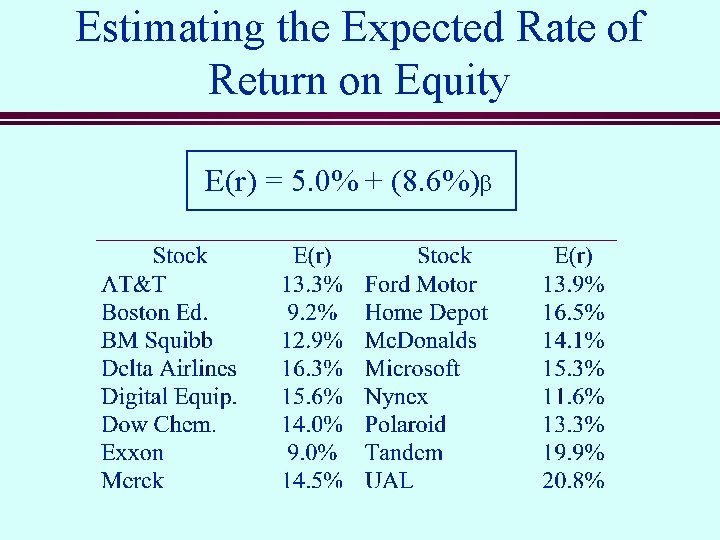
Estimating the Expected Rate of Return on Equity E(r) = 5. 0% + (8. 6%)b

Example of Portfolio Betas and Expected Returns n What is the beta and expected rate of return of an equally-weighted portfolio consisting of Exxon and Polaroid? Portfolio Beta n Expected Rate of Return n

Example of Portfolio Betas and Expected Returns n n How would you construct a portfolio with the same beta and expected return, but with the lowest possible standard deviation? Use the figure on the following page to locate the equally-weighted portfolio of Exxon and Polaroid. Also locate the minimum variance portfolio with the same expected return.

Graphical Illustration E(r) CML 13. 6% SML M M 11. 1% 5. 0% s. M s 0. 71 1. 0 b

Example n n n The S&P 500 Index has a standard deviation of about 12% per year. Gold mining stocks have a standard deviation of about 24% per year and a correlation with the S&P 500 of about r = 0. 15. If the yield on U. S. Treasury bills is 6% and the market risk premium is [E(r. M)-rf] = 7. 0%, what is the expected rate of return on gold mining stocks?

Example n n The beta for gold mining stocks is calculated as follows: The expected rate of return on gold mining stocks is:

Example n n Question: What portfolio has the same expected return as gold mining stocks, but the lowest possible standard deviation? Answer: A portfolio consisting of 70% invested in U. S. Treasury bills and 30% invested in the S&P 500 Index.

Using the CAPM for Project Evaluation n Suppose Microsoft is considering an expansion of its current operations. The expansion will cost $100 million today and is expected to generate a net cash flow of $25 million per year for the next 20 years. s What is the appropriate risk-adjusted discount rate for the expansion project? s What is the NPV of Microsoft’s investment project?

Microsoft’s Expansion Project n n The risk-adjusted discount rate for the project, rp, can be estimated by using Microsoft’s beta and the CAPM. Thus, the NPV of the project is:

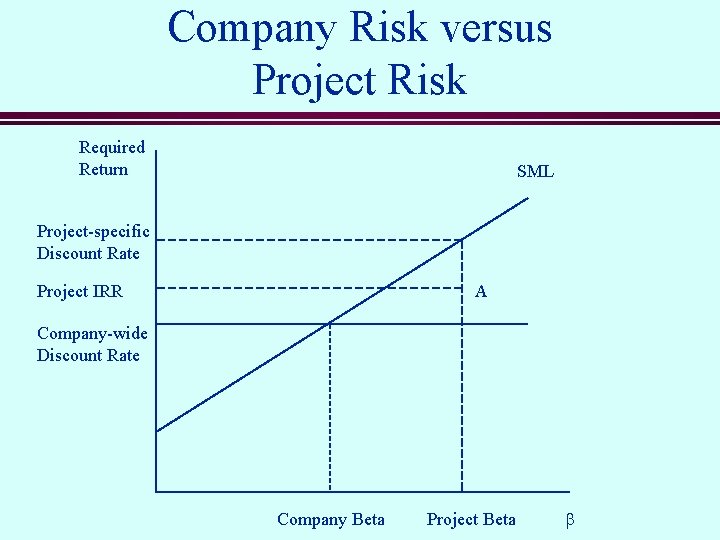
Company Risk Versus Project Risk n n n The company-wide discount rate is the appropriate discount rate for evaluating investment projects that have the same risk as the firm as a whole. For investment projects that have different risk from the firm’s existing assets, the companywide discount rate is not the appropriate discount rate. In these cases, we must rely on industry betas for estimates of project risk.

Company Risk versus Project Risk n Suppose Microsoft is considering investing in the development of a new airline. s What is the risk of this investment? s What is the appropriate risk-adjusted discount rate for evaluating the project? s Suppose the project offers a 17% rate of return. Is the investment a good one for Microsoft?

Industry Asset Betas

Company Risk versus Project Risk n n The project risk is closer to the risk of other airlines than it is to the risk of Microsoft’s software business. The appropriate risk-adjusted discount rate for the project depends upon the risk of the project. If the average asset beta for airlines is 1. 8, then the project’s cost of capital is:

Company Risk versus Project Risk Required Return SML Project-specific Discount Rate Project IRR A Company-wide Discount Rate Company Beta Project Beta b

Summary n n n The risk of an investment project is given by the project’s beta. The Security Market Line provides an estimate of an appropriate discount rate for the project based upon the project’s beta. This discount rate is used when computing the project’s net present value.