Class 7 Hidden Markov Models Sequence Models u

Class 7: Hidden Markov Models .

Sequence Models u So far we examined several probabilistic models l sequence models u These model, however, assumed that positions are independent l This means that the order of elements in the sequence did not play a role u In this class we learn about probabilistic models of sequences

Probability of Sequences an alphabet u Let X 1, …, Xn be a sequence of random variables over u Fix u We want to model P(X 1, …, Xn)

Markov Chains Assumption: u Xi+1 is independent of the past once we know Xi This allows us to write:

Markov Chains (cont) Assumption: u P(Xi+1|Xi) is the same for all i Notation P(Xi+1=b |Xi=a ) = Aab specifying the matrix A and initial probabilities, we define P(X 1, …, Xn) u To avoid the special case of P(X 1), we can use a special start state, and denote P(X 1 = a) = Asa u By

Example: Cp. G islands u In human genome, Cp. G dinucleotides are relatively rare l Cp. G pairs undergo a process called methylation that modifies the C nucleotide l A methylated C can (with relatively high chance) mutate to a T u Promotor regions are Cp. G rich l l These regions are not methylated, and thus mutate less often These are called Cp. G islands

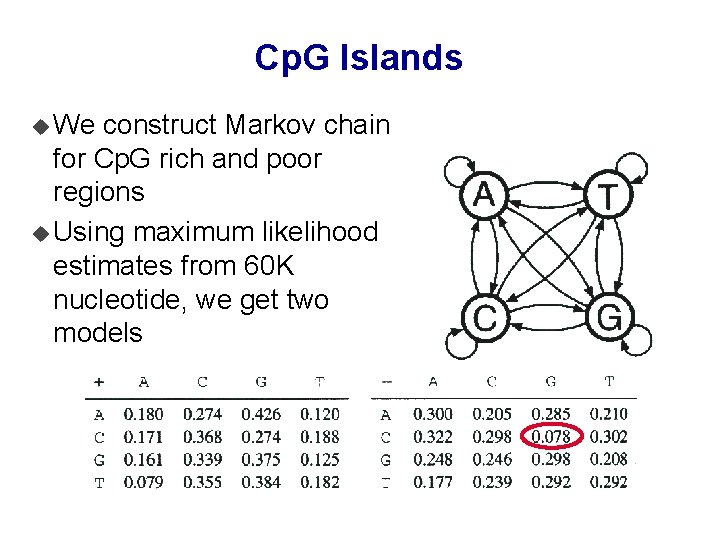
Cp. G Islands u We construct Markov chain for Cp. G rich and poor regions u Using maximum likelihood estimates from 60 K nucleotide, we get two models

Ratio Test for Cp. G islands a sequence X 1, …, Xn we compute the likelihood ratio u Given

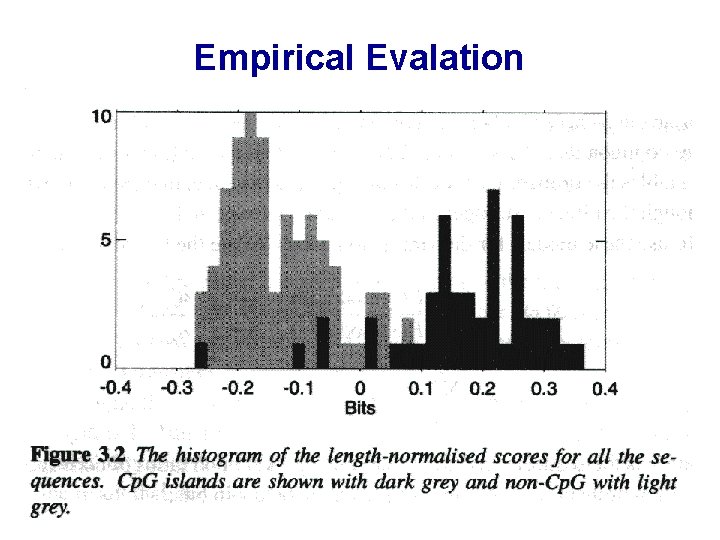
Empirical Evalation

Finding Cp. G islands Simple Minded approach: u Pick a window of size N (N = 100, for example) u Compute log-ratio for the sequence in the window, and classify based on that Problems: u How do we select N? u What do we do when the window intersects the boundary of a Cp. G island?

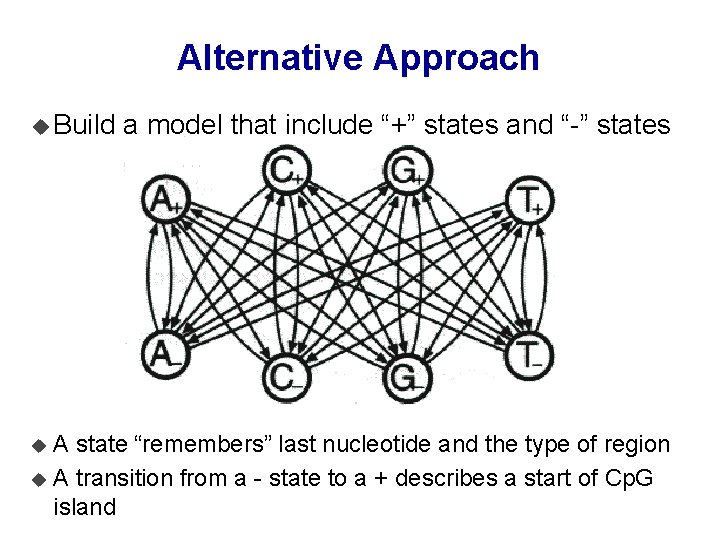
Alternative Approach u Build a model that include “+” states and “-” states A state “remembers” last nucleotide and the type of region u A transition from a - state to a + describes a start of Cp. G island u

Hidden Markov Models Two components: u A Markov chain of hidden states H 1, …, Hn with L values l P(Hi+1=k |Hi=l ) = Alk X 1, …, Xn Assumption: Xi depends only on hidden state Hi P(Xi=a |Hi=k ) = Bka u Observations l l

Semantics

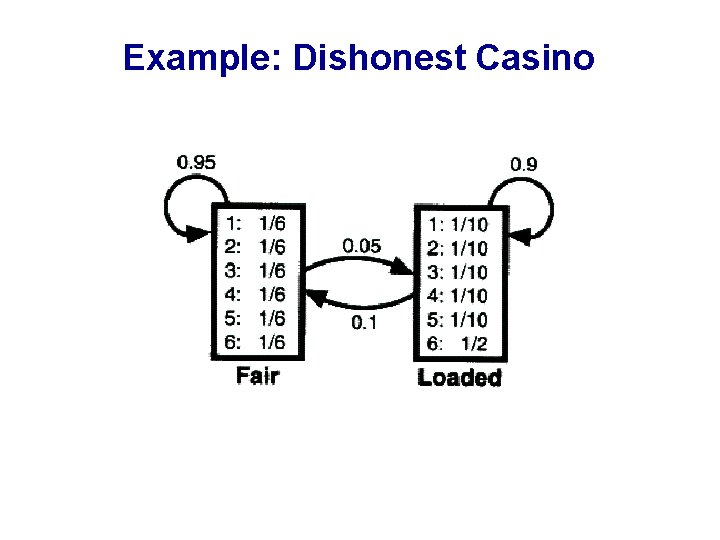
Example: Dishonest Casino

Computing Most Probable Sequence Given: x 1, …, xn Output: h*1, …, h*n such that

Idea: u If we know the value of hi, then the most probable sequence on i+1, …, n does not depend on observations before time i Vi(l) be the probability of the best sequence h 1, …, hi such that hi = l u Let

Dynamic Programming Rule u so

Viterbi Algorithm V 0(0) = 1, V 0(l) = 0 for l > 0 u for i = 1, …, n l for l = 1, …, L H set u Set h*n = argmaxl Vn(l) u for i = n-1, …, 1 l set h*i = Pi+1(h*i+1) u Let

Viterbi Algorithm – Example

Computing Probabilities Given: x 1, …, xn Output: P(x 1, …, xn ) How do we sum exponential number of hidden sequences?

Forward Algorithm u Perform dynamic programming on sequences u Let fi(l) = P(x 1, …, xi, Hi=l) u Recursion rule: u Conclusion

Computing Posteriors u How do we compute P(Hi | x 1, …, xn) ?

Backward Algorithm u Perform dynamic programming on sequences u Let bi(l) = P(xi+1, …, xn|Hi=l) u Recursion rule: u Conclusion

Computing Posteriors u How do we compute P(Hi | x 1, …, xn) ?

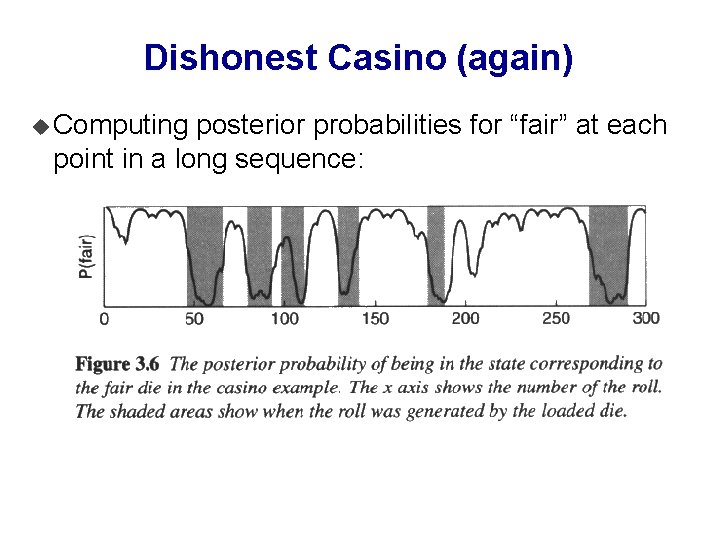
Dishonest Casino (again) u Computing posterior probabilities for “fair” at each point in a long sequence:

Learning Given a sequence x 1, …, xn, h 1, …, hn u How do we learn Akl and Bka ? u We want to find parameters that maximize the likelihood P(x 1, …, xn, h 1, …, hn) We simply count: u Nkl - number of times hi=k & hi+1=l u Nka - number of times hi=k & xi = a

Learning Given only sequence x 1, …, xn u How do we learn Akl and Bka ? u We want to find parameters that maximize the likelihood P(x 1, …, xn) Problem: u Counts are inaccessible since we do not observe hi

u If we have Akl and Bka we can compute

Expected Counts u We can compute expected number of times hi=k & hi+1=l u Similarly

Expectation Maximization (EM) u Choose Akl and Bka E-step: u Compute expected counts E[Nkl], E[Nka] M-Step: u Restimate: u Reiterate

EM - basic properties u P(x 1, …, xn: Akl, l u Bka) P(x 1, …, xn: A’kl, B’ka) Likelihood grows in each iteration If P(x 1, …, xn: Akl, Bka) = P(x 1, …, xn: A’kl, B’ka) then Akl, Bka is a stationary point of the likelihood l either a local maxima, minima, or saddle point

Complexity of E-step u Compute forward and backward messages l Time & Space complexity: O(n. L) u Accumulate expected counts l Time complexity O(n. L 2) l Space complexity O(L 2)

EM - problems Local Maxima: u Learning can get stuck in local maxima u Sensitive to initialization u Require some method for escaping such maxima Choosing L u We often do not know how many hidden values we should have or can learn