Class 4 Tues Sept 21 ExternalInternal Reliability Clarification

Class 4: Tues. , Sept. 21 • External/Internal Reliability Clarification • Regression Analysis Examples: – Appropriate Dating Ages – Father’s and son’s heights • Variability of Y given X in the Simple Linear Regression Model

Reliability • In general, a measurement is reliable if it gives consistent results. • My distinction between internal/external reliability of a measurement (e. g. , a test) was not very precise. Here’s a better categorization. • Four types of reliability for a measurement (degree of reliability can be measured by correlation): 1. Inter-observer: Different measurements of the same object/information give consistent results (e. g. , two psychiatrists rate the behavior of a patient similarly; two Olympic judges score a gymnastics contestant similarly).

Types of Reliability Continued 2. Test-retest: Measurements taken at two different times are similar (e. g. , a person’s pulse is similar for two different readings) 3. Parallel form: Two tests of different forms that supposedly test the same material give similar results (e. g. , a person’s SAT scores are similar for two forms of the test). 4. Split-half: If the items on a test are divided in half (e. g. , odd vs. even), the scores on the two halves are similar.

Examples of Reliability Example Type Correlation Pulse Test-Retest 0. 90 Bedtime on a Wed. SAT scores Test-Retest 0. 52 Parallel Form or Split Half (not clear) 0. 91

Regression Analysis • Provides a model for the mean of Y given X=X 0, E(Y|X=X 0) and the variability of Y given X=X 0. Useful for understanding the association between Y and X and for predicting Y based on X. • Simple linear regression model: – – – has a normal distribution with mean 0 and standard deviation

Example: What age is too young? • In U. S. culture, an older man dating a younger woman is not uncommon but when the age difference becomes too large, it may seem to some be unacceptable. • A survey was taken of ten people whom were each asked the minimum acceptable age for a woman to be dating a man of a certain age for a range of ages. • Y=minimum acceptable age of woman dating man of X years of age. X=age of man • What is the mean of people’s minimum acceptable for a woman to be dating a man of X years of age, i. e. , what is E(Y|X=X 0)?

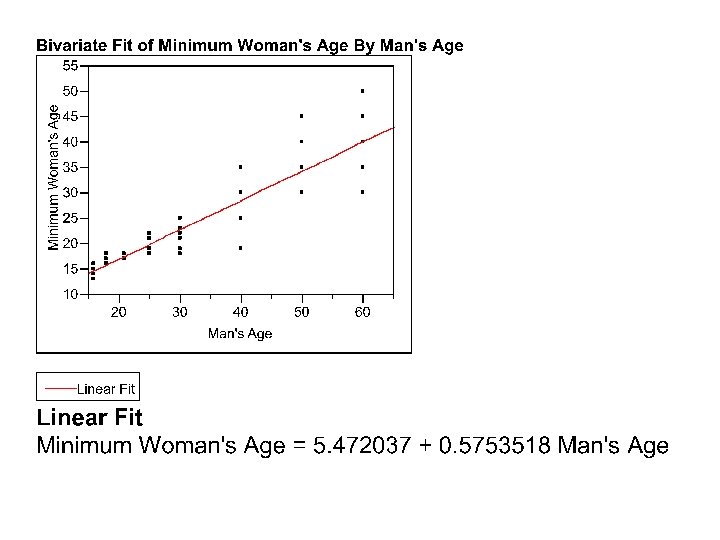
Linear Fit Minimum Woman's Age = 5. 472037 + 0. 5753518 Man's Age • Estimated Mean (among survey population) Minimum Acceptable Age for a Woman dating a man who is – – – 20 years old: 5. 47+0. 58*20 = 17. 07 30 years old: 5. 47+0. 58*30 = 22. 87 40 years old: 5. 47+0. 58*40 = 28. 67 50 years old: 5. 47+0. 58*50 =34. 47 60 years olds: 5. 47+0. 58*60=40. 27 70 years old: 5. 47+0. 58*70 = 46. 07

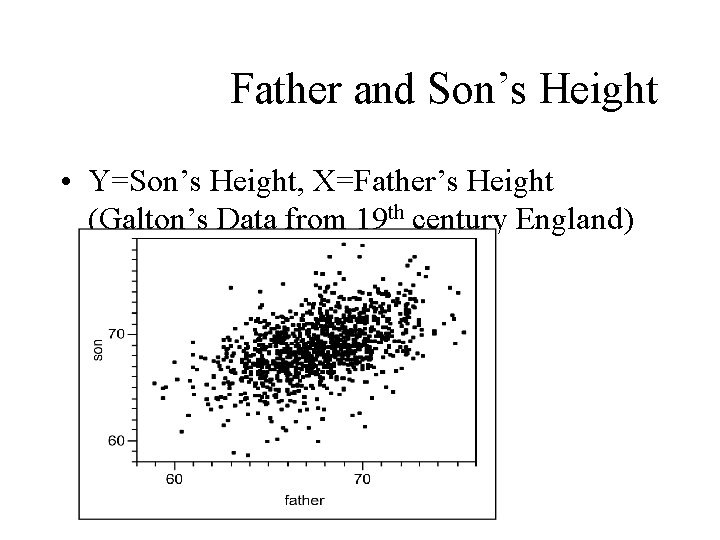
Father and Son’s Height • Y=Son’s Height, X=Father’s Height (Galton’s Data from 19 th century England)

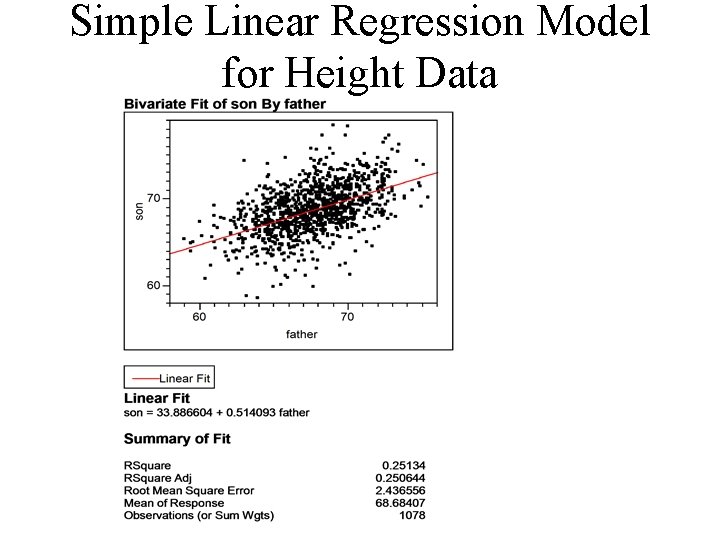
Simple Linear Regression Model for Height Data

• Estimated regression model: E(Son’s height | Father’s Height ) = 33. 89 + 0. 51 *Father’s height • Estimated slope = 0. 51. For each additional inch of father’s height, the mean son’s height increases by 0. 51 inches. • Predicted son’s heights: – Father’s height = 60 inches. Predicted son’s height = 33. 89 + 0. 51 * 60 = 64. 5 inches – Father’s height = 72 inches. Predicted son’s height = 33. 89 + 0. 51 * 72 = 70. 6 inches

Variability of Y given X • The simple linear regression model tells us more than the mean of Y given X=X 0, it tells us about the variability and distribution of Y given X=X 0. • Simple linear regression model: – has a normal distribution with mean 0 and standard deviation (SD) – The subpopulation of Y with corresponding X=X 0 has a normal distribution with mean and SD –

Residuals and Estimating • Estimating – Use least squares to estimate the slope and intercept of the simple linear regression model. Denote the slope estimates by and the intercept estimate by – Predicted value of Yi for observation i based on Xi and regression model estimate: – Residual for observation i: Prediction error of using least squares line to predict Yi for observation i – Root mean square error = (approximately) standard deviation of residuals. Root mean square error is an estimate of • For father-son height data, root mean square error = 2. 4. This means that, according to the simple linear regression model, a son whose father is 72 inches has a mean height of 33. 89 +. 51*72 = 70. 6 inches with a standard deviation of 2. 4 inches.

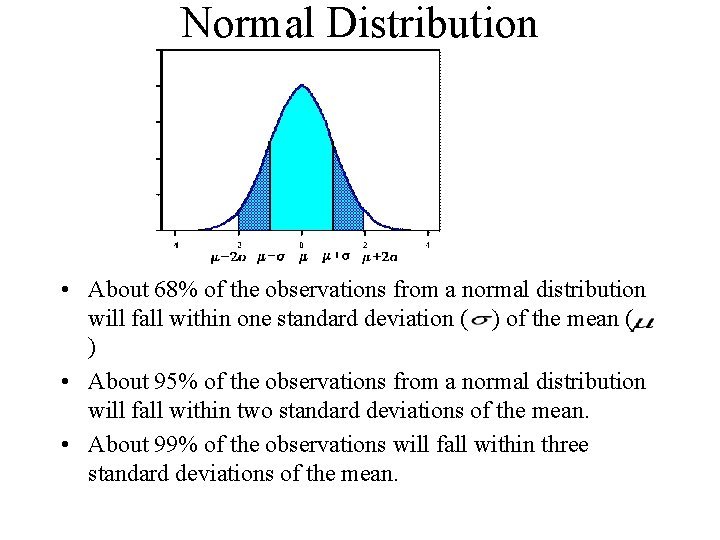
Normal Distribution • About 68% of the observations from a normal distribution will fall within one standard deviation ( ) of the mean ( ) • About 95% of the observations from a normal distribution will fall within two standard deviations of the mean. • About 99% of the observations will fall within three standard deviations of the mean.

Variability of Y given X • According to the estimated regression model, the distribution of heights for sons whose father are 72 inches is a normal distribution with a mean of 70. 6 inches and a standard deviation of 2. 4 inches. • If a son’s father’s height is 72 inches, – 68% of the time the son’s height will be between inches – 95% of the time, the son’s height will be between inches 99% of the time, the son’s height will be between inches.

Summary • Regression model provides information about both the mean of Y given X and the variability of Y given X. • For the simple linear regression model, the standard deviation of Y given X is estimated by the root mean square error. • For the simple linear regression model, approximately 68% of the time, Y given X will be within one root mean square error of the estimated mean of Y given X ( ), approximately 95% of the time, Y given X will be within two root mean square errors of the mean of Y given X.