Class 33 Making Recursion M C Escher Ascending















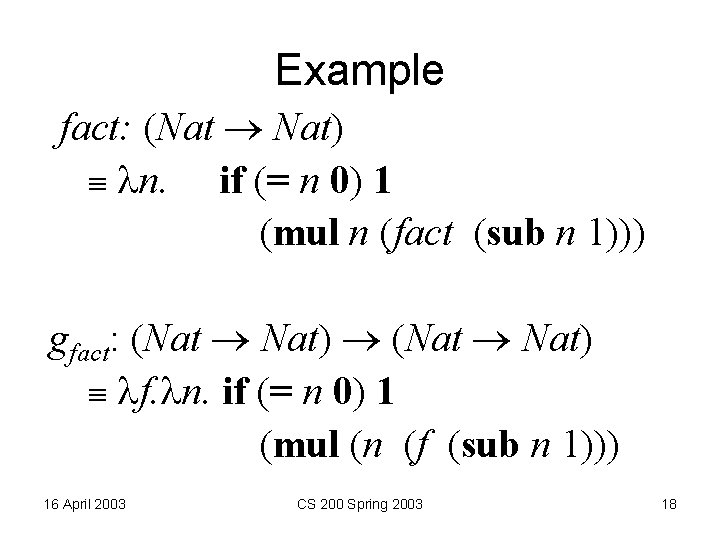















- Slides: 34

Class 33: Making Recursion M. C. Escher, Ascending and Descending also known as f. (( x. f (xx)) CS 200: Computer Science David Evans University of Virginia 16 April 2003 CS 200 Spring 2003 http: //www. cs. virginia. edu/evans Computer Science

Menu • Recap: Proving Lambda Calculus is Universal • How to make recursive definitions without define • Fixed points 16 April 2003 CS 200 Spring 2003 2

Lambda Calculus Review term : : = variable |term | (term)| variable. term Parens are just for grouping, not like in Scheme -reduction (renaming) y. M v. (M [y v]) where v does not occur in M. -reduction (substitution) ( x. M)N M [ x N ] ( f. (( x. f (xx)))) ( z. z) 16 April 2003 CS 200 Spring 2003 3

Universal Language • Is Lambda Calculus a universal language? – Can we compute any computable algorithm using Lambda Calculus? • To prove it isn’t: – Find some Turing Machine that cannot be simulated with Lambda Calculus • To prove it is: – Show you can simulate every Turing Machine using Lambda Calculus 16 April 2003 CS 200 Spring 2003 4

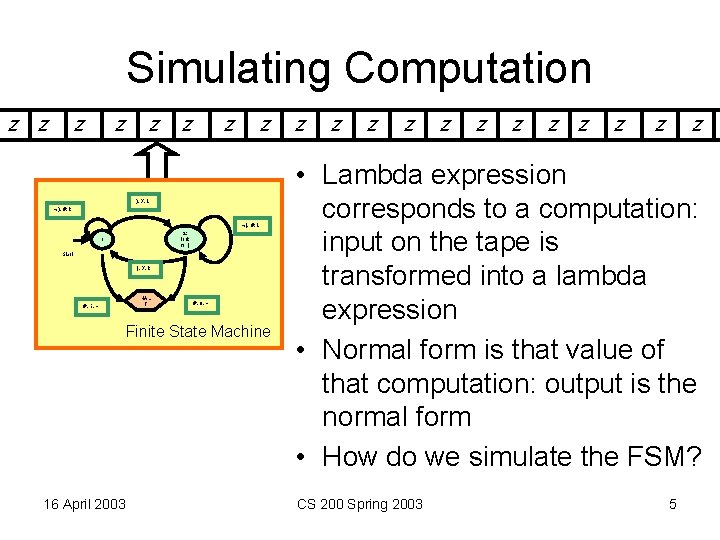
Simulating Computation z z z z ), X, L ), #, R (, #, L 2: look for ( 1 Start (, X, R #, 1, - HAL T #, 0, - Finite State Machine 16 April 2003 z z z • Lambda expression corresponds to a computation: input on the tape is transformed into a lambda expression • Normal form is that value of that computation: output is the normal form • How do we simulate the FSM? CS 200 Spring 2003 5

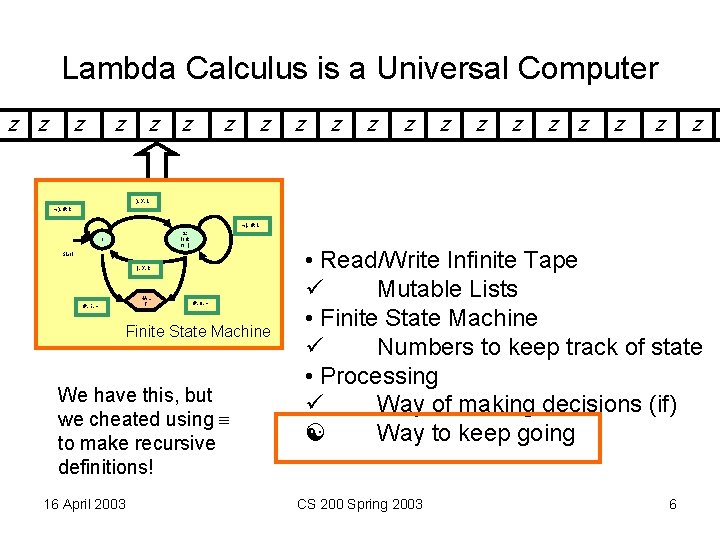
Lambda Calculus is a Universal Computer z z z z z ), X, L ), #, R (, #, L 2: look for ( 1 Start (, X, R #, 1, - HAL T #, 0, - Finite State Machine We have this, but we cheated using to make recursive definitions! 16 April 2003 • Read/Write Infinite Tape ü Mutable Lists • Finite State Machine ü Numbers to keep track of state • Processing ü Way of making decisions (if) [ Way to keep going CS 200 Spring 2003 6

Alyssa P. Hacker’s Answer ( f. (( x. f (xx)))) ( z. z) ( x. ( z. z)(xx)) ( z. z) ( x. ( z. z)(xx)) ( x. ( z. z)(xx)) . . . 16 April 2003 CS 200 Spring 2003 7

Recursive Definitions Which of these make you uncomfortable? x=1+x x=4–x x=9/x x=x x = 1 / (16 x 3) 16 April 2003 No solutions over integers 1 integer solution, x = 2 2 integer solutions, x = 3, x = -3 Infinitely many integer solutions No integer solutions, two rational solutions (1/2 and – 1/2), four complex solutions (1/2, -1/2, i/2, -i/2) CS 200 Spring 2003 8

Equations Functions x=4–x f x. sub 4 x Find an x such that (f x) = x. Same as solve for x. sub x. y. if (zero? y) x (sub (pred x) (pred y)) 16 April 2003 CS 200 Spring 2003 9

What’s a function? f x. sub 4 x f: Nat { <0, 4>, <1, 3>, <2, 2>, <3, 1>, <4, 0>, <5, ? ? ? >, . . . } 16 April 2003 CS 200 Spring 2003 10

Domains • Set: unordered collection of values Nat = { 0, 2, 1, 4, 3, 6, 5, 8, 7, . . . } • Domains: like a set, but has structure Nat = { 0, 1, 2, 3, 4, 5, 6, 7, 8, . . . } where 0 is the least element, and there is an order of the elements. 16 April 2003 CS 200 Spring 2003 11

Making Domains • Primitive domains can be combined to make new domains • Product domain: D 1 x D 2 – Pairs of values Nat x Nat = { (tuple. Nat, Nat 0 0), (tuple. Nat, Nat 0 1), (tuple. Nat, Nat 1 0), (tuple. Nat, Nat 1 1), (tuple. Nat, Nat 0 2), . . . } 16 April 2003 CS 200 Spring 2003 12

Functions • A set of input-output pairs – The inputs (Di) and outputs (Do) are elements of a domain • The function is an element of the domain Di Do. • It is a (completely defined) function if and only if for every element d Di, the set of input-output pairs has one member whose first member matches d. 16 April 2003 CS 200 Spring 2003 13

Functions? f: Nat z. sub. Nat 4 z Not a function since there is no value in output domain for z > 4. f: Nat Int z. sub. Nat Int 4 z f: Nat z. add. Nat z 1 16 April 2003 CS 200 Spring 2003 14

Functions f: (Nat Nat) n. add 1 ( f n)) No solutions (over natural numbers) – would require x = 1 + x. f: (Nat Nat) n. f (add 1 n)) = x. 3 { <0, 3>, <1, 3>, <2, 3>, . . . } Infinitely many solutions – e. g. , f(x) 16 April 2003 CS 200 Spring 2003 15

Fixed Points • A fixed point of a function f: (D is an element d D such that D) (f d) = d. • Examples: f: Nat Int z. sub 4 z f: Nat z. mul 2 z f: Nat z. z 16 April 2003 CS 200 Spring 2003 2 0 infinitely many 16

Generating Functions • Any recursive definition can be encoded with a (non-recursive) generating function f: (Nat Nat) n. (add 1 ( f n)) g: (Nat Nat) f. n. (add 1 ( f n)) • Solution to a recursive definition is a fixed point of its associated generating function 16 April 2003 CS 200 Spring 2003 17
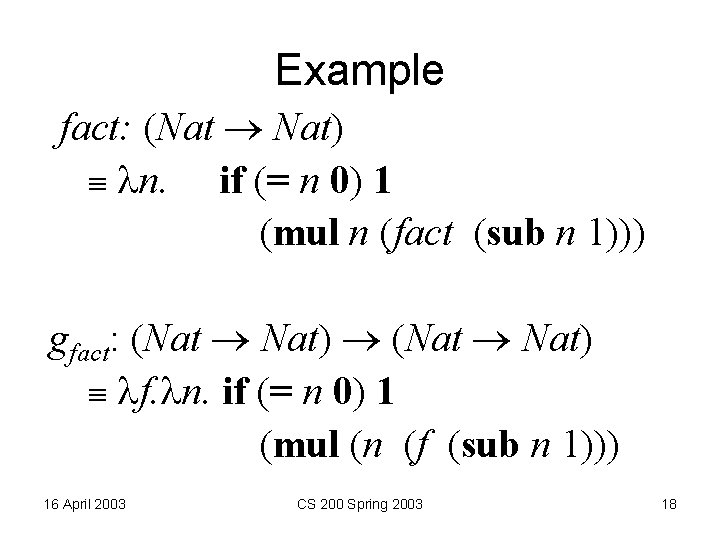
Example fact: (Nat Nat) n. if (= n 0) 1 (mul n (fact (sub n 1))) gfact: (Nat Nat) f. n. if (= n 0) 1 (mul (n (f (sub n 1))) 16 April 2003 CS 200 Spring 2003 18

gfact I gfact: (Nat Nat) f. n. if (= n 0) 1 (mul (n (f (sub n 1))) gfact ( z. z) n. if (= n 0) 1 (mul (n (( z. z) (sub n 1))) What is (gfact I) 5? 16 April 2003 CS 200 Spring 2003 19

gfact: (Nat Nat) f. n. if (= n 0) 1 (mul (n (f (sub n 1))) fact : (Nat Nat) n. if (= n 0) 1 (mul (n (fact (sub n 1))) gfact n. if (= n 0) 1 (mul n (fact (sub n 1))) fact is a fixed point of gfact 16 April 2003 CS 200 Spring 2003 20

Unsettling Questions • Is the factorial function the only fixed point of gfact? • Given an arbitrary function, how does one find a fixed point? • If there is more than one fixed point, how do you know which is the right one? 16 April 2003 CS 200 Spring 2003 21

Iterative Fixed Point Technique To find a fixed point of g: D D • Start with some element d D • Calculate g(d), g(g(d)), g(g(g(d))), . . . until you get g(g(v)) = v then v is a fixed point. 16 April 2003 CS 200 Spring 2003 22

Where to start? • If you start with D you get the least fixed point (which is the “best” one) • (pronounced “bottom”) is the element of D such that for any element d D, d. • means “has less information than” or “is weaker than” • Not all domains have a . 16 April 2003 CS 200 Spring 2003 23

Pointed Partial Order • A partial order (D, ) is pointed if it has a bottom element u D such that u d for all elements d D. 0 • Bottom of (Nat, <=)? • Bottom of (Nat, =)? Not a pointed partial order • Bottom of (Int, <=)? Not a pointed partial order {} • Bottom of ({Nat}, <=)? 16 April 2003 CS 200 Spring 2003 24

Getting to the of things • Think of bottom as the element with the least information, or the “worst” possible approximation. • Bottom of Nat is a function that is undefined for all inputs. That is, the function with the graph {}. • To find the least fixed point in a function domain, start with the function whose graph is {} and iterate. 16 April 2003 CS 200 Spring 2003 25

Least Fixed Point of gfact: (Nat Nat) f. n. if (= n 0) 1 mul n ( f (sub n 1))) gfactn (function with graph {}) = fact as n approaches infinity. 16 April 2003 CS 200 Spring 2003 26

Fixed Point Theorem Do all -calculus terms have a fixed point? 16 April 2003 CS 200 Spring 2003 27

Fixed Point Theorem • F , X such that FX = X • Proof: Let W = x. F(xx) and X = WW = ( x. F(xx))W F (WW) = FX 16 April 2003 CS 200 Spring 2003 28

Why of Y? • Y is f. WW: Y f. ( x. f (xx)) • Y calculates a fixed point of any lambda term! • Hence: we don’t need define to do recursion! – Works in Scheme too - check the “lecture” from the Adventure Game 16 April 2003 CS 200 Spring 2003 29

Fixed Point The fixed point of our Turing Machine simulator on some input is the result of running the TM on that input. If there is no fixed point, the TM doesn’t halt! fixed-point TM input result of running TM on input 16 April 2003 CS 200 Spring 2003 30

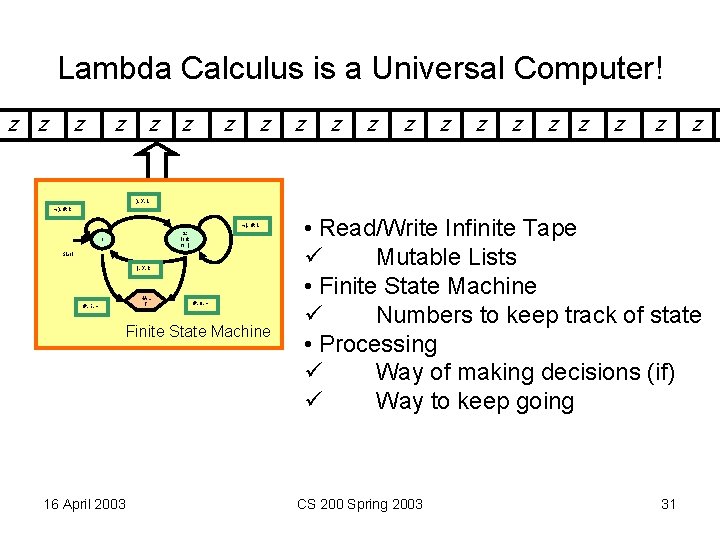
Lambda Calculus is a Universal Computer! z z z z z ), X, L ), #, R (, #, L 2: look for ( 1 Start (, X, R #, 1, - HAL T #, 0, - Finite State Machine 16 April 2003 • Read/Write Infinite Tape ü Mutable Lists • Finite State Machine ü Numbers to keep track of state • Processing ü Way of making decisions (if) ü Way to keep going CS 200 Spring 2003 31

Mystery Function (Teaser) p xy. pca ( x. x xy. x) x) y (p (( x. x xy. y) x) ( x. z. z ( xy. y) y) m xy. pca ( x. x xy. x) x) x. x (p y (m (( x. x xy. y) x) y)) f x. pca (( x. x xy. x) x) ( z. z ( xy. y) ( x. x)) (m x (f (( x. x xy. y) x))) 16 April 2003 CS 200 Spring 2003 32

QED • Lambda calculus is a Universal Programming language • All you need is beta-reduction and you can compute anything • Integers, booleans, if, while, +, *, =, <, classes, define, inheritance, etc. are for wimps! Real programmers only use and beta-reduction. 16 April 2003 CS 200 Spring 2003 33

Charge • Friday: chance to ask questions before Exam 2 is handed out – Email questions before if you want to make sure they are covered – Today’s lecture is not covered by Exam 2 • Office hours this week: – Wednesday, after class - 3: 45 – Thursday 10 am-10: 45 am; 4 -5 pm. 16 April 2003 CS 200 Spring 2003 34