Class 26 Rotation Chapter 10 Monday October 25

Class 26 - Rotation Chapter 10 - Monday October 25 th • Review Kinetic energy, moment of inertia, parallel axis theorem • Newton's second law for rotation • Work, power and rotational kinetic energy • Sample problems Reading: pages 241 thru 263 (chapter 10) in HRW Read and understand the sample problems Assigned problems from chapter 10 (due Sunday October 31 st at 11 pm): 2, 10, 28, 30, 36, 44, 48, 54, 58, 64, 78, 124
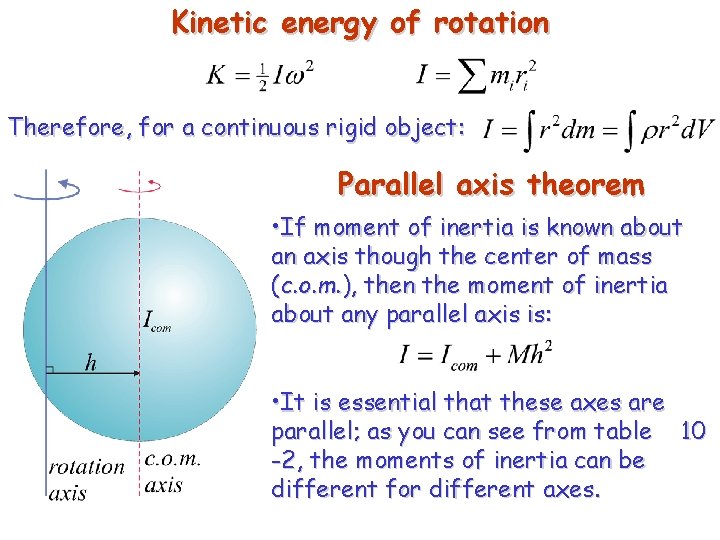
Kinetic energy of rotation Therefore, for a continuous rigid object: Parallel axis theorem • If moment of inertia is known about an axis though the center of mass (c. o. m. ), then the moment of inertia about any parallel axis is: • It is essential that these axes are parallel; as you can see from table 10 -2, the moments of inertia can be different for different axes.
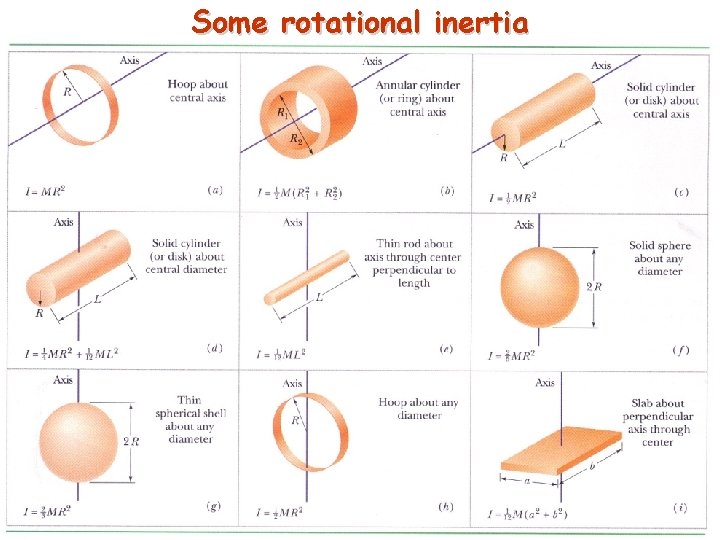
Some rotational inertia

Torque • The ability to rotate an object about an axis depends not only on the force you apply, but also where and in what direction you apply the force. • In particular, the further away from the axis that you push, the easier it is to rotate the object. • We define a quantity called torque, t: • The SI unit for torque is N. m, which is the same as that for work (joule). • However, torque and work are quite different and should not be confused.
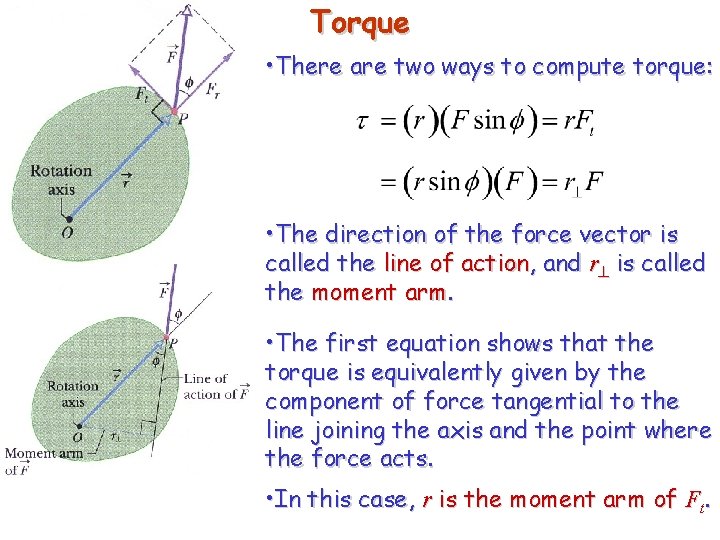
Torque • There are two ways to compute torque: • The direction of the force vector is called the line of action, and r is called the moment arm. • The first equation shows that the torque is equivalently given by the component of force tangential to the line joining the axis and the point where the force acts. • In this case, r is the moment arm of Ft.
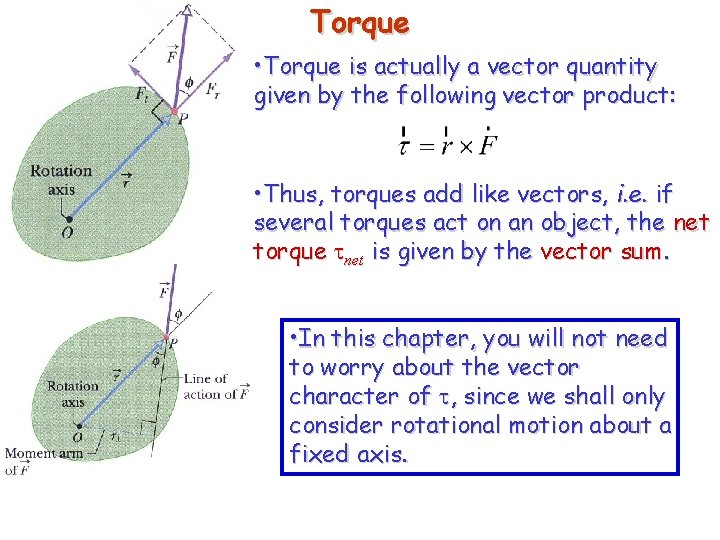
Torque • Torque is actually a vector quantity given by the following vector product: • Thus, torques add like vectors, i. e. if several torques act on an object, the net torque tnet is given by the vector sum. • In this chapter, you will not need to worry about the vector character of t, since we shall only consider rotational motion about a fixed axis.

Newton's second law for rotation • We can relate Ft to the tangential acceleration using Newton's second law: • The torque t is then given by: Substituting ar for at. For a rigid body which is free to rotate about a fixed axis, Fr cannot affect the motion.

Work and rotational kinetic energy (Work-kinetic energy theorem) • By now, you should be noticing a pattern in the connections between linear and angular equations: x q; v w; a a; m I; F t, etc. . • Then, kinetic energy is calculated by substituting the linear variables by their corresponding angular variables. • We can do the same for work and power. (Work, rotation about a fixed axis) (Work at constant torque) (Power, rotation about a fixed axis)

Summarizing relations for translational and rotational motion • Note: work obtained by multiplying torque by an angle - a dimensionless quantity. Thus, torque and work have the same dimensions, but you see that they are quite different.
- Slides: 9