Class 2 Probability Theory Discrete Random Variables Expectations

Introduction to Probability • A probability is a number between 0 and 1 inclusive that measures the likelihood of the occurrence of an event. • Given an event, E, we will write the probability of E as P{E} or Pr{E}. • One early notion of probability came from the observation of relative frequencies of events that occurred from replication of some process (like rolling dice).

Outcome Spaces • Another perspective on probabilities comes from the notion of an outcome space. • Consider all possible outcomes (events) of an experiment. • Example: Consider the experiment performed by throwing a die and looking at the top surface. What is the outcome space? • What is the P{3}? P{odd number}?

Applying Set Concepts to Compute Probabilities • The union of events A and B (A B) are all of the outcomes that make A or B occur. • The intersection of events A and B (A B) are all of the outcomes that make A and B occur at the same time. • For the die example, let A: {throw less than or equal to 4} and B: {even number}.

Example Computation (cont. ) • What is P{A}? • P{B}? • P{A B}? It turns out that P{A B} = P{A} + P{B} - P{A B}.

Conditional Probability • Consider all families with two children. What does the outcome space look like? • Select such a family. Let A: {the family has at least one male child} and B: {the family has exactly two male children}. • What is P{A}? P{B}? P{A B}?

Conditional Probability (cont. ) • Now suppose that A has occurred. What had to happen? • Are these outcomes equally likely? • We will write {B|A} to indicate the event B given that A has occurred. What is P{B|A}? It turns out that P{B|A} = P{A B}/P{A}

Special Relationships • Two events, A and B, are said to be mutually exclusive if and only if P{A B}=0. In this case, P{A B} = P{A} + P{B}. • Two events, A and B, are said to be independent if and only if P{A|B} = P{A}. In this case, P{A B} = P{A}P{B}. • An event B is said to be the complement of A if it always happens exactly when A does not happen. In this case P{B} = 1 - P{A}.

Contingency Tables • A contingency table is a cross classification of data displayed in a tabular form. • In a decision making context (such as a marketing study), the decision maker might treat the relative frequencies found in the table as if they were probabilities. • Consider the attached example where a department store has analyzed 10, 000 sales to better understand the relationship between type of purchase (cash or credit) and merchandise.

Contingency Tables A B: B C: A|B:

Contingency Tables P{A B} P{B C}

Contingency Tables P{A|B}

Random Variables • A random variable is a model of a population. When we discuss random variables, we are simply talking about populations. • To illustrate how a population can be modeled, consider the experiment where we flip a coin three times.

Populations and RV’s Count the number of heads that you see. 2 1 1 2 0 2 1 0 3 2 2 1 3 2 1 1 How large is the population? 0 3 0 1 1 0 2 2 3

Probability Distributions • The probability distribution of X is just a listing (or graph) of the values of X along with the probability that X assumes that value. X 0 1 2 3 p(x) 1/8 3/8 1/8

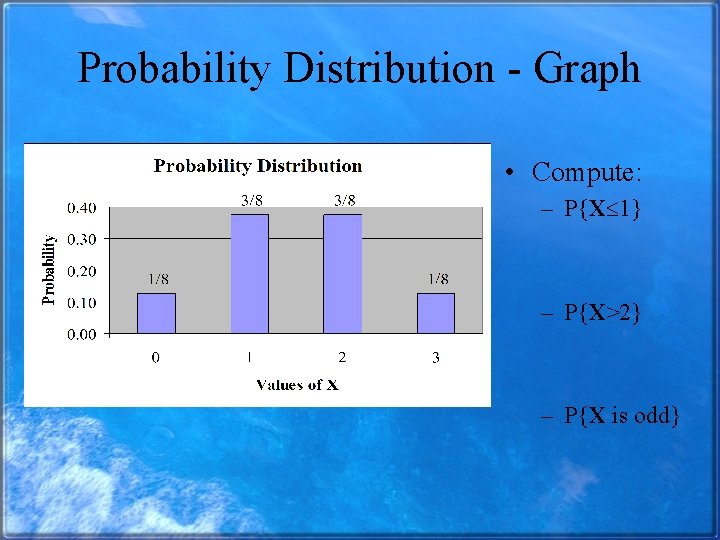
Probability Distribution - Graph • Compute: – P{X 1} – P{X>2} – P{X is odd}

Random Variables • Remember: – A probability distribution is a list of the values and probabilities that a random variable assumes. – These values can be thought of as the values in a population, and the probabilities as the proportion of the population that a specific value makes up. • Random variables can be classified as being discrete or continuous. Continuous random variables assume values along a continuum.

Discrete Random Variables • Our example of counting the number of heads in three coin flips was an example of a discrete random variable. Why? • An example of a continuous random variable is W = the amount of gasoline in your car. • We will return to continuous random variables shortly.

The Mean of a Random Variable • Since a random variable is just describing a population, it has a mean (average) value. What should we call this average?

Variance of a Random Variable • The variance provided a measure of dispersion of the values in the data, the average squared distance from .