Class 15 Recursive sorting methods r Processing arrays

Class 15 - Recursive sorting methods r Processing arrays by recursion r Divide-and-conquer algorithm r Quicksort 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 1

Processing arrays by recursion r Follow usual principle: to define f(A), assume f(B) can be calculated for any array B smaller than A. r But, instead of actually passing in a smaller array, pass A together with arguments indicating which part of A to process. r Examples: void f (double[] A, int i, int j) { // process A[i]. . . A[j]. . . recursive call f(A, i+1, j). . . } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 2

Processing arrays by recursion (cont. ) void f (double[] A, int i, int j) { // process A[i]. . . A[j]. . . recursive call f(A, i, j-1). . . } void f (double[] A, int i) { // process A[i]. . . A[A. length-1]. . . recursive call f(A, i+1). . . } void f (double[] A, int i) { // process A[0]. . . A[i]. . . recursive call f(A, i-1). . . } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 3

Processing arrays by recursion (cont. ) r Base cases void f (double[] A, int i, int j) { // i = j - 1 -element subarray // i > j - 0 -element subarray void f (double[] A, int i) { // process A[i]. . . A[A. length-1] // i = A. length-1 - 1 -element // i = A. length - 0 -element 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 4

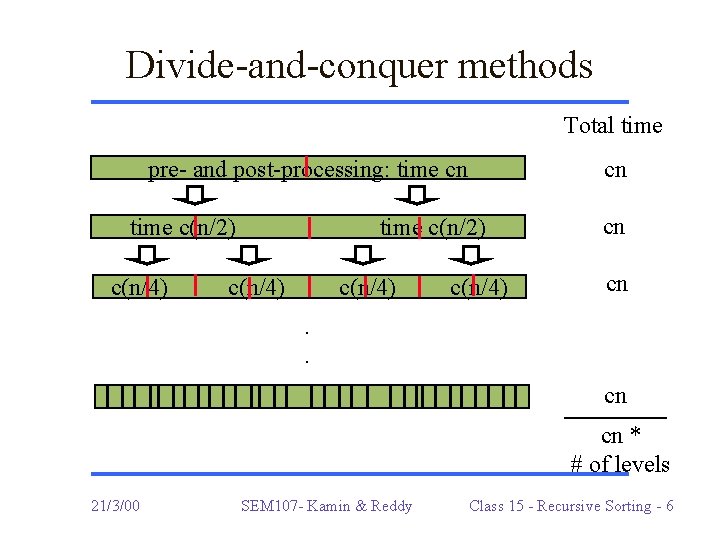
Divide-and-conquer methods r Greater efficiency sometimes obtained by dividing array in half, operating on each half recursively. void f (double[] A, int i, int j) { // process subarray A[i]. . . A[j]. . . process A[i]. . . A[j] in linear time. . . f(A, i, (i+j)/2); f(A, (i+j)/2+1, j); . . . process A[i]. . . A[j] in linear time. . . } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 5

Divide-and-conquer methods Total time pre- and post-processing: time cn time c(n/2) c(n/4). . . c(n/4) cn cn * # of levels 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 6

Divide-and-conquer methods for sorting r Consider subarrays of the form A[i]. . . A[j]. Assuming can sort arbitrary subarrays - in particular, A[i]. . . A[(i+j)/2] and A[(i+j)/2+1]. . . A[j] - how can we define divide-andconquer sorting method? r Two “obvious” methods: 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 7

Divide-and-conquer methods for sorting (cont. ) ¬ “Post-process”: To sort A[i]. . . A[j]: m Sort A[i]. . . A[(i+j)/2] m Sort A[(i+j)/2+1]. . . A[j] m “Merge” sorted halves 17 9 22 5 4 16 8 12 sort 5 9 17 22 4 8 12 16 merge 4 21/3/00 5 8 9 12 16 17 22 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 8

Divide-and-conquer methods for sorting (cont. ) “Pre-process”: To sort A[i]. . . A[j]: m Move smaller elements into left half and larger elements into right half (“partition”) m Sort A[i]. . . A[(i+j)/2] m Sort A[(i+j)/2+1]. . . A[j] 17 9 22 5 4 16 8 12 partition 4 9 8 5 17 16 22 12 4 5 8 9 12 16 17 22 sort 21/3/00 sort SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 9

Divide-and-conquer methods for sorting (cont. ) r Method 1 called merge sort m But need to write merge step r Method 2 called quicksort m But 21/3/00 need to write partition step SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 10

Quicksort “Pre-process”: To sort A[i]. . . A[j]: m Move smaller elements into left half and larger elements into right half (“partition”) m Sort A[i]. . . A[(i+j)/2] m Sort A[(i+j)/2+1]. . . A[j] 17 9 22 5 4 16 8 12 partition 4 9 8 5 17 16 22 12 4 5 8 9 12 16 17 22 sort 21/3/00 sort SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 11

Quicksort (cont. ) void quick. Sort (double[] A, int i, int j) { // sort A[i]. . . A[j] if (base case). . . handle base case. . . ; else { partition(A, i, j); int midpt = (i+j)/2; quick. Sort(A, i, midpt); quick. Sort(A, midpt+1, j); } } (N. B. this is the right idea, but it doesn’t work in this form. We’ll fix it in a little while. ) 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 12

Quicksort (cont. ) r Only question is how to partition. r Can divide problem into two subproblems: m locating the “median” element in A[i. . j], say it is A[m]. (This value is called the pivot. ) m moving smaller elements than A[m] to left, larger elements to right. void partition (double[] A, int i, int j) { int pivot. Loc = loc. Of. Median(A, i, j); swap(A, i, pivot. Loc); partition 1(A, i+1, j, A[i]); } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 13

partition 1, first version r partition 1(double[] A, int i, int j, - shuffle elements of A[i. . j] so that all elements less than pivot appear to the left of all elements greater than pivot. r If pivot is the median of the elements of A[i. . j], then this will split the subarray exactly in half, so that the “middle” will be (i+j)/2. double pivot) 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 14

partition 1, first version r Idea is simple: Suppose can partition A[i+1. . j] or A[i. . j-1] recursively. Two cases: m A[i] < x: Partition A[i+1. . j]. m A[i] > x: Swap A[i] and A[j], then partition A[i. . j-1] recursively. 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 15

partition 1, first version void partition 1 (double[] A, int i, int j, double pivot) { // Shuffle elements of A[i. . j] so that elements // < pivot appear to the left of elements > pivot if (A[i]<pivot) … … write this! } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 16

Finding the median r Next problem: find median of A[i. . j]. r Can easily do it in quadratic time, but how can it be done in linear time? 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 17

Guessing the median r Unfortunately, it can’t. Second best solution: guess the median and partition around the guess, hoping for the best. r Major point: Since we can’t be sure our guess will be correct, we don’t know where the “middle” will end up. Therefore, partition 1 needs to return an integer giving the location of the dividing line between small and large values. 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 18

Quicksort again r Without the ability to divide the array exactly in half, need to change structure of quicksort somewhat: void quick. Sort (double[] A, int i, int j) { int m; if (i < j) { m = partition(A, i, j); quick. Sort(A, i, m-1); quick. Sort(A, m+1, j); } } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 19

Quicksort again (cont. ) r Difference is that partition has to tell quicksort where it ended up splitting the array: int partition (double[] A, int i, int j) { // Guess median of A[i]. . . A[j], // and move other elements so that // A[i]. . . A[m-1] are all less than A[m] and // A[m+1]. . . A[j] are all greater than A[m] // m is returned to the caller swap(A, i, guess. Median. Location(A, i, j)); int m = partition 1(A, i+1, j, A[i]); swap(A, i, m); return m; } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 20

partition 1 r partition 1 must return the “middle”. int partition 1 (double[] A, int i, int j, double pivot) { // Shuffle elements of A[i. . j] so that elements // < pivot appear to the left of elements > pivot if (base case). . . if (A[i] <= pivot) // A[i] in correct half return partition 1(A, i+1, j, pivot); else if (A[j] > pivot) // A[j] in correct half return partition 1(A, i, j-1, pivot); else { // A[i] and A[j] in wrong half swap(A, i, j); return partition 1(A, i, j-1, pivot); } } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 21

partition 1 (cont. ) r Need to handle base cases. However, there is one key point to remember here: the index returned by partition 1 must contain a value less than the pivot, because it will be swapped back into A[i]. Base case needs to guarantee this: // Base case for partition 1: if (j == i) if (A[i] < pivot) return i; else return i-1; 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 22

Guessing the median r Making a good guess concerning the median is very important. r Here is a simple approach: int guess. Median. Location (double[] A, int i, int j) { return (i+j)/2; } 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 23

Final words on quicksort r Quicksort runs in time n log n, but only if the partitions are (roughly) in half. r Worst case performance for quicksort is quadratic, but it is difficult to find examples where it is inefficient. 21/3/00 SEM 107 - Kamin & Reddy Class 15 - Recursive Sorting - 24