Class 14 Intractable Problems CS 150 Computer Science

Class 14: Intractable Problems CS 150: Computer Science University of Virginia Computer Science David Evans http: //www. cs. virginia. edu/evans

Smileys Problem Input: n square tiles Output: Arrangement of the tiles in a square, where the colors and shapes match up, or “no, its impossible”. CS 150 Fall 2005: 2

Thanks to Peggy Reed for making the Smiley Puzzles!

Problems and Procedures • To know a O (f) bound for a problem, we need to find a (f) procedure that solves it – The sorting problem is O (n log n) since we know a procedure that solves it in (n log n) • To know a Ω(f ) bound for a problem, we need to prove that there is no procedure faster than (f) that solves it – We proved sorting is Ω(n log n) by reasoning about the number of decisions needed CS 150 Fall 2005: 4

How much work is the Smiley’s Problem? • Upper bound: (O) O (n!) Try all possible permutations • Lower bound: ( ) (n) Must at least look at every tile • Tight bound: ( ) No one knows! CS 150 Fall 2005: 5

Complexity Class P “Tractable” Class P: problems that can be solved in polynomial time O (nk) for some constant k. Easy problems like sorting, making a photomosaic using duplicate tiles, simulating the universe are all in P. CS 150 Fall 2005: 6

Complexity Class NP: problems that can be solved in nondeterministic polynomial time If we could try all possible solutions at once, we could identify the solution in polynomial time. Alternately: If we had a magic guess-correctly procedure that makes every decision correctly, we could devise a procedure that solves the problem in polynomial time. Note: this definition is not precise enough to be satisfying yet! We will need to understand better what a “step” means when we measure work to define this properly. CS 150 Fall 2005: 7

NP Problems • Can be solved by just trying all possible answers until we find one that is right • Easy to quickly check if an answer is right – Checking an answer is in P • The smileys problem is in NP We can easily try n! different answers We can quickly check if a guess is correct (check all n tiles) CS 150 Fall 2005: 8

Is the Smiley’s Problem in P? No one knows! We can’t find a O (nk) solution. We can’t prove one doesn’t exist. CS 150 Fall 2005: 9

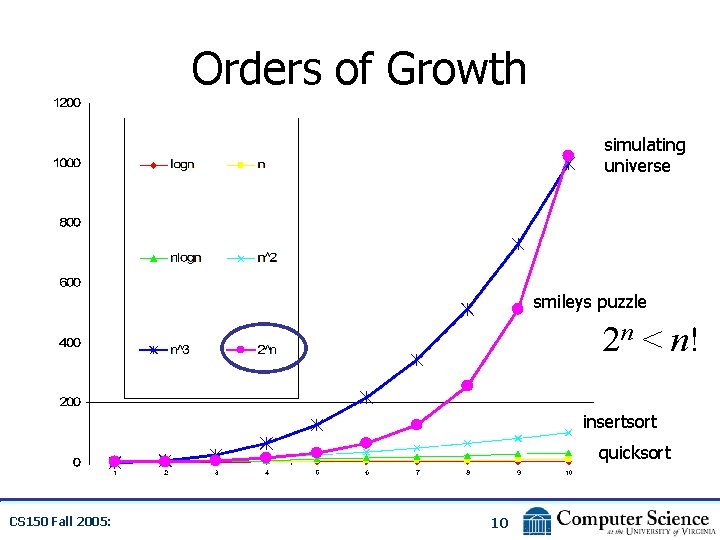
Orders of Growth simulating universe smileys puzzle 2 n < n! insertsort quicksort CS 150 Fall 2005: 10

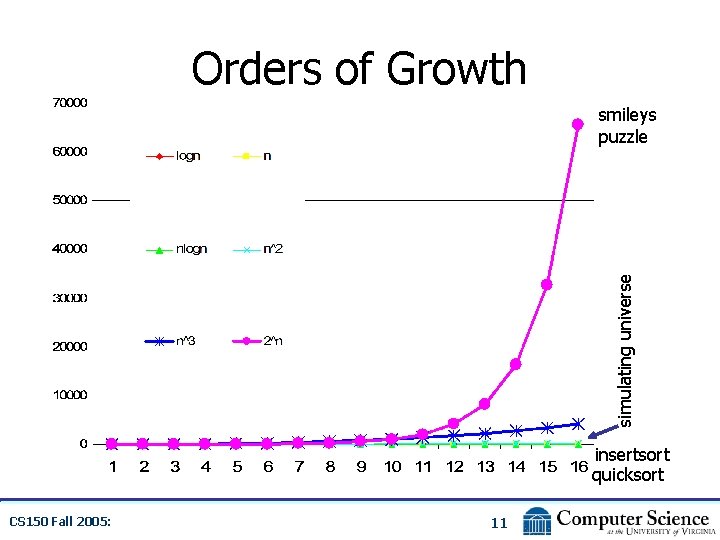
Orders of Growth simulating universe smileys puzzle insertsort quicksort CS 150 Fall 2005: 11

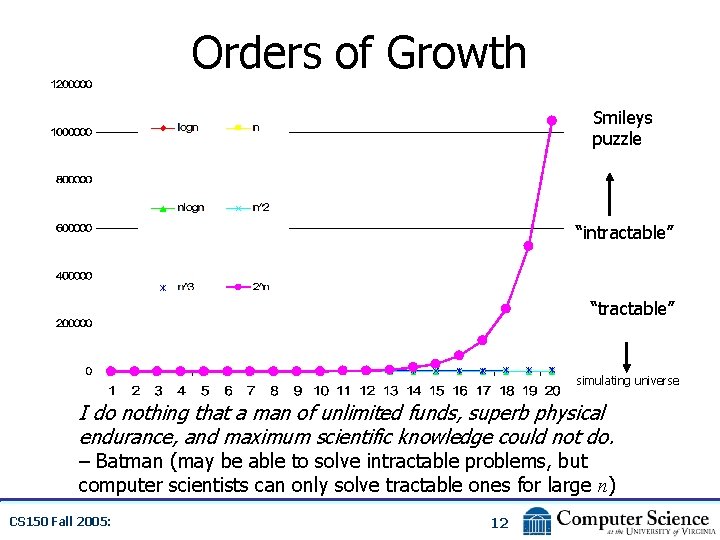
Orders of Growth Smileys puzzle “intractable” “tractable” simulating universe I do nothing that a man of unlimited funds, superb physical endurance, and maximum scientific knowledge could not do. – Batman (may be able to solve intractable problems, but computer scientists can only solve tractable ones for large n) CS 150 Fall 2005: 12

Quiz Break CS 150 Fall 2005: 13

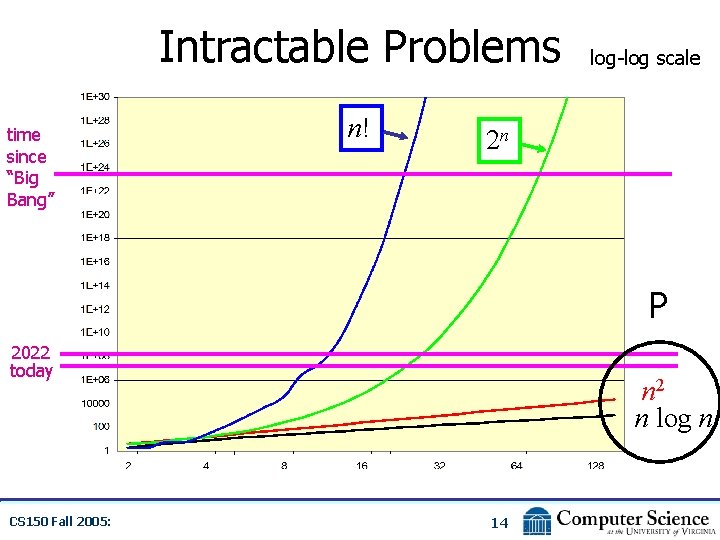
Intractable Problems time since “Big Bang” n! log-log scale 2 n P 2022 today CS 150 Fall 2005: n 2 n log n 14

Moore’s Law Doesn’t Help • If the fastest procedure to solve a problem is (2 n) or worse, Moore’s Law doesn’t help much. • Every doubling in computing power increases the problem size by 1. CS 150 Fall 2005: 15

P = NP? • Is there a polynomial-time solution to the “hardest” problems in NP? • No one knows the answer! • The most famous unsolved problem in computer science and math • Listed first on Millennium Prize Problems – win $1 M if you can solve it – (also an automatic A+ in this course) CS 150 Fall 2005: 16

This makes a huge difference! time since “Big Bang” 2032 today CS 150 Fall 2005: n! 2 n Solving a large smileys problem either takes a few seconds, or more time than the universe has been in existence. But, no one knows which for sure! log-log scale 17 n 2 n log n

Who cares about Smiley puzzles? If we had a fast (polynomial time) procedure to solve the smiley puzzle, we would also have a fast procedure to solve the 3/stone/apple/tower puzzle: 3 CS 150 Fall 2005: 18

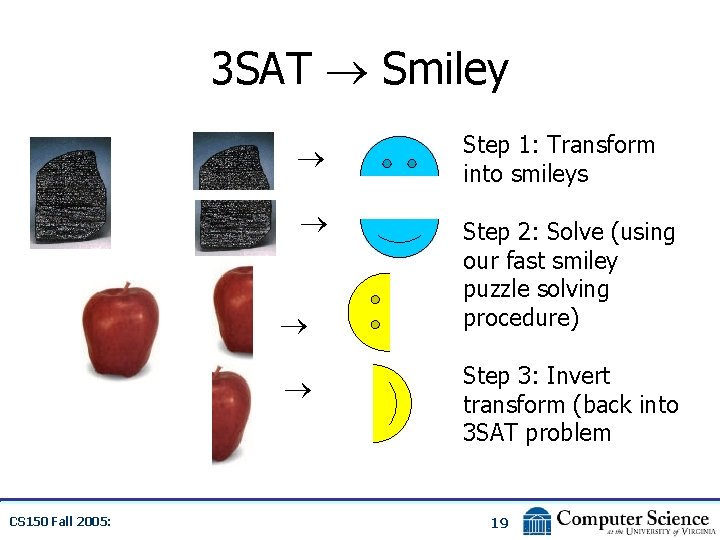
3 SAT Smiley CS 150 Fall 2005: Step 1: Transform into smileys Step 2: Solve (using our fast smiley puzzle solving procedure) Step 3: Invert transform (back into 3 SAT problem 19

The Real 3 SAT Problem (also can be quickly transformed into the Smileys Puzzle) CS 150 Fall 2005: 20

Propositional Grammar Sentence : : = Clause Sentence Rule: Evaluates to value of Clause : : = Clause 1 Clause 2 Or Rule: Evaluates to true if either clause is true Clause : : = Clause 1 Clause 2 And Rule: Evaluates to true iff both clauses are true CS 150 Fall 2005: 21

Propositional Grammar Clause : : = Clause Not Rule: Evaluates to the opposite value of clause ( true false) Clause : : = ( Clause ) Group Rule: Evaluates to value of clause. Clause : : = Name Rule: Evaluates to value associated with Name. CS 150 Fall 2005: 22

Proposition Example Sentence : : = Clause 1 Clause 2 Clause : : = ( Clause ) Clause : : = Name a (b c) b c CS 150 Fall 2005: 23 (or) (and) (not)

The Satisfiability Problem (SAT) • Input: a sentence in propositional grammar • Output: Either a mapping from names to values that satisfies the input sentence or no way (meaning there is no possible assignment that satisfies the input sentence) CS 150 Fall 2005: 24

SAT Example Sentence : : = Clause 1 Clause 2 Clause : : = ( Clause ) Clause : : = Name SAT (a (b c) { a: true, b: false, c: true } { a: true, b: true, c: false } SAT (a a) no way CS 150 Fall 2005: 25 (or) (and) (not)

The 3 SAT Problem • Input: a sentence in propositional grammar, where each clause is a disjunction of 3 names which may be negated. • Output: Either a mapping from names to values that satisfies the input sentence or no way (meaning there is no possible assignment that satisfies the input sentence) CS 150 Fall 2005: 26

3 SAT / SAT Is 3 SAT easier or harder than SAT? It is definitely not harder than SAT, since all 3 SAT problems are also SAT problems. Some SAT problems are not 3 SAT problems. CS 150 Fall 2005: 27

3 SAT Example Sentence : : = Clause 1 Clause 2 Clause : : = ( Clause ) Clause : : = Name 3 SAT ( (a b c) ( a b d) ( a b d) (b c d ) ) { a: true, b: false, c: false, d: false} CS 150 Fall 2005: 28 (or) (and) (not)

3 SAT Smiley • Like 3/stone/apple/tower puzzle, we can convert every 3 SAT problem into a Smiley Puzzle problem! • Transformation is more complicated, but still polynomial time. • So, if we have a fast (P) solution to Smiley Puzzle, we have a fast solution to 3 SAT also! CS 150 Fall 2005: 29

NP Complete • Cook and Levin proved that 3 SAT was NPComplete (1971) • A problem is NP-complete if it is as hard as the hardest problem in NP • If 3 SAT can be transformed into a different problem in polynomial time, than that problem must also be NP-complete. • Either all NP-complete problems are tractable (in P) or none of them are! CS 150 Fall 2005: 30

Charge • PS 4 is due Monday • More on P vs. NP next class CS 150 Fall 2005: 31