CLASE 8 PARTE 1 CONTINUIDAD DE FUNCIONES DE



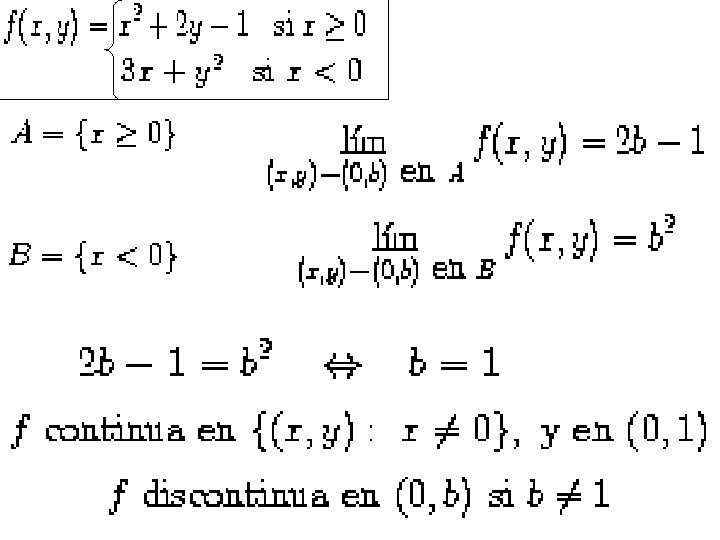







- Slides: 13

CLASE 8 PARTE 1: CONTINUIDAD DE FUNCIONES DE VARIAS VARIABLES. Bibliografía de la Clase 8: • Juan de Burgos: Cálculo Infinitesimal en Varias Variables. Capítulo 1, sección 1. 3, parágrafos 15, 16 y 17. Ejercicios para las clase 8 • Práctico 3 del año 2006. Cálculo Diferencial e Integral II. Eleonora Catsigeras. IMERL. Fac. de Ingeniería. Udela. R. J. Herrera y Reissig 565. Montevideo. Uruguay. Agosto 2006. Derechos reservados.

Sea dada (no se define continuidad en puntos a que no pertenecen al dominio de D) DEFINICIÓN. Continuidad de f en el punto a: si DEFINICIÓN. Continuidad de f en el conjunto D si

TEOREMA OBSERVACIÓN: puede o no existir, pero si existe, es diferente de f(a) EJEMPLO: Encontrar los puntos de continuidad y discontinuidad de la siguiente función:
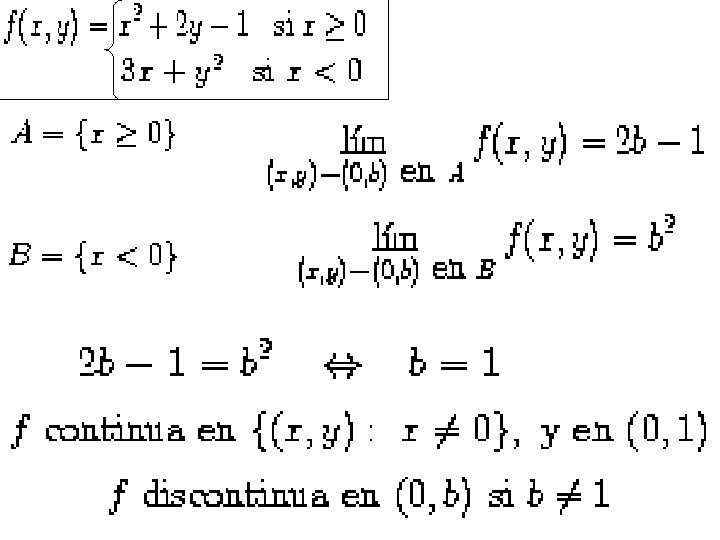

CLASE 8 PARTE 2: PROPIEDADES DE LA CONTINUIDAD Bibliografía de la Clase 8: • Juan de Burgos: Cálculo Infinitesimal en Varias Variables. Capítulo 1, sección 1. 3, parágrafos 15, 16 y 17. Ejercicios para las clase 8 • Práctico 3 del año 2006. Cálculo Diferencial e Integral II. Eleonora Catsigeras. IMERL. Fac. de Ingeniería. Udela. R. J. Herrera y Reissig 565. Montevideo. Uruguay. Agosto 2006. Derechos reservados.

1. FUNCIONES VECTORIALES CONTINUAS 2. FUNCIÓN REAL CONTINUA CONSERVA EL SIGNO EN UN ENTORNO DEL PUNTO DONDE ES NO NULA

3. La suma de funciones continuas es continua. 4. El producto de una función continua por el escalar continuo, es continuo. 5. La composición de funciones continuas es continua.

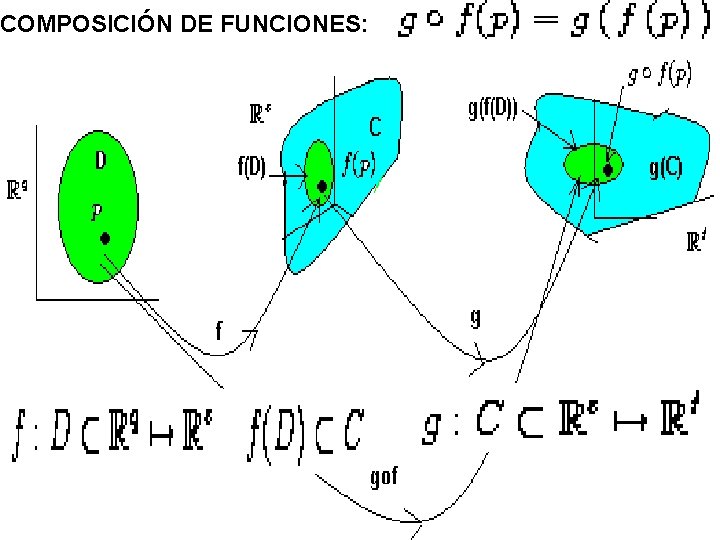
COMPOSICIÓN DE FUNCIONES:

Dem. que la composición de funciones continuas es continua.

CLASE 8 PARTE 3: CARACTERIZACIÓN DE LA CONTINUIDAD Bibliografía de la Clase 8: • Juan de Burgos: Cálculo Infinitesimal en Varias Variables. Capítulo 1, sección 1. 3, parágrafos 15, 16 y 17. Ejercicios para las clase 8 • Práctico 3 del año 2006. Cálculo Diferencial e Integral II. Eleonora Catsigeras. IMERL. Fac. de Ingeniería. Udela. R. J. Herrera y Reissig 565. Montevideo. Uruguay. Agosto 2006. Derechos reservados.

TEOREMA (Caracterización de la continuidad por abiertos. ) Una función es continua si y solo si la preimagen de cualquier abierto es un conjunto abierto.

Dem. Directo:

Dem. Recíproco: