Clase 3 Ciencia de los materiales Facultad de

Clase 3: Ciencia de los materiales Facultad de ciencias económicas y administrativas Departamento de calidad y producción

La estructura cristalina de los sólidos Temas a tratar ¿Como se ensamblan los átomos dentro de las estructuras sólidas (nos enfocaremos en los metales) ¿ cómo la densidad de un material depende de su estructura? ¿ Cuándo las propiedades del material varian con la orientación de la muestra? 2

CONTENIDO 1. Introducción 2. Estructuras cristalinas Sistemas cristalinos Factores de empaquetamiento Densidad teórica Direcciones y planos cristalográficos Estudios de rayos X Estructuras importantes 3. Estructuras no cristalinas Estruturas amorfas Cristal de monogranate 3

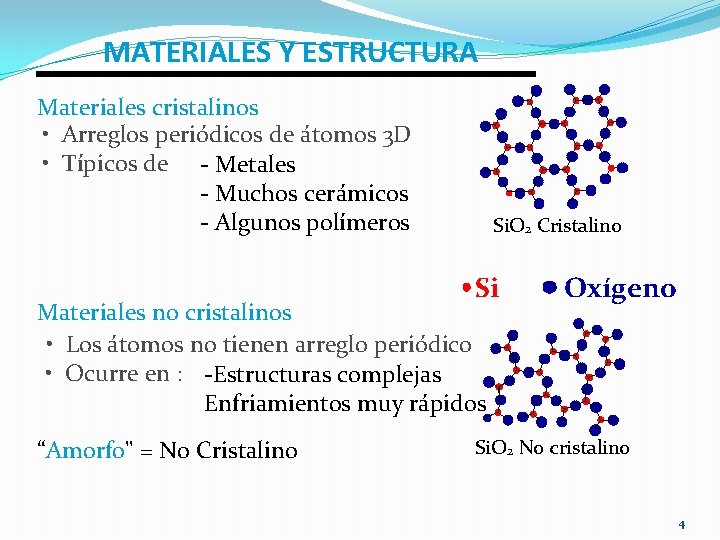
MATERIALES Y ESTRUCTURA Materiales cristalinos • Arreglos periódicos de átomos 3 D • Típicos de - Metales - Muchos cerámicos - Algunos polímeros Si. O 2 Cristalino Si Materiales no cristalinos • Los átomos no tienen arreglo periódico • Ocurre en : -Estructuras complejas Enfriamientos muy rápidos “Amorfo" = No Cristalino Oxígeno Si. O 2 No cristalino 4

Redes, Celdas Unitarias, Bases y Estructuras Cristalinas o Red – Es una colección de puntos (puntos de red) ordenados en un patrón periódico. o Celda unitaria – Una subdivisión de una red que sigue conservando las características generales de la red. o Parámetro de red – describen el tamaño y la forma de la celda unitaria (aristas y ángulos).

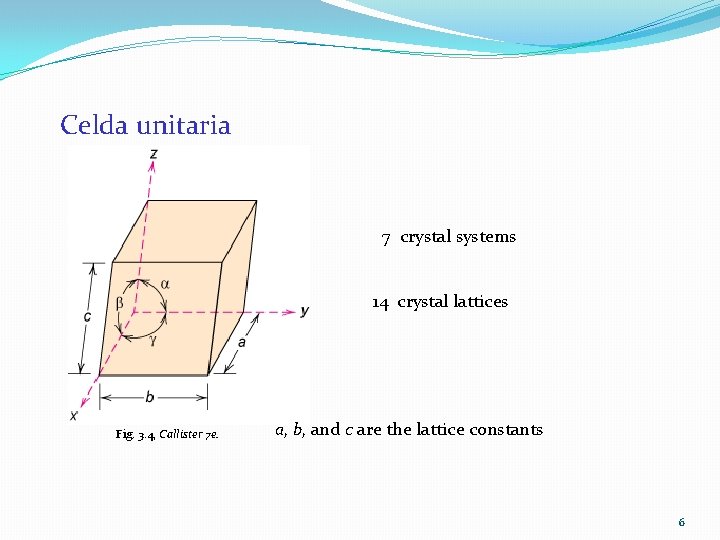
Celda unitaria 7 crystal systems 14 crystal lattices Fig. 3. 4, Callister 7 e. a, b, and c are the lattice constants 6

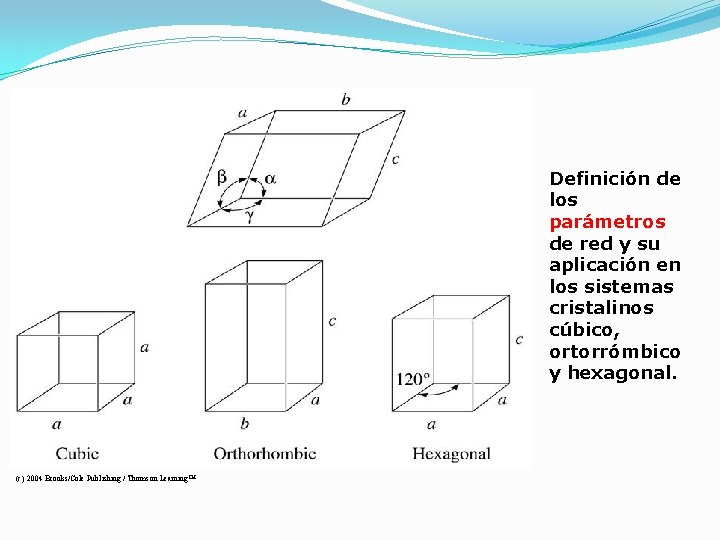
Definición de los parámetros de red y su aplicación en los sistemas cristalinos cúbico, ortorrómbico y hexagonal. (c) 2004 Brooks/Cole Publishing / Thomson Learning™

Parámetro de red Características de los siete sistemas cristalinos

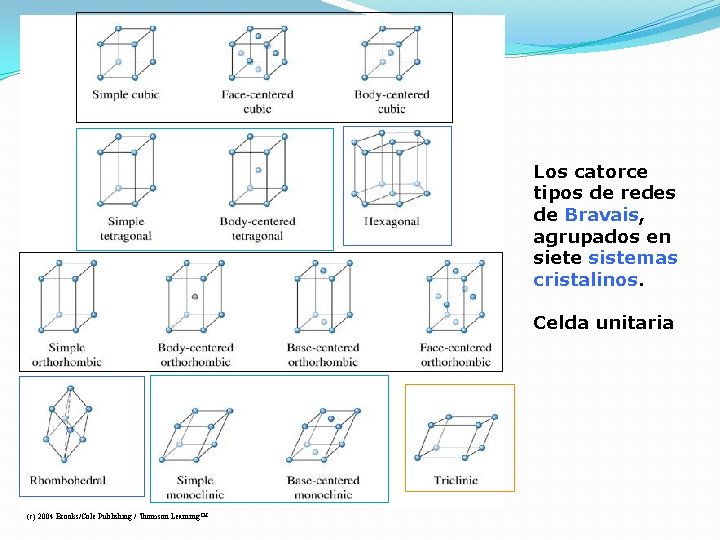
Los catorce tipos de redes de Bravais, agrupados en siete sistemas cristalinos. Celda unitaria (c) 2004 Brooks/Cole Publishing / Thomson Learning™

Muestras de Cristales cúbico tetragonal ortorrómbico monoclínico triclínico hexagonal

o Cantidad de átomos por celda – cantidad especifica de puntos de red. o Radio atómico Vs. Parámetro de red – las direcciones compactas son las direcciones a lo largo de las cuales los átomos están en contacto continuo.

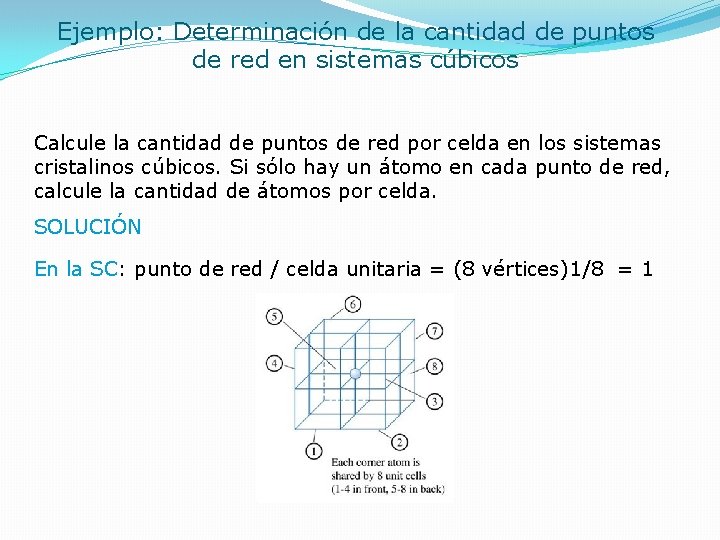
Ejemplo: Determinación de la cantidad de puntos de red en sistemas cúbicos Calcule la cantidad de puntos de red por celda en los sistemas cristalinos cúbicos. Si sólo hay un átomo en cada punto de red, calcule la cantidad de átomos por celda. SOLUCIÓN En la SC: punto de red / celda unitaria = (8 vértices)1/8 = 1

Estructura cristalina metálica �Tiende a ser densamente empaquetada. Razones para el empaquetamiento denso: �únicamente un elemento esta presente, por lo tanto todos los radios atómicos son los mismos. �Tienen estructuras cristalinas simples

• Factor de empaquetamiento – fracción del espacio ocupada por átomos, suponiendo que son esferas duras. • Radio atómico – Radio aparente de un átomo, comúnmente calculado a partir de las dimensiones de la celda unitaria, usando direcciones compactas (depende del número de coordinación). • Numero de coordinación – cantidad de átomos vecinos más cercanos a determinado átomo.

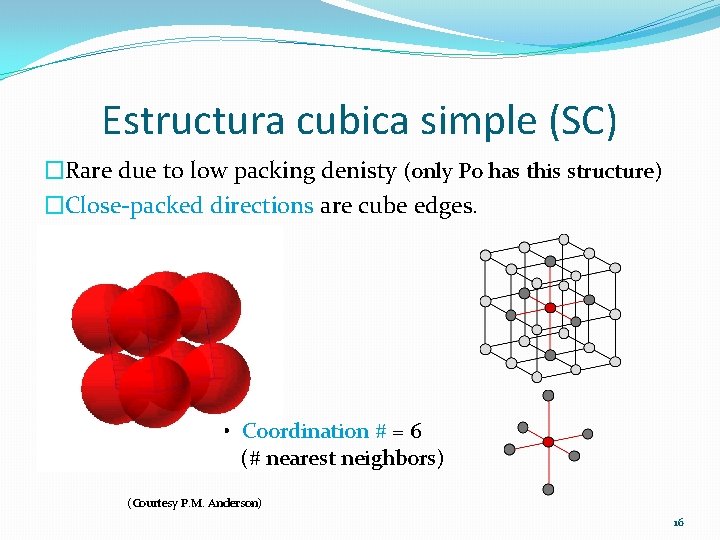
Estructura cubica simple (SC) �Rare due to low packing denisty (only Po has this structure) �Close-packed directions are cube edges. • Coordination # = 6 (# nearest neighbors) (Courtesy P. M. Anderson) 16

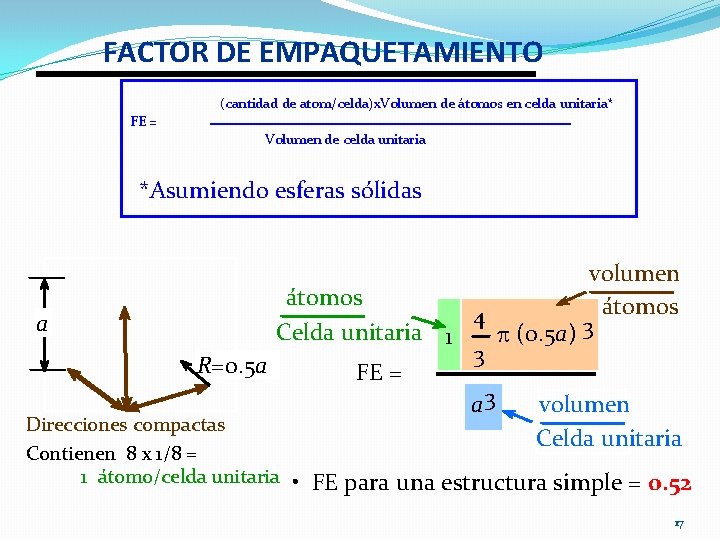
FACTOR DE EMPAQUETAMIENTO (cantidad de atom/celda)x. Volumen de átomos en celda unitaria* FE = Volumen de celda unitaria *Asumiendo esferas sólidas a volumen átomos 4 Celda unitaria 1 p (0. 5 a) 3 3 R=0. 5 a FE = a 3 volumen Direcciones compactas Contienen 8 x 1/8 = 1 átomo/celda unitaria Celda unitaria • FE para una estructura simple = 0. 52 17

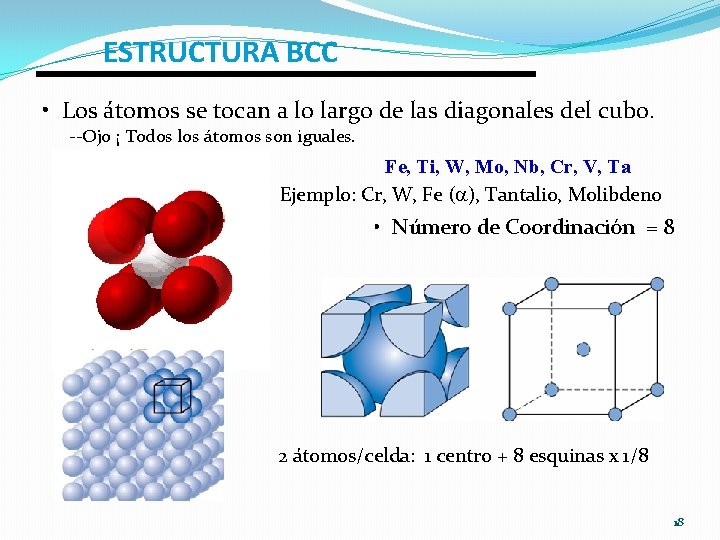
ESTRUCTURA BCC • Los átomos se tocan a lo largo de las diagonales del cubo. --Ojo ¡ Todos los átomos son iguales. Fe, Ti, W, Mo, Nb, Cr, V, Ta Ejemplo: Cr, W, Fe ( ), Tantalio, Molibdeno • Número de Coordinación = 8 2 átomos/celda: 1 centro + 8 esquinas x 1/8 18

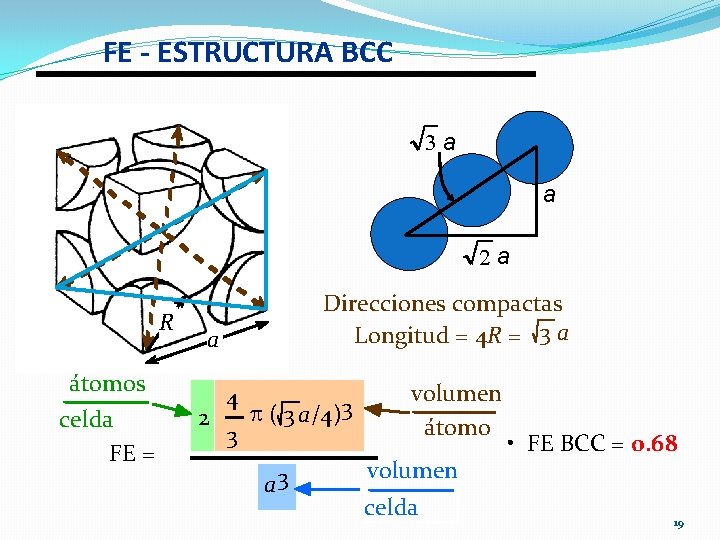
FE - ESTRUCTURA BCC 3 a a 2 a R átomos celda FE = Direcciones compactas Longitud = 4 R = 3 a a 2 4 3 p ( 3 a/4)3 a 3 volumen átomo volumen celda • FE BCC = 0. 68 19

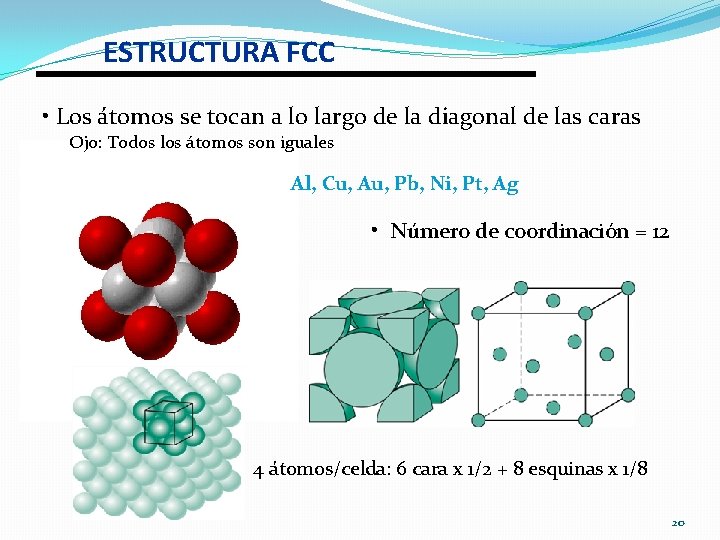
ESTRUCTURA FCC • Los átomos se tocan a lo largo de la diagonal de las caras Ojo: Todos los átomos son iguales Al, Cu, Au, Pb, Ni, Pt, Ag • Número de coordinación = 12 4 átomos/celda: 6 cara x 1/2 + 8 esquinas x 1/8 20

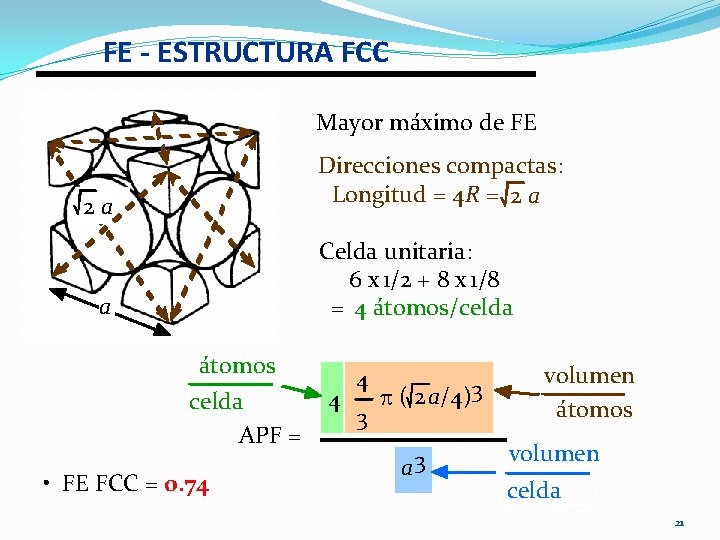
FE - ESTRUCTURA FCC Mayor máximo de FE 2 a a Direcciones compactas: Longitud = 4 R = 2 a Celda unitaria: 6 x 1/2 + 8 x 1/8 = 4 átomos/celda átomos volumen 4 p ( 2 a/4)3 4 celda átomos 3 APF = volumen a 3 • FE FCC = 0. 74 celda 21

Determine el factor de empaquetamiento (FE), para la estructura hexagonal compacta. • ABAB. . . Secuencia de apilamiento • Proyección 3 D c • Proyección 2 D A Plano superior B Plano intermedio A Plano inferior a • FE = ? 6 átomos/Celda ej: Cd, Mg, Ti, Zn 22

Estructura hexagonal compacta

DENSIDAD TEÓRICA Densidad = = = Masa de átomos en celda unitaria Volumen de celda unitaria n A V C NA Donde n = número of átomos/celda A = Peso atómico VC = Volumen de celda unitaria NA = Número de Avogadro = 6. 023 x 1023 átomos/mol 25

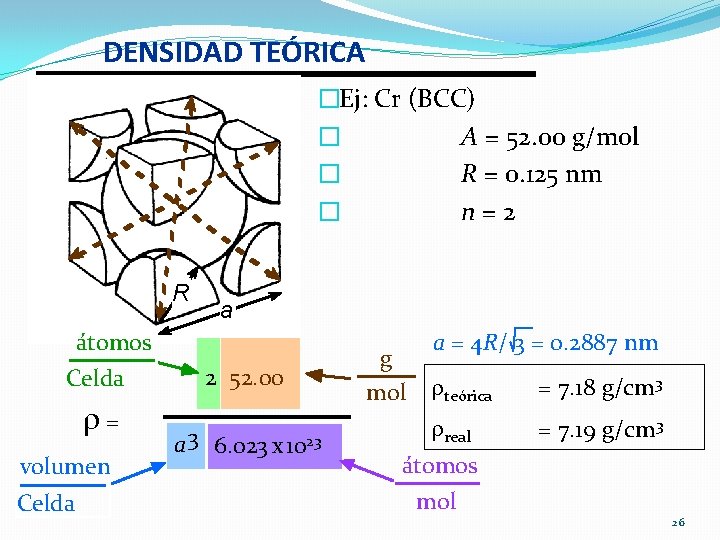
DENSIDAD TEÓRICA �Ej: Cr (BCC) � A = 52. 00 g/mol � R = 0. 125 nm � n = 2 R átomos Celda = volumen Celda a 2 52. 00 a 3 6. 023 x 1023 g mol a = 4 R/ 3 = 0. 2887 nm teórica = 7. 18 g/cm 3 real = 7. 19 g/cm 3 átomos mol 26

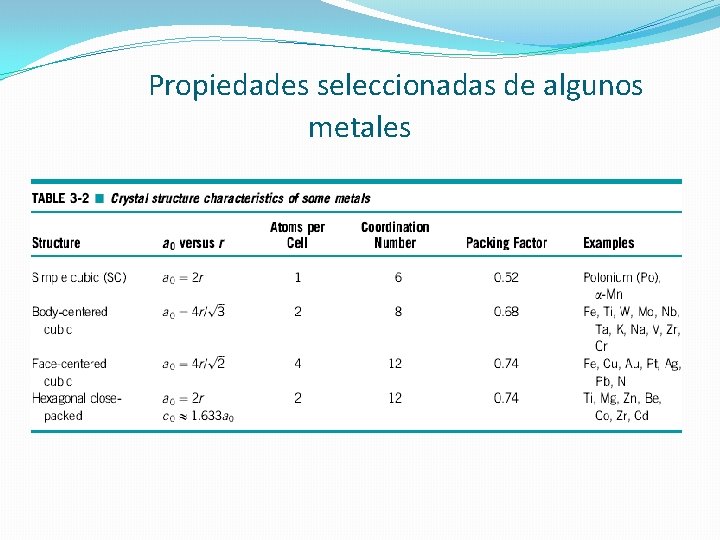
Propiedades seleccionadas de algunos metales

DENSIDAD TEÓRICA Metales presentan. . . • Ordenamientos compacto (Enlaces metálicos) • Grandes masas atómicas Cerámicos presentan. . . • Ordenamiento menos compactos • Elemento ligeros 3 (g/cm ) En general metales > cerámicos > polímeros 30 Por qué? Polimeros presentan • Ordenamientos no compactos (o amorfos) • Elementos muy livianos (C, H, O) Metals/ Alloys 20 Platinum Gold, W Tantalum 10 Silver, Mo Cu, Ni Steels Tin, Zinc 5 4 3 2 1 0. 5 0. 4 0. 3 Graphite/ Ceramics/ Semicond Polymers Composites/ fibers B *GFRE, CFRE, & AFRE are Glass, Carbon, & Aramid Fiber-Reinforced Epoxy composites (values based on 60% volume fraction of aligned fibers in an epoxy matrix). Zirconia Titanium Al oxide Diamond Si nitride Aluminum Glass -soda Concrete PTFE Silicon Magnesium G raphite Silicone PVC PET PC HDPE, PS PP, LDPE Glass fibers GFRE* Carbon fibers CFRE * Aramid fibers AFRE * Wood 28

Ejemplo 2 Determinación de la densidad del hierro BCC Determine la densidad del hierro BCC, cuyo parámetro de red es 0, 2866 nm. SOLUCIÓN Átomos/celda = 2; a 0 = 0, 2866 nm = 2, 866 10 -8 cm Masa atómica = 55, 847 g/mol Volumen de cm 3/celda = = (2. 866 10 -8 cm)3 = 23. 54 10 -24 Número de Avogadro NA = 6. 02 1023 átomos/mol

Ejemplo 2 Tarea �Determine la densidad del cobre FCC, cuyo parámetro de red es 0, 3615 nm. �Determine la densidad del vanadio BCC, cuyo parámetro de red es 0, 3027 nm.

Crystals as Building Blocks • Some engineering applications require single crystals: --diamond single crystals for abrasives (Courtesy Martin Deakins, GE Superabrasives, Worthington, OH. Used with permission. ) --turbine blades Fig. 8. 33(c), Callister 7 e. (Fig. 8. 33(c) courtesy of Pratt and Whitney). • Properties of crystalline materials often related to crystal structure. --Ex: Quartz fractures more easily along some crystal planes than others. (Courtesy P. M. Anderson) 31

Comportamiento isotrópico y anisotrópico �Un material es cristalográficamente anisotrópico si sus propiedades dependen de la dirección cristalográfica en la cual se mide la propiedad. �Si las propiedades son idénticas en todas las direcciones, el material, es cristalográficamente isotrópico, (materiales policristalinos). �Grano: cristal pequeño en un material policristalino.

Anisotropic • Most engineering materials are polycrystals. 1 mm • Nb-Hf-W plate with an electron beam weld. • Each "grain" is a single crystal. • If grains are randomly oriented, Adapted from Fig. K, color inset pages of Callister 5 e. (Fig. K is courtesy of Paul E. Danielson, Teledyne Wah Chang Albany) Isotropic overall component properties are not directional. • Grain sizes typ. range from 1 nm to 2 cm (i. e. , from a few to millions of atomic layers). 33

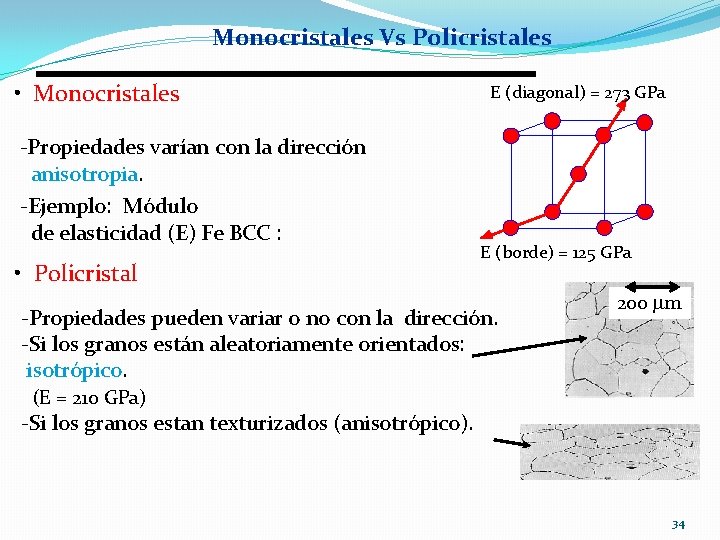
Monocristales Vs Policristales • Monocristales -Propiedades varían con la dirección anisotropia. -Ejemplo: Módulo de elasticidad (E) Fe BCC : • Policristal E (diagonal) = 273 GPa E (borde) = 125 GPa -Propiedades pueden variar o no con la dirección. -Si los granos están aleatoriamente orientados: isotrópico. (E = 210 GPa) -Si los granos estan texturizados (anisotrópico). 200 mm 34

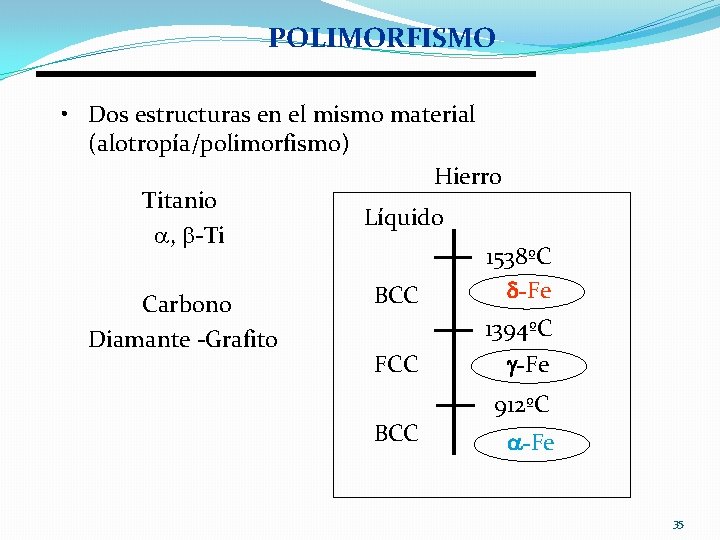
POLIMORFISMO • Dos estructuras en el mismo material (alotropía/polimorfismo) Hierro Titanio Líquido , -Ti 1538ºC -Fe BCC Carbono 1394ºC Diamante -Grafito -Fe FCC BCC 912ºC -Fe 35

CAMBIOS DE VOLUMEN: TRANSFORMACIONES • Calcule el cambio volumétrico porcentual cuando la zirconia pasa de una estructura tetragonal a una monoclínica. • a= 5. 156Å; b= 5. 191Å ; c= 5. 304Å; β=98. 9° • A= 5. 094Å y c= 5. 304Å • Durante la transformación ¿ se expande o se contrae la zirconia? ¿ cuales son los efectos de esta transformación sobre las propiedades mecánicas de la cerámica de zirconia? 36

Example 3. 5 SOLUTION The volume of a tetragonal unit cell is given by (5. 094)2 (5. 304) = 134. 33 Å3. V = a 2 c = The volume of a monoclinic unit cell is given by β = (5. 156) (5. 191) (5. 304) sin(98. 9) = 140. 25 Å3. V = abc sin Thus, there is an expansion of the unit cell as Zr. O 2 transforms from a tetragonal to monoclinic form. The percent change in volume = (final volume initial volume)/(initial volume) 100 = (140. 25 - 134. 33 Å3)/140. 25 Å3 * 100 = 4. 21%. Most ceramics are very brittle and cannot withstand more than a 0. 1% change in volume. The conclusion here is that Zr. O 2 ceramics cannot be used in their monoclinic form since, when zirconia does transform to the tetragonal form, it will most likely fracture. Therefore, Zr. O 2 is often stabilized in a cubic form using different additives such as Ca. O, Mg. O, and Y 2 O 3.

Puntos, Direcciones y Planos en la Celda Unitaria o Coordenadas de puntos – se escriben con base en las tres dimensiones y los números se separan comas. o Índices de Miller - notación abreviada para describir ciertas direcciones cristalográficas y planos en un material. o Importancia de las direcciones – se usan para indicar determinada orientación de un solo cristal o material policristalino. o Importancia de los planos – Los metales se deforman a lo largo de ciertos planos de átomos.

Coordenadas de puntos seleccionados en la celda unitaria. El número indica la distancia al origen, en términos de parámetros de red.

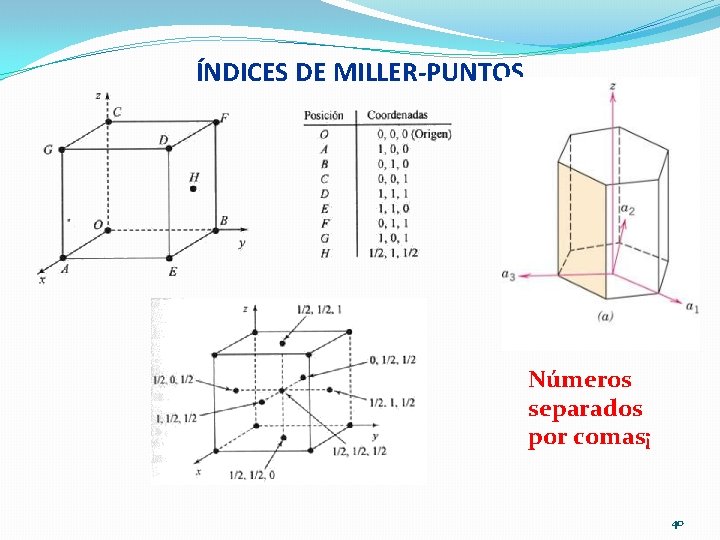
ÍNDICES DE MILLER-PUNTOS Números separados por comas¡ 40

Determinación de los Índices de Miller de Direcciones Determine los índices de Miller de las direcciones A, B y C de la Figura. Direcciones cristalográficas y coordenadas (c) 2004 Brooks/Cole Publishing / Thomson Learning™

Pasos para la solución: 1. 2. 3. 4. Determine las coordenadas de dos puntos que estén en esa dirección. Reste las coordenadas del punto "cabeza" de las coordenadas del punto "cola". Reduzca las fracciones y/o los resultados obtenidos de la resta en mínimos enteros. Encierre los números en corchetes [ ]. El signo negativo se representa con una barra sobre el número.

SOLUCIÓN Dirección A 1. Los dos puntos son 1, 0, 0, y 0, 0, 0 2. 1, 0, 0, – 0, 0, 0 = 1, 0, 0 3. No hay fracciones que eliminar o enteros a reducir 4. [100] Dirección B 1. Los dos puntos son 1, 1, 1 y 0, 0, 0 2. 1, 1, 1, – 0, 0, 0 = 1, 1, 1 3. No hay fracciones que eliminar o enteros a reducir 4. [111] Dirección C 1. Los dos puntos son 0, 0, 1 y 1/2, 1, 0 2. 0, 0, 1 – 1/2, 1, 0 = – 1/2, – 1, 1 3. 2(-1/2, -1, 1) = -1, -2, 2

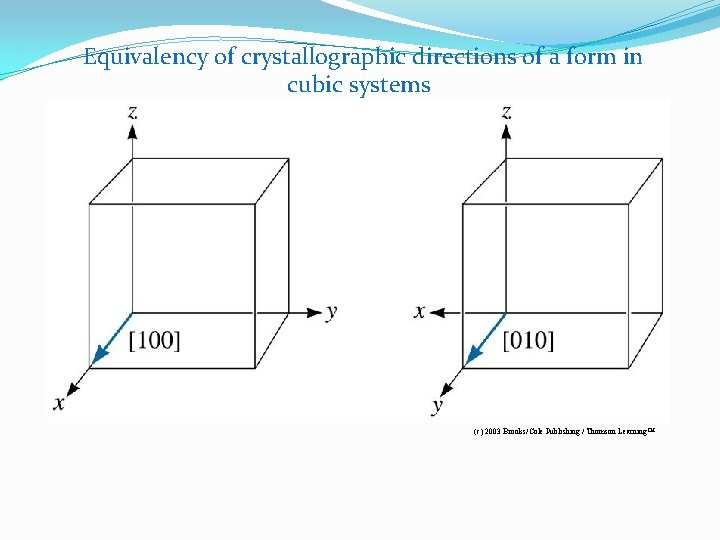
Equivalency of crystallographic directions of a form in cubic systems (c) 2003 Brooks/Cole Publishing / Thomson Learning™

Direcciones de la familia <110> en sistemas cúbicos

Importancia de las direcciones cristalográficas � Indican determinada orientación de un solo cristal o de un material policristalino. Ejemplos: � Los metales se deforman con más facilidad en direcciones a lo largo de las cuales los átomos están en contacto más estrecho (direcciones compactas). � Aplicaciones magnéticas: - núcleos de transformadores. - materiales magnéticos para medios de grabación. • Propiedades de resistencia: - cristales con los que se fabrican los álabes de las turbinas.

Planos en la celda unitaria � Los metales se deforman a lo largo de planos de átomos que estén empacados de la manera más compacta ( planos compactos). Ejemplos: � Crecimiento de cristales [ materiales electrónicos en forma de películas delgadas ( Si ó Ga. As)]

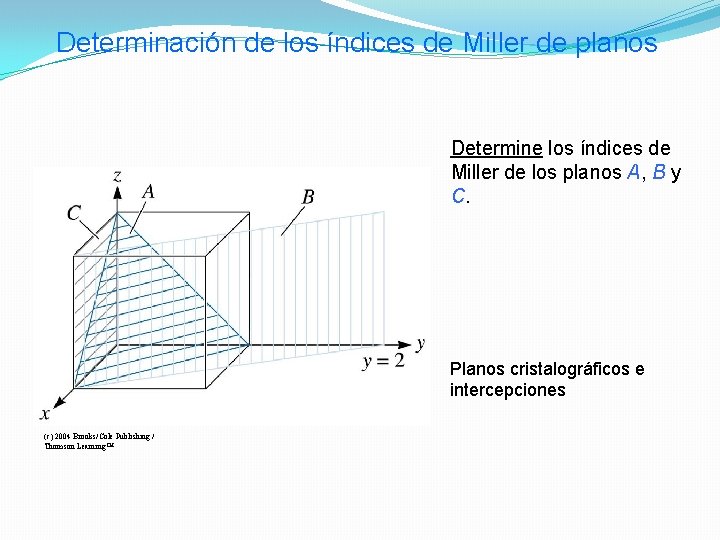
Determinación de los índices de Miller de planos Determine los índices de Miller de los planos A, B y C. Planos cristalográficos e intercepciones (c) 2004 Brooks/Cole Publishing / Thomson Learning™

Pasos para la solución: 1. 2. 3. 4. Identifique los puntos en donde el plano cruza los ejes x, y y z. Si el sistema cruza por el origen, mover el origen del sistema de coordenadas. Obtenga los recíprocos de esas intersecciones. Simplifique fracciones, pero no a mínimos enteros. Encierre los números en corchetes ( ). El signo negativo se representa con una barra sobre el número.

SOLUCIÓN Plano A 1. x = 1, y = 1, z = 1 2. 1/x = 1, 1/y = 1, 1 /z = 1 3. No hay fracciones que eliminar 4. (111) Plano B 1. El plano nunca intercepta el eje Z, por lo que x = 1, y = 2 y z = ∞ 2. 1/x = 1, 1/y =1/2, 1/z = 0 3. Eliminar fracciones: 1/x = 2, 1/y = 1, 1/z = 0 4. (210) Plano C 1. Se debe cambiar el origen, porque el plano pasa por 0, 0, 0. Nos movemos un parámetro de red en dirección y. Entonces, x = ∞, y = -1, y z = ∞ 2. 1/x = 0, 1/y = 1, 1/z = 0 3. No hay fracciones que eliminar

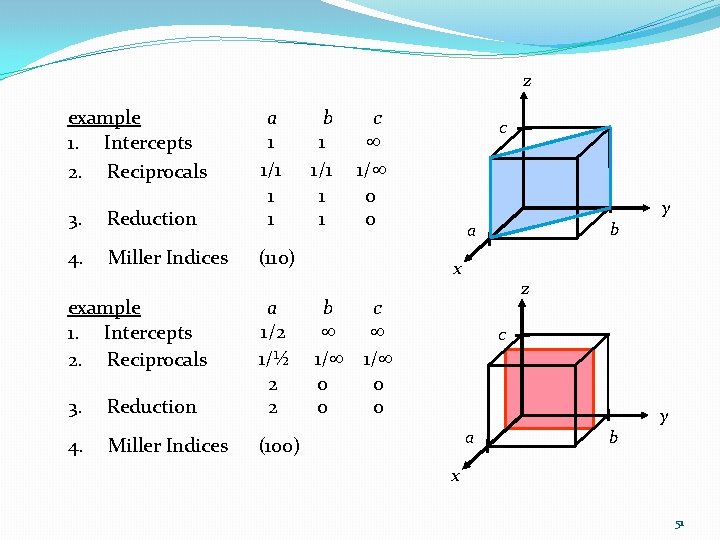
z example 1. Intercepts 2. Reciprocals 3. Reduction a b c 1 1/1 1/ 1 1 0 4. Miller Indices (110) example 1. Intercepts 2. Reciprocals 3. Reduction c y b a x z a b c 1/2 1/½ 1/ 1/ 2 0 0 c y a 4. Miller Indices (100) b x 51

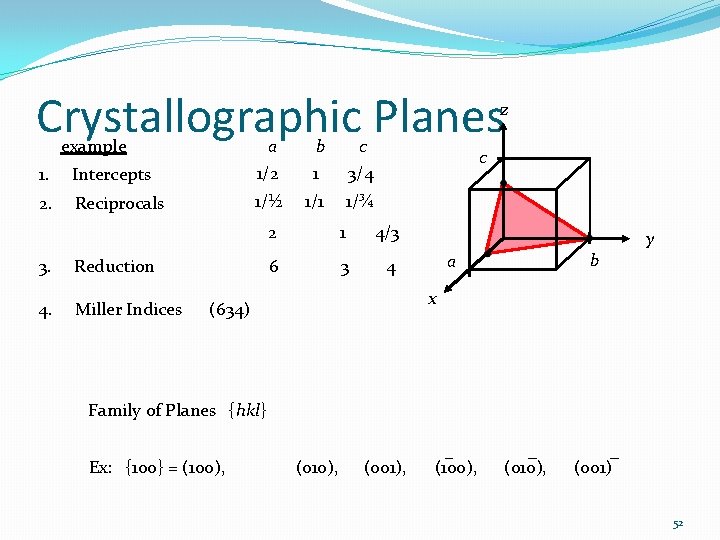
Crystallographic Planes z example 1. Intercepts a b c 1/2 1 3/4 2. Reciprocals 1/½ 1/1 1/¾ 3. Reduction 2 1 4/3 6 3 4 c y b a x 4. Miller Indices (634) Family of Planes {hkl} Ex: {100} = (100), (010), (001), (100), (010), (001) 52

Índices de Miller-Bravais para celdas unitarias hexagonales � Simetría exclusiva del sistema. � El procedimiento para determinar los índices de planos es exactamente igual a los anteriores, pero con cuatro intersecciones (hkil).

En las celdas unitarias HCP se obtienen los índices de Miller-Bravais usando un sistema coordenado de cuatro ejes. (c) 2004 Brooks/Cole Publishing / Thomson Learning™

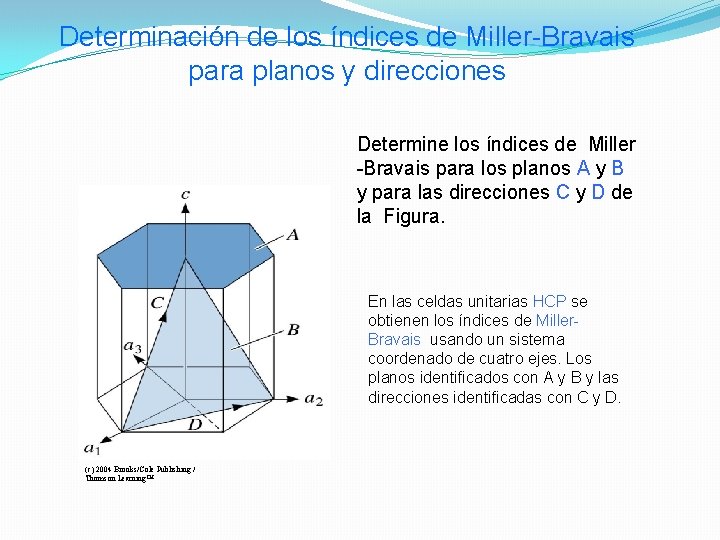
Determinación de los índices de Miller-Bravais para planos y direcciones Determine los índices de Miller -Bravais para los planos A y B y para las direcciones C y D de la Figura. En las celdas unitarias HCP se obtienen los índices de Miller. Bravais usando un sistema coordenado de cuatro ejes. Los planos identificados con A y B y las direcciones identificadas con C y D. (c) 2004 Brooks/Cole Publishing / Thomson Learning™

SOLUCION Plano A 1. a 1 = a 2 = a 3 = , c = 1 2. 1/a 1 = 1/a 2 = 1/a 3 = 0, 1/c = 1 3. No hay fracciones para simplificar 4. (0001) Plano B 1. a 1 = 1, a 2 = 1, a 3 = -1/2, c = 1 2. 1/a 1 = 1, 1/a 2 = 1, 1/a 3 = -2, 1/c = 1 3. No hay fracciones para simplificar 4. Dirección C 1. Los dos puntos son 0, 0, 1 y 1, 0, 0. 2. 0, 0, 1, -1, 0, 0 = 1, 0, 1 3. No hay fracciones para simplificar. 4.

SOLUCION (Continuación) Direction D 1. Los dos puntos son 0, 1, 0 and 1, 0, 0. 2. 0, 1, 0, -1, 0, 0 = -1, 1, 0 3. No hay fracciones para simplificar. 4.

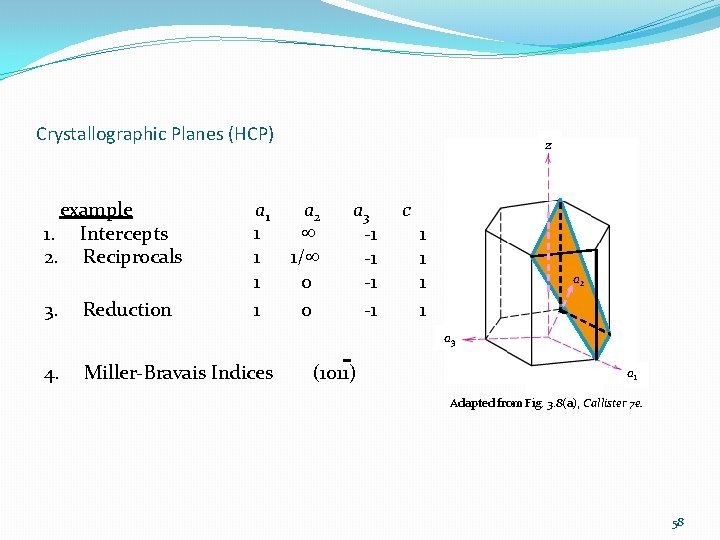
Crystallographic Planes (HCP) example 1. Intercepts 2. Reciprocals 3. Reduction z a 1 a 2 a 3 c 1 -1 1 1/ -1 1 0 -1 1 1 a 2 a 3 4. Miller-Bravais Indices (1011) a 1 Adapted from Fig. 3. 8(a), Callister 7 e. 58

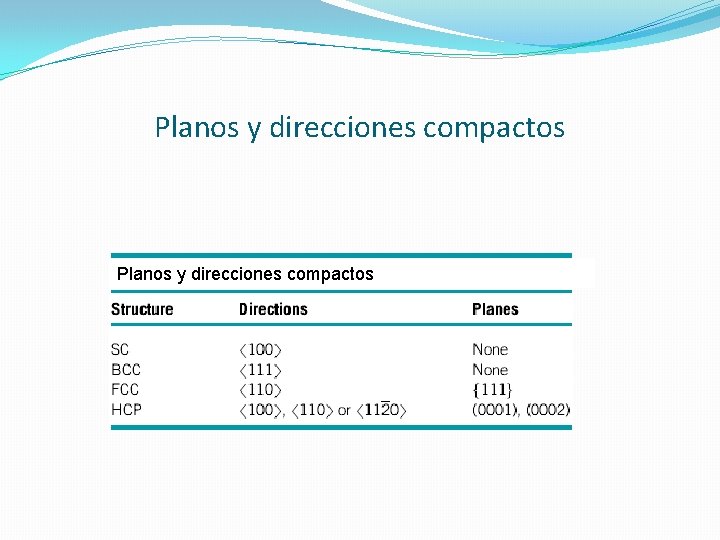
Planos y direcciones compactos

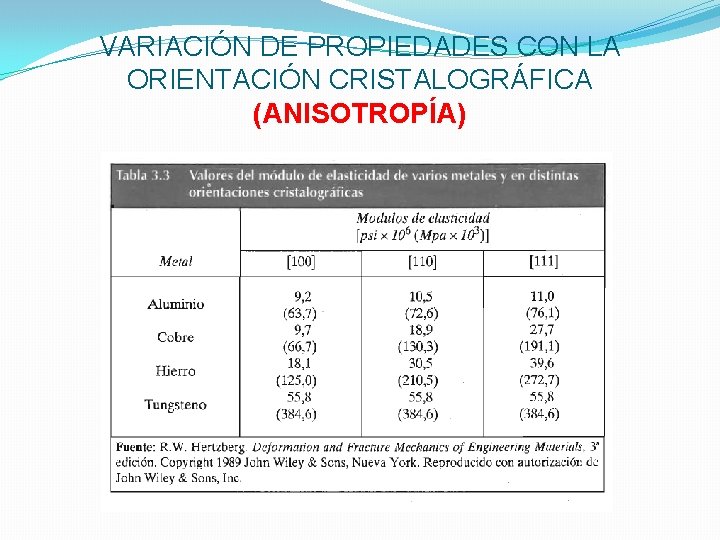
VARIACIÓN DE PROPIEDADES CON LA ORIENTACIÓN CRISTALOGRÁFICA (ANISOTROPÍA)

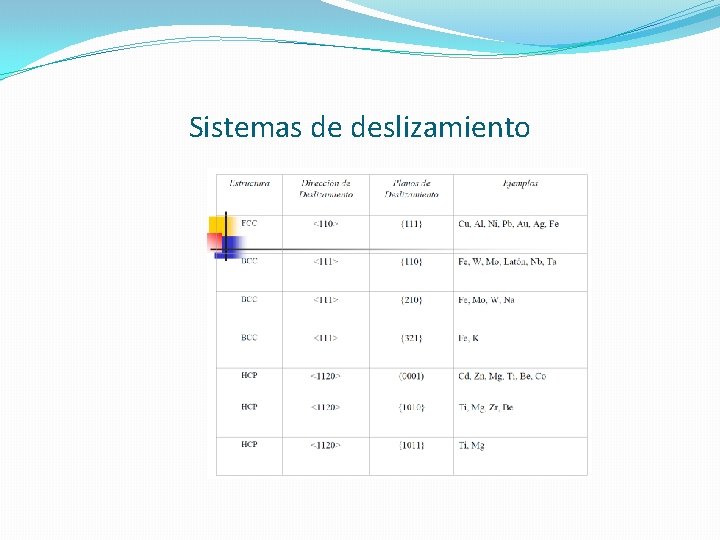
SISTEMAS DE DESLIZAMIENTO �Un sistema de deslizamiento es la combinación de un plano y una dirección que se halla sobre el plano a lo largo del cual se produce el deslizamiento. �El Mecanismo de deslizamiento puede definirse como el movimiento paralelo de dos regiones cristalinas adyacentes, una respecto a la otra, a través de algún plano (o planos).

Sistemas de deslizamiento

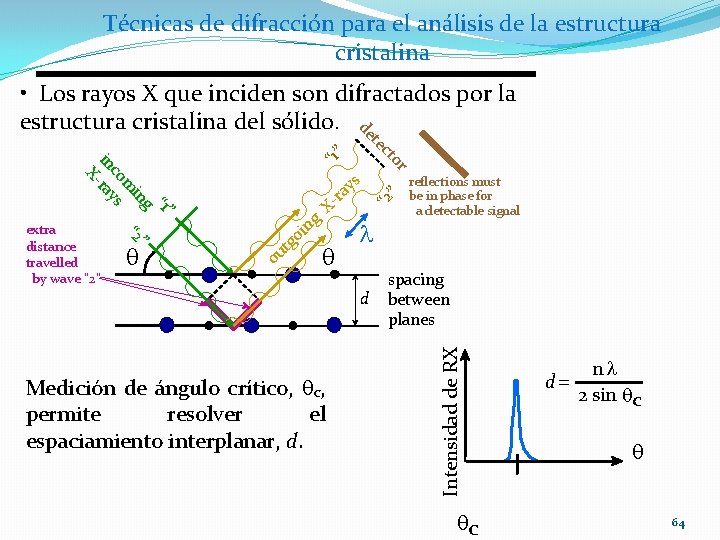
Técnicas de difracción para el análisis de la estructura cristalina • Los rayos X que inciden son difractados por la estructura cristalina del sólido. det q X g n oi o g ut q “ 2 ” s ay r - l d Medición de ángulo crítico, qc, permite resolver el espaciamiento interplanar, d. r reflections must be in phase for a detectable signal spacing between planes Intensidad de RX “ 1” g ” in “ 2 m co s in -ray X extra distance travelled by wave “ 2” ec to qc d = nl 2 sin qc q 64

X-Ray diffractometer Figure 3. 44 Photograph of a XRD diffractometer. (Courtesy of H&M Analytical Services. )

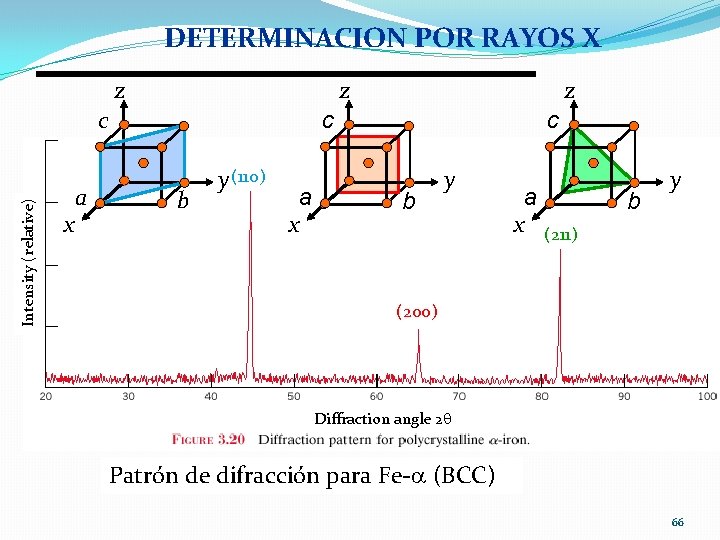
DETERMINACION POR RAYOS X z z Intensity (relative) c x a z c b y (110) a x c b y a x (211) b y (200) Diffraction angle 2 q Patrón de difracción para Fe- (BCC) 66

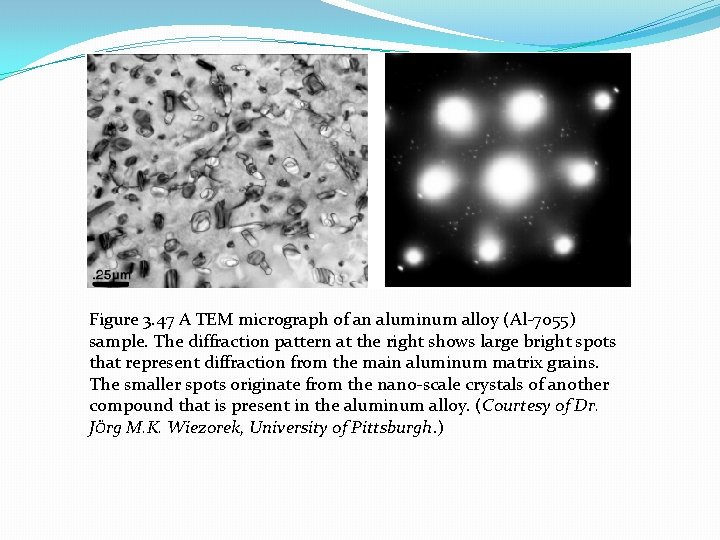
Figure 3. 47 A TEM micrograph of an aluminum alloy (Al-7055) sample. The diffraction pattern at the right shows large bright spots that represent diffraction from the main aluminum matrix grains. The smaller spots originate from the nano-scale crystals of another compound that is present in the aluminum alloy. (Courtesy of Dr. JÖrg M. K. Wiezorek, University of Pittsburgh. )

Tarea (c) 2003 Brooks/Cole Publishing / Thomson Learning 1) Determine los índices de Miller para las direcciones en la celda unitaria cúbica de la Fig.

(c) 2003 Brooks/Cole Publishing / Thomson Learning 2) Determine los índices para los planos en la celda unitaria cúbica de la figura.

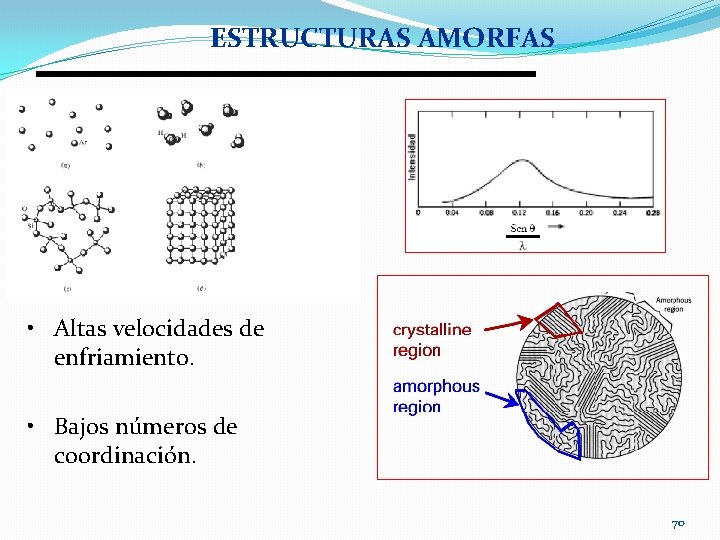
ESTRUCTURAS AMORFAS • Altas velocidades de enfriamiento. • Bajos números de coordinación. 70