Clase 19 Proporcionalidad directa e inversa Objetivo Modelar

Clase 19: Proporcionalidad directa e inversa. Objetivo: Modelar situaciones que involucren proporcionalidad directa o inversa. OA 8 Séptimo básico 2020 Colegio Antupirén. Profesor Jaime Soto A. Semana del 13 al 17 de julio.

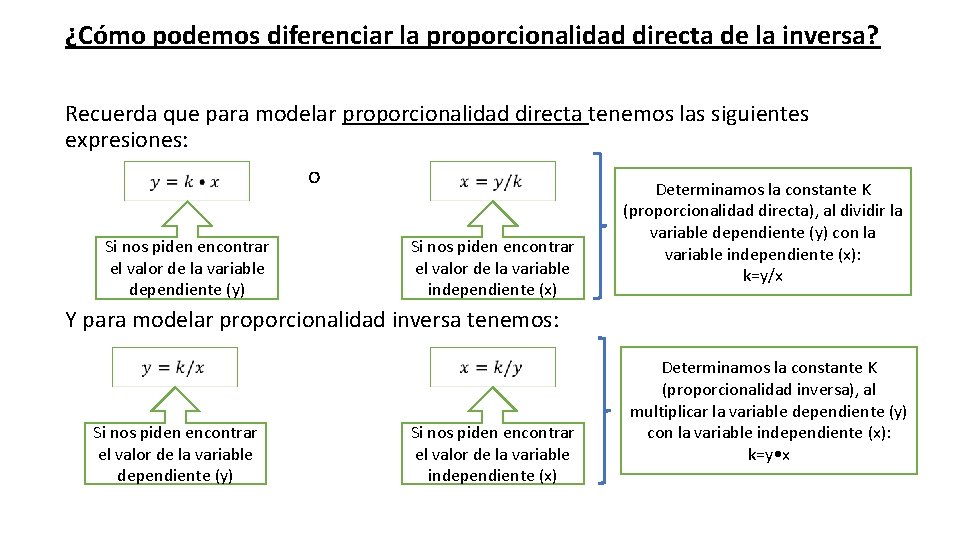
¿Cómo podemos diferenciar la proporcionalidad directa de la inversa? Recuerda que para modelar proporcionalidad directa tenemos las siguientes expresiones: o Determinamos la constante K Si nos piden encontrar el valor de la variable dependiente (y) Si nos piden encontrar el valor de la variable independiente (x) (proporcionalidad directa), al dividir la variable dependiente (y) con la variable independiente (x): k=y/x Y para modelar proporcionalidad inversa tenemos: Si nos piden encontrar el valor de la variable dependiente (y) Si nos piden encontrar el valor de la variable independiente (x) Determinamos la constante K (proporcionalidad inversa), al multiplicar la variable dependiente (y) con la variable independiente (x): k=y • x

Ejemplo: Determina cuál de los siguientes grupos de datos corresponden a una proporcionalidad directa, una proporcionalidad inversa o no es proporcional. (Para esto, debes determinar la constante de proporcionalidad, con todos los valores de las variables de cada tabla. Si al dividir la variable “y” con la variable “x”, en todos los casos dan el mismo valor, es proporcionalidad directa. Si multiplicamos la variable “y” con la variable “x” correspondientemente, y en todos los casos resulta el mismo valor, entonces es proporcionalidad inversa. Si no ocurre nada de lo anterior, entonces no son proporcionales. ) a) c) x y 5 15 1, 5 4, 5 12 36 x y 2 12 6 4 5 4, 8 En este caso, si dividimos los valores de la columna “y”, con los valores de la columna “x”, obtendremos la constante k=3. Por lo tanto, los datos corresponden a una proporcionalidad directa. En este caso, si multiplicamos los valores de la columna “y”, con los valores de la columna “x”, obtendremos la constante k=24. Por lo tanto, los datos corresponden a una proporcionalidad inversa. b) d) x y 8 2 2, 5 10 7 28 x y 5 40 1, 2 9, 6 2, 25 18 En este caso, al dividir o multiplicar los valores de la columna “y” con los valores de la columna “x”, no obtendremos constante alguna. Por lo tanto, los datos no son proporcionales. En este caso, si dividimos los valores de la columna “y”, con los valores de la columna “x”, obtendremos la constante k=8. Por lo tanto, los datos corresponden a una proporcionalidad directa.

Resolución de problemas con proporcionalidad. Para resolver problemas de contexto cotidiano, debemos utilizar las expresiones correspondientes a cada tipo de proporcionalidad. Además de identificar las variables dependientes e independientes. Ejemplo 1: Mario tiene contratado un plan telefónico donde por cada minuto que habla le cobran cierta cantidad de dinero. Si en el mes de junio tiene que pagar un total de $8. 500 por haber utilizado 34 minutos, ¿Cuánto le cobran por cada minuto utilizado? Solución: Primero, determinamos que tipo de proporcionalidad es. A medida que va aumentando la cantidad de minutos utilizado, deberá pagar más (Una variable sube y la otra también). Por lo tanto, hablamos de una proporcionalidad directa. Luego, las variables. La cantidad a pagar depende de cuantos minutos se utilizan. Entonces: Variable independiente “x” Cantidad de minutos utilizados. Variable dependiente “y” Cantidad de dinero a pagar.

Nos piden determinar cual es el valor en pesos (variable “y”) que corresponde a un minuto (variable “x”), entonces tendremos que utilizar la expresión de proporcionalidad directa: Recuerda que, la constante k en una proporcionalidad directa la obtenemos al dividir la variable “y” por la variable “x”. Entonces: y : x = k 8500 : 34 = 250 Ahora, como nos piden saber lo que se paga por 1 minuto, reemplazamos X=1 en la expresión inicial, al igual que k=250 y= 250 • 1 y=250 Por lo tanto, cada minuto del plan cuesta $250.

Ejemplo 2: Una máquina puede estampar 120 folletos en 5 minutos. ¿En cuántos minutos podrá estampar esta máquina 900 folletos? Solución: Determinamos tipo de proporcionalidad. Sabemos que a medida que avanza el tiempo se van estampando más folletos, por lo tanto, hablamos de proporcionalidad directa. Definimos variables: La cantidad de folletos estampados depende del tiempo que funcione la máquina. Variable dependiente “y” cantidad de folletos estampados. Variable independiente “x” Tiempo (en minutos) que trabaja la máquina. Determinamos constante k = y : x k= 120 : 5 k=24 Como queremos saber la variable minutos, sabiendo que son 900 folletos, usamos: x = 900/24 x=37, 5 Por lo tanto, la máquina demorará 37 minutos y medio en estampar 900 folletos.

Ejemplo 3: Don Héctor quiere comprar una parcela. Un amigo le ofrece un terreno de largo igual a 24 mts y de ancho igual a 10 mts. Héctor le dice que se lo comprará siempre y cuando pueda reducir el largo de este en 4 mts, pero manteniendo la misma cantidad de metros cuadrados del terreno (si disminuimos el largo del rectángulo y queremos mantener el área, debemos aumentar su ancho o viceversa). ¿Cuánto deberá medir, entonces, el ancho del terreno con este cambio que pide don Héctor? Solución: Según lo que dice el paréntesis, ya sabemos que este tipo de proporcionalidad es inversa. Así, determinamos la constante k como: k=x • y. EL área de un rectángulo (asociado a un terreno) se calcula multiplicando el largo por el ancho, de este modo, la constante k pasa a ser el mismo valor del área. k= 24 • 10 k=240. (metros cuadrados, área).

Para modelar una situación con proporcionalidad inversa, utilizamos las expresiones: ó En este caso, como nos piden saber el ancho, que depende del largo que tenga el terreno, establecemos las variables como: Variable dependiente (y): ancho del terreno. Variable independiente (x): Largo del terreno. Usamos entonces: Como nos piden reducir el largo en 4 mts, esto quiere decir que desean un largo de 20 mts en vez de 24 mts. (24 -4=20). Así: x=20 k=240 Reemplazamos: y= 240/20 y=12 Por lo tanto, el largo del terreno al dejarlo con 20 mts, el ancho debe tener 12 mts.

Ejemplo 4: En el colegio Antupirén se está realizando una campaña solidaria, donde cada curso debe aportar una cantidad fija, entre todas las familias, de cierto producto. A un curso de séptimo año se les pidió un aporte de 180 kilogramos de azúcar, obviamente a quienes puedan aportar. Inicialmente, se tenía una cantidad total de 25 familias donde cada una aportaría 7, 2 kg. (así, se mantienen los 180 kg de azúcar). Se agregan 5 familias más de este curso para realizar el aporte, de esta manera, cada familia debe aportar lo mismo manteniendo la cantidad fija de kilogramos de azúcar. a) Identifica las variables, dependientes e independientes de esta situación. b) Determina la cantidad en kilogramos de azúcar que debe aportar cada familia a este acto de beneficencia si se agregan estas 5 familias al aporte. Solución: Debemos entender en primer lugar el tipo de proporcionalidad a que apunta el problema. Si la cantidad de familias que aporta aumenta, la cantidad que debe aportar cada una para mantener los 180 kg de azúcar tendrá que disminuir. Por lo tanto, la situación se puede modelar a través de una proporcionalidad inversa.

Para identificar las variables, hacemos el ejercicio mental de establecer cuál depende una de la otra. En este caso, la cantidad de azúcar que aporta cada familia dependerá de la cantidad de familias que colaboren. (Respuesta de a) Variable dependiente (y): Cantidad de azúcar (en kg) que aporta cada familia. Variable independiente (x): Cantidad de familias que aporten a la causa. Utilizamos la expresión La constante k=180 (la cantidad fija de azúcar en kg) Como nos indicaron en el problema, a las 25 familias iniciales se agregan 5 más, dando un total de 30 familias que harán el aporte voluntario. De esta forma, la variable X es igual a 30. Reemplazamos: y= 180/30 y=6 (Respuesta de b): Al agregar 5 familias para el aporte, cada una tendrá que aportar entonces 6 kg de azúcar.