Claims claims and more claims The work of























- Slides: 29

Claims, claims and more claims? The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 1

The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 2

The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 3

The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 4

The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 5

Some questions? • Does 1 in 6 instantly win? • Is 1 in 6 the average odds? • What does this means? The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 6

So off the shop I went and purchased 18 bars. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 7

The shop keeper, on seeing the 18 bars, says to me: “Wow man, you gonna win three free ones!” “I have a friend who knows how to tell if they are a winner – he got 9 in a row. But he will not tell me his secret!” The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 8

What do you think the result was? Please write down what you think? The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 9

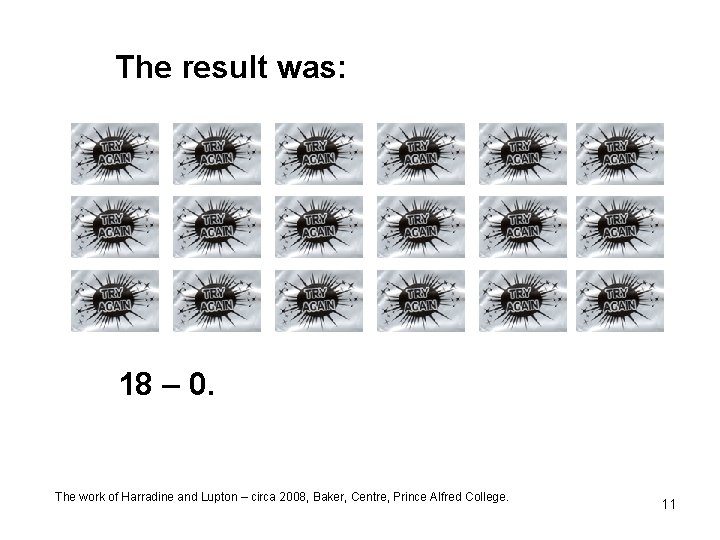
The result was: The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 10

The result was: 18 – 0. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 11

Some more questions. Does 18 – 0 shock you? Is there really 1 in 6 winners? Could the bloke really have got 9 winners in a row, or is he a liar? The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 12

How to answer? What would be the most ‘natural’ way? Natural to who? • First you. • Now your students. Please write down what you think. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 13

How to answer (for you)? A binomial probability calculation? (or should that be a hyper-geometric? ) Use exact binomial inference? (or did you choose differently? ) (This ‘sort of natural’ is often why this sort of problem is not considered suitable for young students. ) The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 14

How to answer (for the students)? Buy lots of sets of 18 – see how this process behaves. But is this realistic? The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 15

Simulate! But how? Suggestions please. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 16

Manual sampling. Required until the kids get a sound understanding of what they are doing. That is – they are producing the COULD HAVE BEENS (sets of 18). Rossman and Harradine, IASE RT 2008. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 17

Let’s do the same thing, electronically – but how many times? Lots! The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. BINPOP – makes a box (population) of 999 zeros/ones with the proportion of ones of your choice and puts them in File 2 List 1. SEESAMPS – chooses 5 SRSs of size of your choice from File 2 List 1 and places then in File 2 Lists 2 - 6. REPSAMPR – repeatedly draws SRSs from File 2 List 1. You choose how many and what size (n). Only the p-hat is reported and they are not stored anywhere. SEEPROPS – acts like REPSAMPR, but stores the results in File 2 List 2. Be patient for big jobs. 18

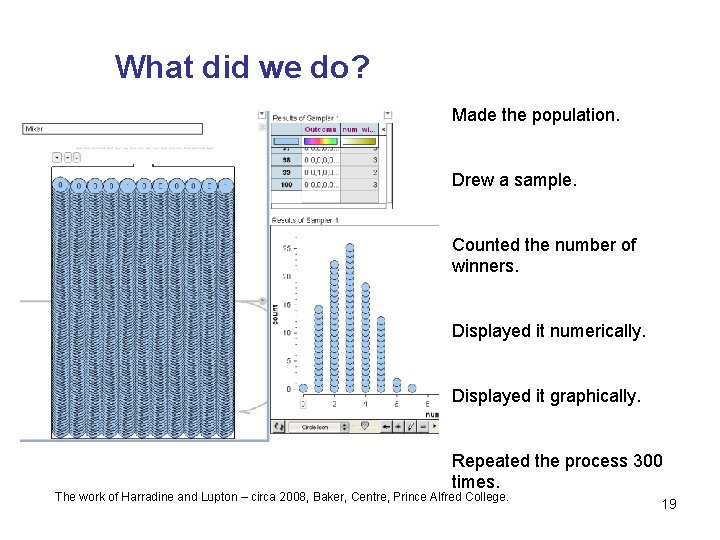
What did we do? Made the population. Drew a sample. Counted the number of winners. Displayed it numerically. Displayed it graphically. Repeated the process 300 times. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 19

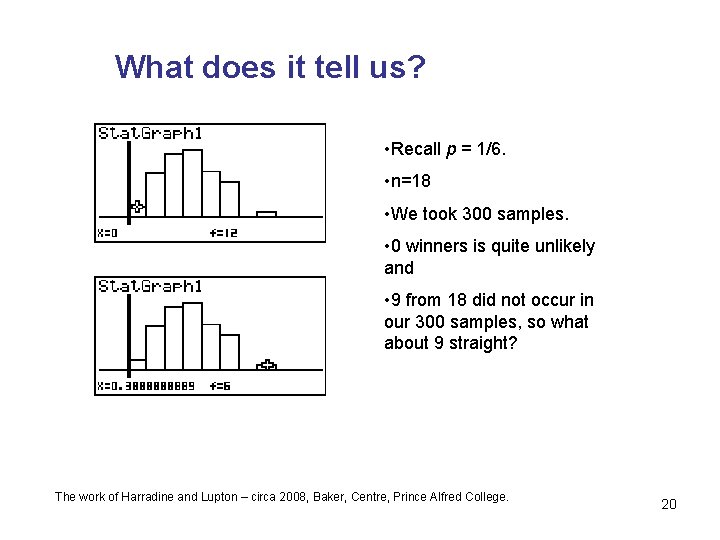
What does it tell us? • Recall p = 1/6. • n=18 • We took 300 samples. • 0 winners is quite unlikely and • 9 from 18 did not occur in our 300 samples, so what about 9 straight? The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 20

What if we did not buy 18? What if the claim was not 1 in 6? Is there any predictability to the sampling process? Let’s study the process some. How? Suggestions please. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 21

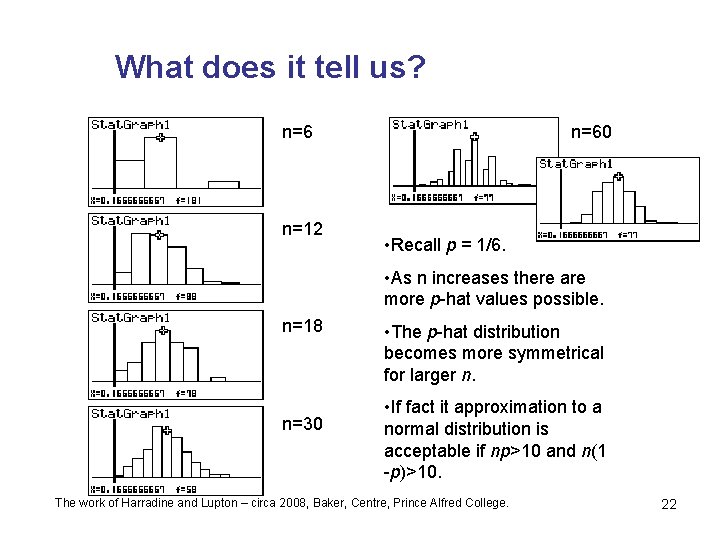
What does it tell us? n=60 n=6 n=12 • Recall p = 1/6. • As n increases there are more p-hat values possible. n=18 n=30 • The p-hat distribution becomes more symmetrical for larger n. • If fact it approximation to a normal distribution is acceptable if np>10 and n(1 -p)>10. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 22

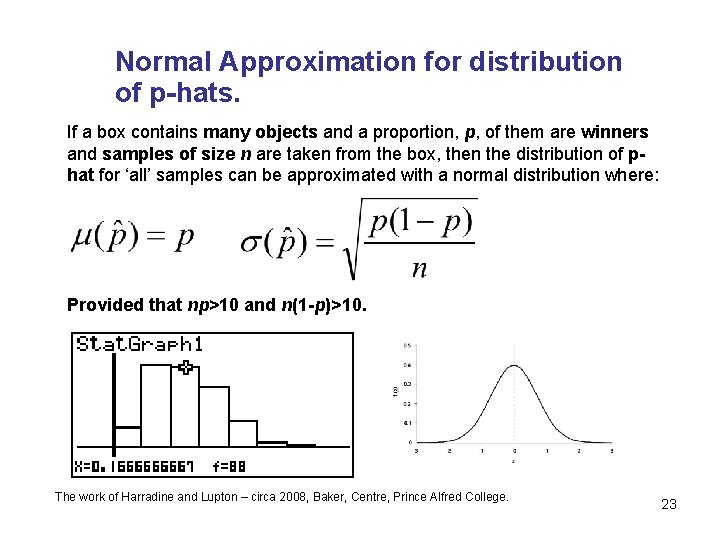
Normal Approximation for distribution of p-hats. If a box contains many objects and a proportion, p, of them are winners and samples of size n are taken from the box, then the distribution of phat for ‘all’ samples can be approximated with a normal distribution where: Provided that np>10 and n(1 -p)>10. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 23

Now lets draw some normal approximations to p-hat distributions. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 24

Where are the rare bits? The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 25

CSI – claim scene investigation? In pairs please: • One person make a box (population) with a p of your choosing – use BINPOP. • That same person then makes a claim about the p of the population in list 1. You can be truthful or lie (a bit or a lot). • The other person then is allowed to take ONE sample of a size of their choosing (use REPSAMPR) – and determine if it is in the rare zone and from that make a conclusion. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 26

CSI – claim scene investigation? So now it is my turn to be the maker! I will take two shots. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 27

Let’s get formal! H 0 : p = 0. 4 HA : p 0. 4 N(0, 1) Test Statistic (Z) = -2. 04 p-value = p(Z -2. 04) + p(Z 2. 04) = 0. 041 ( 0. 05) we reject the null hypothesis Alternatively Z = -2. 04 and since -2. 12 < -1. 96 we reject H 0. We can conclude that the percentage of winners is different to 40%. The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 28

Well if it is not what is claimed, then what is it? The case of the almost worst case scenario. (done on the whiteboard). The work of Harradine and Lupton – circa 2008, Baker, Centre, Prince Alfred College. 29
 Lirik lagu more more more we praise you
Lirik lagu more more more we praise you More more more i want more more more more we praise you
More more more i want more more more more we praise you Human history becomes more and more a race
Human history becomes more and more a race You should not open a persuasive request with a question.
You should not open a persuasive request with a question. A researcher claims that 62 of voters favor gun control
A researcher claims that 62 of voters favor gun control 5 apples in a basket riddle
5 apples in a basket riddle The more you study the more you learn
The more you study the more you learn Aspire not to have more but to be more
Aspire not to have more but to be more More mass more inertia
More mass more inertia Knowing more remembering more
Knowing more remembering more More love to thee o lord
More love to thee o lord More choices more chances
More choices more chances Chapter 4 section 1 work and machines answer key
Chapter 4 section 1 work and machines answer key Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Gấu đi như thế nào
Gấu đi như thế nào Thang điểm glasgow
Thang điểm glasgow Alleluia hat len nguoi oi
Alleluia hat len nguoi oi Môn thể thao bắt đầu bằng chữ đua
Môn thể thao bắt đầu bằng chữ đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công của trọng lực
Công của trọng lực Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Phép trừ bù
Phép trừ bù Phản ứng thế ankan
Phản ứng thế ankan Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật