CIT 383 Administrative Scripting Numbers Computer Security Art

CIT 383: Administrative Scripting Numbers Computer Security: Art and Science 1

Types of Numbers Integers § Numbers without decimal points. § -3, 0, 2, 65536 § Precise operations. § 1+2=3 § 1 – 2 = -1 § 1*2=2 § 1/2 =0 CIT 383: Administrative Scripting Floats § Numbers with decimal points. § -199. 9482, 0. 0, 3. 14 § Rounding errors. § 1. 0 + 2. 0 = 3. 0 § 1. 0 – 2. 0 = -1. 0 § 1. 0 * 2. 0 = 2. 0 § 1. 0 / 2. 0 = 0. 5

Why Two Types of Numbers? Different uses – Money calculations should avoid rounding. – Measurements must often be floats. Performance – Floats take more space than integers. (usually) – CPU has separate integer and float units. CIT 383: Administrative Scripting

Computer Security: Art and Science 4

Two Types of Integers Fixnum – 32 -bit machine integer – Fast (calculations in hardware) – Ranges from -231 to 231 – Ruby promotes to Bignum beyond range. Bignum – Arbitrary precision integer – Slow (calculations in software) – No limit to size. CIT 383: Administrative Scripting
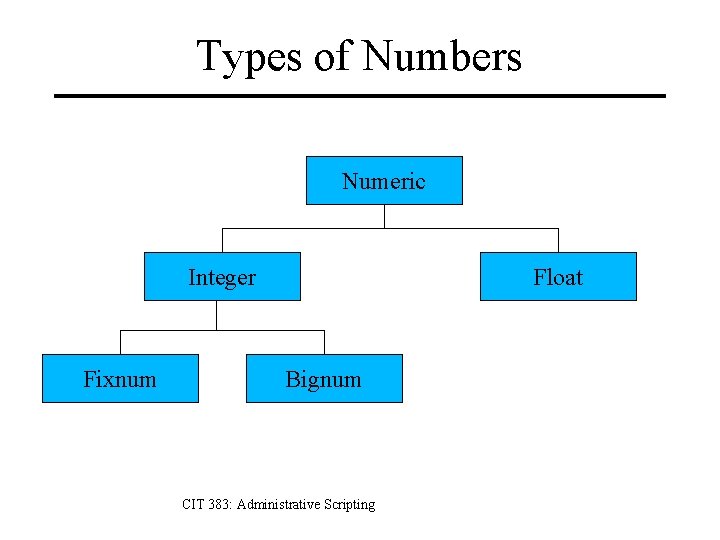
Types of Numbers Numeric Integer Fixnum Float Bignum CIT 383: Administrative Scripting

Integer Literals Different bases Decimal: 255 Octal: 0377 Binary: 0 b 1111 Hexadecimal: 0 x. FF Readability Insert _ as thousands separator. Can write 100000 as 1_000_000 CIT 383: Administrative Scripting

Float Literals Always need a decimal point 1 is an integer, 1. 0 is a float Scientific notation Avogadro’s number is 6. 0221415 e 23 Readability 1_000_000. 0 CIT 383: Administrative Scripting

Arithmetic Operators Addition: + 7 + 3 == 10 Subtraction: 7 – 3 == 4 Multiplication: * 7 * 3 == 21 Division: / 13 % 2 == 6 Remainder: % 13 % 2 == 1 Exponentiation: ** 2**8 == 256 CIT 383: Administrative Scripting

Logical Operations Return a true or false value. Equality 1 == 1 Inequality 1 != 1 Less Than 1<2 Greater Than 1>2 Less Than or Equal To 1 >= 2 Greater Than or Equal To 1 <= 1 CIT 383: Administrative Scripting

Floating Point Rounding Machine floats – Stored as binary fractions: ½, ¼, etc. – Decimal fractions: 0. 1 cannot be exactly represented, as it’s repeating in binary like 1/3. Don’t use equality tests for floats 0. 4 – 0. 3 == 0. 1 is false Check if difference is sufficiently small (0. 4 – 0. 3) – 0. 1 < 1. 0 e-9 is true CIT 383: Administrative Scripting

Variables allow us to name values x = 1. 0 x # Assigns the value 1. 0 to x # A variable reference, evals to 1. 0 Variable naming – Valid characters: letters, numbers, _ – Name must start with letter or _ – Case sensitive: now, no. W, n. Ow are different – If name starts with capital, it is a constant. – Examples: x, y 2, new_val, _secret, PI CIT 383: Administrative Scripting

References 1. Michael Fitzgerald, Learning Ruby, O’Reilly, 2008. 2. David Flanagan and Yukihiro Matsumoto, The Ruby Programming Language, O’Reilly, 2008. 3. Hal Fulton, The Ruby Way, 2 nd edition, Addison-Wesley, 2007. 4. Dave Thomas with Chad Fowler and Andy Hunt, Programming Ruby, 2 nd edition, Pragmatic Programmers, 2005. Computer Security: Art and Science 13
- Slides: 13