CISE 301 Numerical Methods Topic 8 Ordinary Differential

CISE 301: Numerical Methods Topic 8 Ordinary Differential Equations (ODEs) Lecture 28 -36 KFUPM (Term 101) Section 04 Read 25. 1 -25. 4, 26 -2, 27 -1 CISE 301_Topic 8 L 7 1

Outline of Topic 8 Lesson 1: Introduction to ODEs p Lesson 2: Taylor series methods p Lesson 3: Midpoint and Heun’s method p Lessons 4 -5: Runge-Kutta methods p Lesson 6: Solving systems of ODEs p Lesson 7: Multiple step Methods p Lesson 8 -9: Boundary value Problems p CISE 301_Topic 8 L 7 2

Lecture 34 Lesson 7: Multiple Step Methods CISE 301_Topic 8 L 7 3

Outlines of Lesson 7 Solution of ODEs Lesson 7: Adam-Moulton Multi-step Predictor-Corrector Methods CISE 301_Topic 8 L 7 4

Learning Objectives of Lesson 7 p Appreciate the importance of multi-step methods. p Discuss advantages/disadvantages of multi -step methods. p Solve first order ODEs using Adams Moulton multi-step method. CISE 301_Topic 8 L 7 5

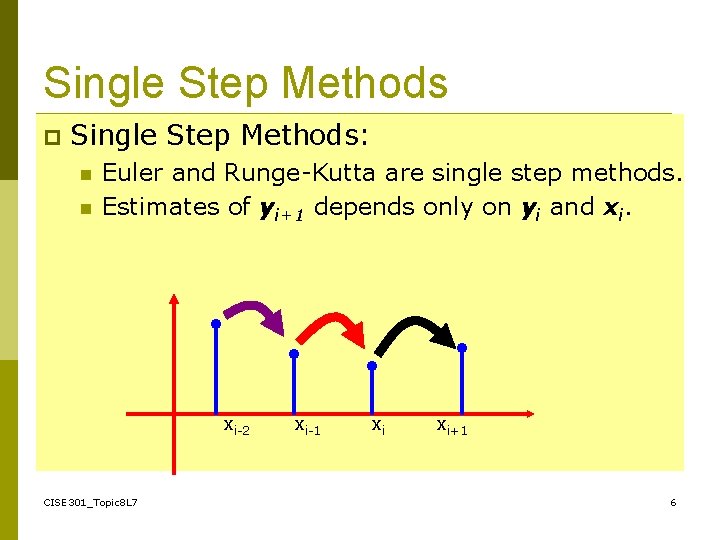
Single Step Methods p Single Step Methods: n n Euler and Runge-Kutta are single step methods. Estimates of yi+1 depends only on yi and xi. xi-2 CISE 301_Topic 8 L 7 xi-1 xi xi+1 6

Multi-Step Methods p 2 -Step Methods n In a two-step method, estimates of yi+1 depends on yi, yi-1, xi, and xi-1 xi-2 CISE 301_Topic 8 L 7 xi-1 xi xi+1 7

Multi-Step Methods p 3 -Step Methods n In an 3 -step method, estimates of yi+1 depends on yi , yi-1 , yi-2, xi-1, and xi-2 CISE 301_Topic 8 L 7 xi-1 xi xi+1 8

Heun’s Predictor Corrector Method Heun’s predictor corrector method is not a multi-step method. CISE 301_Topic 8 L 7 9

2 -Step Predictor-Corrector • At each iteration one prediction step is done and as many correction steps as needed. • is the estimate of the solution at xi+1 after k correction steps. CISE 301_Topic 8 L 7 10

3 -Step Predictor-Corrector CISE 301_Topic 8 L 7 11

4 -Step Adams-Moulton Predictor. Corrector CISE 301_Topic 8 L 7 12

How Many Function Evaluations are Done? Number of function evaluations is the Computational Speed or Efficiency How many evaluations per step? No need to repeat the evaluation of function f at previous points Only one new function evaluation in the predictor One function evaluation per correction step # of function evaluations = 1+ number of corrections CISE 301_Topic 8 L 7 13

Example CISE 301_Topic 8 L 7 14

Example CISE 301_Topic 8 L 7 15

Example CISE 301_Topic 8 L 7 16

Multi-Step Methods p Single Step Methods n n p Euler and Runge-Kutta are single step methods. Information about y(x) is used to estimate y(x+h). Multistep Methods n n Adam-Moulton method is a multi-step method. To estimate y(x+h), information about y(x), y(x-h), y(x-2 h)… are used. CISE 301_Topic 8 L 7 17

Number of Steps p At each iteration, one prediction step is done and as many correction steps as needed. p Usually few corrections are done (1 to 3). p It is usually better (in terms of accuracy) to use smaller step size than corrections. CISE 301_Topic 8 L 7 18