CIS 750 Seminar in Advanced Topics in Computer

General Overview n Multimedia Indexing n Spatial Access Methods (SAMs) n n n k-d

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d

Spatial Access Methods - problem n n Given a collection of geometric objects (points,

SAMs - motivation traditional DB age salary GIS

SAMs - motivation CAD/CAM find elements too close to each other

SAMs - motivation eg, . std S 1 F(S 1) 1 365 day Sn

SAMs: solutions n n n K-d trees point quadtrees MX-quadtrees z-ordering R-trees (grid files)

k-d trees n n n Used to store k dimensional point data It is

2 -d trees – node structure n n n Binary trees Info: information field

2 -d trees: Insertion/Search n To insert a node N into the tree pointed

2 -d trees – Example of Insertion City (Xval, Yval) Banja Luka (19, 45)

2 -d trees: Deletion n Deletion of point (x, y) from T n n

2 -d trees: Deletion n Finding candidate replacement nodes for deletion n Replacement node

2 -d trees: Range Queries n n Q: Given a point (xc, yc) and

Point Quadtrees n n n Represent point data Always split regions into 4 parts

Point Quadtrees n Nodes in point quadtrees represent regions

Point quadtrees - Insertion City (Xval, Yval) Banja Luka (19, 45) Derventa (40, 50)

Point quadtrees: Deletion n Deletion of point (x, y) from T n n If

Point quadtrees: Range Searches n n Each node in a point quadtree represents a

MX-Quadtrees n Drawbacks of 2 -d trees, point quadtrees: n n n shape of

MX-Quadtrees n n Assumption: the map is represented as a grid of size (2

MX-Quadtrees - Insertion After insertion of A, B, C, and D respectively

MX-Quadtrees - Deletion n Fairly easy – why? All point are represented at the

MX-Quadtrees –Range Queries n n Same as in point quadtrees One difference: n Checking

z-ordering Q: how would you organize, e. g. , n-dim points, on disk? (C

z-ordering Q 2: how? A: assume finite granularity; z-ordering = bit-shuffling = N-trees =

z-ordering Q 2: how? A: assume finite granularity (e. g. , 232 x 232

z-ordering Q 2. 1: how to map n-d cells to 1 -d cells?

z-ordering Q 2. 1: how to map n-d cells to 1 -d cells? A:

z-ordering Q: is it good? A: great for ‘x’ axis; bad for ‘y’ axis

z-ordering Q: How about the ‘snake’ curve?

z-ordering Q: How about the ‘snake’ curve? A: still problems: 2^32

z-ordering Q: Why are those curves ‘bad’? A: no distance preservation (~ clustering) Q:

z-ordering Q: solution? (w/ good clustering, and easy to compute, for 2 -d and

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y) )? A: 3

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y))? A 1: ‘z’

$z-ordering Notice: n self similar (we’ll see about fractals, soon) n method is hard$

z-ordering bit-shuffling x 00 y 11 10 01 00 y 11 z =( 0

z-ordering linear-quadtrees : assign N->1, S->0 e. t. c. W E 1 0 0

z-ordering. . . and repeat recursively. Eg. : zgray-cell = WN; WN = (0101)2

z-ordering Drill: z-value of grey cell, with the three methods? W E 1 N

z-ordering - Detailed outline n spatial access methods n z-ordering n n n main

z-ordering - usage & algo’s Q 1: How to store on disk? A: Q

z-ordering - usage & algo’s Q 1: How to store on disk? A: treat

z-ordering - usage & algo’s MAJOR ADVANTAGES w/ B-tree: n already inside commercial systems

z-ordering - usage & algo’s Q 2: queries? (eg. : find city at (0,

z-ordering - usage & algo’s Q 2: range queries? PGH SF

z-ordering - usage & algo’s Q 2: range queries? A: compute ranges of z-values;

z-ordering - usage & algo’s Q 2’: range queries - how to reduce #

z-ordering - usage & algo’s Q 2’’: range queries - how to break a

z-ordering - usage & algo’s Q 3: k-nn queries? (say, 1 -nn)? PGH SF

z-ordering - usage & algo’s Q 3: k-nn queries? (say, 1 -nn)? A: traverse

z-ordering - usage & algo’s. . . ask a range query. PGH SF nn

z-ordering - usage & algo’s Q 4: all-pairs queries? ( all pairs of cities

z-ordering - regions Q: z-value for a region? B A C z. B =

z-ordering - regions Q: z-value for a region? A: 1 or more z-values; by

z-ordering - regions “don’t care” Q: z-value for a region? W E A 1

z-ordering - regions Q: How to store in B-tree? Q: How to search (range

z-ordering - regions Q: How to store in B-tree? A: sort (*<0<1) Q: How

z-ordering - regions Q: How to search (range etc queries) – eg ‘red’ range

z-ordering - regions Almost identical to range queries for point data, except for the

z-ordering - regions z 1= 1100 ? ? 11** = z 2 Specifically: does

z-ordering - regions n n r 2 will either contain completely, or avoid completely

z-ordering - regions Drill (True/False). Given: n z 1= 011001** n z 2= 01******

z-ordering - regions Drill (True/False). Given: n z 1= 011001** z 2 n z

z-ordering - regions Spatial joins: find (quickly) all counties intersecting lakes

z-ordering - regions Spatial joins: find (quickly) all counties intersecting Naive algorithm: O( N

z-ordering - regions Spatial joins: find (quickly) all counties intersecting lakes Solution: merge the

z-ordering - variations Q: is z-ordering the best we can do?

z-ordering - variations Q: is z-ordering the best we can do? A: probably not

z-ordering - variations A 2: Hilbert curve! (a. k. a. Hilbert-Peano curve)

z-ordering - variations ‘Looks’ better (never long jumps). How to derive it?

z-ordering - variations ‘Looks’ better (never long jumps). How to derive it? order-1 order-2

z-ordering - variations Q: function for the Hilbert curve ( h = f(x, y)

z-ordering - variations Q: how about Hilbert curve in 3 -d? n-d? A: Exists

z-ordering - analysis Q: How many pieces (‘quad-tree blocks’) per region? A: proportional to

z-ordering - analysis (How long is the coastline, say, of England? Paradox: The answer

z-ordering - analysis Q: Should we decompose a region to full detail (and store

z-ordering - analysis Q: how to measure the ‘goodness’ of a curve?

z-ordering - analysis Q: how to measure the ‘goodness’ of a curve? A: e.

z-ordering - analysis Q: So, is Hilbert really better? A: 27% fewer runs, for

z-ordering - fun observations Hilbert and z-ordering curves: “space filling curves”: eventually, they visit

z-ordering - fun observations. . . they show that the plane has as many

z-ordering - fun observations Observation #2: Hilbert (like) curve for video encoding [Y. Matias+,

z-ordering - fun observations In general, Hilbert curve is great for preserving distances, clustering,

Conclusions n n n z-ordering is a great idea (n-d points -> 1 -d

Slides: 128

Download presentation

CIS 750 – Seminar in Advanced Topics in Computer Science Advanced topics in databases – Multimedia Databases V. Megalooikonomou Spatial Access Methods (SAMs) I (some slides are based on notes by C. Faloutsos)

General Overview n Multimedia Indexing n Spatial Access Methods (SAMs) n n n k-d trees Point Quadtrees MX-Quadtree z-ordering R-trees

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

Spatial Access Methods - problem n n Given a collection of geometric objects (points, lines, polygons, . . . ) organize them on disk, to answer spatial queries (like? ? )

Spatial Access Methods - problem n n Given a collection of geometric objects (points, lines, polygons, . . . ) organize them on disk, to answer n n point queries range queries k-nn queries spatial joins (‘all pairs’ queries)

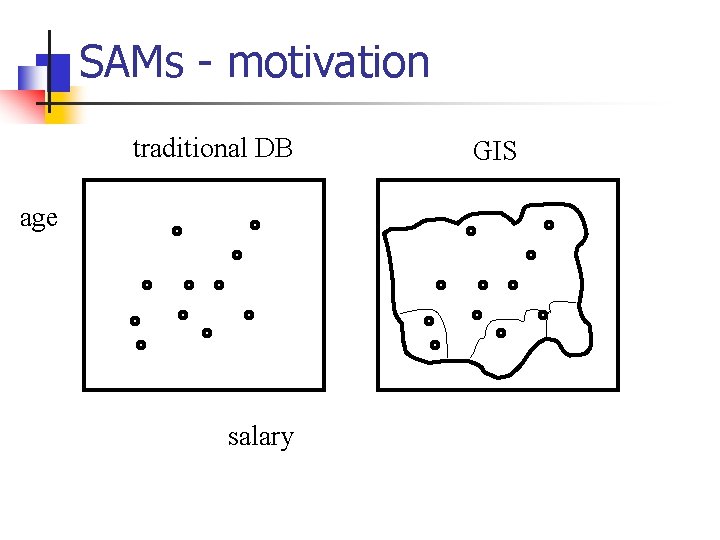
SAMs - motivation n Q: applications?

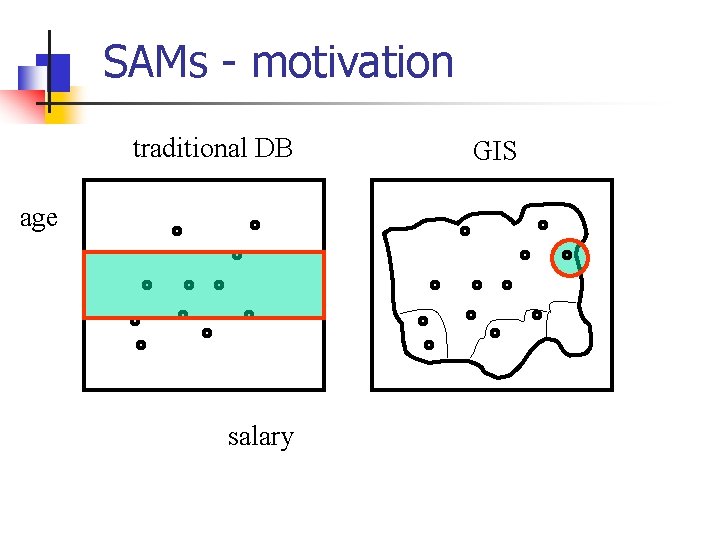
SAMs - motivation traditional DB age salary GIS

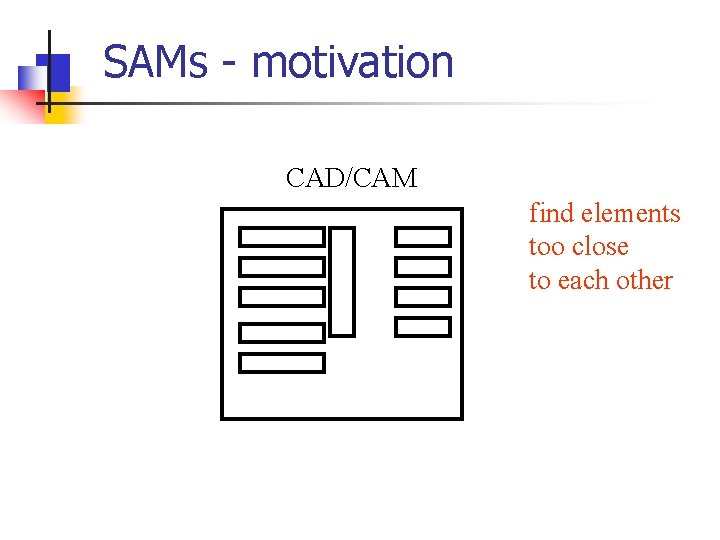
SAMs - motivation CAD/CAM find elements too close to each other

SAMs - motivation CAD/CAM

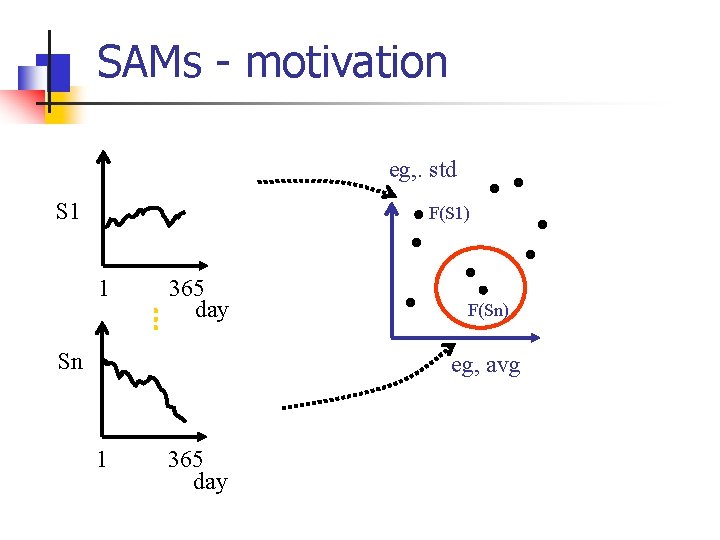
SAMs - motivation eg, . std S 1 F(S 1) 1 365 day Sn F(Sn) eg, avg 1 365 day

SAMs: solutions n n n K-d trees point quadtrees MX-quadtrees z-ordering R-trees (grid files) Q: how would you organize, e. g. , n-dim points, on disk? (C points per disk page)

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

k-d trees n n n Used to store k dimensional point data It is not used to store region data A 2 -d tree (i. e. , for k=2) stores 2 dimensional point data while a 3 -d tree stores 3 -dimensional point data, etc.

2 -d trees – node structure n n n Binary trees Info: information field Xval, Yval: coordinates of a point associated with the node Llink, Rlink: pointers to children Properties (N: node): n If level N even -> n n n for all nodes M in the subtree rooted at N. Llink: M. Xval < N. Xval for all nodes P in the subtree rooted at N. Rlink: P. Xval >= N. Xval If level N odd -> n Similarly use Yvals

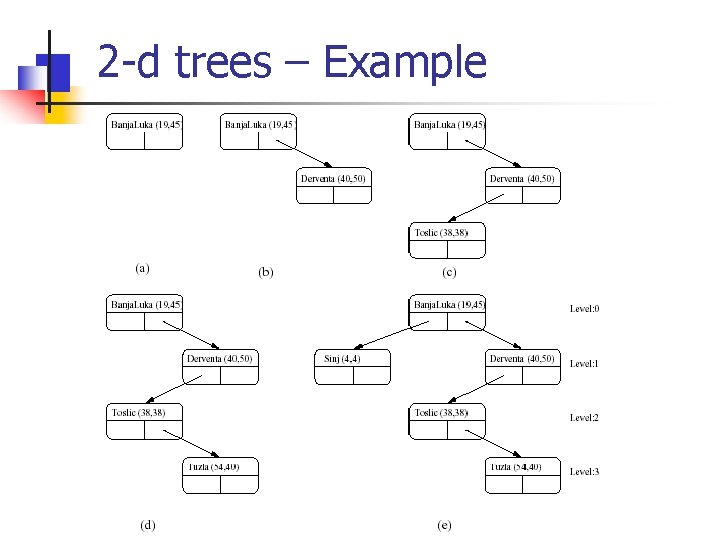
2 -d trees – Example

2 -d trees: Insertion/Search n To insert a node N into the tree pointed by T n n n If N and T agree on Xval, Yval then overwrite T Else, branch left if N. Xval < T. xval, right otherwise (even levels) Similarly for odd levels (branching on Yvals)

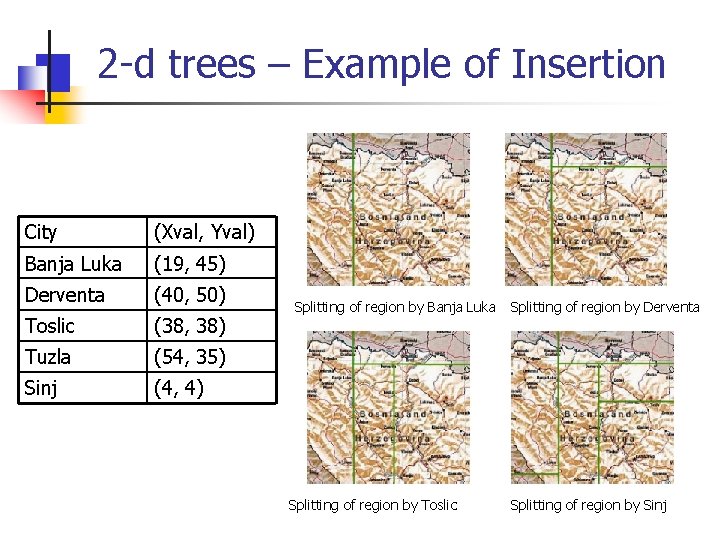
2 -d trees – Example of Insertion City (Xval, Yval) Banja Luka (19, 45) Derventa (40, 50) Toslic (38, 38) Tuzla (54, 35) Sinj (4, 4) Splitting of region by Banja Luka Splitting of region by Toslic Splitting of region by Derventa Splitting of region by Sinj

2 -d trees: Deletion n Deletion of point (x, y) from T n n If N is a leaf node easy Otherwise either Tl (left subtree) or Tr (right subtree) is non-empty n n Find a “candidate replacement” node R in Tl or Tr Replace all of N’s non-link fields by those of R Recursively delete R from Ti Recursion guaranteed to terminate - Why?

2 -d trees: Deletion n Finding candidate replacement nodes for deletion n Replacement node R must bear same spatial relation to all nodes in Tl and Tr as node N

2 -d trees: Range Queries n n Q: Given a point (xc, yc) and a distance r find all points in the 2 -d tree that lie within the circle A: Each node N in a 2 -d tree implicitly represents a region RN – If the circle (specified by the query) has no intersection with RN then there is no point in searching the subtree rooted at node N

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees z-ordering R-trees

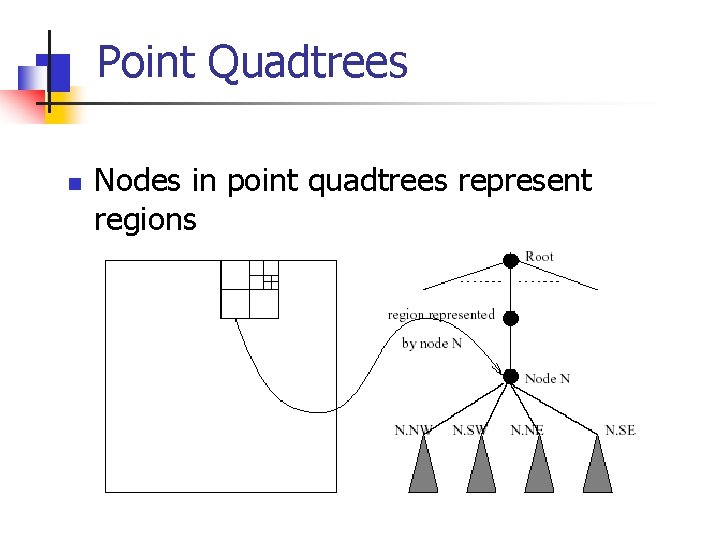
Point Quadtrees n n n Represent point data Always split regions into 4 parts 2 -d tree: a node N splits a region into two by drawing one line through the point (N. xval, N. yval) Point quadtree: a node N splits a region by drawing a horizontal and a vertical line through the point (N. xval, N. yval) Four parts: NW, SW, NE, and SE quadrants Q: Quadtree nodes have 4 children?

Point Quadtrees n Nodes in point quadtrees represent regions

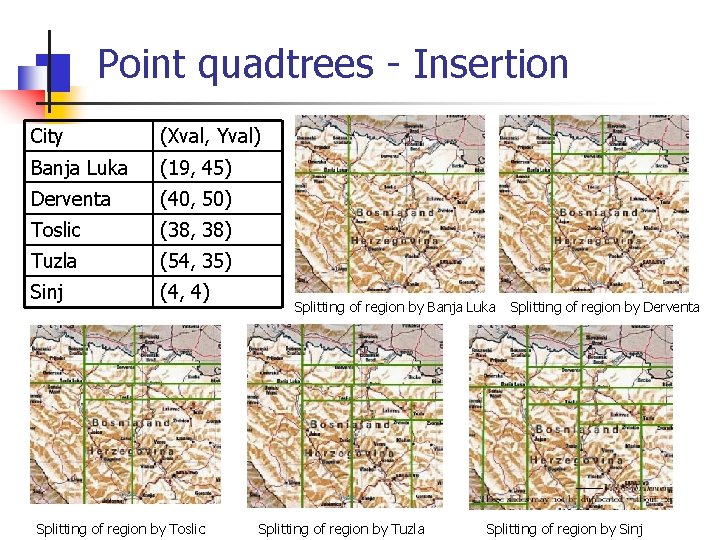
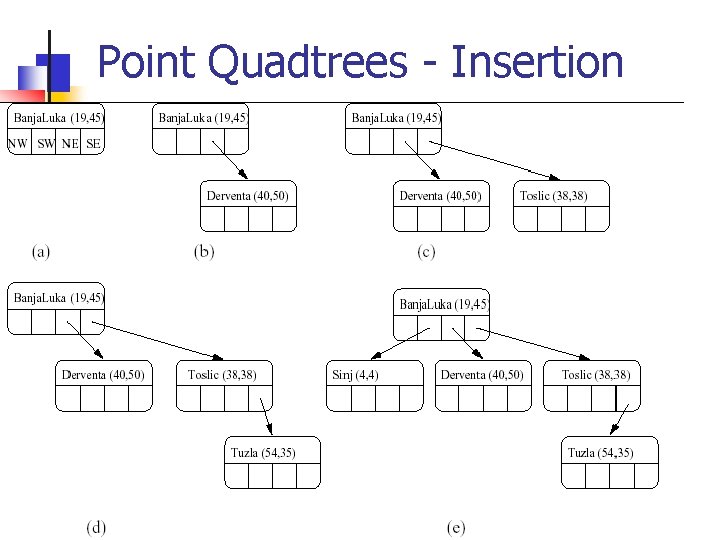
Point quadtrees - Insertion City (Xval, Yval) Banja Luka (19, 45) Derventa (40, 50) Toslic (38, 38) Tuzla (54, 35) Sinj (4, 4) Splitting of region by Toslic Splitting of region by Banja Luka Splitting of region by Tuzla Splitting of region by Derventa Splitting of region by Sinj

Point Quadtrees - Insertion

Point quadtrees: Deletion n Deletion of point (x, y) from T n n If N is a leaf node easy Otherwise a subtree (N. NW, N. SW, N. NE. N. SE) is nonempty n Find a “candidate replacement” node R in one of the subtrees such that: n n n n Every other node R 1 in N. NW is to the NW of R Every other node R 2 in N. SW is to the SW of R etc… Replace all of N’s non-link fields by those of R Recursively delete R from Ti In general, it may not always be possible to find such as replacement node Q: What happens in the worst case?

Point quadtrees: Range Searches n n Each node in a point quadtree represents a region Do not search regions that do not intersect the circle defined by the query

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

MX-Quadtrees n Drawbacks of 2 -d trees, point quadtrees: n n n shape of tree depends upon the order in which objects are inserted into the tree splits may be uneven depending upon where the point (N. xval, N. yval) is located inside the region (represented by N) MX-quadtrees: shape (and height) of tree independent of number of nodes and order of insertion

MX-Quadtrees n n Assumption: the map is represented as a grid of size (2 k x 2 k) for some k When a region gets “split” it splits down the middle

MX-Quadtrees - Insertion After insertion of A, B, C, and D respectively

MX-Quadtrees - Deletion n Fairly easy – why? All point are represented at the leaf level Total time for deletion: O(k)

MX-Quadtrees –Range Queries n n Same as in point quadtrees One difference: n Checking to see if a point is in the circle defined by the range query needs to be performed at the leaf level (points are stored at the leaf level)

SAMs - Detailed outline n spatial access methods n n n problem dfn k-d trees point quadtrees MX-quadtrees z-ordering R-trees

z-ordering Q: how would you organize, e. g. , n-dim points, on disk? (C points per disk page) Hint: reduce the problem to 1 -d points(!!) Q 1: why? A: Q 2: how?

z-ordering Q: how would you organize, e. g. , n-dim points, on disk? (C points per disk page) Hint: reduce the problem to 1 -d points (!!) Q 1: why? A: B-trees! Q 2: how?

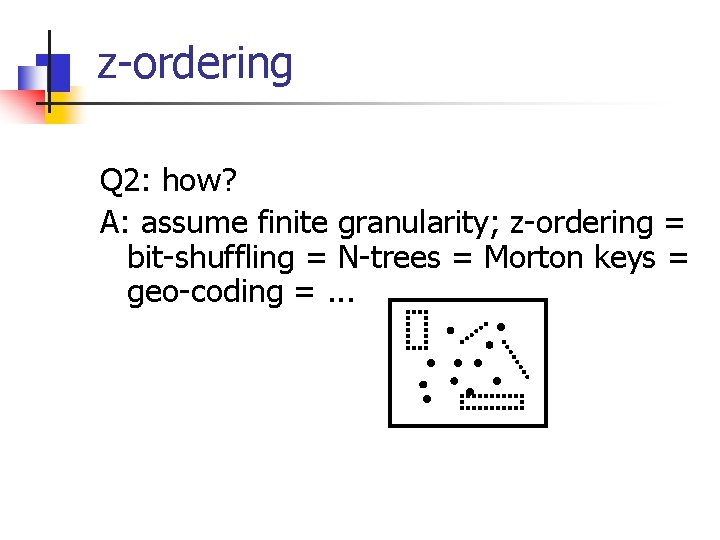
z-ordering Q 2: how? A: assume finite granularity; z-ordering = bit-shuffling = N-trees = Morton keys = geo-coding =. . .

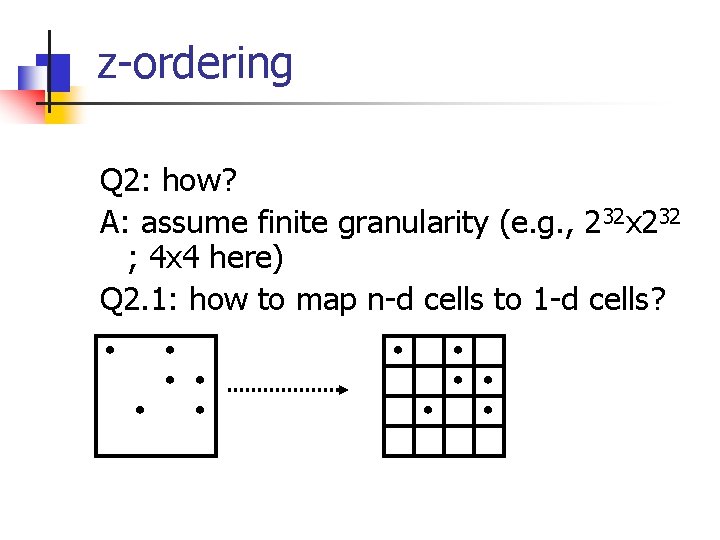
z-ordering Q 2: how? A: assume finite granularity (e. g. , 232 x 232 ; 4 x 4 here) Q 2. 1: how to map n-d cells to 1 -d cells?

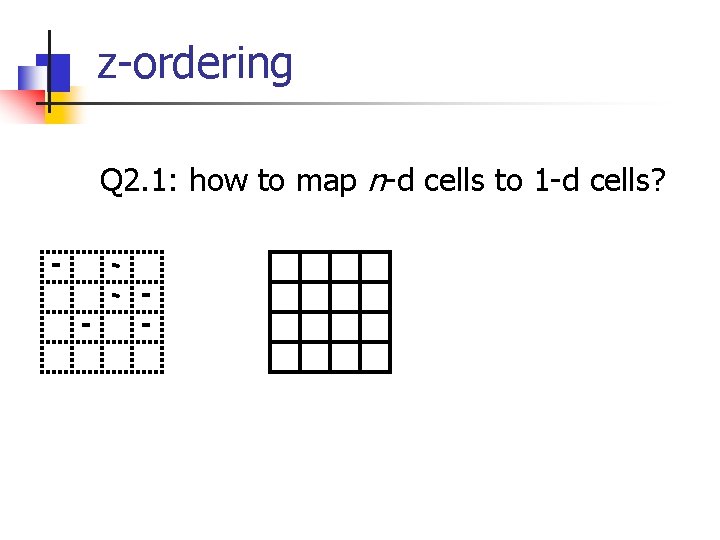
z-ordering Q 2. 1: how to map n-d cells to 1 -d cells?

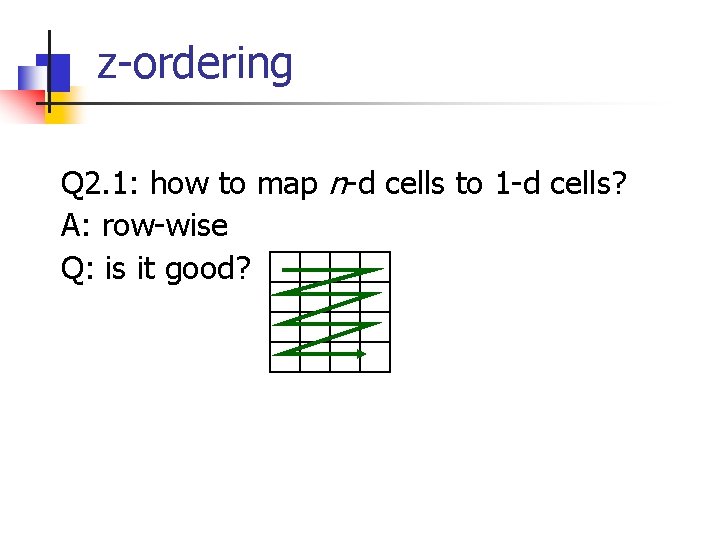
z-ordering Q 2. 1: how to map n-d cells to 1 -d cells? A: row-wise Q: is it good?

z-ordering Q: is it good? A: great for ‘x’ axis; bad for ‘y’ axis

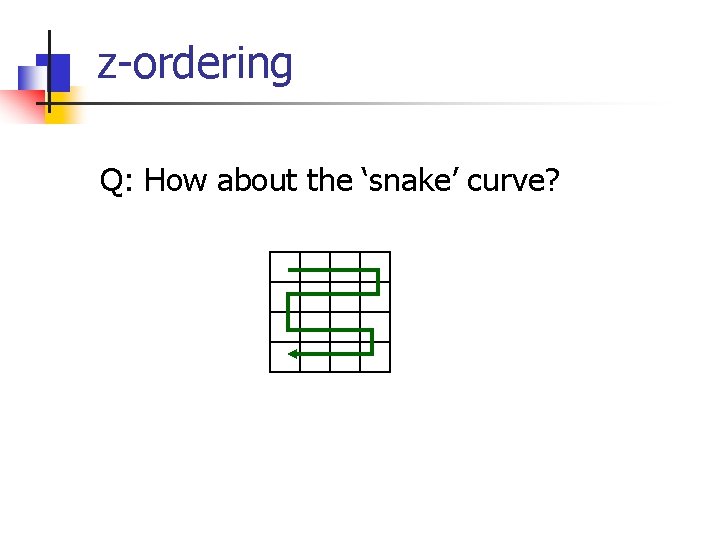
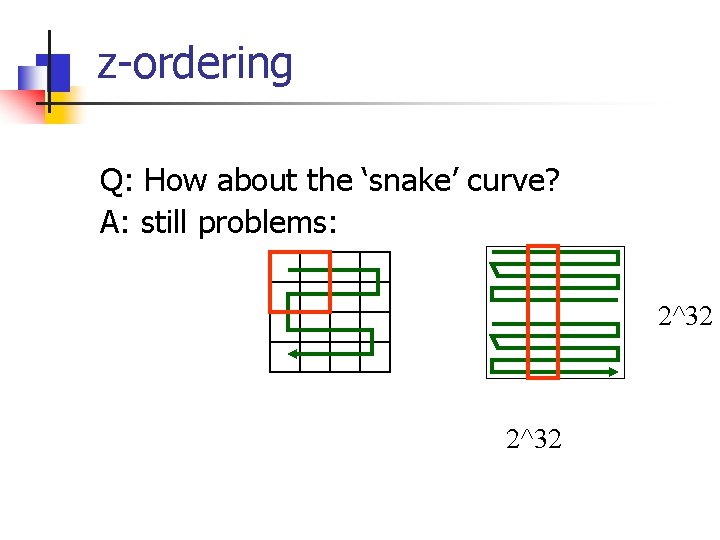
z-ordering Q: How about the ‘snake’ curve?

z-ordering Q: How about the ‘snake’ curve? A: still problems: 2^32

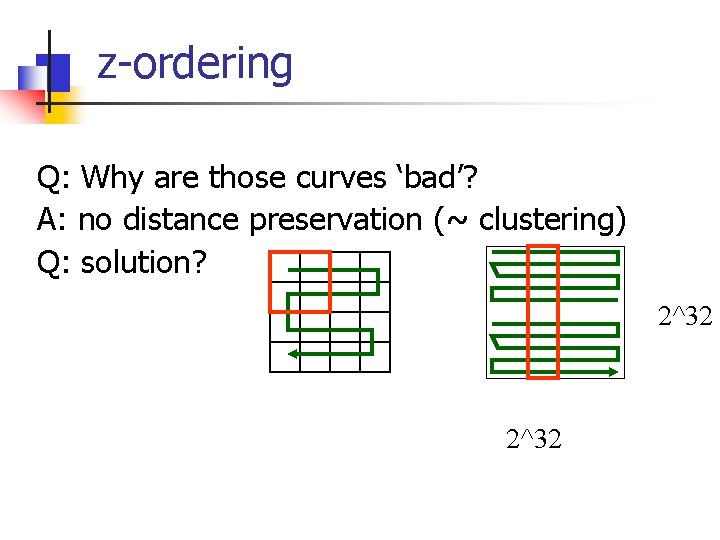
z-ordering Q: Why are those curves ‘bad’? A: no distance preservation (~ clustering) Q: solution? 2^32

z-ordering Q: solution? (w/ good clustering, and easy to compute, for 2 -d and n-d? )

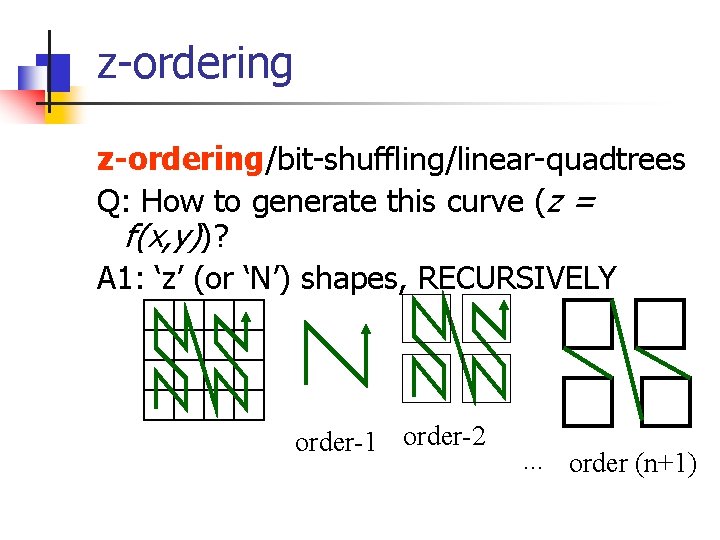
z-ordering Q: solution? (w/ good clustering, and easy to compute, for 2 -d and n-d? ) A: z-ordering/bit-shuffling/linearquadtrees ‘looks’ better: • few long jumps; • scoops out the whole quadrant before leaving it • a. k. a. space filling curves

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y) )? A: 3 (equivalent) answers!

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y))? A 1: ‘z’ (or ‘N’) shapes, RECURSIVELY order-1 order-2 . . . order (n+1)

$z-ordering Notice: n self similar (we’ll see about fractals, soon) n method is hard$

z-ordering Notice: n self similar (we’ll see about fractals, soon) n method is hard to use: z =? f(x, y) order-1 order-2 . . . order (n+1)

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y) )? A: 3 (equivalent) answers! Method #2?

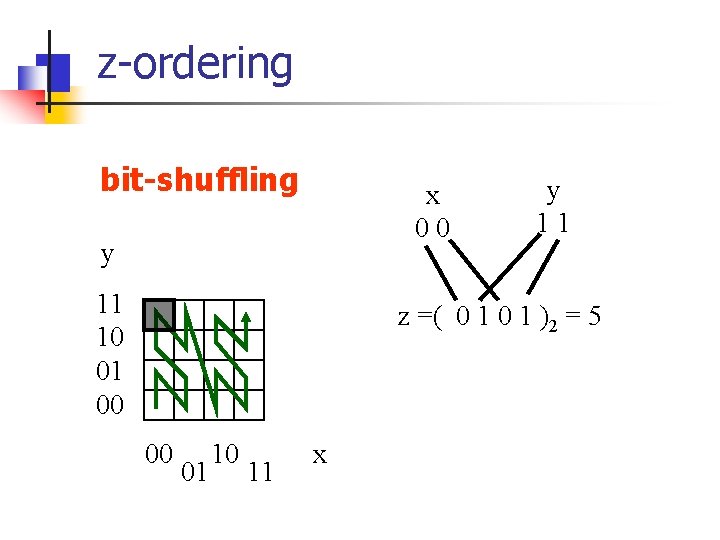
z-ordering bit-shuffling x 00 y 11 10 01 00 y 11 z =( 0 1 )2 = 5 00 01 10 11 x

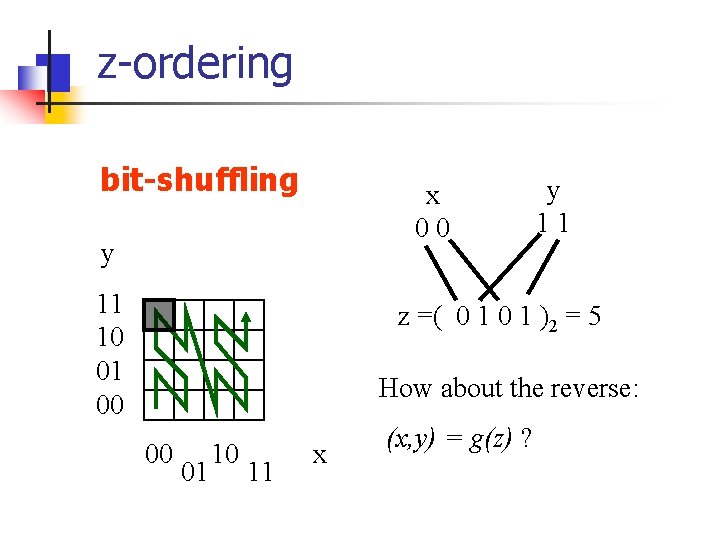
z-ordering bit-shuffling x 00 y 11 10 01 00 y 11 z =( 0 1 )2 = 5 How about the reverse: 00 01 10 11 x (x, y) = g(z) ?

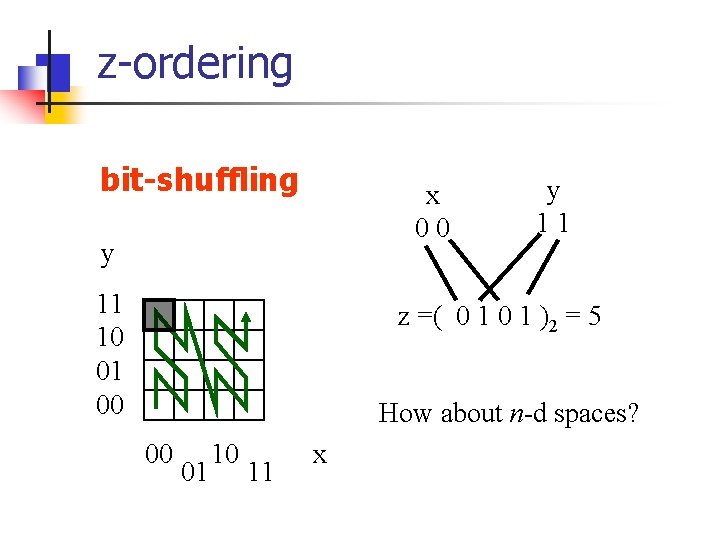
z-ordering bit-shuffling x 00 y 11 10 01 00 y 11 z =( 0 1 )2 = 5 How about n-d spaces? 00 01 10 11 x

z-ordering/bit-shuffling/linear-quadtrees Q: How to generate this curve (z = f(x, y) )? A: 3 (equivalent) answers! Method #3?

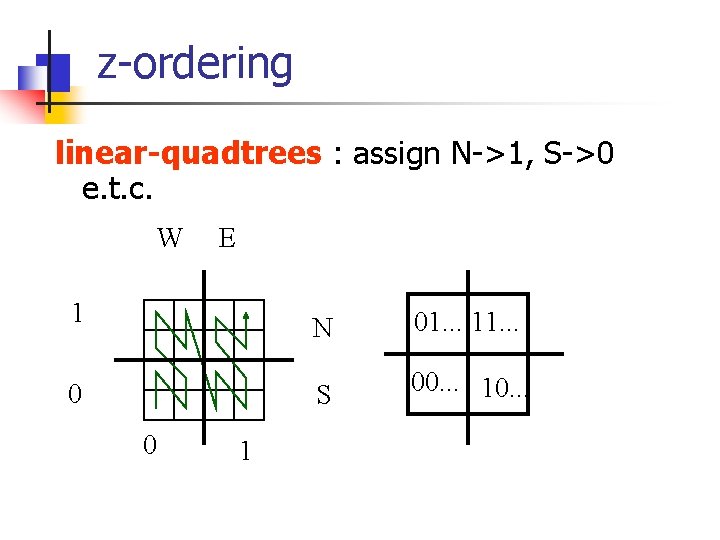
z-ordering linear-quadtrees : assign N->1, S->0 e. t. c. W E 1 0 0 1 N 01. . . 11. . . S 00. . . 10. . .

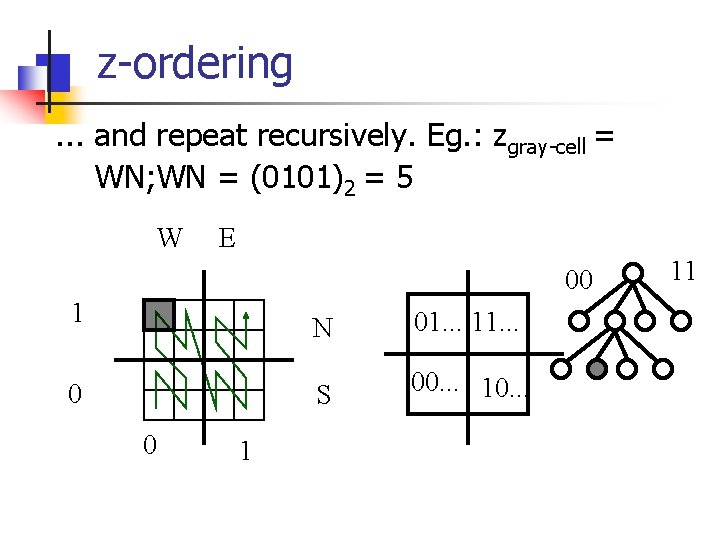
z-ordering. . . and repeat recursively. Eg. : zgray-cell = WN; WN = (0101)2 = 5 W E 00 1 0 0 1 N 01. . . 11. . . S 00. . . 10. . . 11

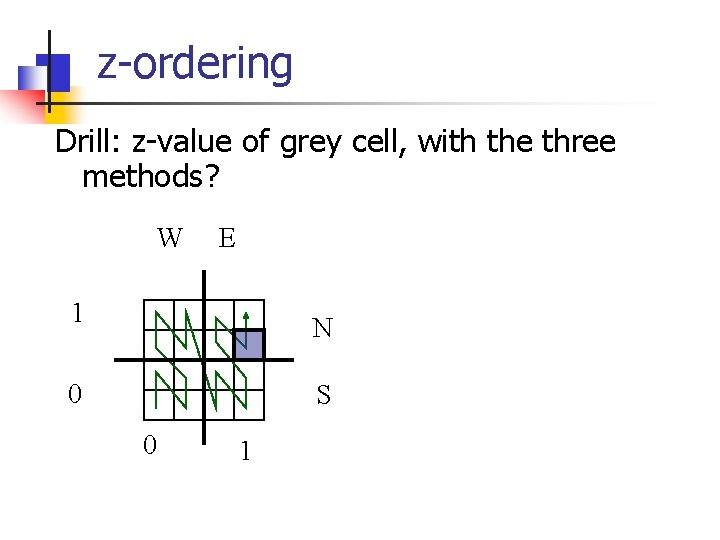
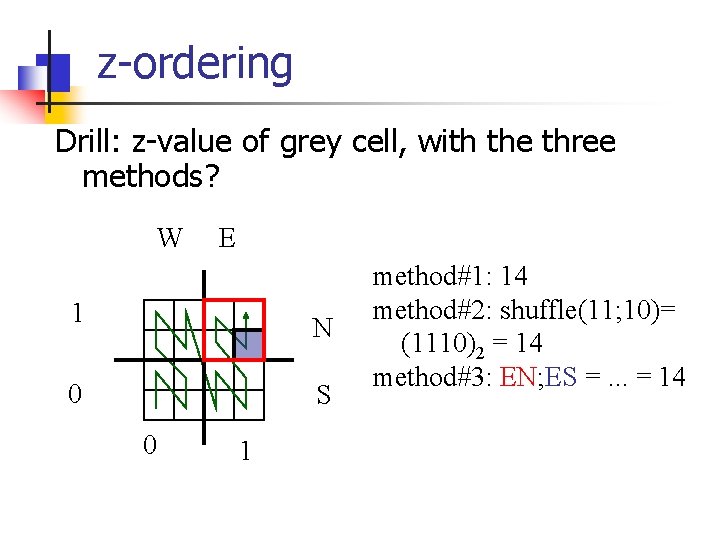
z-ordering Drill: z-value of grey cell, with the three methods? W E 1 N 0 S 0 1

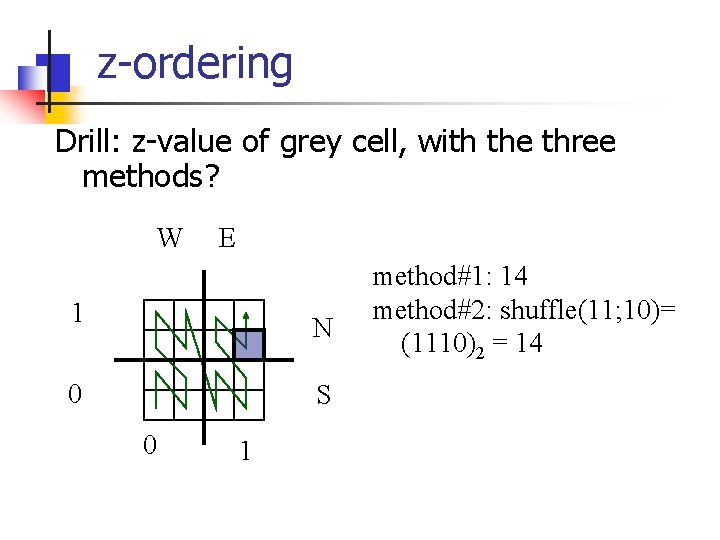
z-ordering Drill: z-value of grey cell, with the three methods? W E 1 N 0 S 0 1 method#1: 14 method#2: shuffle(11; 10)= (1110)2 = 14

z-ordering Drill: z-value of grey cell, with the three methods? W E 1 N 0 S 0 1 method#1: 14 method#2: shuffle(11; 10)= (1110)2 = 14 method#3: EN; ES =. . . = 14

z-ordering - Detailed outline n spatial access methods n z-ordering n n n main idea - 3 methods use w/ B-trees; algorithms (range, knn queries. . . ) non-point (eg. , region) data analysis; variations R-trees

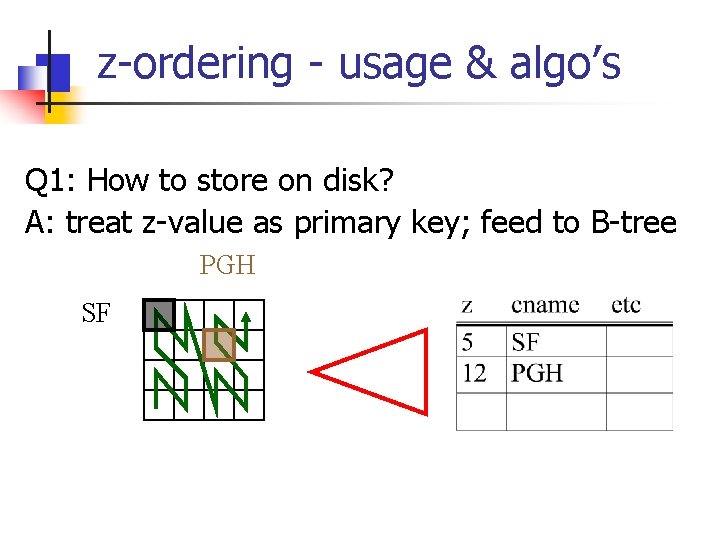
z-ordering - usage & algo’s Q 1: How to store on disk? A: Q 2: How to answer range queries etc

z-ordering - usage & algo’s Q 1: How to store on disk? A: treat z-value as primary key; feed to B-tree PGH SF

z-ordering - usage & algo’s MAJOR ADVANTAGES w/ B-tree: n already inside commercial systems (no coding /debugging!) n concurrency & recovery is ready PGH SF

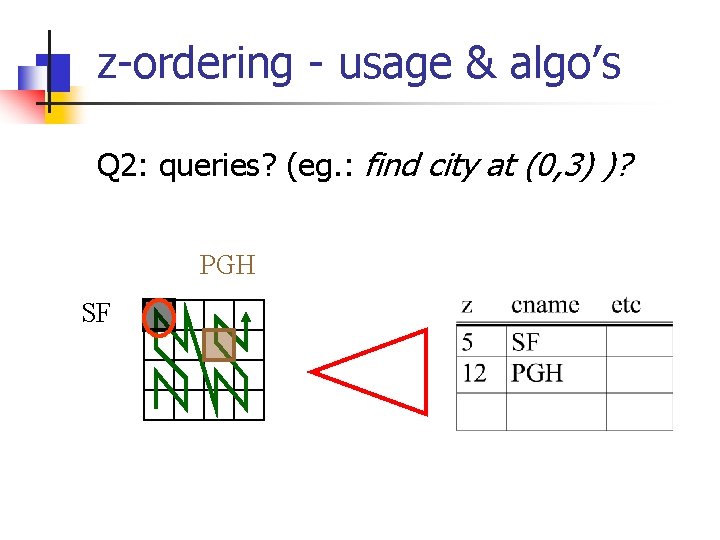
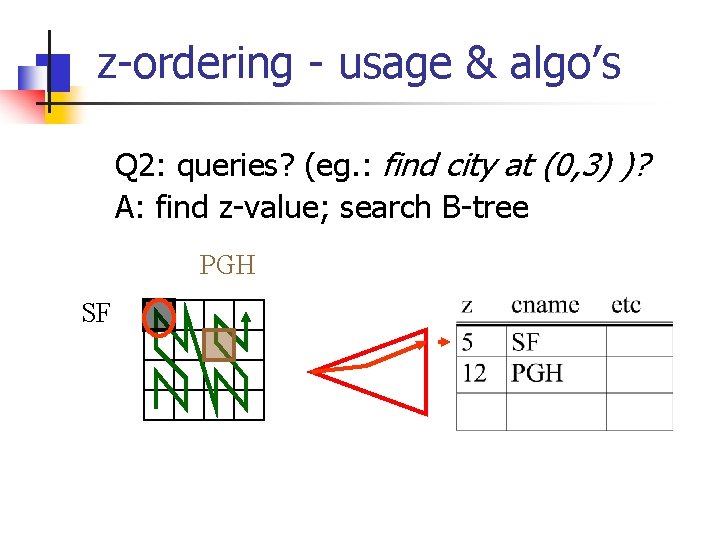
z-ordering - usage & algo’s Q 2: queries? (eg. : find city at (0, 3) )? PGH SF

z-ordering - usage & algo’s Q 2: queries? (eg. : find city at (0, 3) )? A: find z-value; search B-tree PGH SF

z-ordering - usage & algo’s Q 2: range queries? PGH SF

z-ordering - usage & algo’s Q 2: range queries? A: compute ranges of z-values; use B-tree PGH SF 9, 11 -15

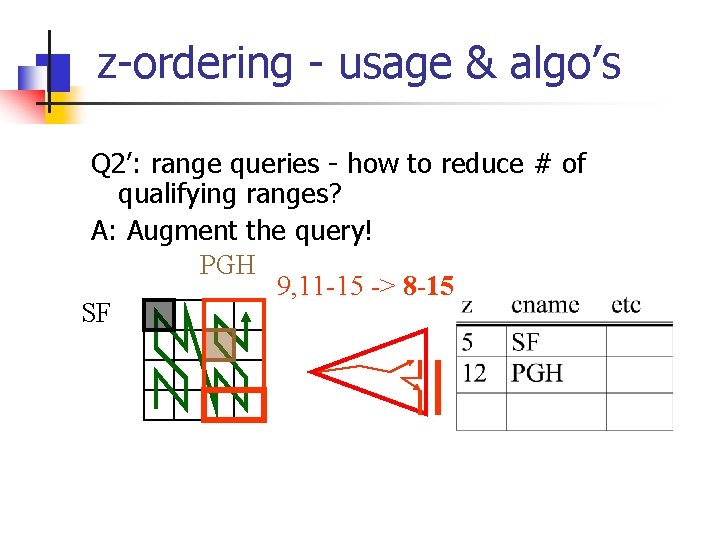
z-ordering - usage & algo’s Q 2’: range queries - how to reduce # of qualifying ranges? PGH SF 9, 11 -15

z-ordering - usage & algo’s Q 2’: range queries - how to reduce # of qualifying ranges? A: Augment the query! PGH 9, 11 -15 -> 8 -15 SF

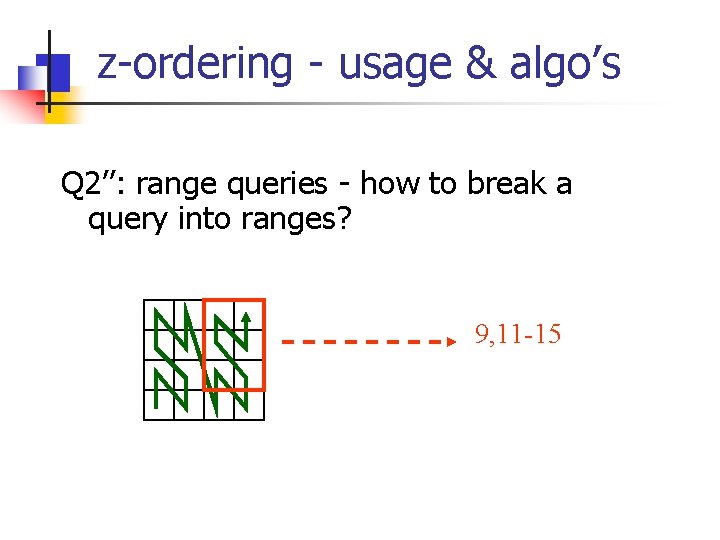
z-ordering - usage & algo’s Q 2’’: range queries - how to break a query into ranges? 9, 11 -15

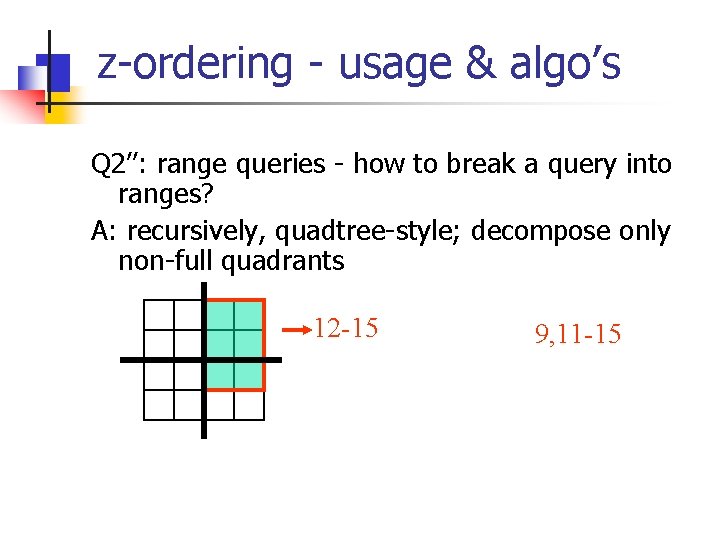
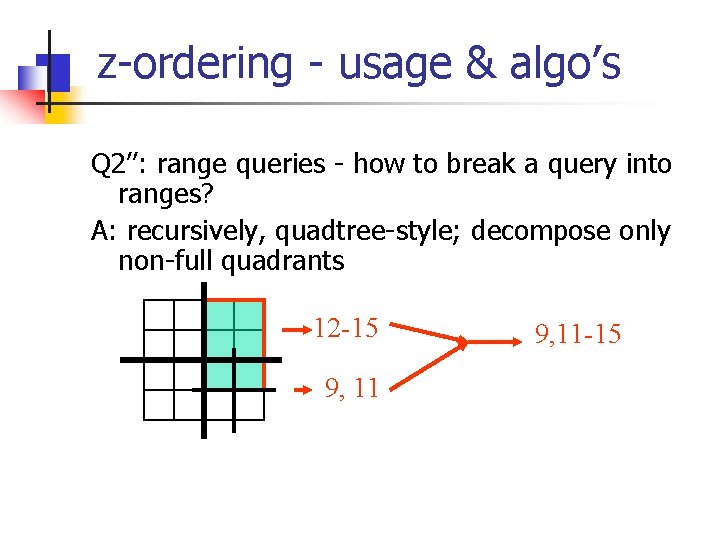
z-ordering - usage & algo’s Q 2’’: range queries - how to break a query into ranges? A: recursively, quadtree-style; decompose only non-full quadrants 12 -15 9, 11 -15

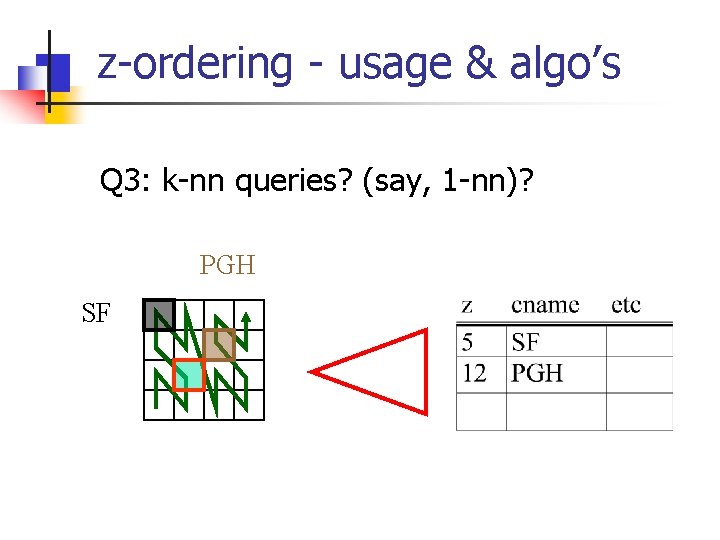
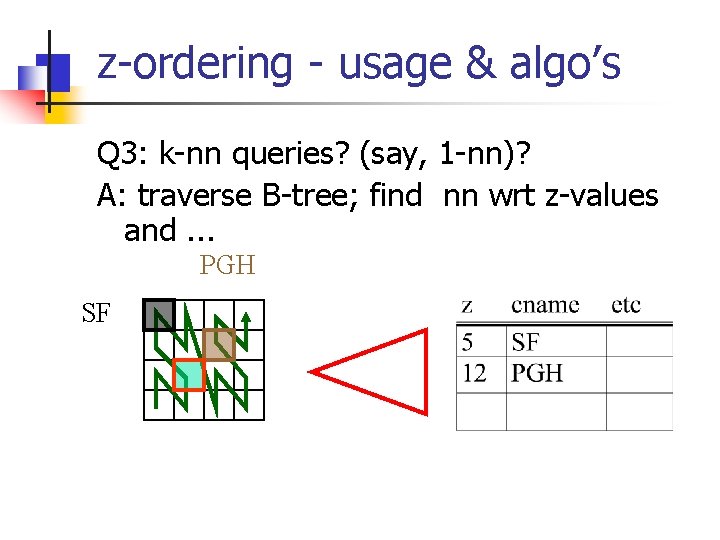
z-ordering - usage & algo’s Q 3: k-nn queries? (say, 1 -nn)? PGH SF

z-ordering - usage & algo’s Q 3: k-nn queries? (say, 1 -nn)? A: traverse B-tree; find nn wrt z-values and. . . PGH SF

z-ordering - usage & algo’s. . . ask a range query. PGH SF nn wrt z-value 3 5 12

z-ordering - usage & algo’s Q 4: all-pairs queries? ( all pairs of cities within 10 miles from each other? ) PGH SF (we’ll see ‘spatial joins’ later: find all PA counties that intersect a lake)

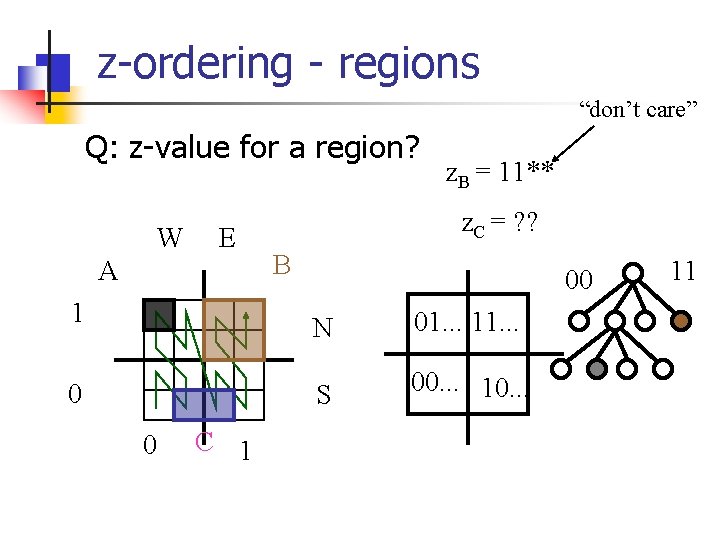
z-ordering - regions Q: z-value for a region? B A C z. B = ? ? z. C = ? ?

z-ordering - regions Q: z-value for a region? A: 1 or more z-values; by quadtree decomposition B A z. B = ? ? z. C = ? ? C

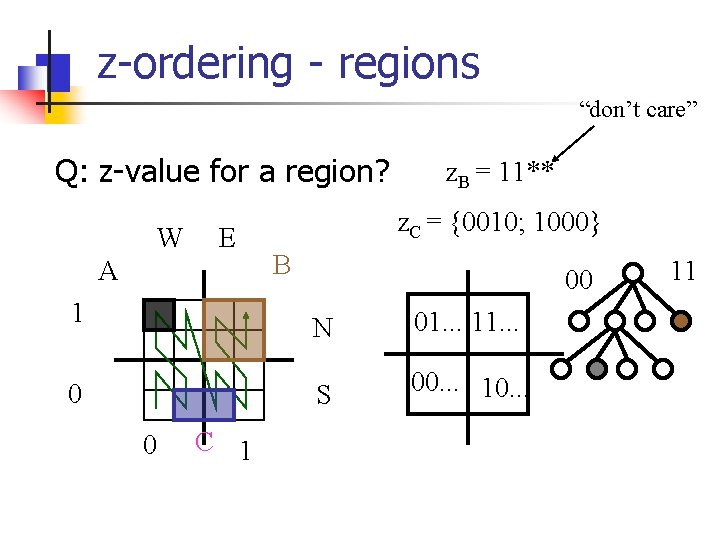
z-ordering - regions “don’t care” Q: z-value for a region? W E A 1 0 0 C 1 z. B = 11** z. C = ? ? B 00 N 01. . . 11. . . S 00. . . 10. . . 11

z-ordering - regions “don’t care” Q: z-value for a region? W E A 1 0 0 C 1 z. B = 11** z. C = {0010; 1000} B 00 N 01. . . 11. . . S 00. . . 10. . . 11

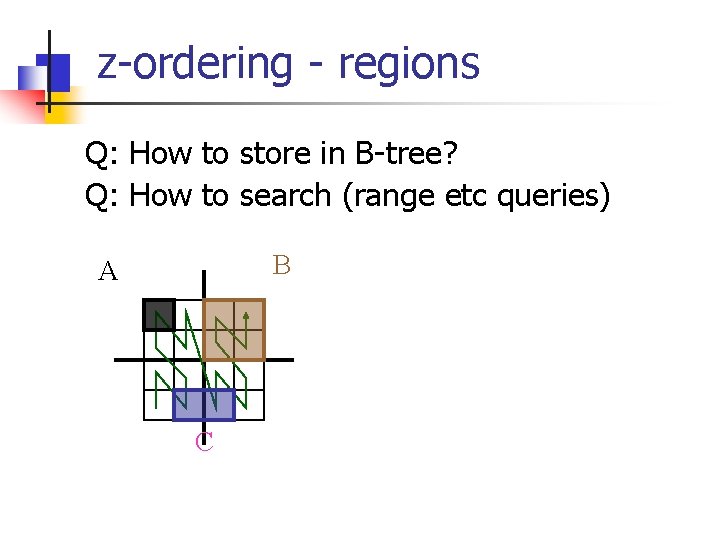
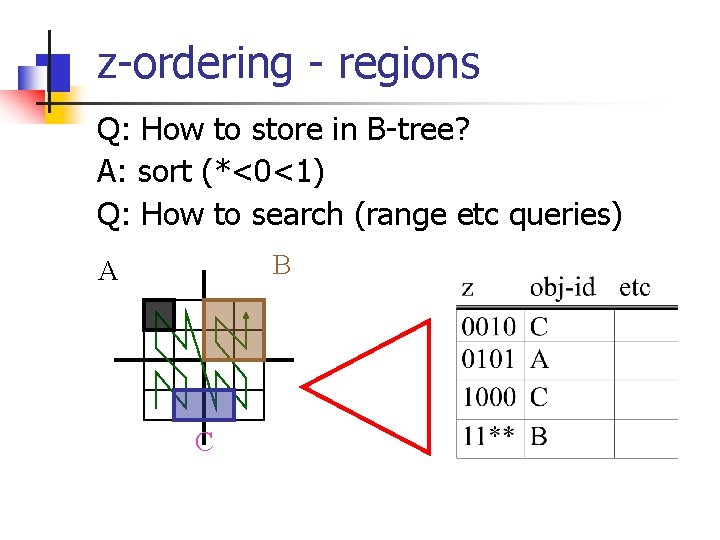
z-ordering - regions Q: How to store in B-tree? Q: How to search (range etc queries) B A C

z-ordering - regions Q: How to store in B-tree? A: sort (*<0<1) Q: How to search (range etc queries) B A C

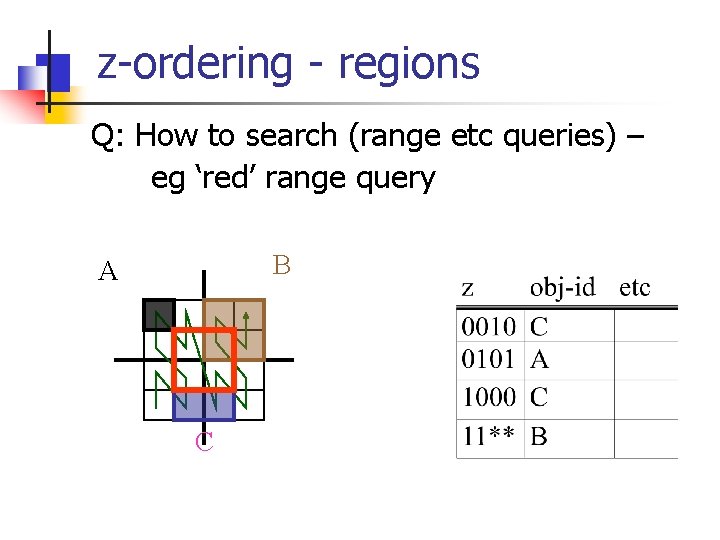
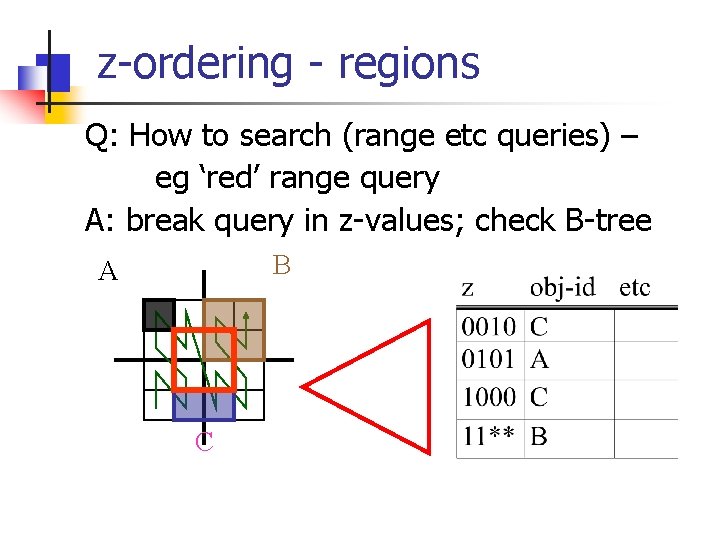
z-ordering - regions Q: How to search (range etc queries) – eg ‘red’ range query B A C

z-ordering - regions Q: How to search (range etc queries) – eg ‘red’ range query A: break query in z-values; check B-tree B A C

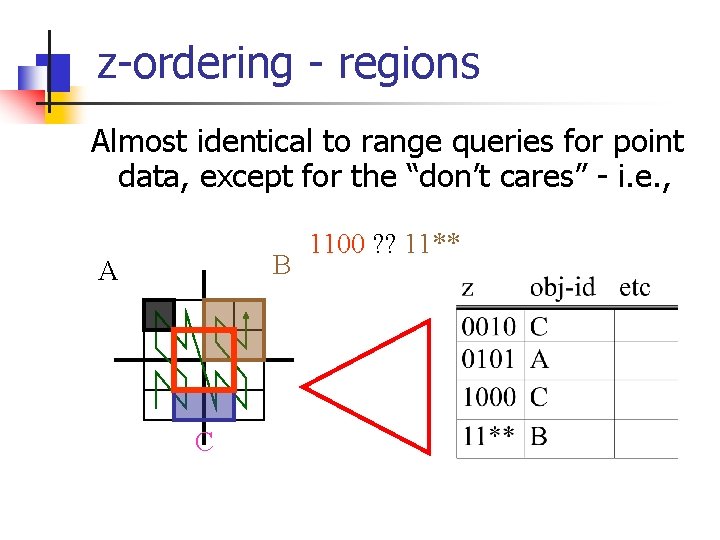
z-ordering - regions Almost identical to range queries for point data, except for the “don’t cares” - i. e. , B A C 1100 ? ? 11**

z-ordering - regions Almost identical to range queries for point data, except for the “don’t cares” - i. e. , z 1= 1100 ? ? 11** = z 2 Specifically: does z 1 contain/avoid/intersect z 2? Q: what is the criterion to decide?

z-ordering - regions z 1= 1100 ? ? 11** = z 2 Specifically: does z 1 contain/avoid/intersect z 2? Q: what is the criterion to decide? A: Prefix property: let r 1, r 2 be the corresponding regions, and let r 1 be the smallest (=> z 1 has fewest ‘*’s). Then:

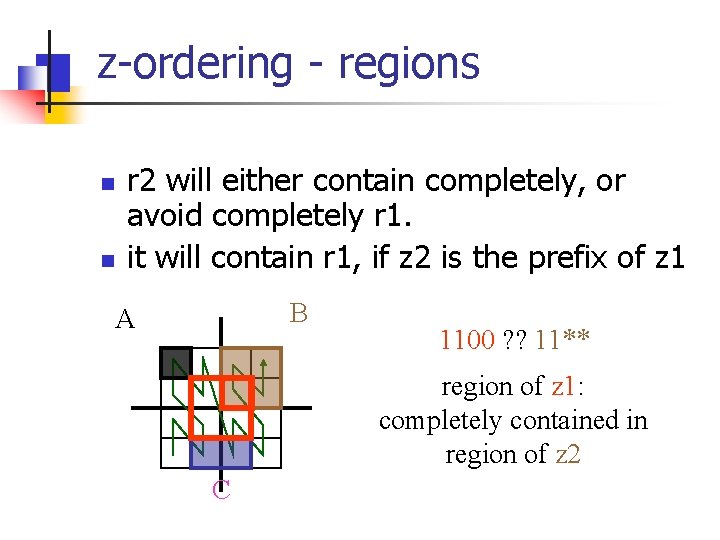
z-ordering - regions n n r 2 will either contain completely, or avoid completely r 1. it will contain r 1, if z 2 is the prefix of z 1 B A 1100 ? ? 11** region of z 1: completely contained in region of z 2 C

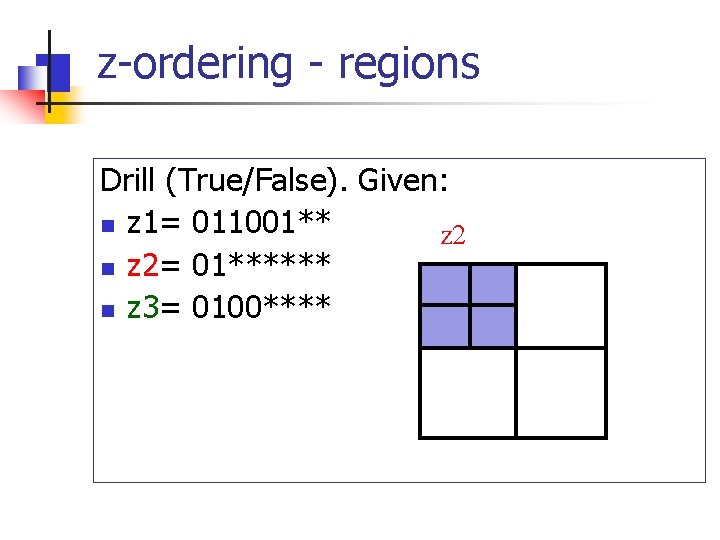
z-ordering - regions Drill (True/False). Given: n z 1= 011001** n z 2= 01****** n z 3= 0100**** T/F r 2 contains r 1 T/F r 3 contains r 2

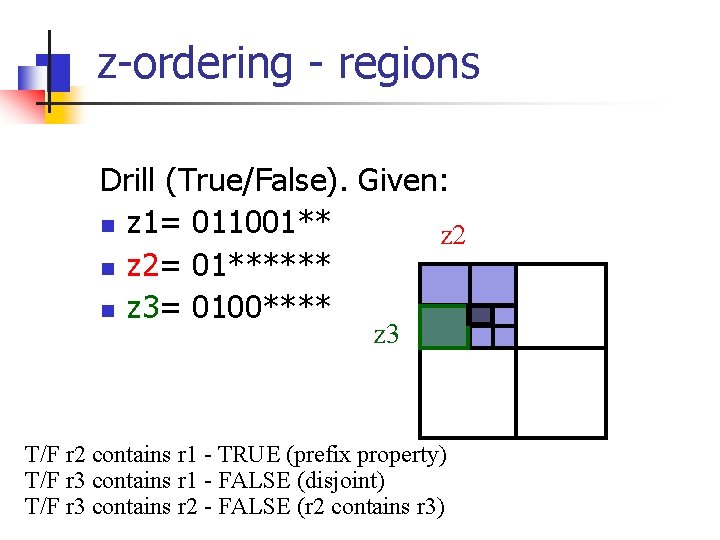
z-ordering - regions Drill (True/False). Given: n z 1= 011001** n z 2= 01****** n z 3= 0100**** T/F r 2 contains r 1 - TRUE (prefix property) T/F r 3 contains r 1 - FALSE (disjoint) T/F r 3 contains r 2 - FALSE (r 2 contains r 3)

z-ordering - regions Drill (True/False). Given: n z 1= 011001** z 2 n z 2= 01****** n z 3= 0100****

z-ordering - regions Drill (True/False). Given: n z 1= 011001** z 2 n z 2= 01****** n z 3= 0100**** z 3 T/F r 2 contains r 1 - TRUE (prefix property) T/F r 3 contains r 1 - FALSE (disjoint) T/F r 3 contains r 2 - FALSE (r 2 contains r 3)

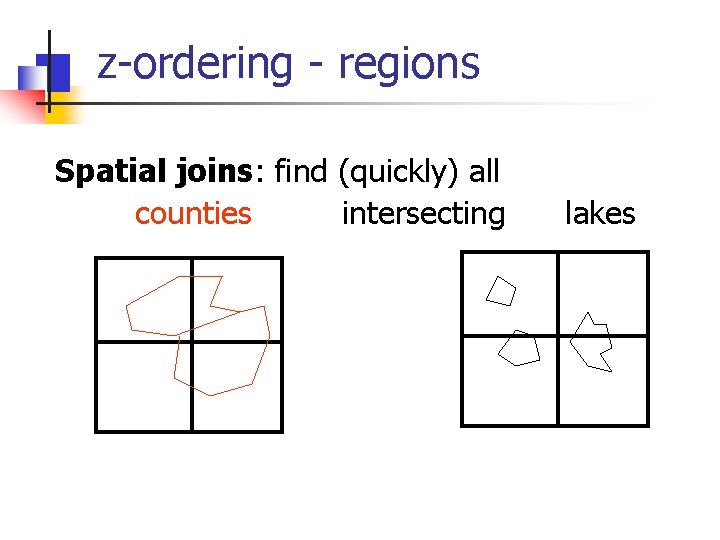
z-ordering - regions Spatial joins: find (quickly) all counties intersecting lakes

z-ordering - regions Spatial joins: find (quickly) all counties intersecting Naive algorithm: O( N * M) Something faster? lakes

z-ordering - regions Spatial joins: find (quickly) all counties intersecting lakes

z-ordering - regions Spatial joins: find (quickly) all counties intersecting lakes Solution: merge the lists of (sorted) z-values, looking for the prefix property footnote#1: ‘*’ needs careful treatment footnote#2: need dup. elimination

z-ordering - variations Q: is z-ordering the best we can do?

z-ordering - variations Q: is z-ordering the best we can do? A: probably not - occasional long ‘jumps’ Q: then?

z-ordering - variations Q: is z-ordering the best we can do? A: probably not - occasional long ‘jumps’ Q: then? A 1: Gray codes

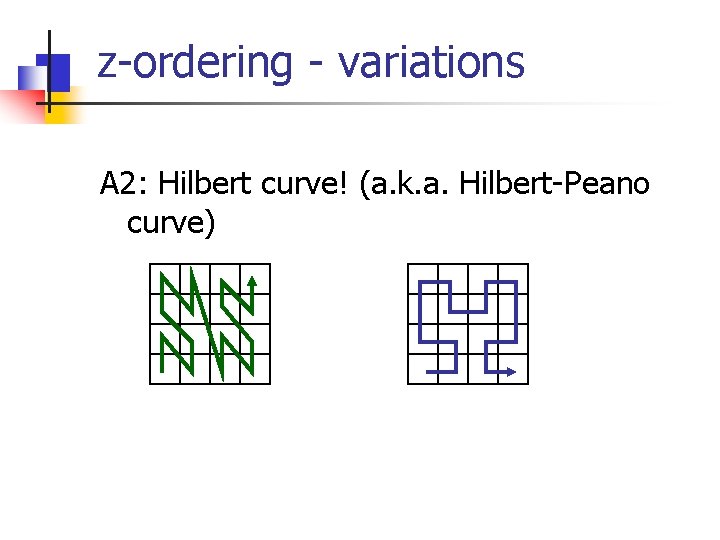
z-ordering - variations A 2: Hilbert curve! (a. k. a. Hilbert-Peano curve)

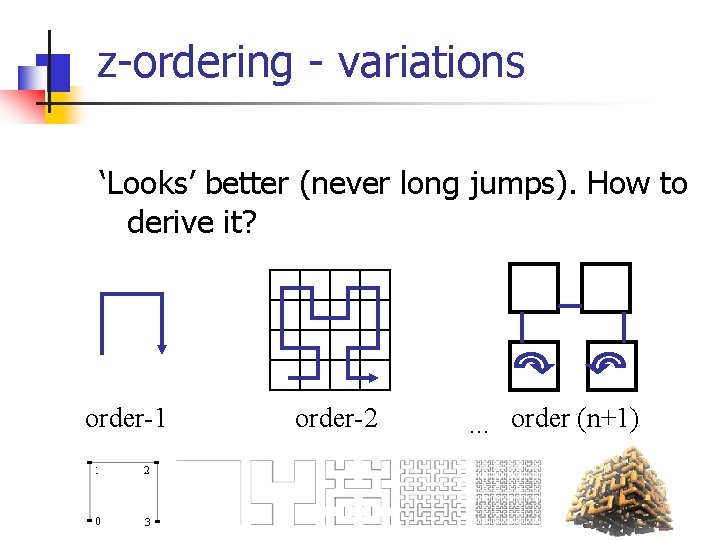
z-ordering - variations ‘Looks’ better (never long jumps). How to derive it?

z-ordering - variations ‘Looks’ better (never long jumps). How to derive it? order-1 order-2 . . . order (n+1)

z-ordering - variations Q: function for the Hilbert curve ( h = f(x, y) )? A: bit-shuffling, followed by post-processing, to account for rotations. Linear on # bits. See textbook, for pointers to code/algorithms (eg. , [Jagadish, 90])

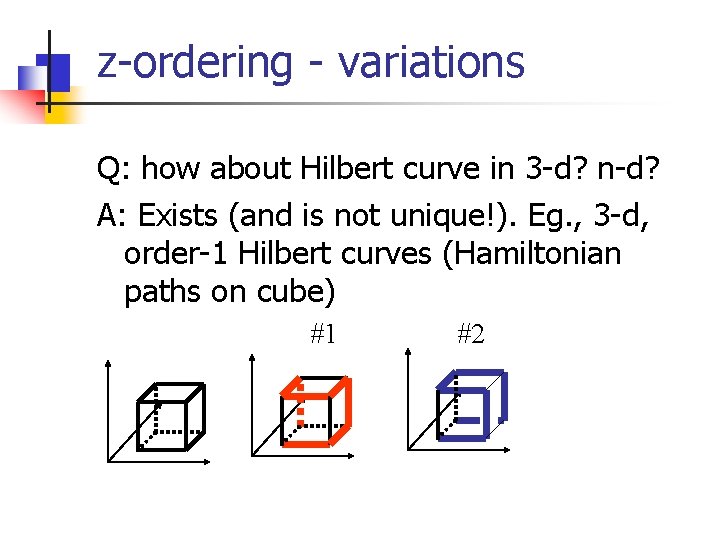
z-ordering - variations Q: how about Hilbert curve in 3 -d? n-d? A: Exists (and is not unique!). Eg. , 3 -d, order-1 Hilbert curves (Hamiltonian paths on cube) #1 #2

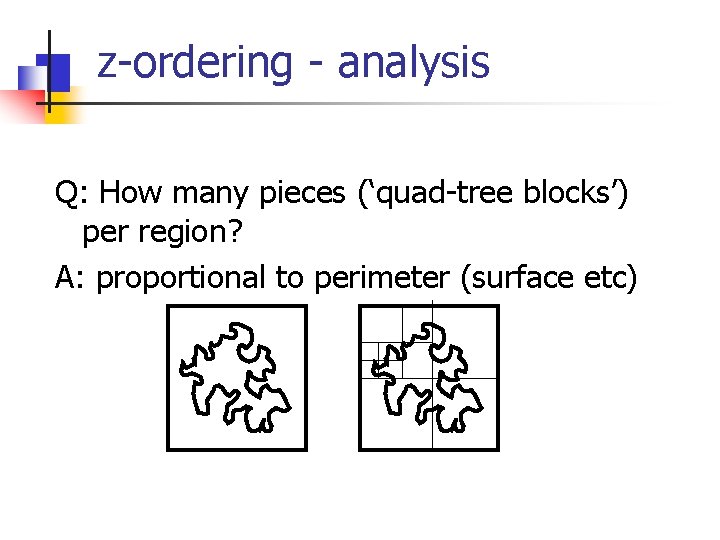
z-ordering - analysis Q: How many pieces (‘quad-tree blocks’) per region? A: proportional to perimeter (surface etc)

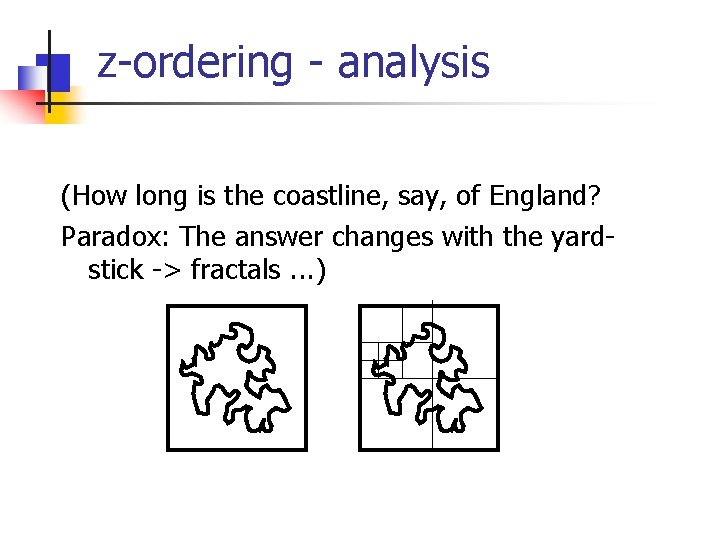
z-ordering - analysis (How long is the coastline, say, of England? Paradox: The answer changes with the yardstick -> fractals. . . )

z-ordering - analysis Q: Should we decompose a region to full detail (and store in B-tree)?

z-ordering - analysis Q: Should we decompose a region to full detail (and store in B-tree)? A: NO! approximation with 1 -3 pieces/zvalues is best [Orenstein 90]

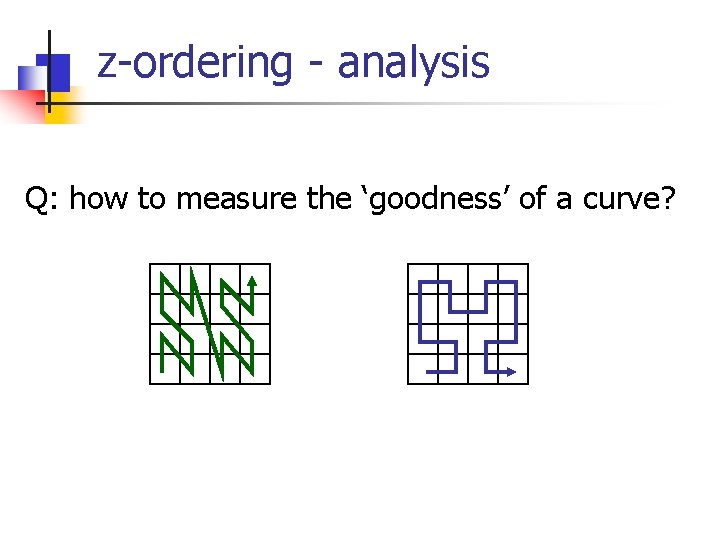
z-ordering - analysis Q: how to measure the ‘goodness’ of a curve?

z-ordering - analysis Q: how to measure the ‘goodness’ of a curve? A: e. g. , avg. # of runs, for range queries 4 runs 3 runs (#runs ~ #disk accesses on B-tree)

z-ordering - analysis Q: So, is Hilbert really better? A: 27% fewer runs, for 2 -d (similar for 3 -d) Q: are there formulas for #runs, #of quadtree blocks etc? A: Yes ([Jagadish; Moon+ etc] see textbook)

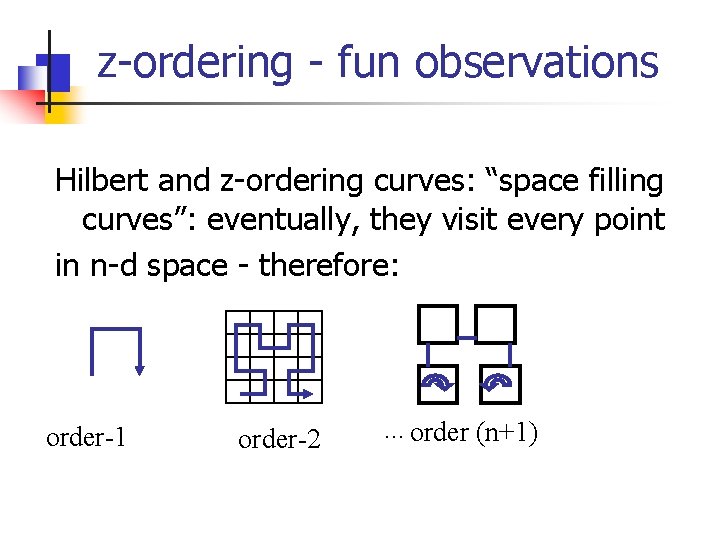
z-ordering - fun observations Hilbert and z-ordering curves: “space filling curves”: eventually, they visit every point in n-d space - therefore: order-1 order-2 . . . order (n+1)

z-ordering - fun observations. . . they show that the plane has as many points as a line (-> headaches for 1900’s mathematics/topology). (fractals, again!) order-1 order-2 . . . order (n+1)

z-ordering - fun observations Observation #2: Hilbert (like) curve for video encoding [Y. Matias+, CRYPTO ‘ 87]: Given a frame, visit its pixels in randomized hilbert order; compress; and transmit

z-ordering - fun observations In general, Hilbert curve is great for preserving distances, clustering, vector quantization etc

Conclusions n n n z-ordering is a great idea (n-d points -> 1 -d points; feed to B-trees) used by TIGER system and (most probably) by other GIS products works great with low-dim points