CIS 540 Principles of Embedded Computation Spring 2016

CIS 540 Principles of Embedded Computation Spring 2016 http: //www. seas. upenn. edu/~cis 540/ Instructor: Rajeev Alur alur@cis. upenn. edu

Recap: Symbolic Transition Systems q Region over variables X is a data structure that represents a set of states assigning values to X q Transition system T with state variables S represented by § Region j. I over S for initial states § Region j. T over S U S’ for transitions q Symbolic representation can be compiled automatically from code for updating variables § To get j. T from reaction description of a Synchronous Reactive Component, local/input/output vars must be existentially quantified (see textbook for examples) CIS 540 Spring 2016; Lecture Feb 15

Operations on Regions q In general, we want to represent sets of states by a data type reg, which should support following operations q Disj(A, B): Returns region that contains states either in A or in B § For formulas, this is just “A | B” q Conj(A, B): Returns region containing states that are in both A and B § For formulas, this is just “A & B” q Diff(A, B): Returns region containing states in A but not in B § For formulas, this is “A & ~B” q Is. Empty(A): Returns 0 if region A contains some state, and 1 otherwise § For formulas, this requires testing “satisfiability”: can the variables in the formulas assigned values to make formula true q Exists(A, X): Returns projection of A by quantifying variables in X § For formulas, this requires “quantifier elimination” q Rename(A, X, Y): Rename variables in X to corresponding vars in Y § For formulas, this is textual substitution CIS 540 Spring 2016; Lecture Feb 15

Symbolic Image Computation q Given: § A of type reg over state variables S § Trans of type reg over S U S’ q Post(A, Trans) = Rename(Exists(Conj(A, Trans), S’, S) 1. Take conjunction of A and Trans 2. Project out the variables in S using existential quantification 3. Rename primed variables to get a region over S CIS 540 Spring 2016; Lecture Feb 15

Symbolic Breadth-First-Search Algorithm reach 0 = Initial states and each reachi+1 obtained from reachi by applying Post q q Algorithm for checking if a property j is an invariant of T? Same as checking if an “error” state satisfying ~j is reachable? We need to check at every step if error states reached; if so, stop. If no new states are encountered, then also stop (invariant satisfied) CIS 540 Spring 2016; Lecture Feb 15

Symbolic BFS Algorithm Given region Init over S, region Trans over S U S’, and region j over S, if j is reachable in T then return 1, else return 0 reg Reach : = Init; /* States found reachable */ reg New : = Init; /* States not yet explored for outgoing transitions */ while Is. Empty(New) = 0 { /* while there are states to be explored */ if Is. Empty(Conj(New, j)) =0 /* Property j found reachable */ then return 1 (and stop); New : = Diff(Post(New, Trans), Reach); /*These are states in post-image of New, but not previously found reachable, so to be explored */ Reach : = Disj(Reach, New); /* Update Reach by newly found states*/ }; return 0; /* All states explored without encountering j */ CIS 540 Spring 2016; Lecture Feb 15

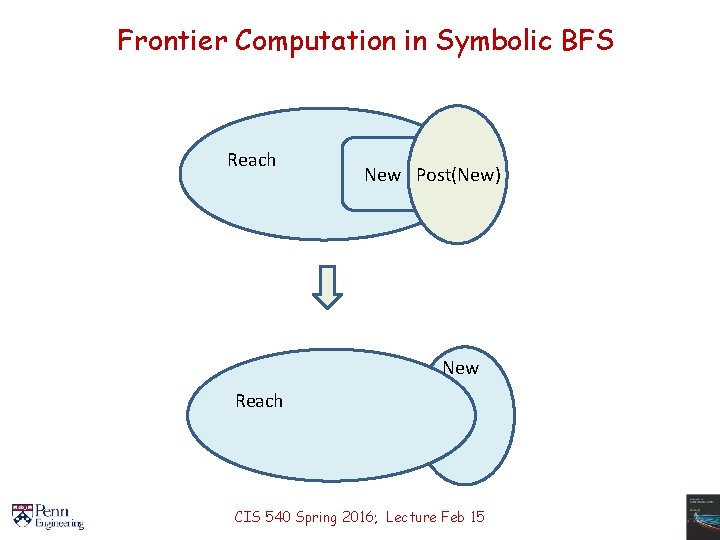
Frontier Computation in Symbolic BFS Reach New Post(New) New Reach CIS 540 Spring 2016; Lecture Feb 15

Symbolic Search q Correctness: When the algorithm stops, its answer (whether the property j is reachable or not) is correct q Termination: Number of iterations depends on § length of shortest execution leading to a state satisfying j § Diameter: smallest d such that all states reachable within d steps (this may not be bounded, if system is not finite-state) § In practice, terminates if one of these numbers is small q Used in practice for hardware verification, protocol verification § Industrial-strength symbolic model checker: Cadence § Open-source widely used academic tool: Nu. SMV CIS 540 Spring 2016; Lecture Feb 15

Implementation of Regions q Key to efficient implementation: How to represent regions? § Operations: Disj, Conj, Diff, Is. Empty, Exists, Rename q Suppose all variables are Booleans q Can we represent regions with formulas (with &, |, ~) § Disj, Conj, Diff, Rename easy § Exists (j, x) same as j [x->0] | j [x->1] § Is. Empty(j) requires test for satisfiability (SAT) q SAT is computationally demanding (NP-complete), but more importantly, size of formula representing Reach keeps growing as we apply operations such as Conj, Disj, Exists… § Key to performance: Simplify formulas as much as possible § Solution: Data structure of ROBDDs CIS 540 Spring 2016; Lecture Feb 15

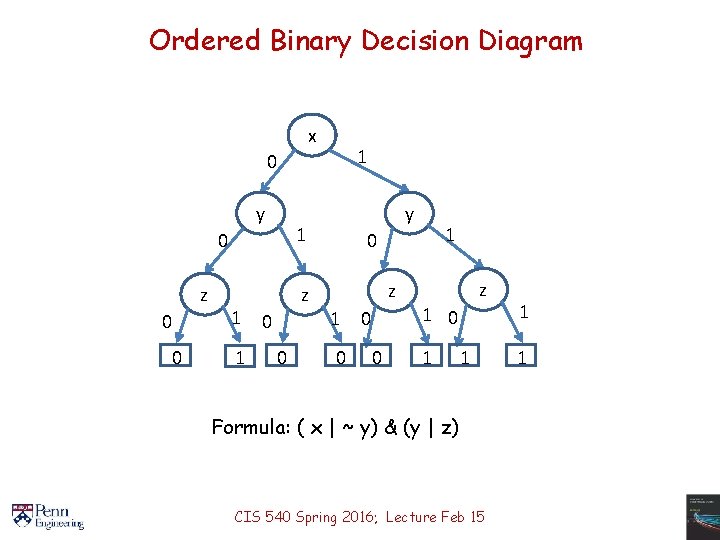
Ordered Binary Decision Diagram x 1 0 y 1 0 z 0 0 1 1 y z 0 0 1 0 z 1 0 0 0 z 1 0 1 1 Formula: ( x | ~ y) & (y | z) CIS 540 Spring 2016; Lecture Feb 15 1 1

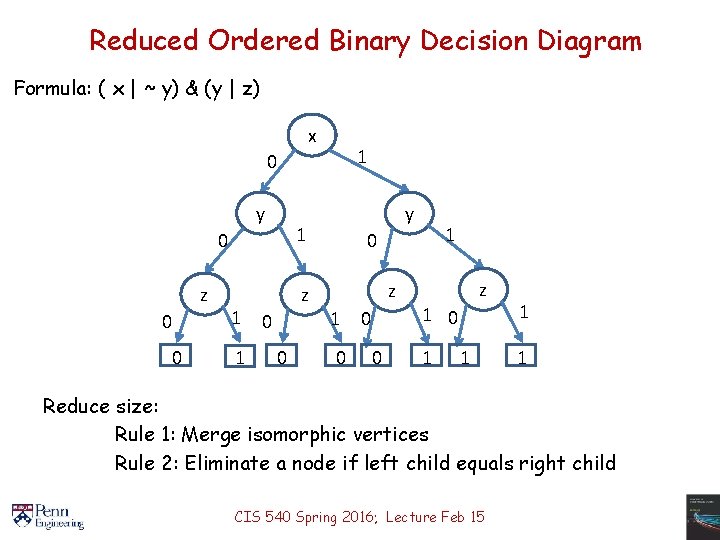
Reduced Ordered Binary Decision Diagram Formula: ( x | ~ y) & (y | z) x 1 0 y 1 0 z 0 0 1 1 y z 0 0 1 0 z 1 0 0 0 z 1 0 1 1 Reduce size: Rule 1: Merge isomorphic vertices Rule 2: Eliminate a node if left child equals right child CIS 540 Spring 2016; Lecture Feb 15

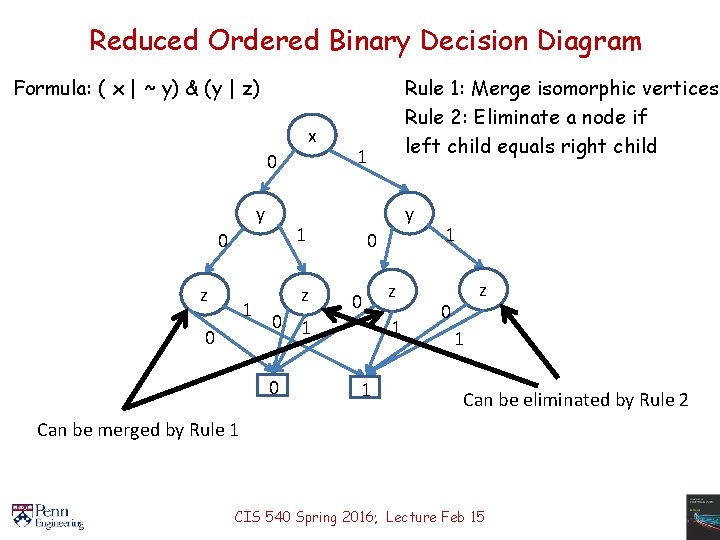
Reduced Ordered Binary Decision Diagram Formula: ( x | ~ y) & (y | z) x 0 y z 1 0 1 y 1 0 z 0 1 0 Rule 1: Merge isomorphic vertices Rule 2: Eliminate a node if left child equals right child 0 0 z 1 1 1 z 0 1 Can be eliminated by Rule 2 Can be merged by Rule 1 CIS 540 Spring 2016; Lecture Feb 15

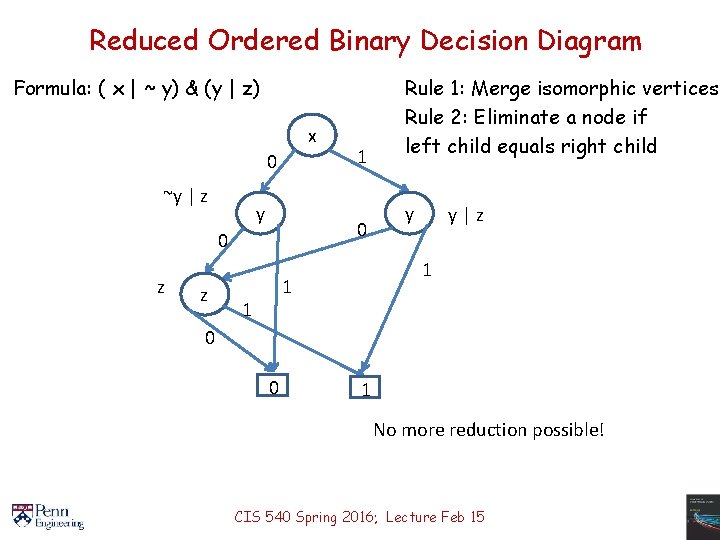
Reduced Ordered Binary Decision Diagram Formula: ( x | ~ y) & (y | z) x 0 ~y | z y 0 0 z z 1 y y|z 1 1 1 Rule 1: Merge isomorphic vertices Rule 2: Eliminate a node if left child equals right child 0 0 1 No more reduction possible! CIS 540 Spring 2016; Lecture Feb 15

ROBDD Properties q Key restriction: Variables appear in same order on each path § Not every variable needs to appear on every path q The order in which reductions are applied does not matter § Final result depends only on the function being represented § Once we fix variable ordering, corresponding ROBDD is canonical q Minimal: Smallest possible decision graph given the ordering restriction § No other reductions possible q One does not have to first build the complete tree, and then reduce CIS 540 Spring 2016; Lecture Feb 15

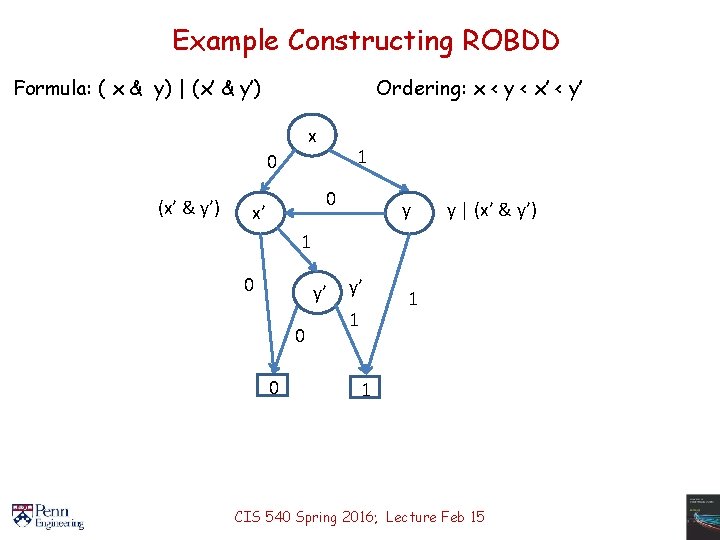
Example Constructing ROBDD Formula: ( x & y) | (x’ & y’) Ordering: x < y < x’ < y’ x 1 0 (x’ & y’) 0 x’ y y | (x’ & y’) 1 0 y’ 0 0 y’ 1 1 1 CIS 540 Spring 2016; Lecture Feb 15

ROBDD Definition Given a set X of Boolean vars ordered by <, ROBDD B consists of q Finite set U of vertices partitioned into internal and terminal q Labeling function: for internal vertex u, label(u) is a variable in X and for terminal vertex u, label(u) is a constant 0/1 q Left-child function for internal vertices such that either left(u) is terminal, or label(u) < label(left(u)) q Right-child function for internal vertices such that either right(u) is terminal, or label(u) < label(right(u)) q Meets the reduction rules: 1. If u and v are distinct terminal vertices then label(u) != label(v) 2. If u and v are distinct internal vertices then either label(u) != label(v) or left(u) != left(v) or right(u) != right(v) 3. If u is internal vertex, then left(u) != right(u) q Semantics of a vertex: Boolean function associated with it CIS 540 Spring 2016; Lecture Feb 15

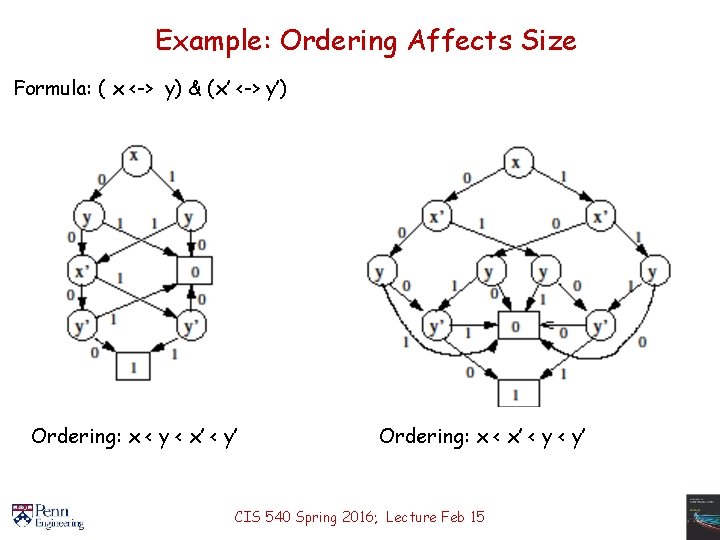
Example: Ordering Affects Size Formula: ( x <-> y) & (x’ <-> y’) Ordering: x < y < x’ < y’ Ordering: x < x’ < y’ CIS 540 Spring 2016; Lecture Feb 15

ROBDD Properties q For every Boolean function/formula f over variables V, given an ordering <, there exists a unique ROBDD for f over (V, <) q To test if two formulas/circuits f and g are equivalent, we can build ROBDDs for f and g, check if they are the same q Satisfiability/emptiness test: Given an ROBDD B, is the corresponding function satisfiable? § B is satisfiable if it does not equal terminal vertex 0 q Validity test: Given an ROBDD B, is the corresponding function valid (that is, always 1 no matter what the values of variables are) § B is valid if it equals terminal vertex 1 q How to reconcile this with the computational difficulty of checking satisfiability/validity of formulas/circuits? § ROBDD corresponding to a formula can be exponentially large! § For some functions, no matter what ordering we choose, the ROBDD is guaranteed to be large! (Hope: this is not a common case) CIS 540 Spring 2016; Lecture Feb 15

ROBDD Implementation q Efficient data structures and implementations known q Algorithms for operations such as Conj, Disj, Diff § Given ROBDDs B 1 and B 2, construct ROBDD representing the AND of corresponding functions directly q Given a formula/circuit/program-text construct ROBDD representing the corresponding transition relation q How to choose a “good” variable ordering? q See textbook (page 115 onwards) for some basic ideas for efficient implementation CIS 540 Spring 2016; Lecture Feb 15