CIS 4526 Foundations of Machine Learning Linear Classification

CIS 4526: Foundations of Machine Learning Linear Classification : Perceptron (modified from Yaser Abu-Mostafa and Mohamed Batouche) Instructor: Kai Zhang CIS @ Temple University, Fall 2020

Creditworthiness • Banks would like to decide whether or not to extend credit to new customers – Good customers pay back loans – Bad customers default • Problem: Predict creditworthiness based on: – Salary, Years in residence, Current debt, Age, etc. 2

Digit Classification 3

Classification Problem • Key Concepts – Binary or multi-classification – Classification as regression – Decision boundary – A simple Algorithm: Perceptron 4

Classification vs Regression 5

Classification as Regression 6

Classification as Regression 7

Classification as Regression The regression function (the line) does not fit the actual target (1, -1) very well (the loss function is not very suitable) Nevertheless, we can still use the notso-perfect regression function to achieve classification task, by defining the decision rule 8

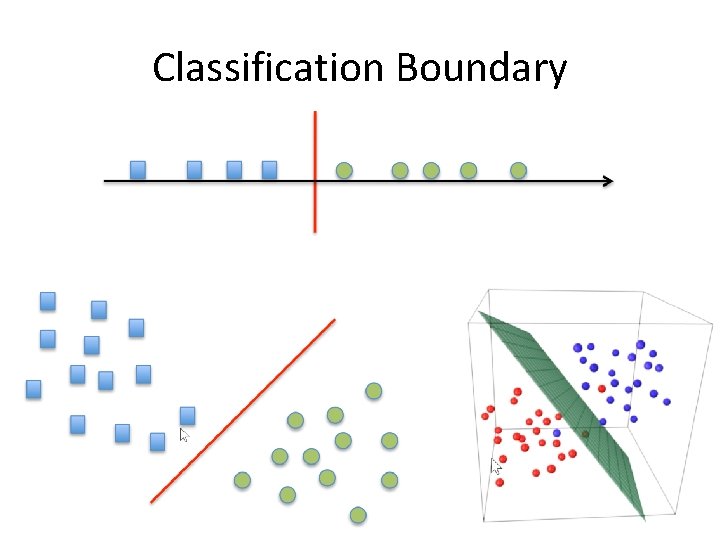
Classification Boundary 9

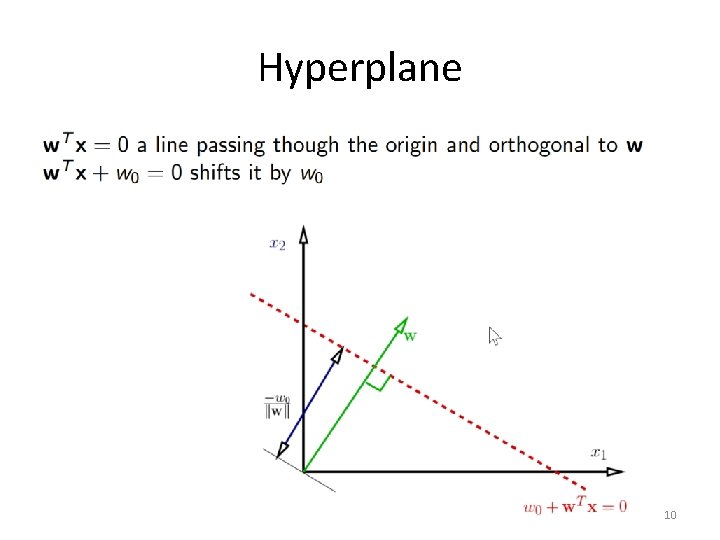
Hyperplane 10

Can we have a better loss function for Classification? 11

A Loss Function for Classification 12

Perceptron Algorithm for linear classification • Minimizing the loss of classification (we have just defined) is not that easy! • We will first introduce a super-easy heuristic procedure to solve linear classification: Perceptron • In the future, we will prove that Perceptron is indeed minimizing the loss of classification we defined. 13

Perceptron • For a customer, – Approve credit if – Deny credit if • This linear formula can be written as: 14

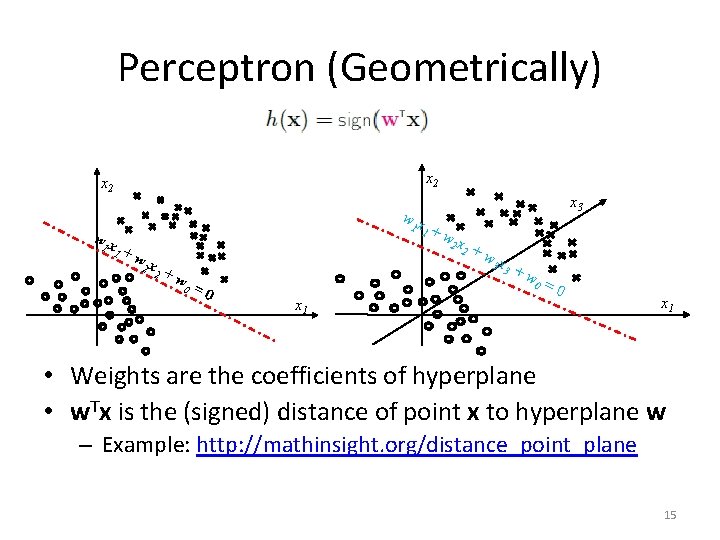
Perceptron (Geometrically) x 2 wx 1 1 wx 1 +w 2 x 2 +w 0 =0 1 x 3 +w 2 x 2 +w 3 x 3 +w 0 x 1 =0 x 1 • Weights are the coefficients of hyperplane • w. Tx is the (signed) distance of point x to hyperplane w – Example: http: //mathinsight. org/distance_point_plane 15

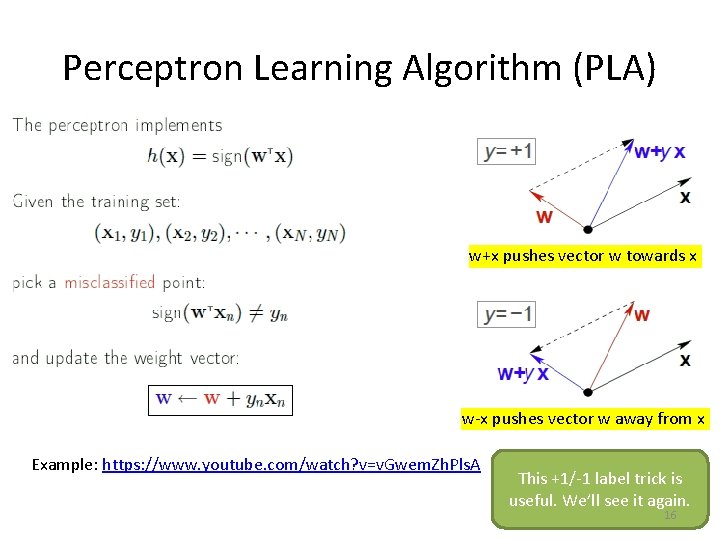
Perceptron Learning Algorithm (PLA) w+x pushes vector w towards x w-x pushes vector w away from x Example: https: //www. youtube. com/watch? v=v. Gwem. Zh. Pls. A This +1/-1 label trick is useful. We’ll see it again. 16

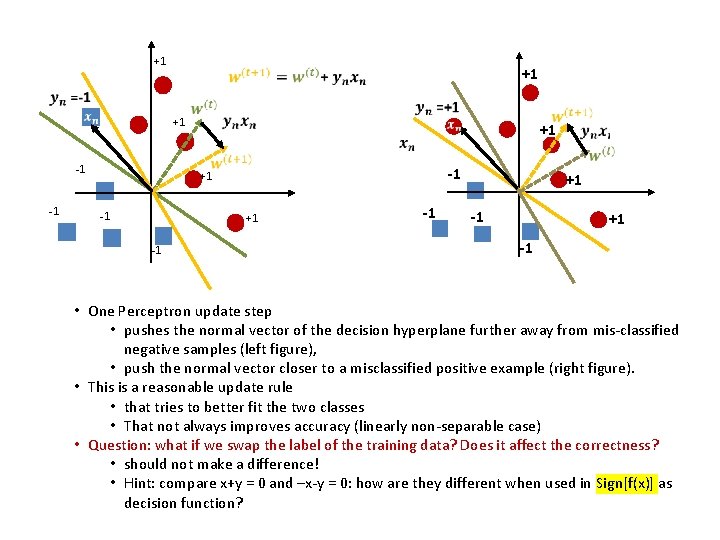
+1 +1 +1 -1 -1 +1 -1 • One Perceptron update step • pushes the normal vector of the decision hyperplane further away from mis-classified negative samples (left figure), • push the normal vector closer to a misclassified positive example (right figure). • This is a reasonable update rule • that tries to better fit the two classes • That not always improves accuracy (linearly non-separable case) • Question: what if we swap the label of the training data? Does it affect the correctness? • should not make a difference! • Hint: compare x+y = 0 and –x-y = 0: how are they different when used in Sign[f(x)] as decision function?

PLA Summary • One iteration of PLA updates the weights, w, for a misclassified point • Done when there are no misclassified points • Guaranteed to converge if data is linearly separable – What if the data is not linearly separable? 18

Example Linear Classification 19

Input Representation • Raw input: 16*16 image = 256 pixels x = (x 0, x 1, x 2, …, x 256) • Linear model: w = (w 0, w 1, w 2, …, w 256) • Features: Extract useful information from raw data – Intensity and symmetry x = (x 0, x 1, x 2) – Linear model w = (w 0, w 1, w 2) 20

Feature Space • Consider a binary classification task – “Is x a ‘ 1’ (positive) or a ‘ 5’ (negative)? ” Not linearly separable 21

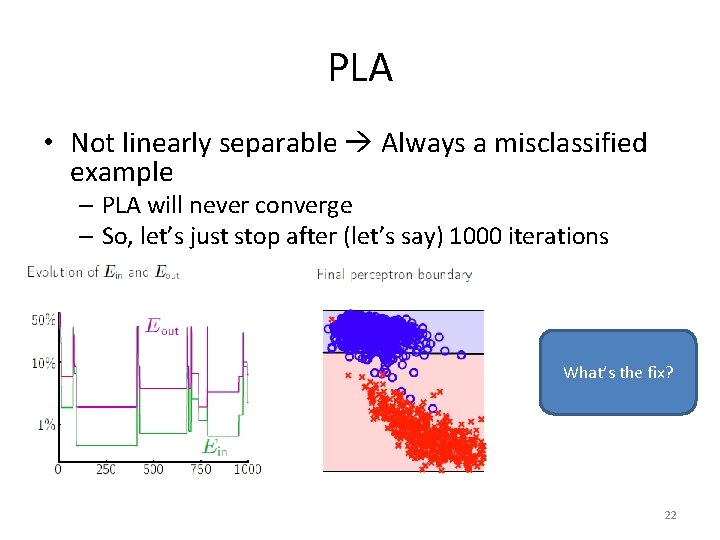
PLA • Not linearly separable Always a misclassified example – PLA will never converge – So, let’s just stop after (let’s say) 1000 iterations What’s the fix? 22

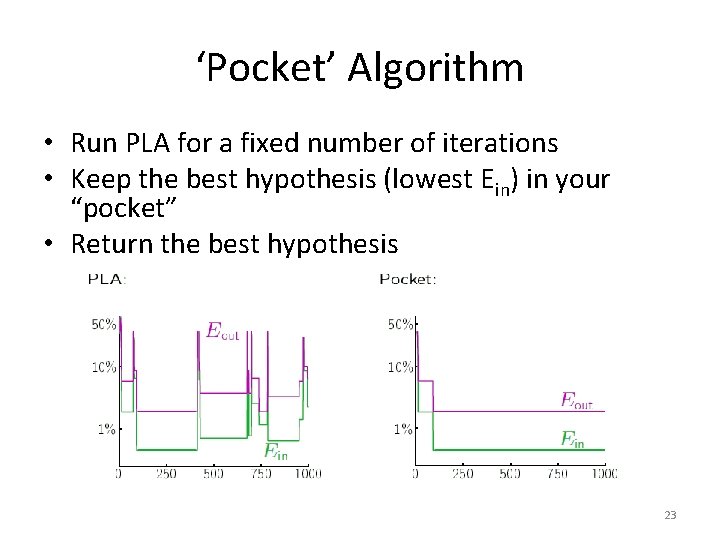
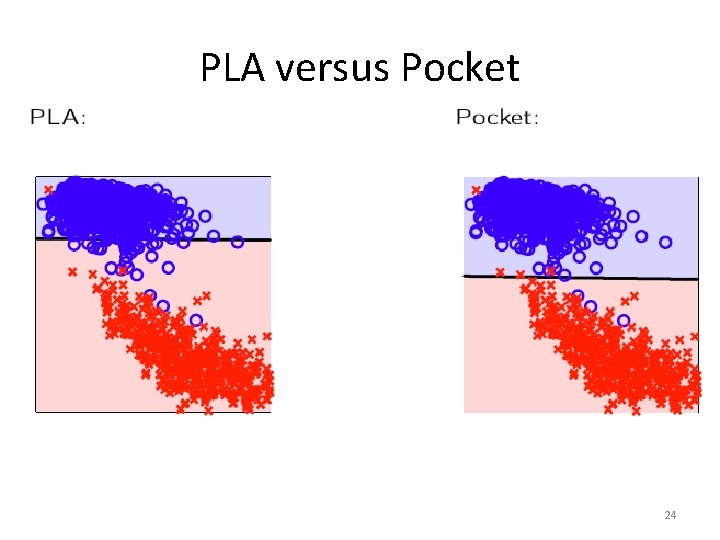
‘Pocket’ Algorithm • Run PLA for a fixed number of iterations • Keep the best hypothesis (lowest Ein) in your “pocket” • Return the best hypothesis 23

PLA versus Pocket 24

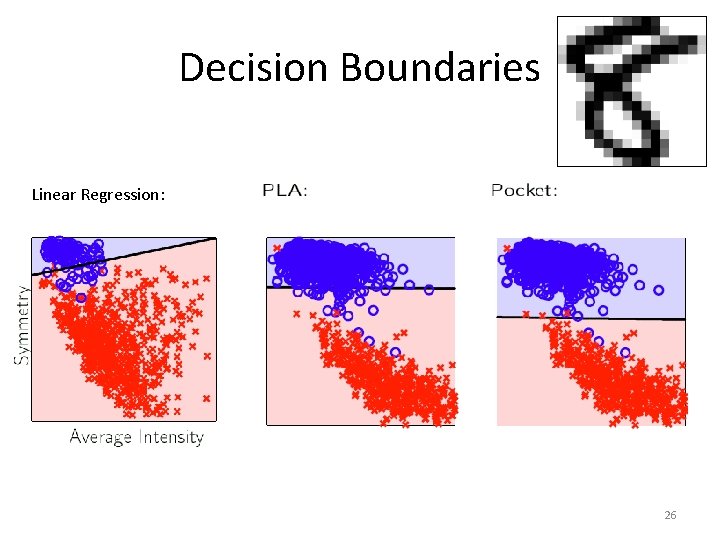
Linear Regression for Classification • Linear regression learns a real-valued function y = f(x) • Binary-valued functions are also real-valued: {+1, -1} • Use linear regression to get w where • sign(w. TXn) is likely to agree with 25

Decision Boundaries Linear Regression: 26

Recap • Linear methods – Lines, planes, hyperplanes – classification (PLA, Pocket Algorithm) – regression (pseudo-inverse) • Benefits of linear approaches – Simple algorithms – (Human) interpretable model parameters • Drawbacks – Most real-world problems are not linear 27

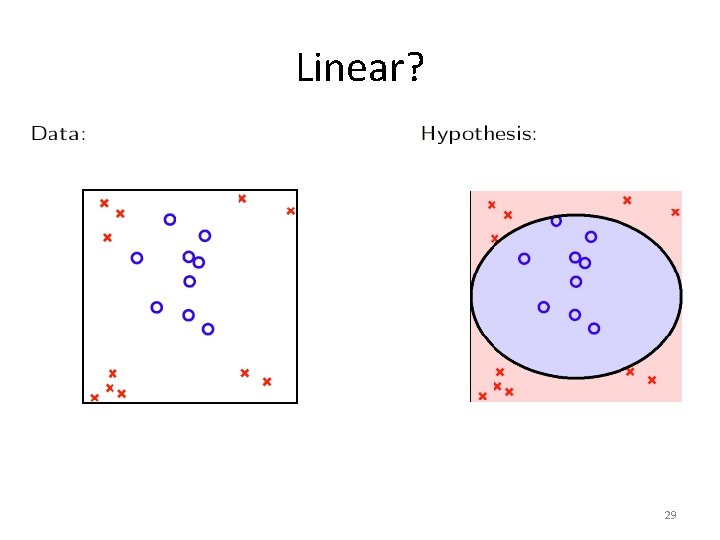
Back to Credit Example • Credit line is affected by ‘years in residence’ – But perhaps not linearly • Perhaps credit officers use a different model – Is ‘years in residence’ less than 1? – Is ‘years in residence’ greater than 5? • Can we do that with linear models? 28

Linear? 29

Linear in what? • Linear regression implements: • Linear classification implements: • What are the unknowns? • Algorithms work because of linearity in the weights 30

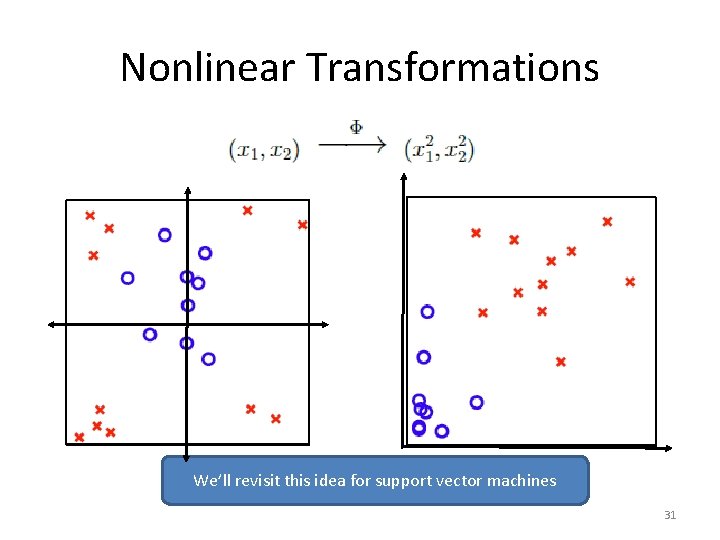
Nonlinear Transformations We’ll revisit this idea for support vector machines 31

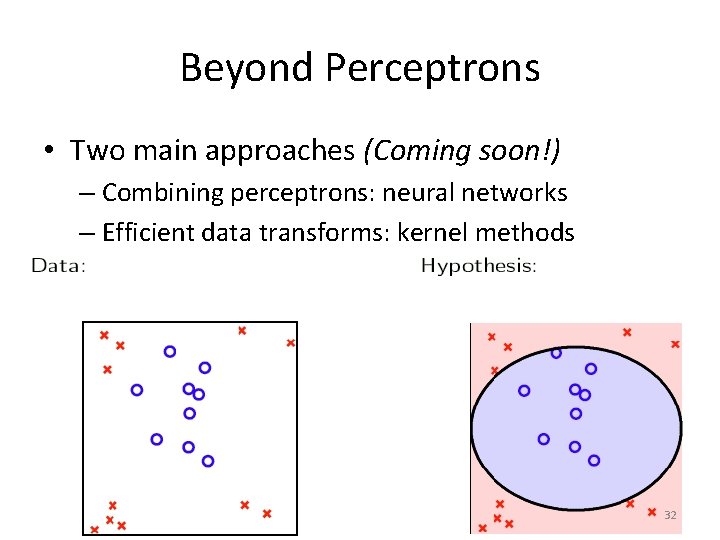
Beyond Perceptrons • Two main approaches (Coming soon!) – Combining perceptrons: neural networks – Efficient data transforms: kernel methods 32

Summary Credit Analysis • Benefits of linear approaches – Simple algorithms – (Human) interpretable model parameters • Drawbacks – Most real-world problems are not linear • Nonlinear transformations can help 33