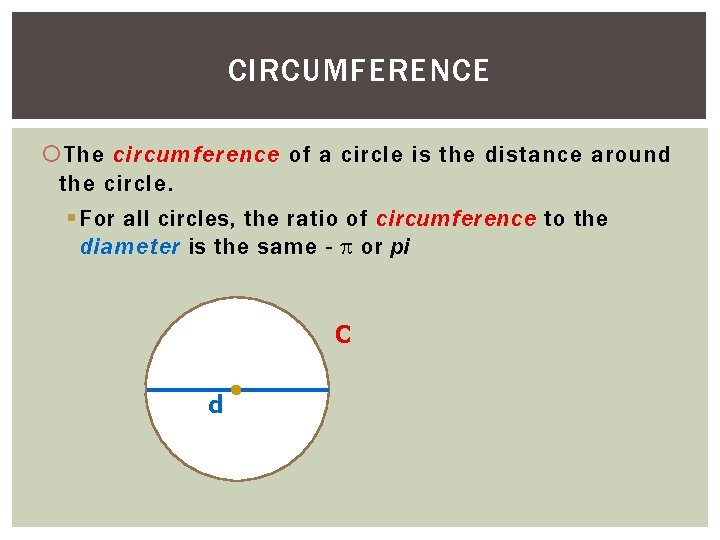
CIRCUMFERENCE The circumference of a circle is the

CIRCUMFERENCE The circumference of a circle is the distance around the circle. § For all circles, the ratio of circumference to the diameter is the same - or pi C d

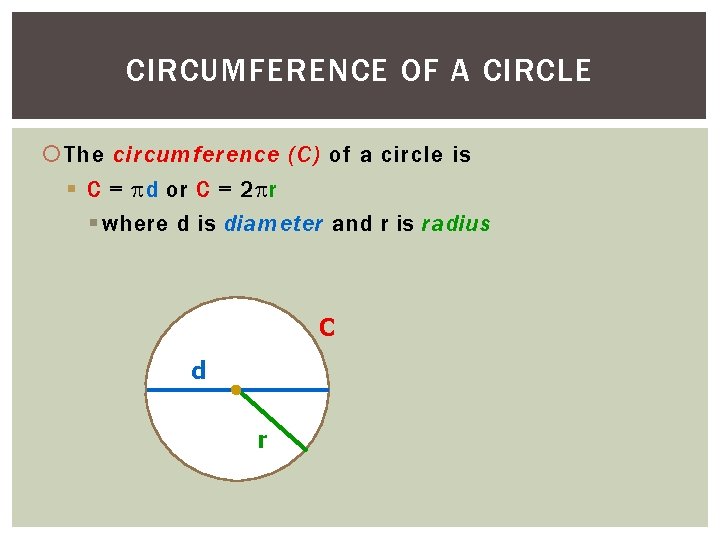
CIRCUMFERENCE OF A CIRCLE The circumference (C) of a circle is § C = d or C = 2 r § where d is diameter and r is radius C d r

USEFUL INFORMATION If asked to find the circumference. identify what you know § diameter § Use C = d § radius § Use C = 2 r If asked to find the diameter or radius, you must work backwards. § diameter § Divide by § radius § Divide by 2

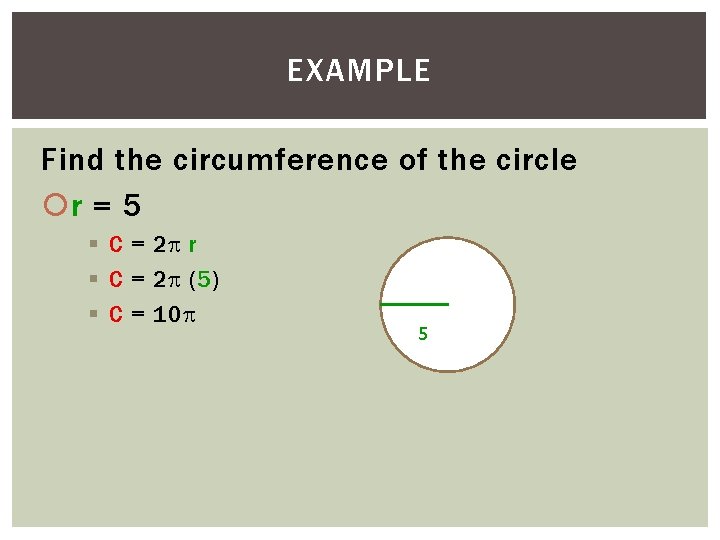
EXAMPLE Find the circumference of the circle r = 5 § C = 2 r § C = 2 (5) § C = 10 5

EXAMPLE C = 32 § Find diameter § d = C/ § d = 32 / § d = 32 32

ARC LENGTH An arc length is a portion of the circumference. It is determined by its arc measure § The measure of the angle made by joining the endpoints of the arc with the center of the circle. § denoted by placing an m in front to show we are finding the measure A AB m. AB B

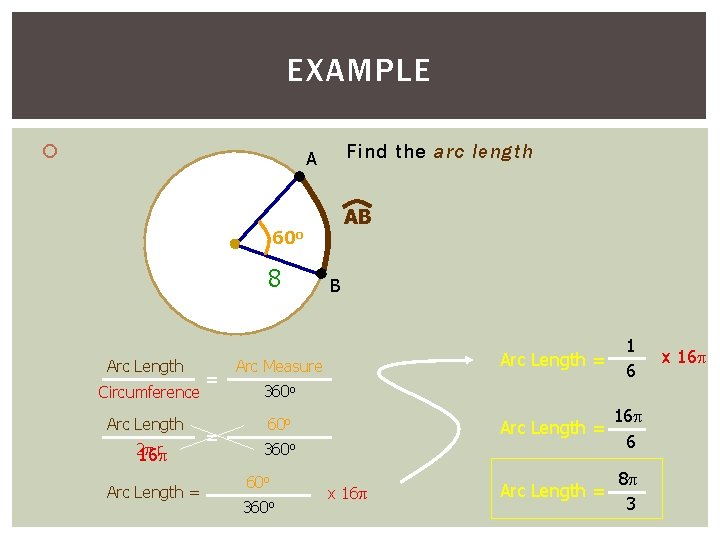
EXAMPLE Find the arc length A AB 60 o 8 Arc Length Circumference Arc Length 2 r 16 Arc Length = = = B Arc Measure Arc Length = 1 6 Arc Length = 16 6 Arc Length = 8 3 360 o 60 o 360 o x 16

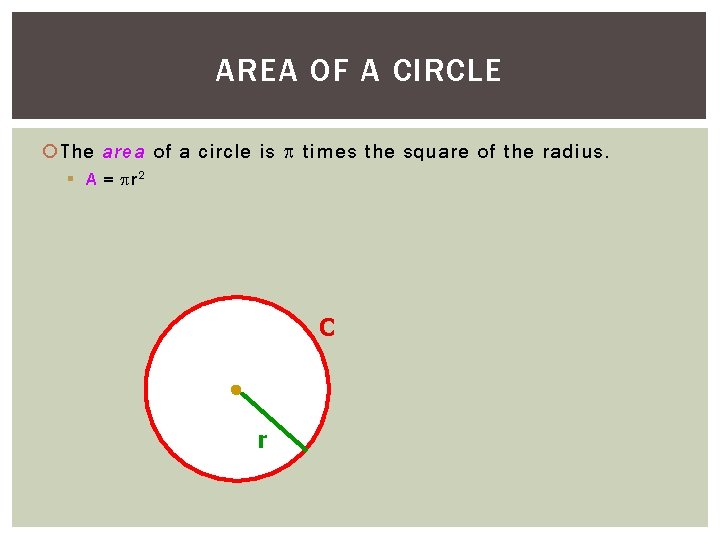
AREA OF A CIRCLE The area of a circle is times the square of the radius. § A = r 2 C r

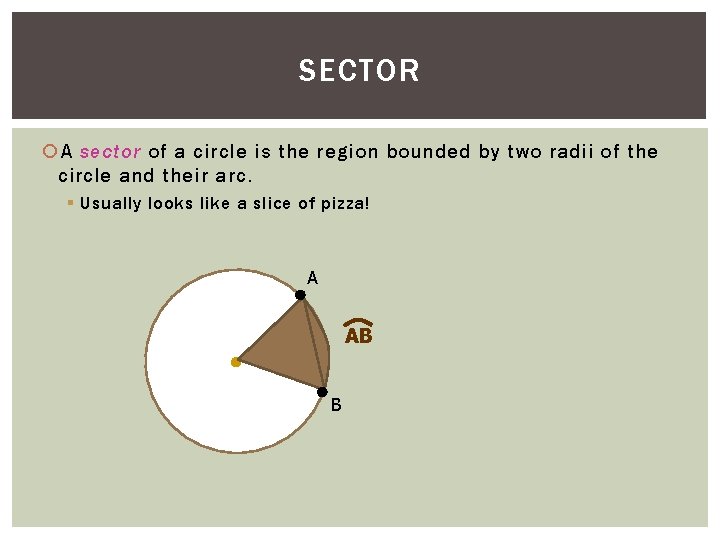
SECTOR A sector of a circle is the region bounded by two radii of the circle and their arc. § Usually looks like a slice of pizza! A AB B

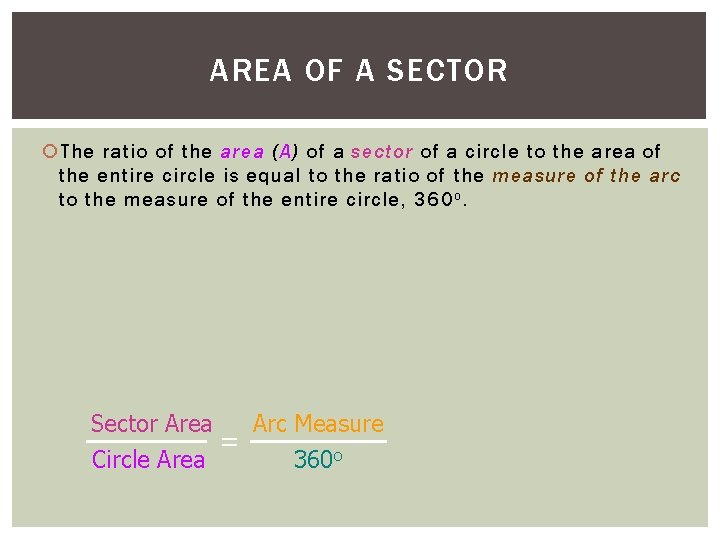
AREA OF A SECTOR The ratio of the area (A) of a sector of a circle to the area of the entire circle is equal to the ratio of the measure of the arc to the measure of the entire circle, 360 o. Sector Area Arc Measure = 360 o Circle Area

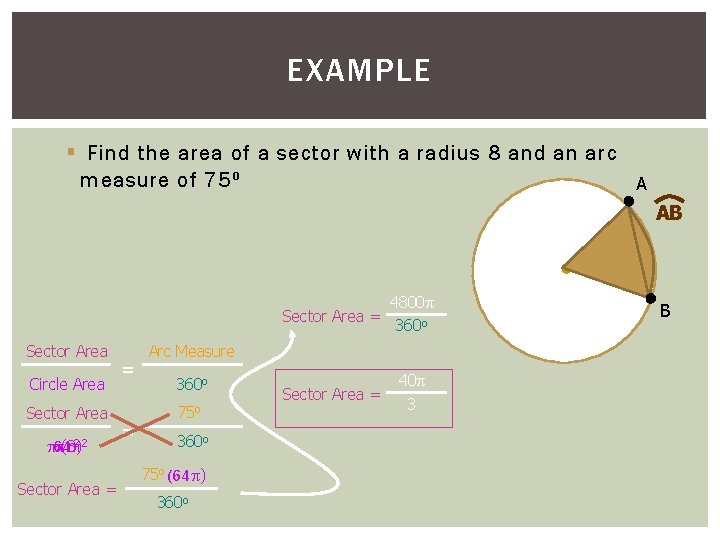
EXAMPLE § Find the area of a sector with a radius 8 and an arc measure of 75 o A AB Sector Area Circle Area Sector Area 64 (8) r 2 2 Sector Area = = = Sector Area = 4800 360 o Sector Area = 40 3 Arc Measure 360 o 75 o (64 ) 360 o B