Circular Trip An Effective Algorithm for Continuous k

Circular. Trip: An Effective Algorithm for Continuous k. NN Queries Muhammad Aamir Cheema Database Research Group, The School of Computer Science and Engineering, University of New South Wales (UNSW), Sydney Joined work with: Yidong Yuan (UNSW), Xuemin Lin (UNSW)

Problem Settings l l l Given a query point q, continuously report k nearest objects of q according to Euclidean distance Objects and query points move in an unpredictable fashion Objects and query points can be indexed in main memory

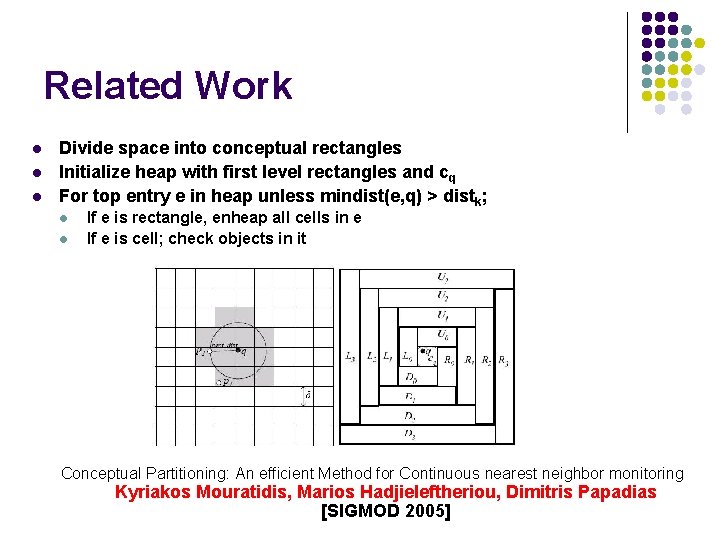
Related Work l l l Divide space into conceptual rectangles Initialize heap with first level rectangles and cq For top entry e in heap unless mindist(e, q) > distk; l l If e is rectangle, enheap all cells in e If e is cell; check objects in it Conceptual Partitioning: An efficient Method for Continuous nearest neighbor monitoring Kyriakos Mouratidis, Marios Hadjieleftheriou, Dimitris Papadias [SIGMOD 2005]

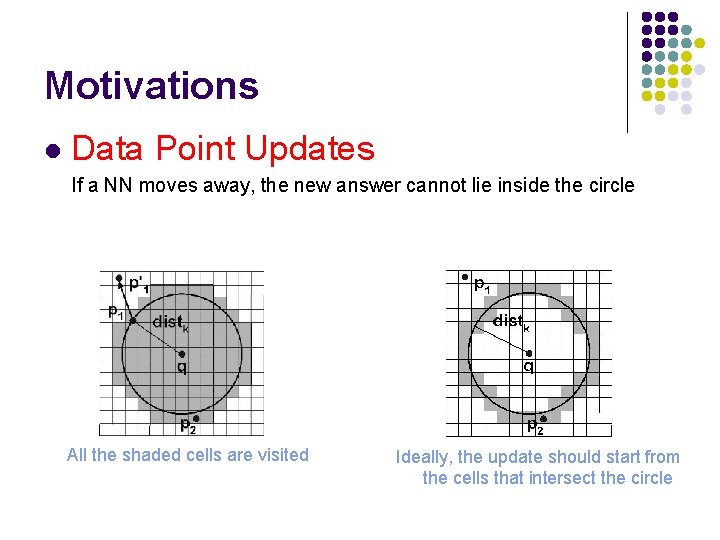
Motivations l Data Point Updates If a NN moves away, the new answer cannot lie inside the circle All the shaded cells are visited Ideally, the update should start from the cells that intersect the circle

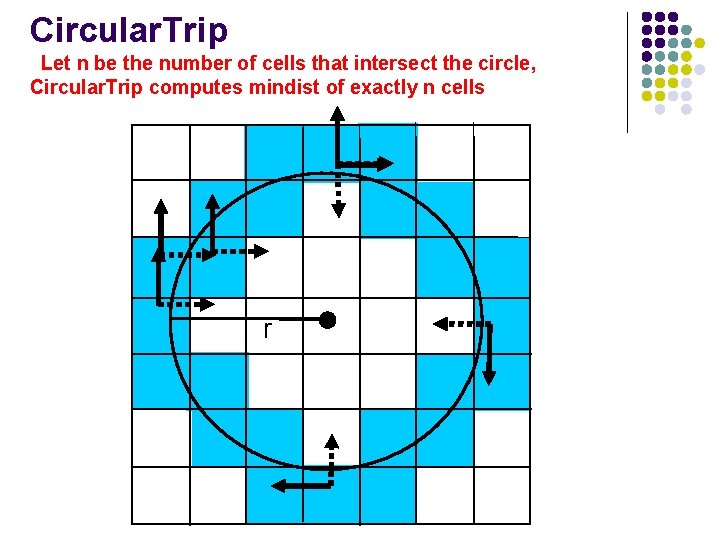
Motivations l Rectangles do not approximate circles very well All the cells in any rectangle Rec are inserted in heap when r becomes greater than mindist(Rec, q) All cells in the four rectangles are enheaped. Ideally, only the cells that intersect the circle should be enheaped How to find all the cells that intersect a given circle? Circular. Trip

Circular. Trip Let n be the number of cells that intersect the circle, Circular. Trip computes mindist of exactly n cells r

k. NN Initial Computation l l r=0, distk = ∞ (distk = distance of kth NN) Repeat unless r ≥ distk l Call Circular. Trip with radius Min(r=r+ δ, distk) (δ= cell width) l Insert returned cells into heap according to ascending order of their mindist from q l For each cell c in heap l If mindist(c, q) ≥ distk § RETURN RESULTS l Find points in c and update distk and q. k. NN accordingly r = 2. δ δ dist(p 1, q) dist(p 21, q) distk= ∞ q. k. NN = pΦ 12 p 1 r p 2 q

Continuous Monitoring l l l Incoming objects: any non-result object p entering inside the circle l Insert p into q. k. NN Outgoing objects: any result object leaving the circle l delete p from q. k. NN Hanlde all the object updates as mentioned above Case 1: q. k. NN contains k or more than k objects l Keep k closest objects and discard other Case 2: q. k. NN contains less than k objects l Same as initial computation except the starting radius is distk p 1 q distk p 2

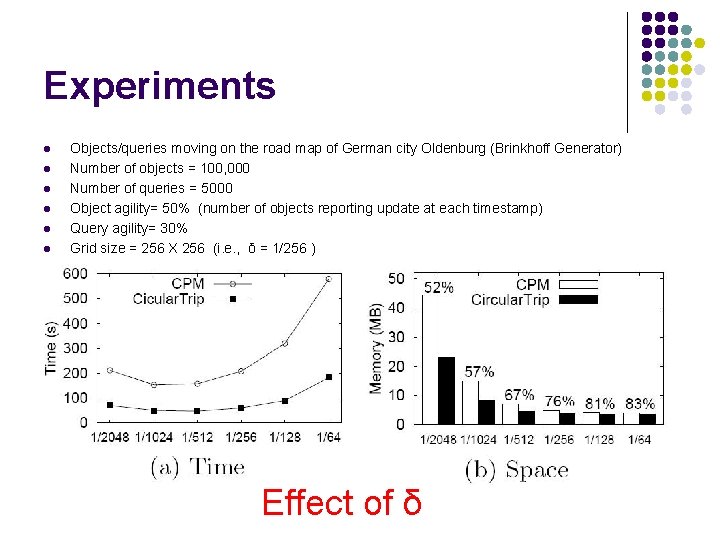
Experiments l l l Objects/queries moving on the road map of German city Oldenburg (Brinkhoff Generator) Number of objects = 100, 000 Number of queries = 5000 Object agility= 50% (number of objects reporting update at each timestamp) Query agility= 30% Grid size = 256 X 256 (i. e. , δ = 1/256 ) Effect of δ

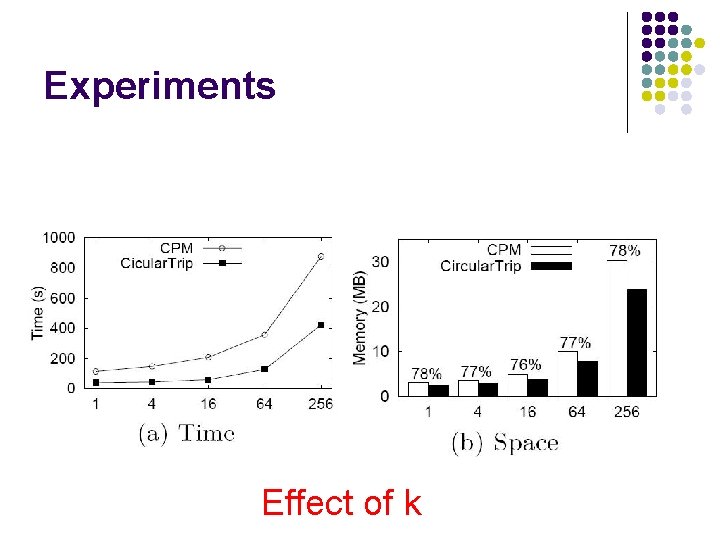
Experiments Effect of k

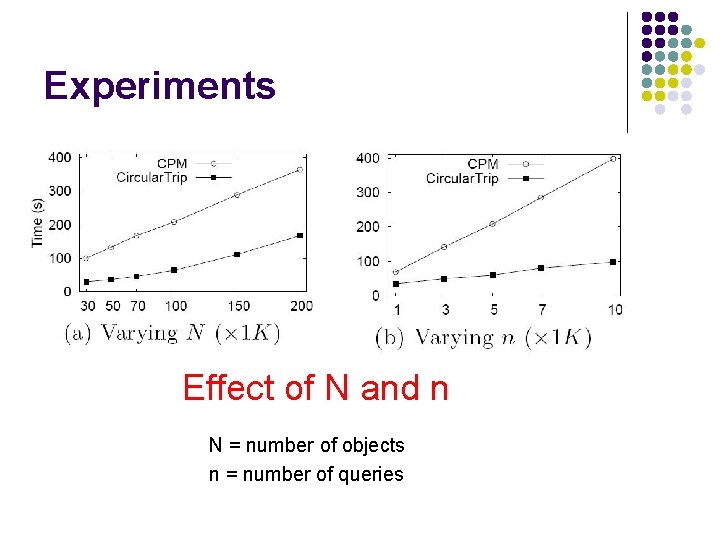
Experiments Effect of N and n N = number of objects n = number of queries

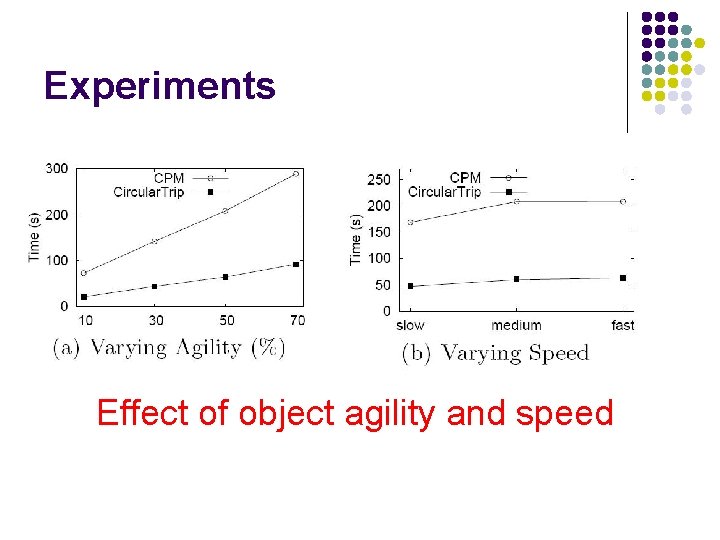
Experiments Effect of object agility and speed

Questions

Space Usage l CPM stores visit list and heap for each query