Circular Motion The Radian The radian is angle













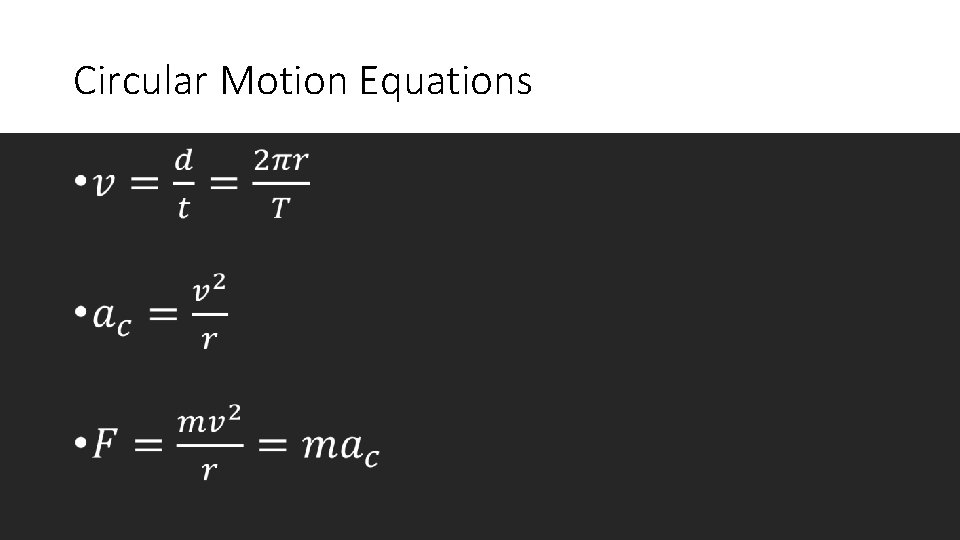




- Slides: 22

Circular Motion

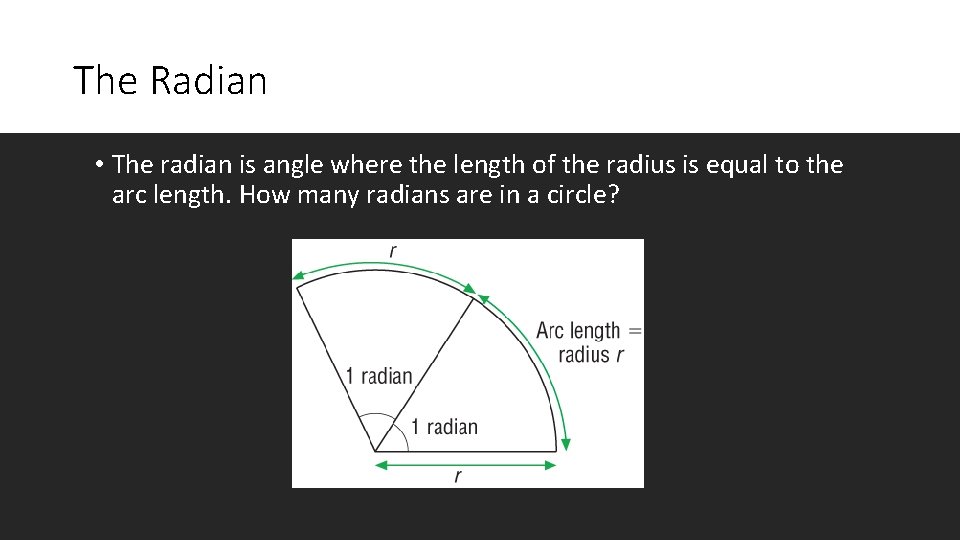
The Radian • The radian is angle where the length of the radius is equal to the arc length. How many radians are in a circle?

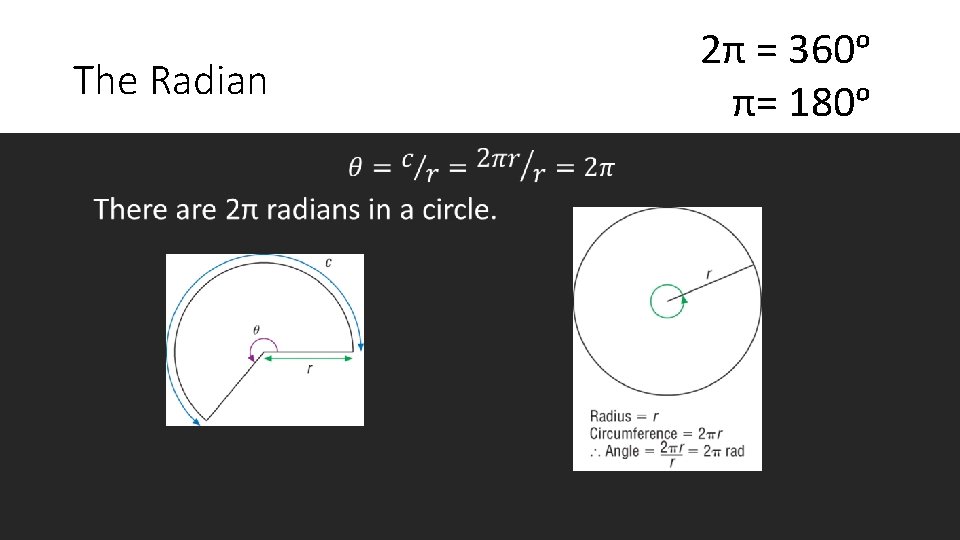
The Radian • 2π = 360ᵒ π= 180ᵒ

Conversion • Convert these from degrees to radians or vice versa.

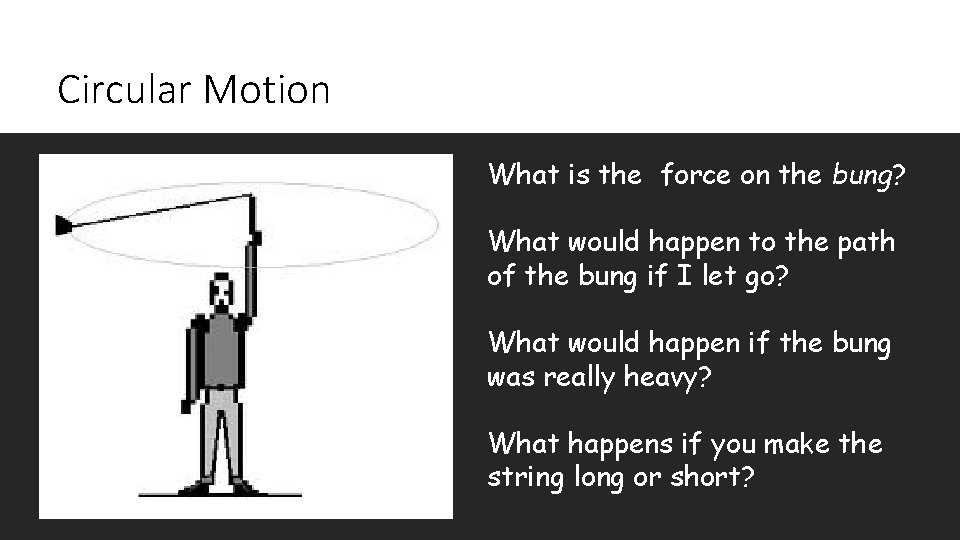
Circular Motion What is the force on the bung? What would happen to the path of the bung if I let go? What would happen if the bung was really heavy? What happens if you make the string long or short?

Circular Motion • An object in circular motion is constantly changing direction. • Therefore, it must be accelerating. • That means a force must be present. • The centripetal force acts towards the center of the circle and maintains circular motion.

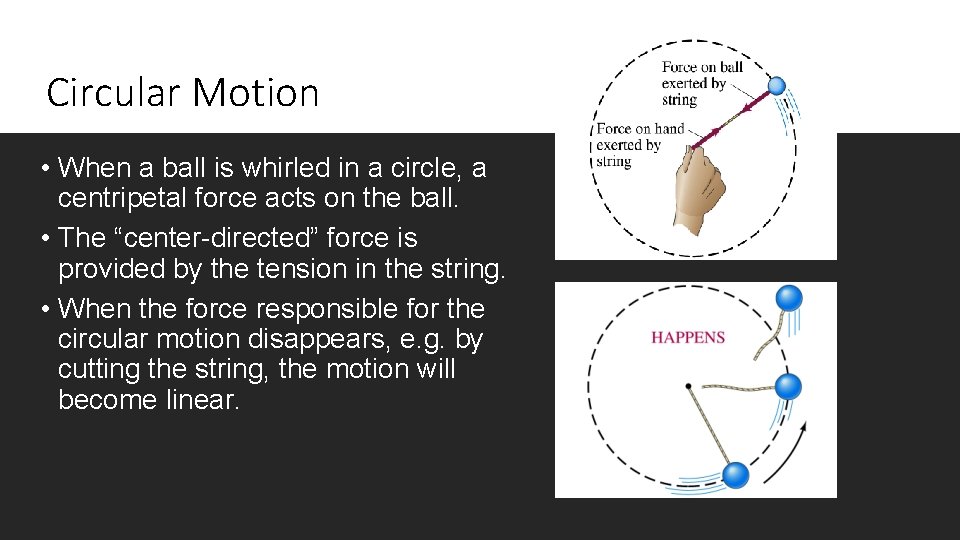
Circular Motion Example Circular Motion • When a ball is whirled in a circle, a centripetal force acts on the ball. • The “center-directed” force is provided by the tension in the string. • When the force responsible for the circular motion disappears, e. g. by cutting the string, the motion will become linear.

Circular Motion Centripetal Acceleration CENTRIPETAL ACCELERATION The equation for centripetal acceleration is: Centripetal acceleration always points to the center of the circle. Its magnitude is equal to the square of the speed, divided by the radius of motion.

CENTRIPETAL ACCELERATION To analyze centripetal acceleration situations accurately, you must identify the agent of the force that causes the acceleration. Then you can apply Newton’s second law for the component in the direction of the acceleration in the following way. Newton’s Second Law for Circular Motion

Centripetal Force Friction Gravity What provides the centripetal force in each case ? Opposite charge

Circular Motion If the force is toward the center of the circle, why do you seem to be thrown outward when a car rounds a curve? According to Newton’s first law, you will continue moving with the same velocity unless there is a net force acting on you. The passenger in the car would continue to move straight ahead if it were not for the force of the door acting in the direction of the acceleration. The so-called centrifugal, or outward force, is a fictitious, nonexistent force.

What keeps bodies moving in a circle? • When a body moves in a circle it continuously accelerates towards the centre of the circle. This acceleration changes the direction of motion of the body, not its speed. • The resultant force causing this acceleration is called the centripetal force. • The direction of the centripetal force is always towards the centre of the circle. • The centripetal force needed to make a body perform circular motion increases as: − the mass of the body increases; − the speed of the body increases; − the radius of the circle decreases.

What provides the centripetal force for planets and satellites? • The centripetal force that allows planets and satellites to maintain their circular orbits is called gravity. • The bigger the masses of the bodies the bigger the force of gravity between them. • As the distance between two bodies increases the force of gravity between them decreases. • The further away an orbiting body is the longer it takes to make a complete orbit. • To stay in orbit at a particular distance, planets and satellites must move at a particular speed around larger bodies.

What provides the centripetal force for planets and satellites? • Communications satellites are usually put into a geostationary orbit above the equator. • Monitoring satellites are usually put into a low polar orbit.

What keeps bodies moving in a circle? • When a body moves in a circle it continuously accelerates towards the centre of the circle. This acceleration changes the direction of motion of the body, not its speed. • The resultant force causing this acceleration is called the centripetal force. • The direction of the centripetal force is always towards the centre of the circle. • The centripetal force needed to make a body perform circular motion increases as: − the mass of the body increases; − the speed of the body increases; − the radius of the circle decreases.

What provides the centripetal force for planets and satellites? • The centripetal force that allows planets and satellites to maintain their circular orbits is called gravity. • The bigger the masses of the bodies the bigger the force of gravity between them. • As the distance between two bodies increases the force of gravity between them decreases. • The further away an orbiting body is the longer it takes to make a complete orbit. • To stay in orbit at a particular distance, planets and satellites must move at a particular speed around larger bodies.

What provides the centripetal force for planets and satellites? • Communications satellites are usually put into a geostationary orbit above the equator. • Monitoring satellites are usually put into a low polar orbit.
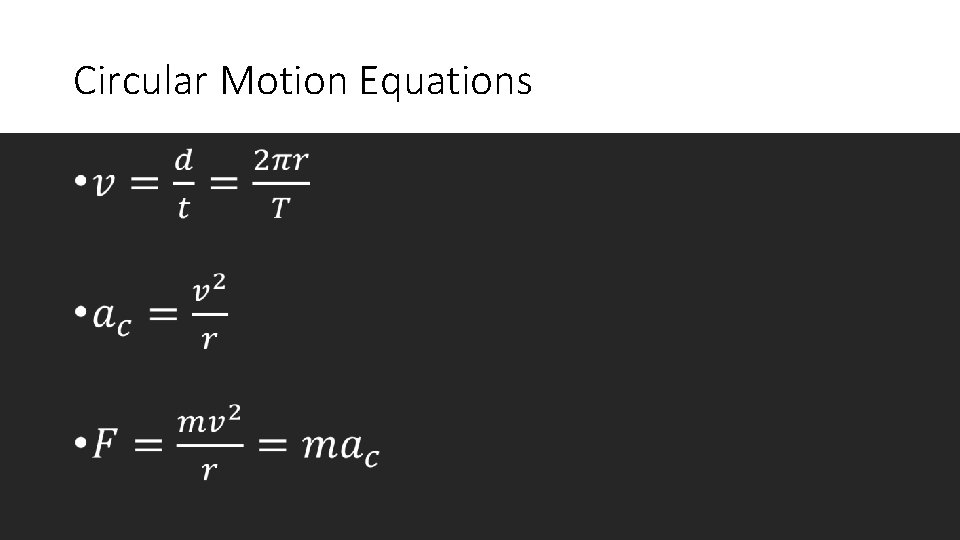
Circular Motion Equations •

Circular Motion Practical Write-up

Your results: 1. Ensure you have a full set of results, preferably with repeats. 2. If you have repeat results calculate average values for t (the time taken for 10 swings) 3. Calculate T (the time take for one swing = t/10) 4. Calculate the total displacement, s, for 1 swing (s = 2πr where r is the radius) 5. Now calculate the velocity, v = s/T 6. Almost there…. calculate the acceleration, a = v 2/r 7. Finally, calculate the centripetal force using Newton’s 2 nd Law…. . F = ma, where m is the mass

Your graphs: • You have 2 graphs to plot: • F vs a and v 2 vs a (put a on the x-axis for both graphs!) • *plot the graphs on 2 separate pieces of graph paper* Remember your rules for graphs: ØUse sensible scales (don’t go up in 3 s, 6 s, 7 s or 9 s), your graphs must take up 75% of the A 4 page…. it doesn’t count if your trim the edges! ØPlot your points accurately ØLabel the axis and give the graph a title ØDraw a line/curve of best fit

Analysis • 1. Describe the relationship for each graph. Calculate the gradient for each. What do the gradients of each graph represent? (Hint: look at the units for Δy/Δx, then examine your data. ) • *When calculating the gradient, use the triangle method ensuring the hypotenuse is at least half the length of your line of best fit* 2. Describe how adjustments in the radius r would affect the masses velocity given the same Fc. 3. Describe some ways in which the method could be improved in order to improve the accuracy of your measurements if you were to do the practical again