Circular Motion Gravity Chapter 7 Circular Motion Objects

Circular Motion & Gravity Chapter 7

Circular Motion • Objects travel in a circle • Rotate about an axis of rotation • Tangential speed (vt) describes the rate at which the object moves around the circle • Direction is tangential to the circular path
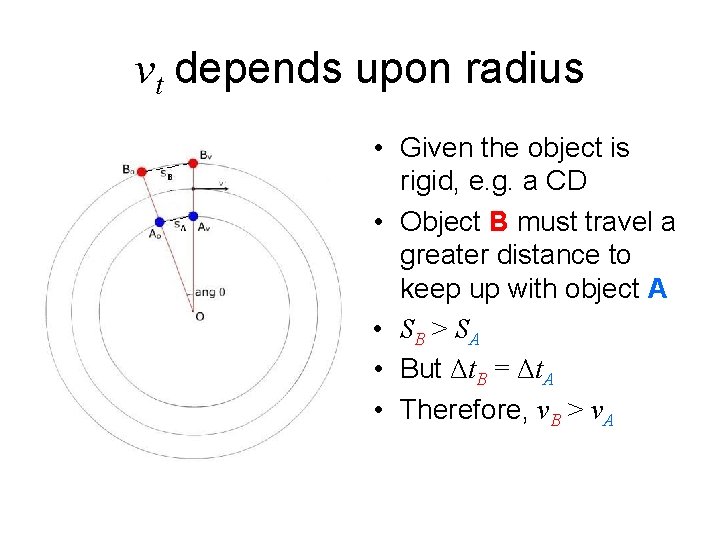
vt depends upon radius • Given the object is rigid, e. g. a CD • Object B must travel a greater distance to keep up with object A • SB > SA • But Δt. B = Δt. A • Therefore, v. B > v. A

Comparison of Translational Motion & Uniform Circular Motion UCM = motion of an object traveling in a circle at a constant speed, vt Type of Motion Translational Displacement Linear Δx Time Δt Formula vavg = Δx/Δt Uniform Circular Circumference 2πr Period T vt = 2πr/T

Uniform Circular Motion • Tangential speed vt is constant • Because direction is changing, there is acceleration • Centripetal acceleration
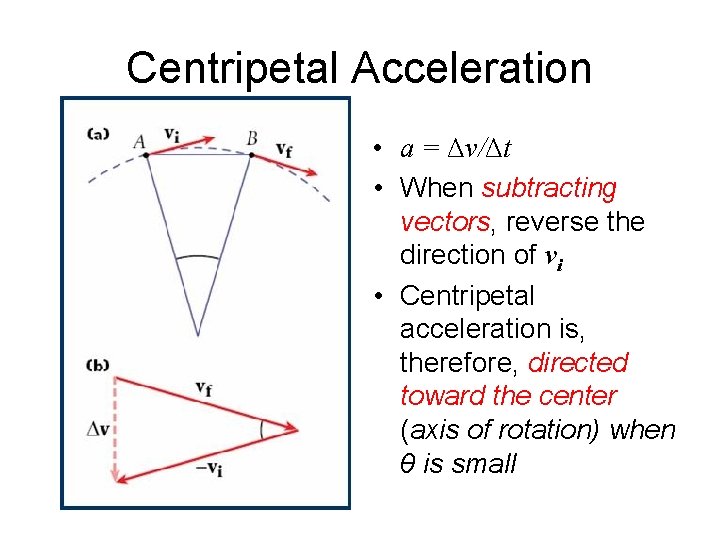
Centripetal Acceleration • a = Δv/Δt • When subtracting vectors, reverse the direction of vi • Centripetal acceleration is, therefore, directed toward the center (axis of rotation) when θ is small

Centripetal Acceleration • Centripetal means “center seeking” and is always directed toward the center • Due to a change in direction of vt • Phet simulation
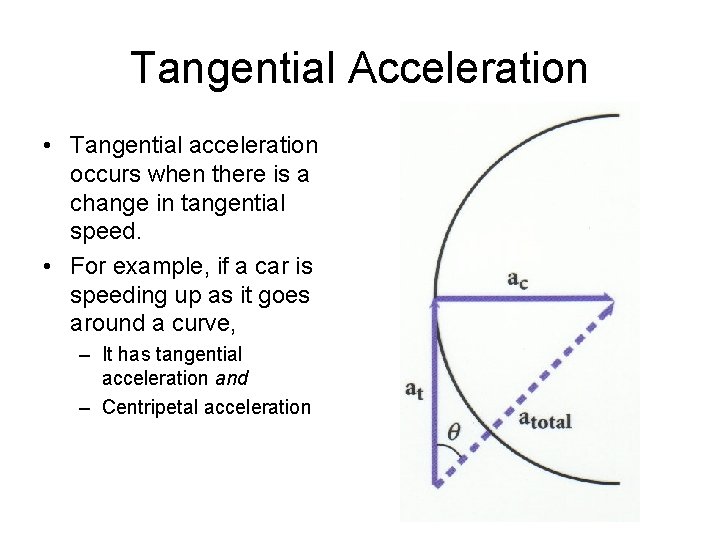
Tangential Acceleration • Tangential acceleration occurs when there is a change in tangential speed. • For example, if a car is speeding up as it goes around a curve, – It has tangential acceleration and – Centripetal acceleration
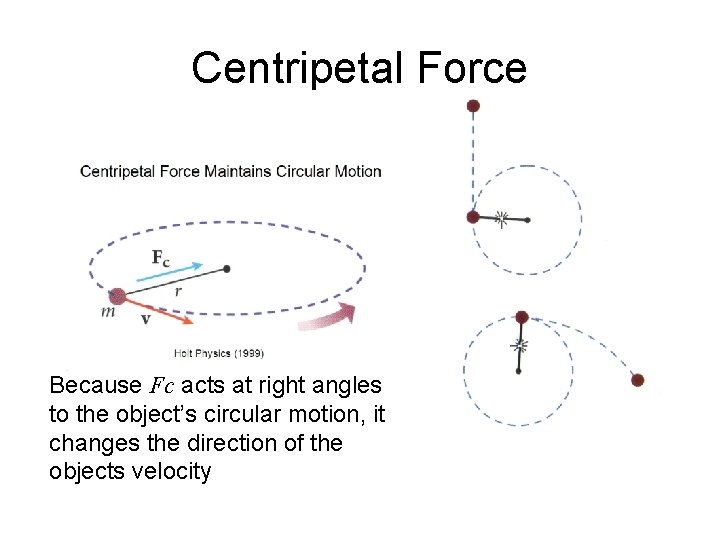
Centripetal Force Because Fc acts at right angles to the object’s circular motion, it changes the direction of the objects velocity

Centripetal Force • Is the cause of centripetal acceleration • It is directed toward the axis of rotation • It is the net force acting on an object in uniform circular motion, i. e. it is the cause of circular motion • Centrifugal force is a misunderstanding of inertia

Centripetal Force & Newton’s 2 nd Law

Centripetal Force • Is just the name of any net force acting on an object in uniform circular motion • Fc could take any form…. • It could be frictional force, tension force, gravitational force, etc.
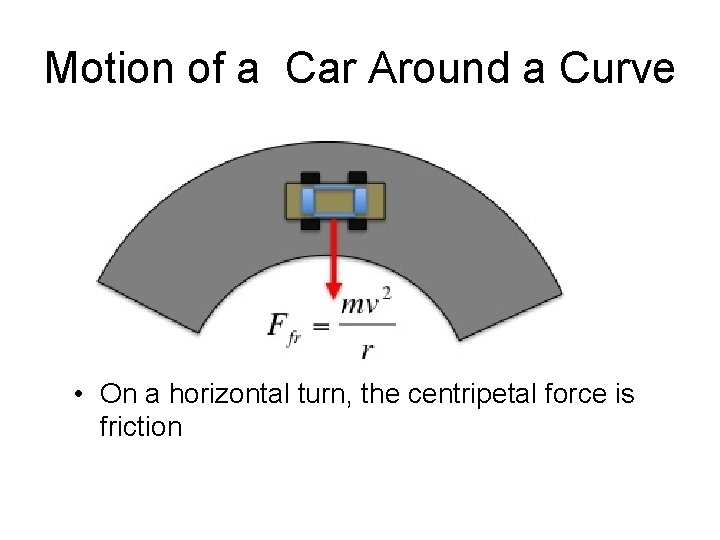
Motion of a Car Around a Curve • On a horizontal turn, the centripetal force is friction
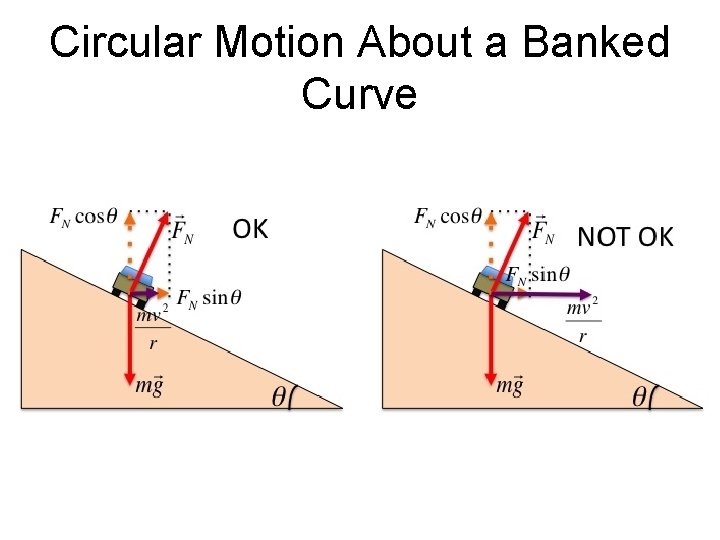
Circular Motion About a Banked Curve
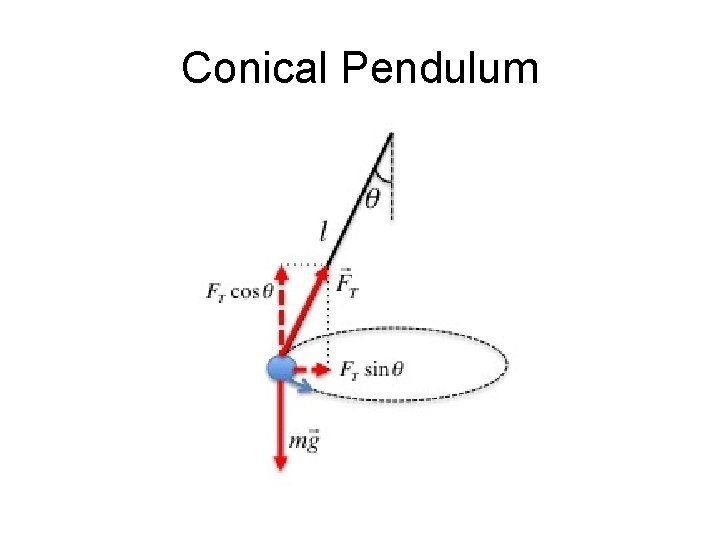
Conical Pendulum
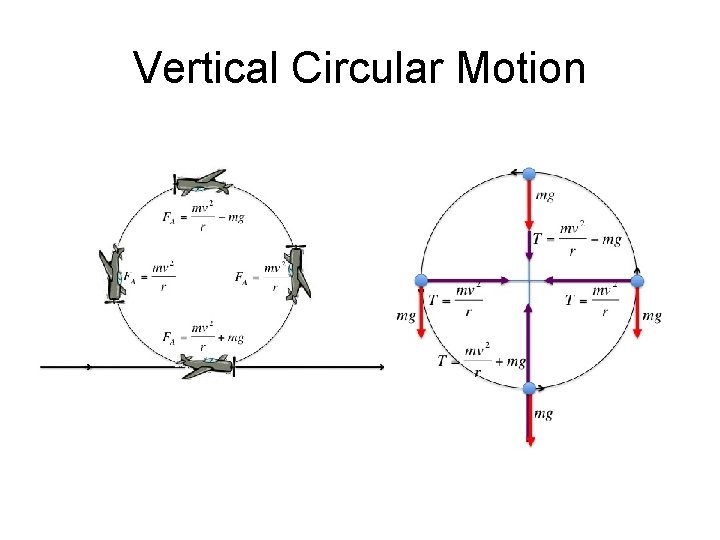
Vertical Circular Motion

Centrifugal Force? • If Fc is insufficient to maintain circular motion, the object will leave it’s circular path due to its own inertia, not because some force is pulling it away from the axis of rotation • Thus, inertia is often mistaken for “centrifugal force”

Gravity

Gravitational Force • • • Force of attraction between two masses Attractive only One of four fundamental forces Very weak (the weakest) When one object orbits another, gravitational force is a centripetal force

Newton’s Law of Universal Gravitation • Gravitational force is… – directly proportional to the product of the masses of the two bodies – inversely proportional to the square of the distance between the centers of the two masses – If the objects are large (e. g. planets, moons) then the radii would be included in r
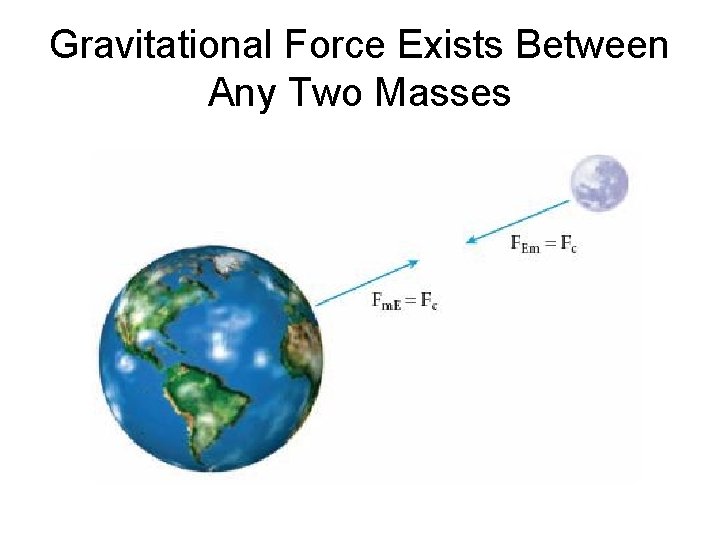
Gravitational Force Exists Between Any Two Masses

Newton’s Cannon http: //spaceplace. nasa. gov/en/kids/orbits 1. shtml http: //galileoandeinstein. physics. virginia. edu/more_stuff/Applets/Newt Mtn/home. html

Importance of Gravitational Force • Keeps you from floating away into space • Gravitational force keeps the Moon and planets in orbit • Keeps earth in orbit around sun • Causes ocean tides

Black Holes: Extreme Gravity Extreme density Escape velocity > speed of light Detect by effects on surrounding matter

Gravitational Field Strength • Increases as distance from mass center decreases • Because gravitational field strength varies, weight varies with location

Gravitational Field Strength • Describes the amount of gravitational force per unit mass at any given point • Equals free-fall acceleration

Weight Changes with Location • Because gravitational field strength varies, ag varies (acceleration of gravity). • Since w = mag, weight must vary as ag varies • Fg is an example of an inverse square law
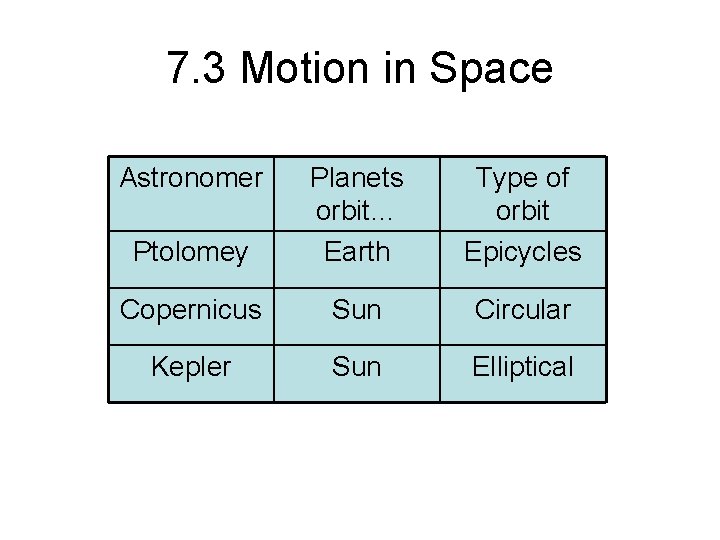
7. 3 Motion in Space Astronomer Ptolomey Planets orbit… Earth Type of orbit Epicycles Copernicus Sun Circular Kepler Sun Elliptical

Kepler’s Laws of Planetary Motion 1. The Law of Orbits: All planets move in elliptical orbits, with the sun at one focus. 2. The Law of Areas: A line that connects a planet to the sun sweeps out equal areas in equal times. 3. The Law of Periods: The square of the period of any planet is proportional to the cube of the average distance from the sun,

Kepler’s st 1 Kepler's Law Simulation and nd 2 Laws

Kepler’s 3 rd Law Describes Orbital Period

Actual and Apparent Weight • A bathroom scale records the normal force of scale acting on your body • Step on the scale … the normal force equals your weight

Actual and Apparent Weight • Now try this • Step on the scale and have someone press down on your shoulders – Predict and explain the result • Step on the scale and have someone lift you slightly • Predict and explain the result

Actual and Apparent Weight • How does this relate to your experiences in an elevator? • What would the scale read if, in an elevator, it descended with an acceleration of g?
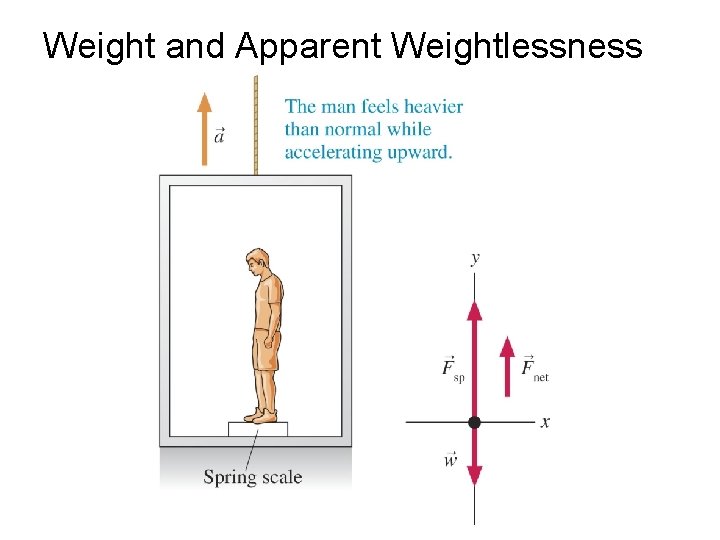
Weight and Apparent Weightlessness

Torque • a quantity that measures the ability of a force to rotate an object about an axis • “rotating ability” • Is not a force, but… • the product of force and “lever arm” • τ = F · d sinθ • Lever arm (d) is distance perpendicular to direction of force to axis of rotation
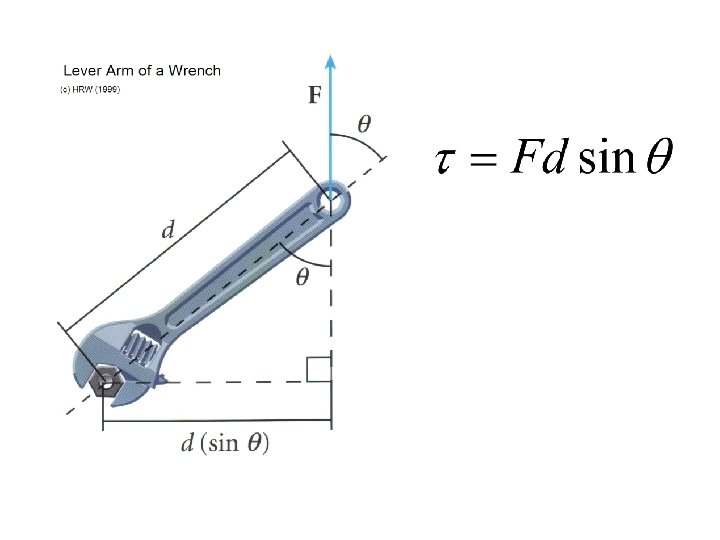

Torque • Sign (+) is counterclockwise (-) is clockwise • Net Torque and when 2 or more forces act to rotate the same object, τnet = Στ τnet = τ1 + τ2 = F 1 d 1 + F 2 d 2

Torque Equilibrium • Torque Equilibrium: Στ = 0
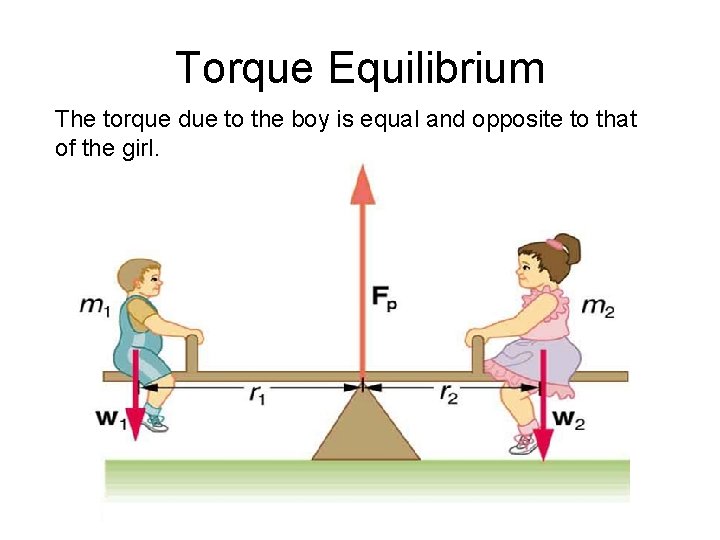
Torque Equilibrium The torque due to the boy is equal and opposite to that of the girl.
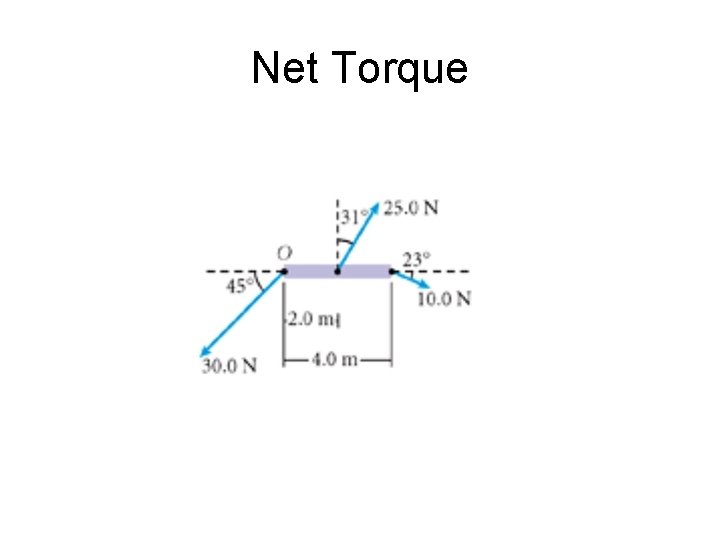
Net Torque

Center of Mass (COM) • Point mass vs. extended object • The point in a body at which all the mass can be considered to be concentrated when analyzing translational motion • Unless an object rotates about a fixed point, (e. g. a hinge)… – The point about which a mass or system of mass rotates during rotational motion

Center of Mass • The extended object rotates about the Co. M • Co. M follows the expected parabolic path
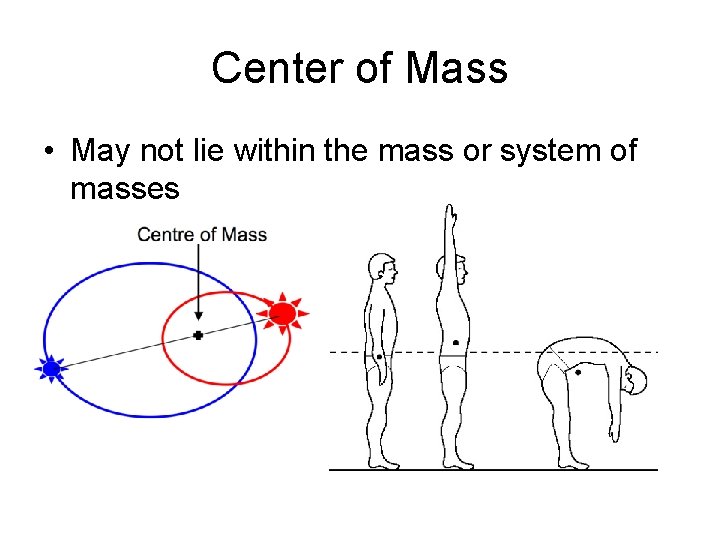
Center of Mass • May not lie within the mass or system of masses

Simple Machines • All machines are combinations of simple machines • Purpose is to change magnitude or direction of an input force • Mechanical Advantage describes the ratio of output and input forces

Ideal vs. Actual Mechanical Advantage • Ideal MA MA if there were no friction • Actual MA MA that takes friction into account

Machines and Work • Machines do not change the amount of work • Machines make work easier

Efficiency • A measure of how well a machine works • A less efficient machine produces less output per input • A less efficient machine requires more input to get the same output
- Slides: 48