Circular Motion Circular motion requires an inward force

Circular Motion

Circular motion requires an inward force • Examples – Water in bucket – Ball on string – Motorcycle in motordrome -road on car -car door on driver -Earth on moon – Bucket on water – Tension of string door – Normal force from track -friction from road -normal force from • Inward forces for above are -gravity • These forces are said to be in the centripetal direction and thus centripetal forces

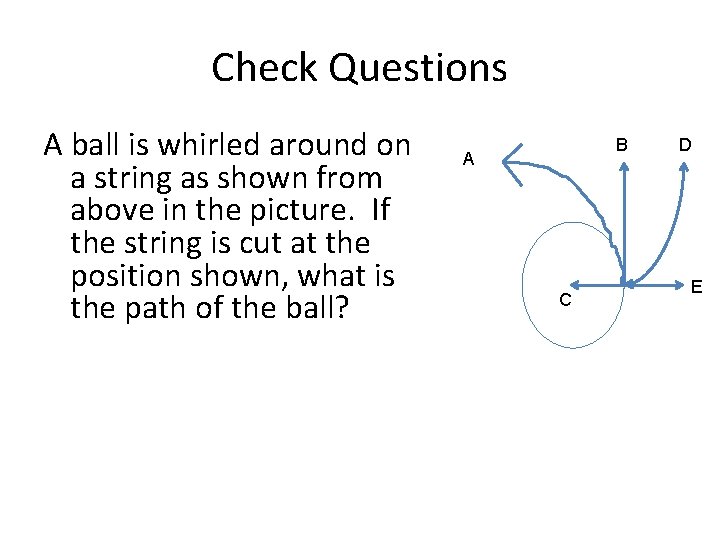
Check Questions A ball is whirled around on a string as shown from above in the picture. If the string is cut at the position shown, what is the path of the ball? B A C D E

Inward force causes change in direction but not speed. • Examples – Water in bucket – Ball on string – Motorcycle in motordrome -road on car -car door on driver -Earth on moon • Centripetal or inward force in all of these examples is perpendicular to direction object is traveling at that moment. • These centripetal forces cannot do work on moving object and the speed will remain constant. • Inward or centripetal force changes direction of object but not speed.

Check Question • A block of ice slides along a smooth surface. Will forces in the following directions affect the speed, direction or both of the block? 1. Force is in same direction of motion 2. Force is in opposite direction of motion 3. Force is perpendicular to direction of motion a) Direction only is affected b) Speed only c) Speed and direction

The magnitude of the inward force depends on the mass, radius of curvature, and velocity • Centripetal force increases proportionally w/ mass made to move in circle • Centripetal force increases as the square of the tangential speed • Centripetal force decreases linearly w/ increase of radius of curvature • Fcentripetal = mass x tangential velocity 2/ radius =mv 2/r where v 2/r is sometimes called the centripetal acceleration. • Just Newton’s 2 nd law w/ a special acceleration

Check Question • A ball is whirled on the string in a horizontal circle. Which of the following changes will increase the centripetal force needed to keep the ball moving in a circle? a) Increasing the speed the ball is whirled b) Increasing the mass of the ball c) Increasing the radius of the circle the ball is making d) A and B only e) All of these

Centrifugal Farce • Centrifugal force would be a center fleeing or outward force • Bug whirled around in can example – Thrown to outside – Bug will claim that force is acting on it but outside viewer knows bug is simply following inertial path • Centrifuge example – Separates materials according to its inertia/mass – Should be called an inertiafuge! • In above cases there is no interaction thus no outward force Centrifugal force

Artificial Gravity on Space Station • Bug in spinning tire – Faster spin means thrown against wall harder – Larger tire means thrown against wall softer – In center of axle, bug will simply rotate and not be thrown at all • For rotating circular space station – Faster spin means you would gain “weight” – As move toward center you would lose “weight”, at center you’re weightless

Odds and Ends • Tangential vs rotational or angular speed – Tangential speed is a linear speed measured in meters/ second and the like – Angular speed is measured in radians/second – Tangential speed increases as move away from center, angular speed remains constant • Centripetal vs. angular acceleration – Centripetal acceleration is a linear acceleration measured in m/s/s and directed towards the middle of the circle (a=v 2 /r)