CIRCULAR MOTION CIRCULAR MOTION Objects will continue to

CIRCULAR MOTION

CIRCULAR MOTION Objects will continue to move with a constant velocity unless acted upon by a net force. A constant net force applied perpendicular to the motion of an object will cause the object to travel a curved or circular path.

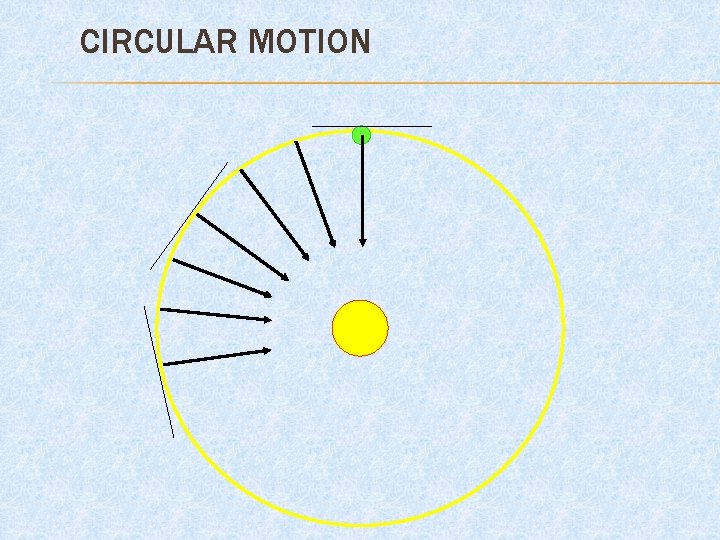
CIRCULAR MOTION

ROTATIONAL MOTION - TERMS Rotating - turning about an internal axis Axis - straight line through which rotational motion occurs Revolving - turning about an external axis Axis

TERMS Frequency – ƒ - the number of revolutions or rotations per unit of time # of occurrences in given time Units - Hertz - Hz – cycles/second Period – T - the time it takes to complete one revolution or rotation time for one occurrence Units -Seconds – seconds/cycle Period (T)= 1/ ƒ Frequency (ƒ)= ƒ) 1/ T

SPEED Linear Speed Distance traveled in a given time Ex: Miles per hour, meters per second Rotational Speed (angular speed) Cycles completed in a given time Ex: Revolutions per minute, rotations per hour

Which horse has a larger linear speed on a merry go round, one on the outside or one on the inside? Outside. Which horse has a greater rotational speed? Neither, all the horses complete the circle in the same amount of time.

ROTATIONAL MOTION - SPEED Rotational Speed - All points on a rigid rotating object have the same rotational speed Tangental (linear) Speed – Points further from the axis have greater linear speed Consider an object moving in a circle Distance around the circle is 2πr Time to complete one rotation is the period T v=d/t or v=2πr/T

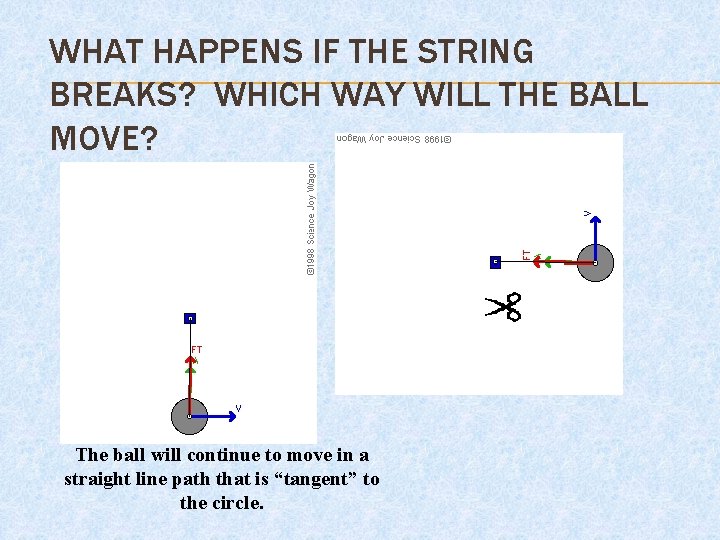
WHAT HAPPENS IF THE STRING BREAKS? WHICH WAY WILL THE BALL MOVE? The ball will continue to move in a straight line path that is “tangent” to the circle.

CIRCULAR MOTION - APPLYING NEWTON’S LAWS A change in direction is an acceleration An acceleration towards the center of a curve is called centripetal acceleration The force causing the acceleration is called centripetal force Centripetal – center seeking ac=v 2/r Fc =mv 2/r

EXAMPLE A boy twirls a 0. 5 kg rock in a horizontal circle on the end of a 1. 6 meter long string. If the velocity of the rock was 4 m/s, what is the Tension in the string? m = 0. 5 kg r = 1. 6 m v = 4 m/s The only centripetal force is Tension. T = m v 2 / r T = ½ 42 / 1. 6 T=5 N

WHEN CAN FORCES BE CENTRIPETAL FORCES? Gravity? Moon revolving around the Earth Tension? Twirling a pail at the end of a string Friction? Cars rounding a curve. Air Resistance? Birds flying in a circle. Normal? Riders in a carnival ride

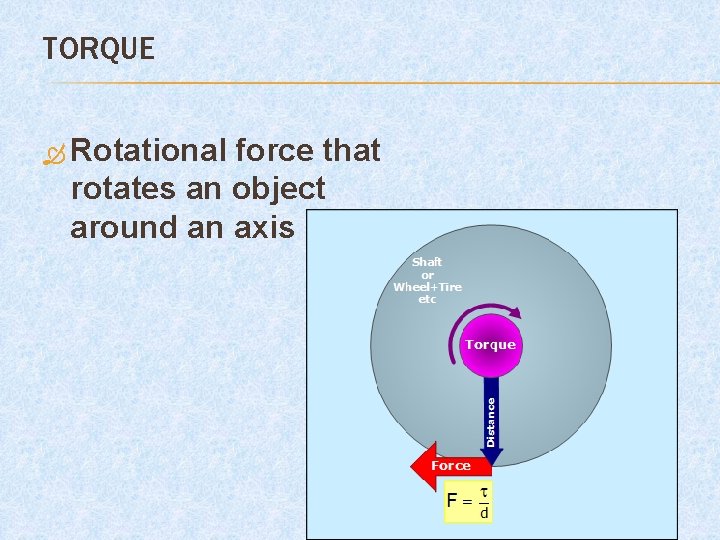
TORQUE Rotational force that rotates an object around an axis

Formula : τ= Force X radius Where radius is the length of the lever arm τ =Fr aka W= Fd Units are N • m aka “Newton meter”

LOOP THE LOOP What is the minimum speed that a rider must be moving at in order to complete a loop the loop of radius 12 m? The weight is the only centripetal force when the rider is moving at the minimum required speed. mg = mv 2/r g = v 2/r v 2 = rg v 2 = 12 x 10 v = 10. 95 m/s