Circular Motion AP Physics C Uniform Circular Motion

Circular Motion AP Physics C

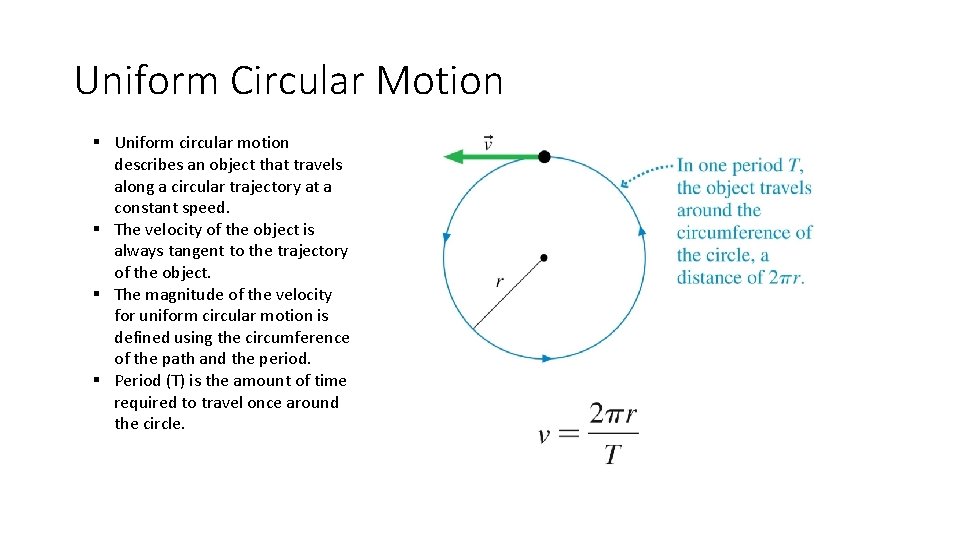
Uniform Circular Motion § Uniform circular motion describes an object that travels along a circular trajectory at a constant speed. § The velocity of the object is always tangent to the trajectory of the object. § The magnitude of the velocity for uniform circular motion is defined using the circumference of the path and the period. § Period (T) is the amount of time required to travel once around the circle.

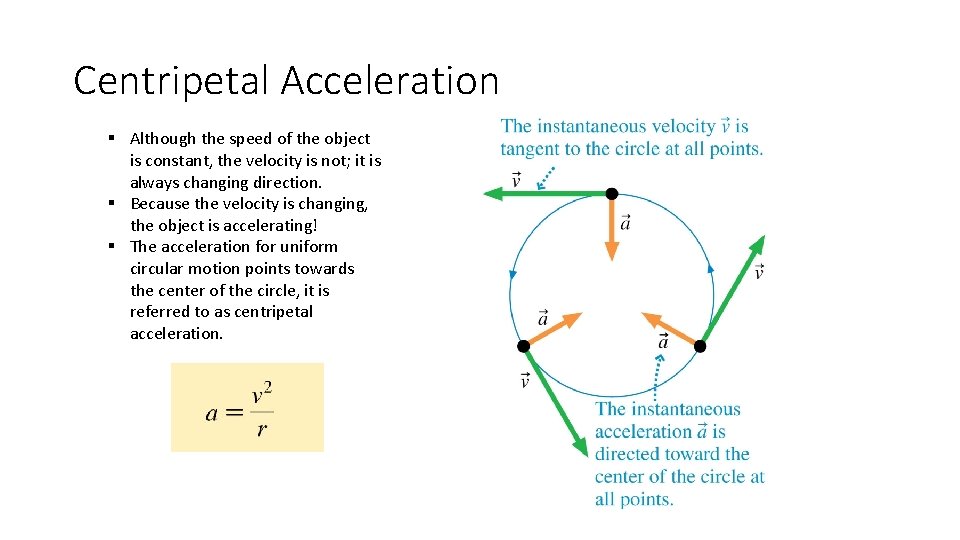
Centripetal Acceleration § Although the speed of the object is constant, the velocity is not; it is always changing direction. § Because the velocity is changing, the object is accelerating! § The acceleration for uniform circular motion points towards the center of the circle, it is referred to as centripetal acceleration.

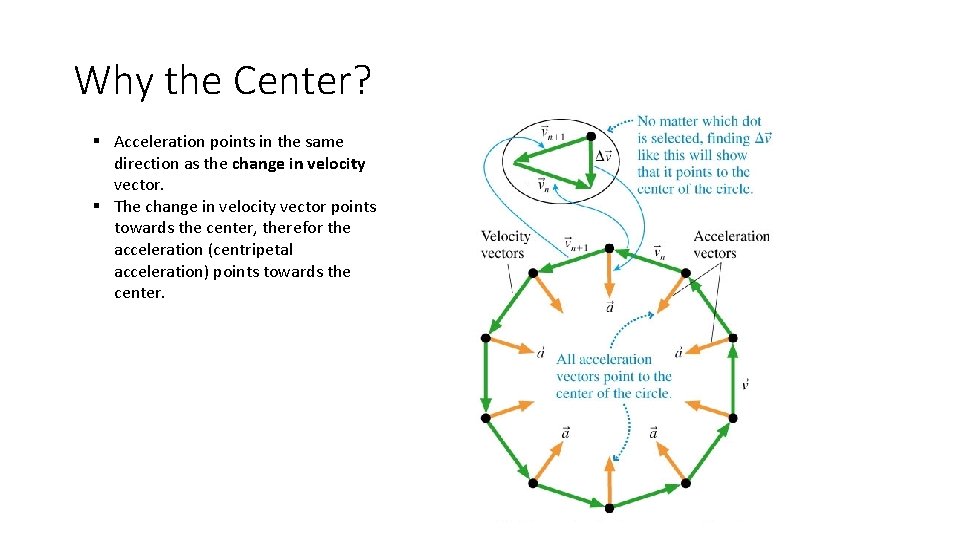
Why the Center? § Acceleration points in the same direction as the change in velocity vector. § The change in velocity vector points towards the center, therefor the acceleration (centripetal acceleration) points towards the center.

Centripetal Force § A particle of mass m moving at constant speed v around a circle of radius r must always have a net force of magnitude mv 2/r pointing toward the center of the circle. § This is not a new kind of force: The net force is due to one or more of our familiar forces such as tension, friction, or the normal force. § Centripetal force does not go on an FBD!

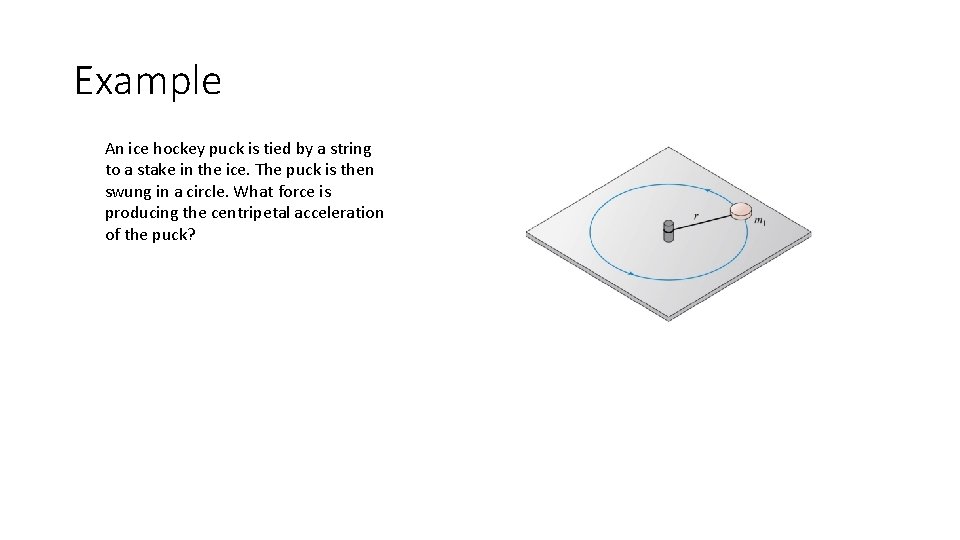
Example An ice hockey puck is tied by a string to a stake in the ice. The puck is then swung in a circle. What force is producing the centripetal acceleration of the puck?

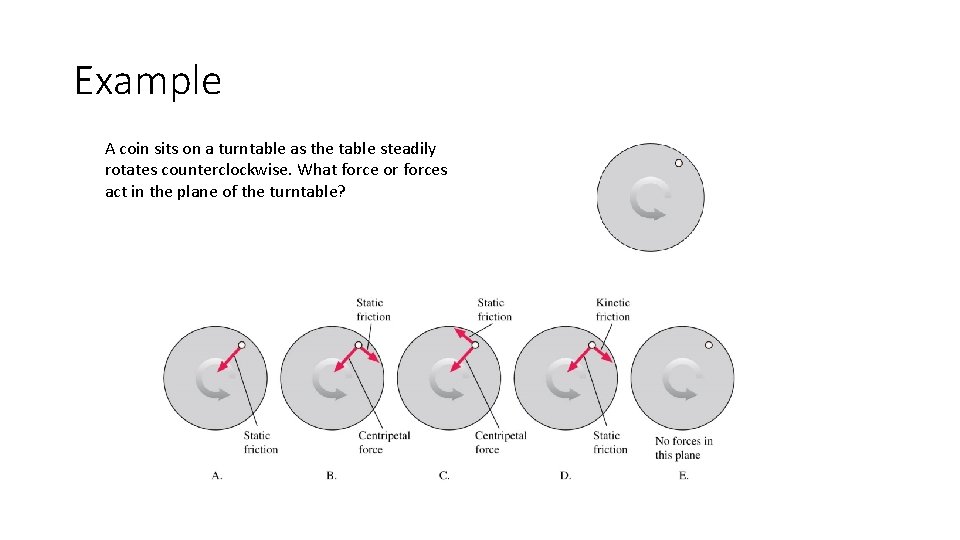
Example A coin sits on a turntable as the table steadily rotates counterclockwise. What force or forces act in the plane of the turntable?

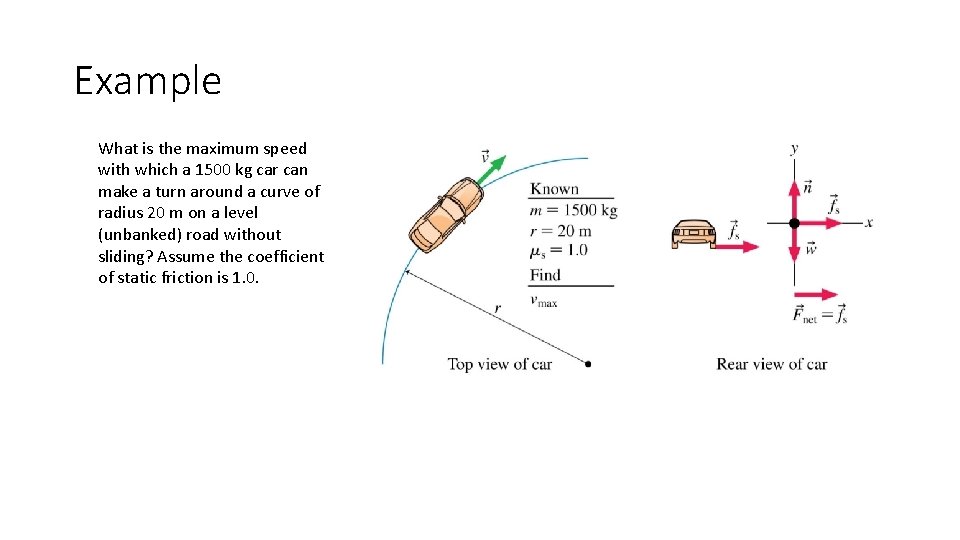
Example What is the maximum speed with which a 1500 kg car can make a turn around a curve of radius 20 m on a level (unbanked) road without sliding? Assume the coefficient of static friction is 1. 0.

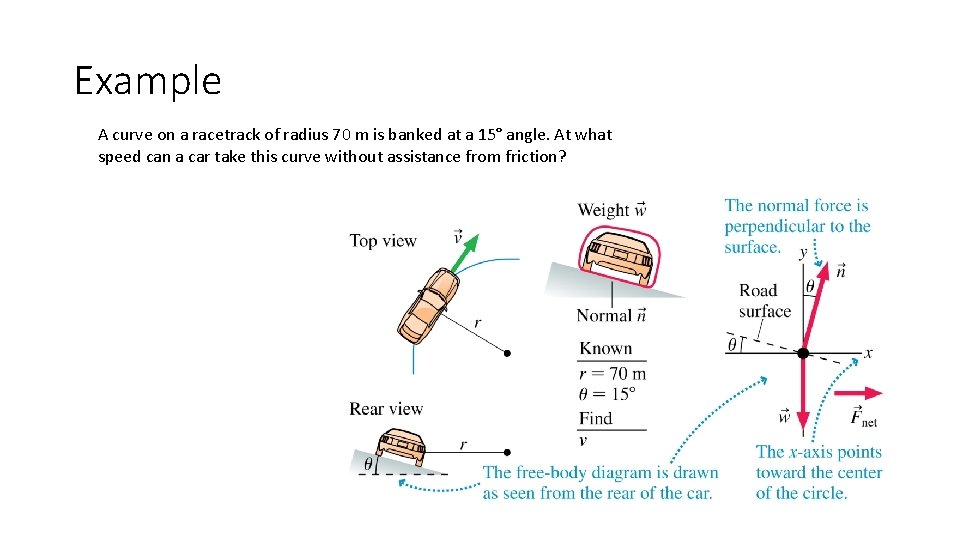
Example A curve on a racetrack of radius 70 m is banked at a 15° angle. At what speed can a car take this curve without assistance from friction?

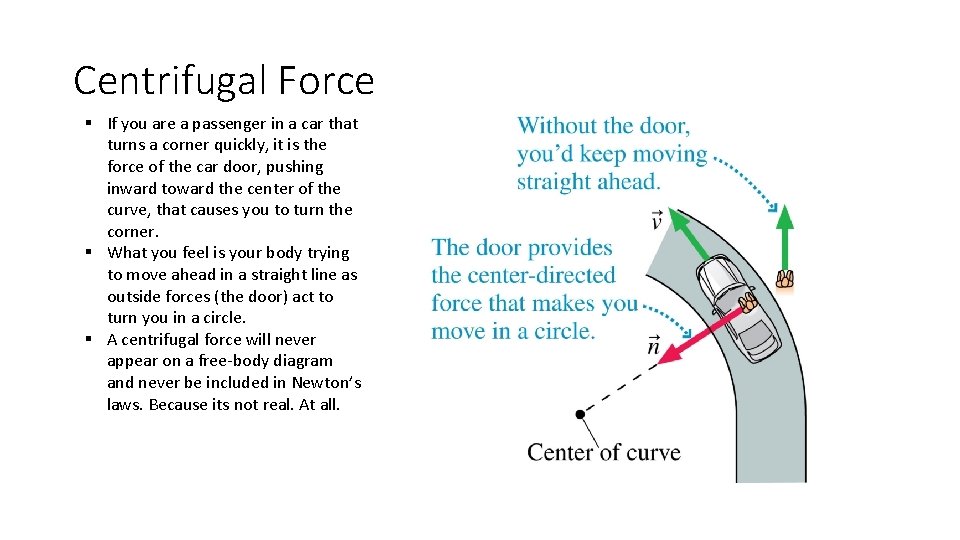
Centrifugal Force § If you are a passenger in a car that turns a corner quickly, it is the force of the car door, pushing inward toward the center of the curve, that causes you to turn the corner. § What you feel is your body trying to move ahead in a straight line as outside forces (the door) act to turn you in a circle. § A centrifugal force will never appear on a free-body diagram and never be included in Newton’s laws. Because its not real. At all.

The Gravitron § The Gravitron is a fun application of circular motion. This carnival ride spins fast enough that the riders appear to defy gravity. § As the ride speeds up, the normal force on the rider increases, which in turn increases the force of friction acting on the rider. § If this frictional force is large enough, it will perfectly cancel out the force of gravity!

Example An amusement park ride consists of a vertical cylinder that spins about a vertical axis. When the cylinder spins sufficiently fast, any person inside it is held up against the wall. Suppose that the coefficient of static friction between a typical person and the wall is 0. 25. Let the mass of an typical person be 60 kg, and let the radius of the cylinder be 7 m. Find the minimum speed the ride must have to prevent a person from falling to the bottom of the ride.

Non-Uniform Circular Motion § Acceleration can always be broken up into 2 components, parallel to velocity and perpendicular to velocity. § Parallel changes speed. § Perpendicular changes direction. § For uniform circular motion, the acceleration is only perpendicular, so no speed change. § For non-uniform, we have to deal with both components of acceleration.

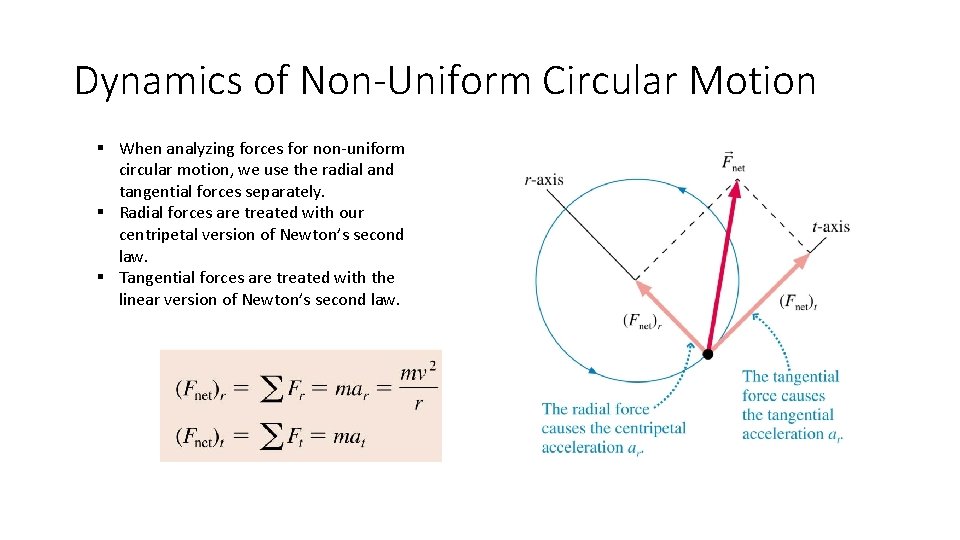
Dynamics of Non-Uniform Circular Motion § When analyzing forces for non-uniform circular motion, we use the radial and tangential forces separately. § Radial forces are treated with our centripetal version of Newton’s second law. § Tangential forces are treated with the linear version of Newton’s second law.

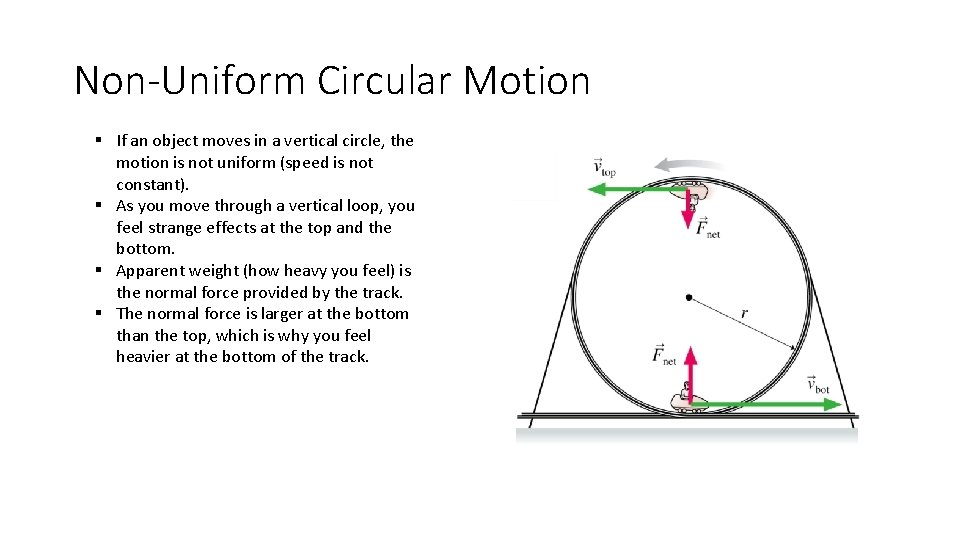
Non-Uniform Circular Motion § If an object moves in a vertical circle, the motion is not uniform (speed is not constant). § As you move through a vertical loop, you feel strange effects at the top and the bottom. § Apparent weight (how heavy you feel) is the normal force provided by the track. § The normal force is larger at the bottom than the top, which is why you feel heavier at the bottom of the track.

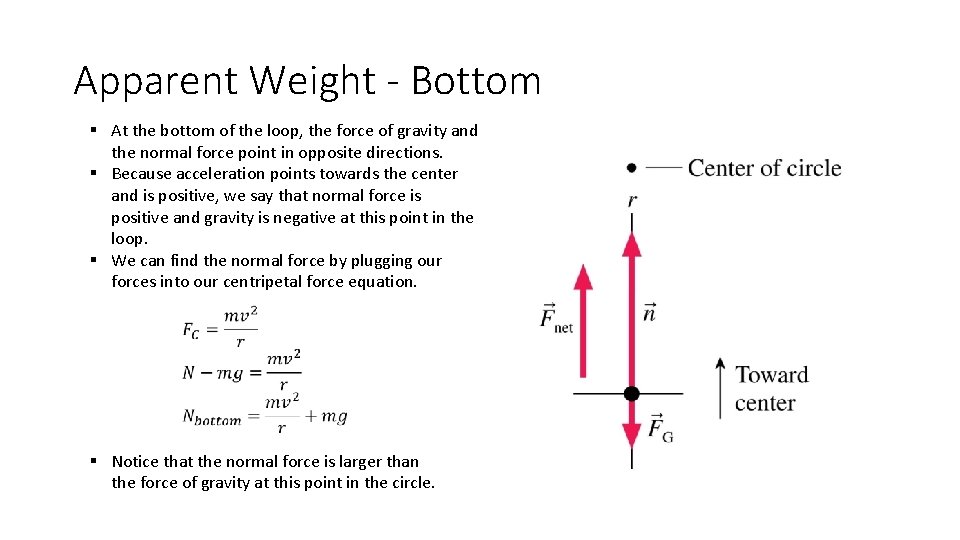
Apparent Weight - Bottom § At the bottom of the loop, the force of gravity and the normal force point in opposite directions. § Because acceleration points towards the center and is positive, we say that normal force is positive and gravity is negative at this point in the loop. § We can find the normal force by plugging our forces into our centripetal force equation. § Notice that the normal force is larger than the force of gravity at this point in the circle.

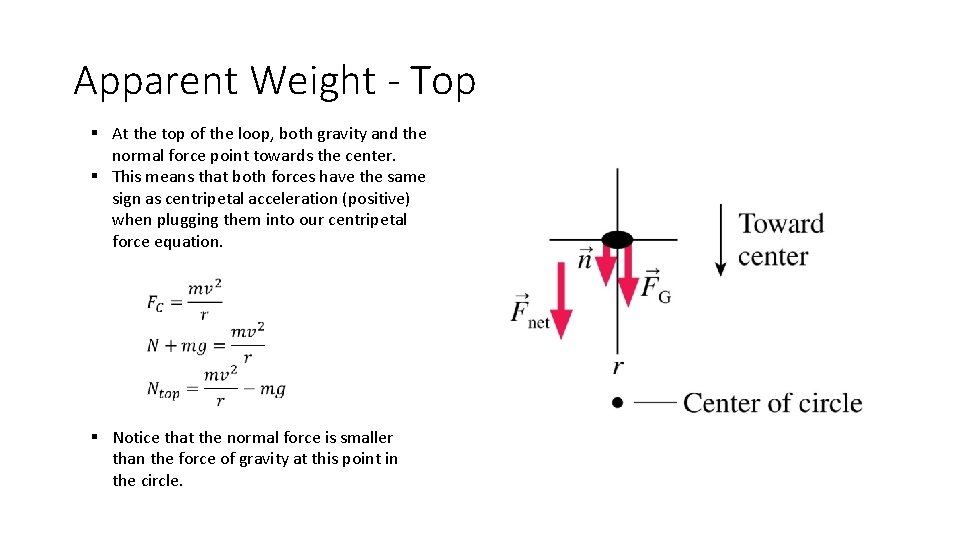
Apparent Weight - Top § At the top of the loop, both gravity and the normal force point towards the center. § This means that both forces have the same sign as centripetal acceleration (positive) when plugging them into our centripetal force equation. § Notice that the normal force is smaller than the force of gravity at this point in the circle.

Critical Speed § For an object moving in a vertical circle, there is a minimum speed it must have to not fall off the track. § This minimum speed occurs when the normal force is equal to 0. § If the normal force equals 0, the cart is no longer in contact with the track.

Example A handful of professional skaters have taken a skateboard through an inverted loop in a full pipe. For a typical pipe with a diameter 14 feet, what is the minimum speed the skater must have at the very top of the loop?

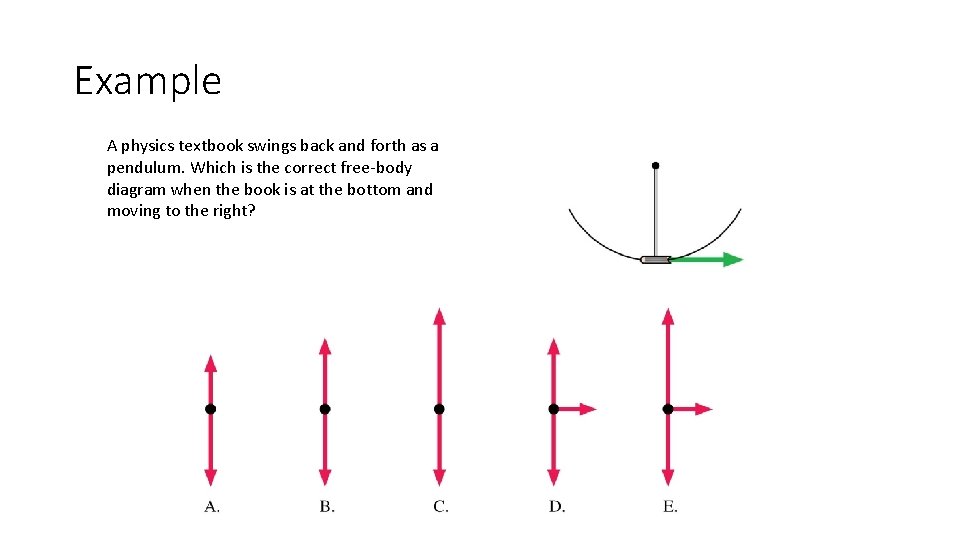
Example A physics textbook swings back and forth as a pendulum. Which is the correct free-body diagram when the book is at the bottom and moving to the right?

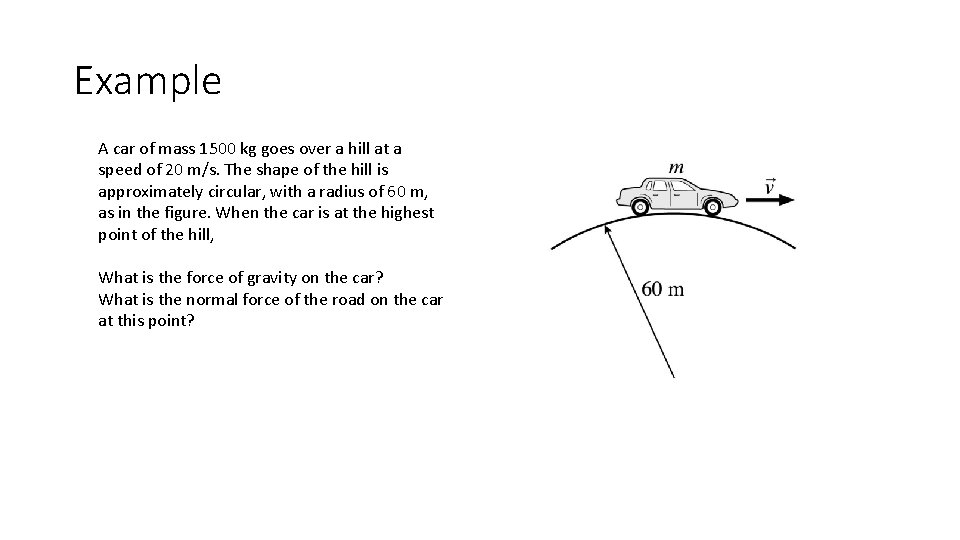
Example A car of mass 1500 kg goes over a hill at a speed of 20 m/s. The shape of the hill is approximately circular, with a radius of 60 m, as in the figure. When the car is at the highest point of the hill, What is the force of gravity on the car? What is the normal force of the road on the car at this point?

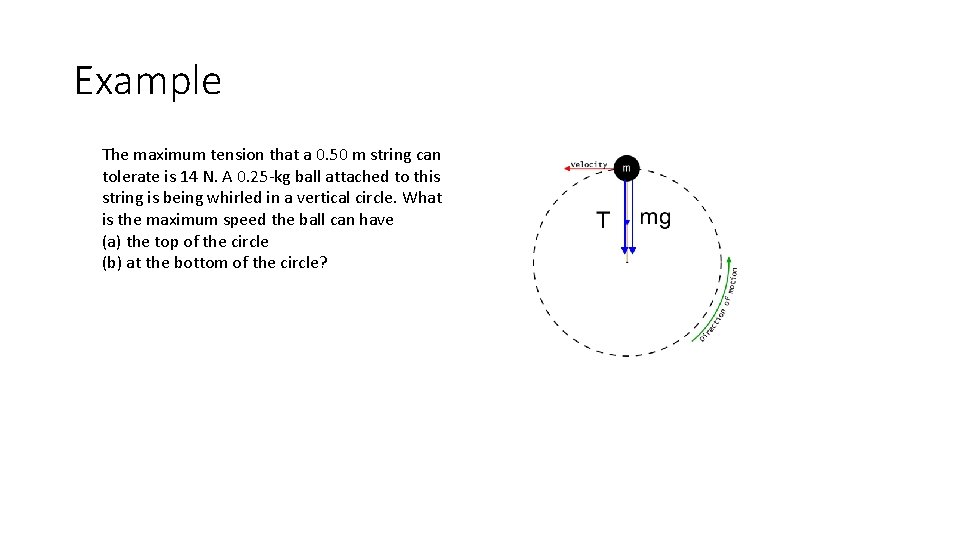
Example The maximum tension that a 0. 50 m string can tolerate is 14 N. A 0. 25 -kg ball attached to this string is being whirled in a vertical circle. What is the maximum speed the ball can have (a) the top of the circle (b) at the bottom of the circle?