CIRCULAR MOTION and GRAVITATION Chapter 5 Uniform Circular

CIRCULAR MOTION and GRAVITATION Chapter 5 – Uniform Circular Motion and Newton's Universal Law of Gravitation

Net Force causes Acceleration That means that a net force causes an object’s velocity to change… - To speed up - To slow down Net force in direction of motion (tangential) - To change direction or move in a curve Net force perpendicular to direction of motion (centripetal)

Uniform Circular Motion Magnitude of the velocity (speed) is constant, but the direction of the velocity continuously changes as object moves around in a circle v 0 r Dq v r The velocity vector at each instant, vt, is tangent to the path.

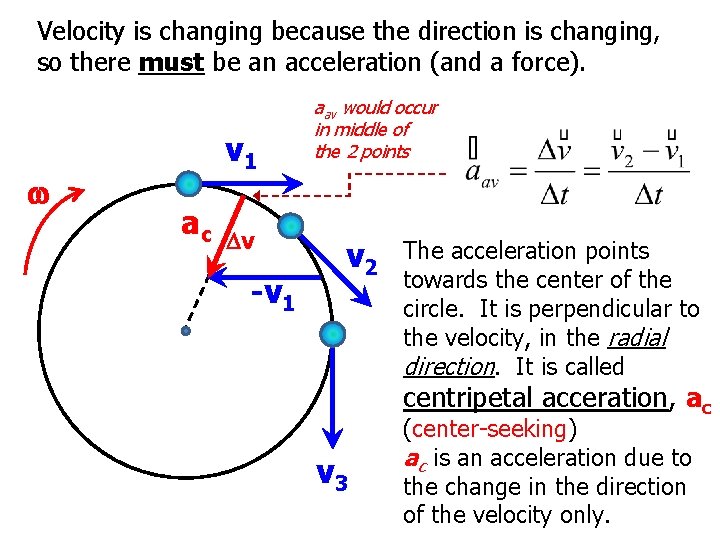
Velocity is changing because the direction is changing, so there must be an acceleration (and a force). w v 1 ac Dv -v 1 aav would occur in middle of the 2 points v 2 The acceleration points towards the center of the circle. It is perpendicular to the velocity, in the radial direction. It is called centripetal acceration, ac v 3 (center-seeking) ac is an acceleration due to the change in the direction of the velocity only.

Uniform Circular Motion Centripetal acceleration is the rate of change in velocity of an object when ONLY the DIRECTION of the velocity changes. It is always perpendicular to the velocity vector and points toward the center of the curve.

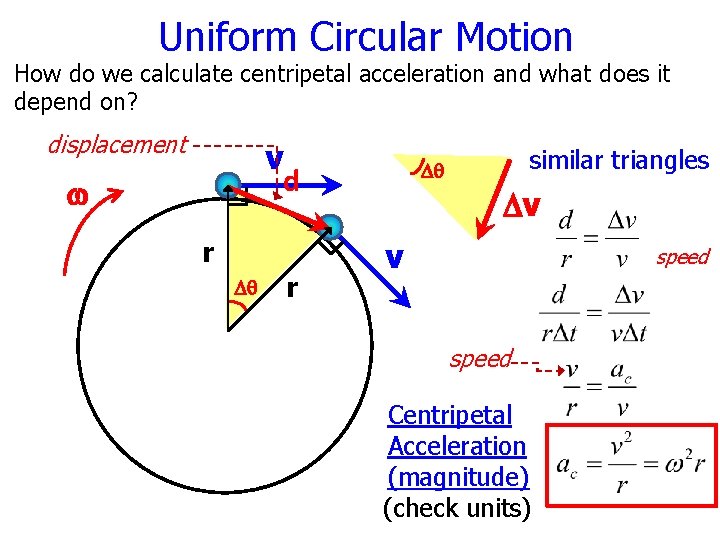
Uniform Circular Motion How do we calculate centripetal acceleration and what does it depend on? displacement v d w r Dq r similar triangles Dq Dv v speed Centripetal Acceleration (magnitude) (check units)

Special Cases of Acceleration An object traveling in a straight line at constant speed: An unsupported object near the surface of the earth: An object moving along a circular path:

Net Force causes Acceleration That means that a net force causes an object’s velocity to change… - To speed up - To slow down Net force in direction of motion (tangential) - To change direction only or move in a curve Net force perpendicular to direction of motion (centripetal)

Some terms for UCM: Period, T, time it takes to make 1 revolution (s) Frequency, f, number of revolutions in one second (s-1 or Hz) Tangential Speed, v, how many meters per sec v 0 r Dq v Angular speed, w, how many radians per sec

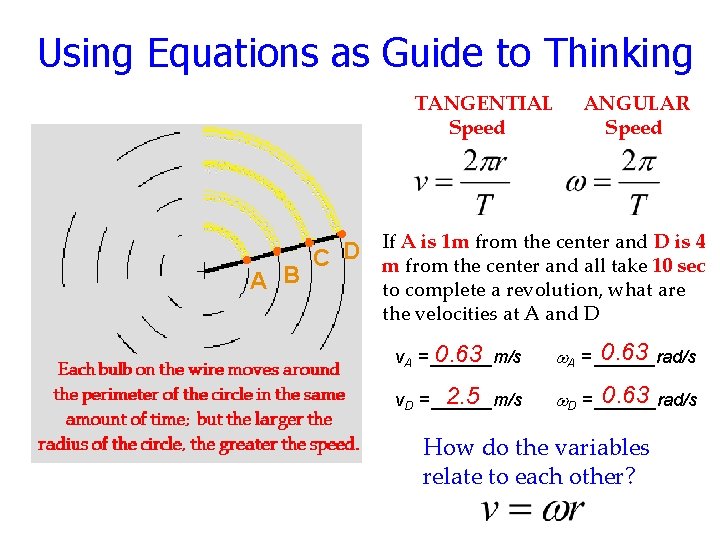
Using Equations as Guide to Thinking TANGENTIAL Speed ANGULAR Speed If A is 1 m from the center and D is 4 D C m from the center and all take 10 sec B A to complete a revolution, what are the velocities at A and D 0. 63 v. A = ______m/s 0. 63 w. A = ______rad/s 2. 5 v. D = ______m/s 0. 63 w. D = ______rad/s How do the variables relate to each other?

Example: Moon’s Centripetal Acceleration The moon’s nearly circular orbit about the Earth has a radius of about 384, 000 km and a period T of 27. 3 days. Determine the acceleration of the moon toward the Earth in m/s 2.

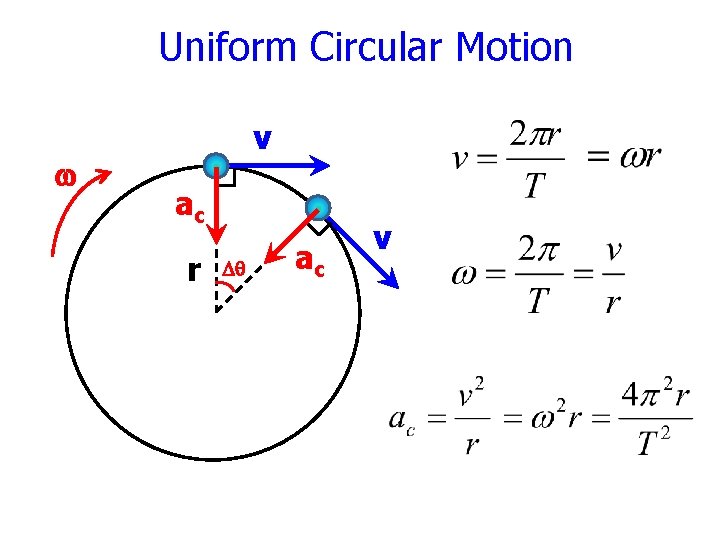
Uniform Circular Motion w v ac r Dq ac v

Uniform Circular Motion What causes centripetal acceleration? w v 1 ac r NET FORCE The net force is centripetal, in the direction of ac. Fc Dq v 2 Newtons 2 nd law: The centripetal force, FC, is perpendicular to the velocity (radial direction) and causes a change in the direction only. FC is found by adding all the forces in the radial direction

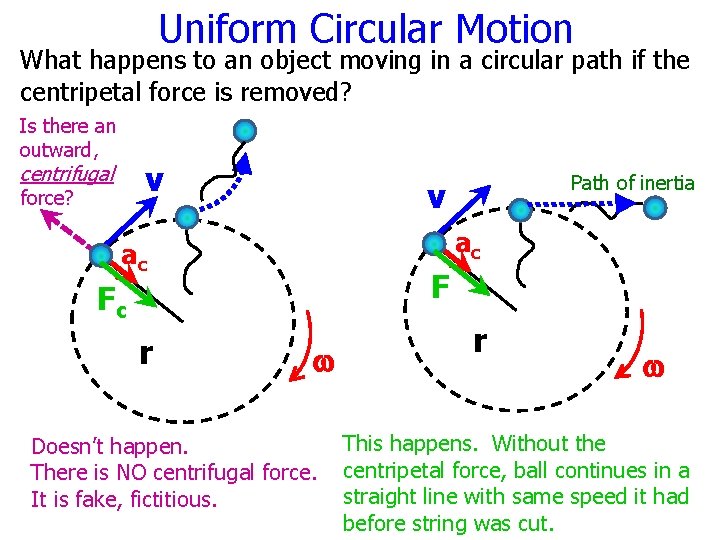
Uniform Circular Motion What happens to an object moving in a circular path if the centripetal force is removed? Is there an outward, v centrifugal force? v ac ac F Fc r Path of inertia w Doesn’t happen. There is NO centrifugal force. It is fake, fictitious. r w This happens. Without the centripetal force, ball continues in a straight line with same speed it had before string was cut.

Centripetal Force Inwardly directed resultant force which causes a body to turn; perpendicular to velocity. It is just a fancy name for the net force in the radial direction. Since it is a NET force, it is not drawn on a force diagram. Centripetal force always arises from the regular forces we are familiar with such as gravity, friction, tension, normal, electromagnetic. It is not a new kind of force. In our daily lives we come across many types of curved or circular motions. Centripetal force is necessary for any of these motions.

Car rounding a flat-curve

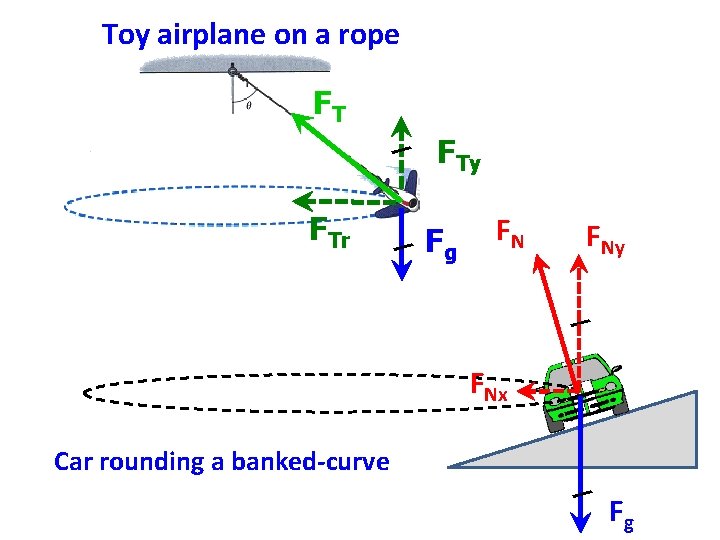
Toy airplane on a rope FT / / FTr FTy Fg FN FNy / FNx Car rounding a banked-curve / Fg

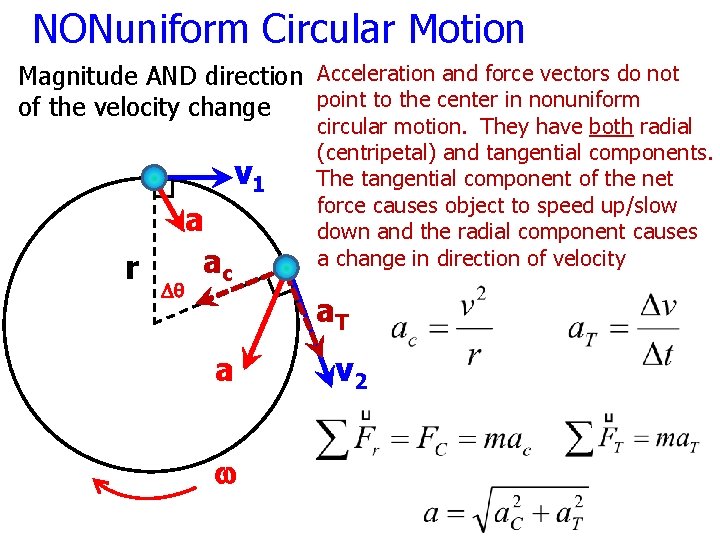
NONuniform Circular Motion Magnitude AND direction Acceleration and force vectors do not point to the center in nonuniform of the velocity change v 1 r Dq a ac circular motion. They have both radial (centripetal) and tangential components. The tangential component of the net force causes object to speed up/slow down and the radial component causes a change in direction of velocity a. T a w v 2

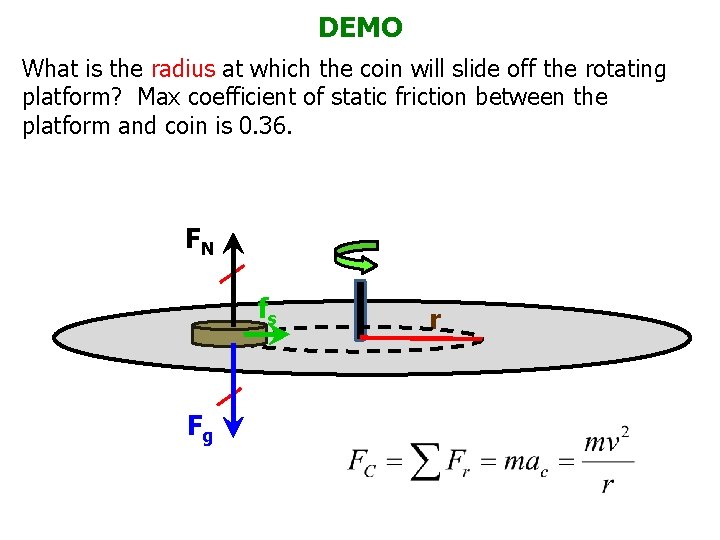
DEMO What is the radius at which the coin will slide off the rotating platform? Max coefficient of static friction between the platform and coin is 0. 36. FN fs Fg r

Example: Force on a revolving ball (horizontal) Estimate the force a person must exert on a string attached to a 0. 15 kg ball to make it revolve in a horizontal circle of radius 0. 600 m. The ball makes 2 revolutions per second. First: draw FBD and FT FG Very small, so neglect for now resolve forces into radial and non radial components Second: apply Newton's second law. Set net force in radial direction equal to mac.

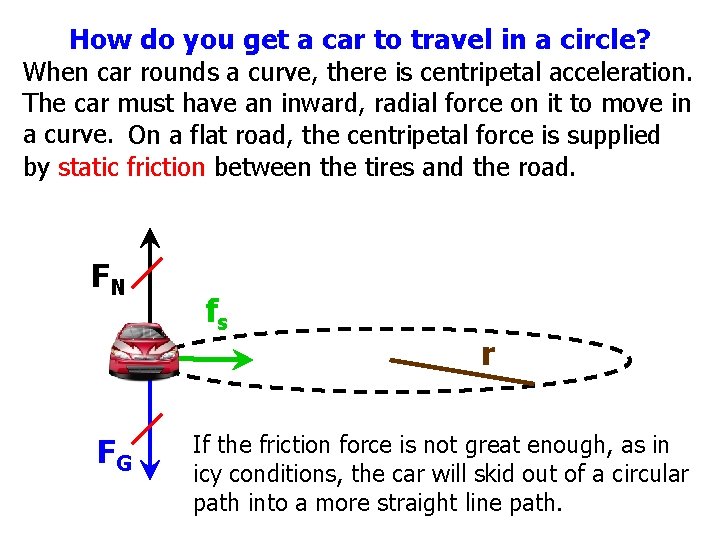
How do you get a car to travel in a circle? When car rounds a curve, there is centripetal acceleration. The car must have an inward, radial force on it to move in a curve. On a flat road, the centripetal force is supplied by static friction between the tires and the road. FN FG fs r If the friction force is not great enough, as in icy conditions, the car will skid out of a circular path into a more straight line path.

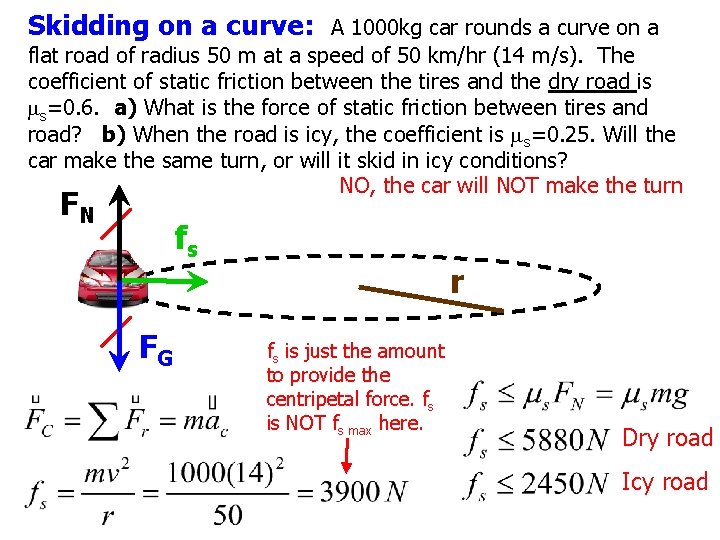
Skidding on a curve: A 1000 kg car rounds a curve on a flat road of radius 50 m at a speed of 50 km/hr (14 m/s). The coefficient of static friction between the tires and the dry road is ms=0. 6. a) What is the force of static friction between tires and road? b) When the road is icy, the coefficient is ms=0. 25. Will the car make the same turn, or will it skid in icy conditions? NO, the car will NOT make the turn FN fs FG r fs is just the amount to provide the centripetal force. fs is NOT fs max here. Dry road Icy road

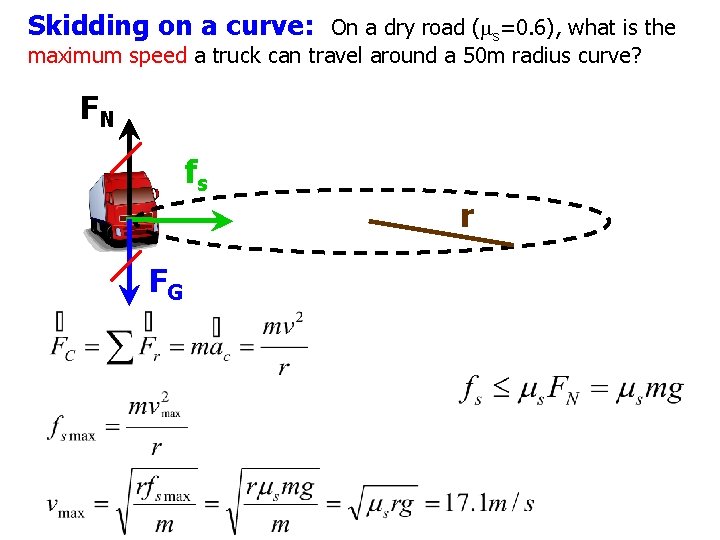
Skidding on a curve: On a dry road (ms=0. 6), what is the maximum speed a truck can travel around a 50 m radius curve? FN fs FG r

Approach for Analyzing the Circular Dynamics 1. Draw a picture. Position the object at a place in the circle where all the forces acting on it can be visualized and drawn. 2. Select a coordinate system to analyze your system with one axis in the radial direction (along the direction of acceleration) and the other perpendicular to the radial direction (nonradial). 3. Identify all forces acting on the system by drawing a free body diagram. Your FBD should be large and clear 4. Resolve force vectors into radial and non-radial (perpendicular) components. 5. Apply Newton’s 2 nd law to each axis or direction: Fc = SFr = mac = mv 2/r and FNR = SFx or y = max or y Force and acceleration directions for radial axis: is pointing INTO the circle, is OUT of circle + 6. Solve for relevant unknowns. -

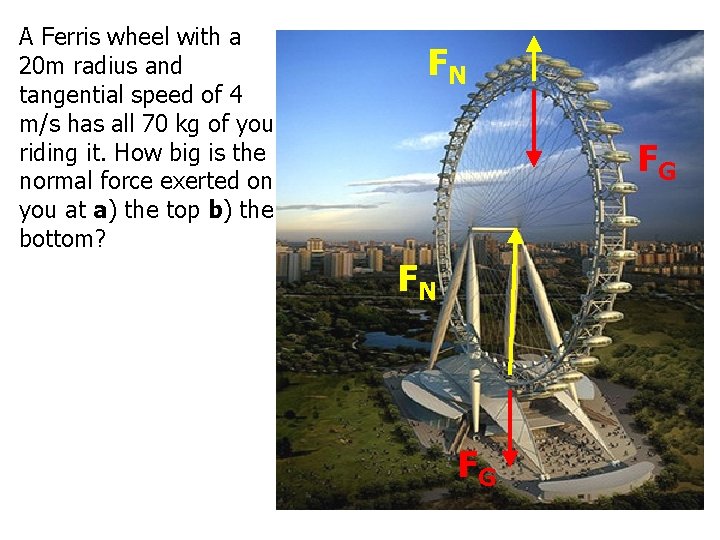
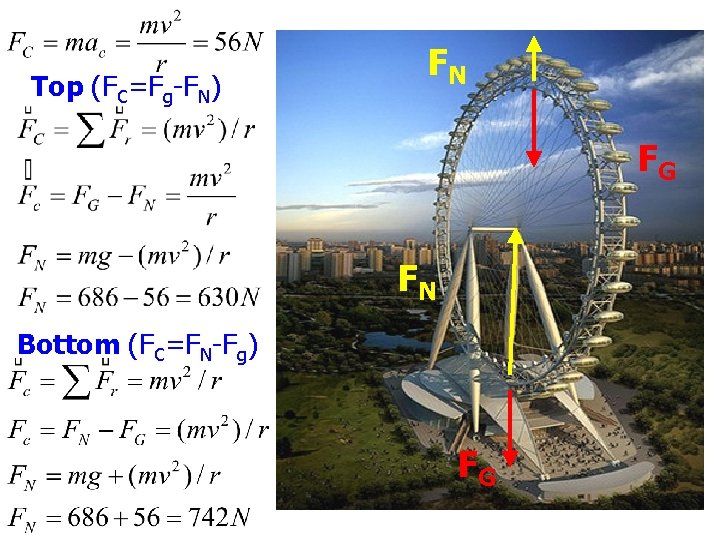
A Ferris wheel with a 20 m radius and tangential speed of 4 m/s has all 70 kg of you riding it. How big is the normal force exerted on you at a) the top b) the bottom? FN FG

Top (FC=Fg-FN) FN FG FN Bottom (FC=FN-Fg) FG

What is the MAX speed the Ferris wheel can go? Top (FC=Fg-FN) At max speed, FN=0 FG FN Bottom (FC=FN-Fg) At top and bottom FG

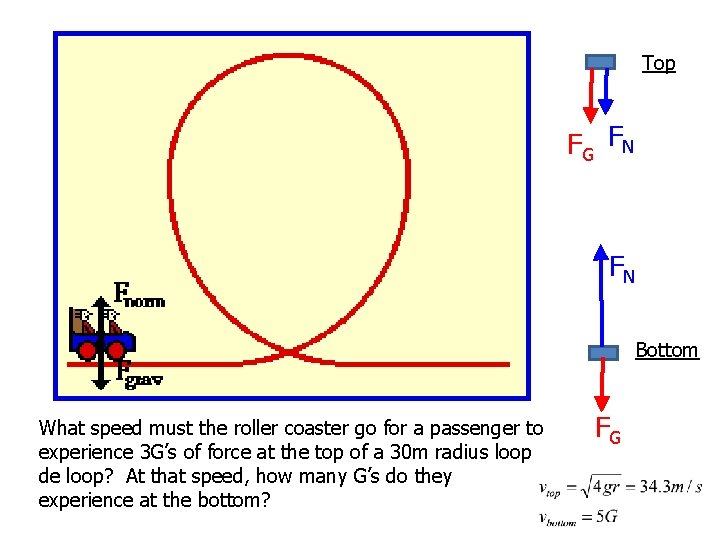
Top FG FN FN Bottom What speed must the roller coaster go for a passenger to experience 3 G’s of force at the top of a 30 m radius loop de loop? At that speed, how many G’s do they experience at the bottom? FG

Conical Pendulum: Tetherball. The game of tetherball is played with a ball tied to a pole with a string. When the ball is struck, it whirls around the pole. In what direction is the acceleration of the ball and what force causes the acceleration? Draw a FBD of the ball and resolve forces into radial and non radial components The net force points horizontally toward the center of rotation. The horizontal-component of the tension force is the centripetal force and it causes centripetal acceleration. y FT FTx FG x

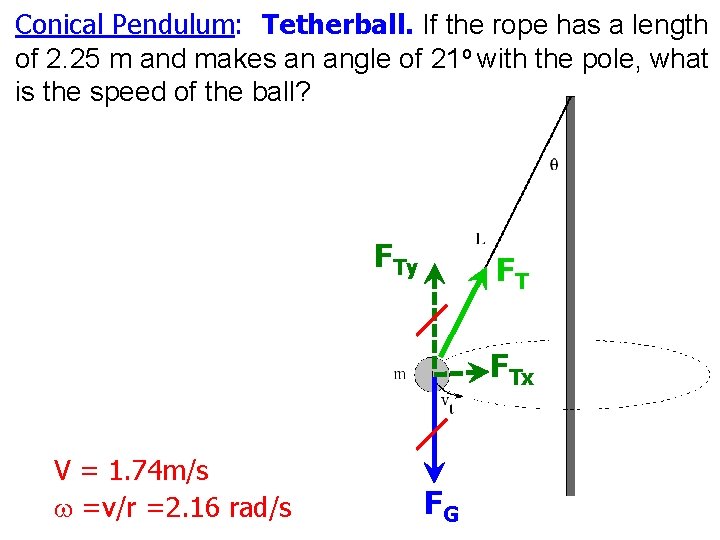
Conical Pendulum: Tetherball. If the rope has a length of 2. 25 m and makes an angle of 21 o with the pole, what is the speed of the ball? FTy FT FTx V = 1. 74 m/s w =v/r =2. 16 rad/s FG

For banked turns cars and motorcycles on wall of death globe of death wall of death

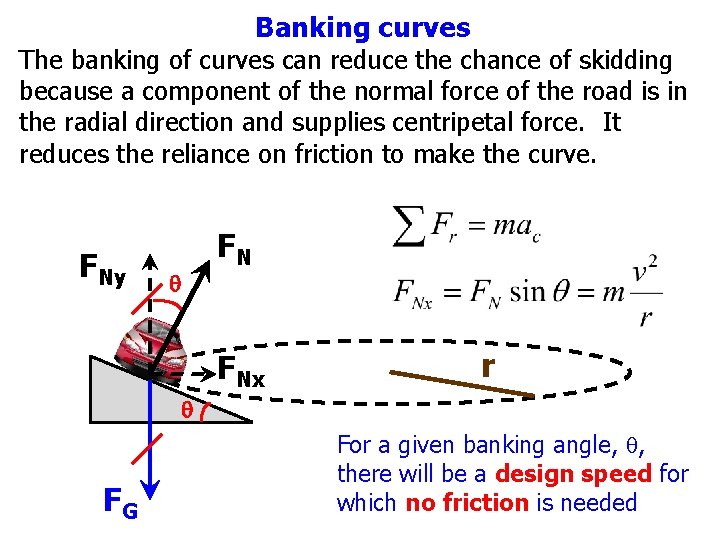
Banking curves The banking of curves can reduce the chance of skidding because a component of the normal force of the road is in the radial direction and supplies centripetal force. It reduces the reliance on friction to make the curve. FNy q FN FNx r q FG For a given banking angle, q, there will be a design speed for which no friction is needed

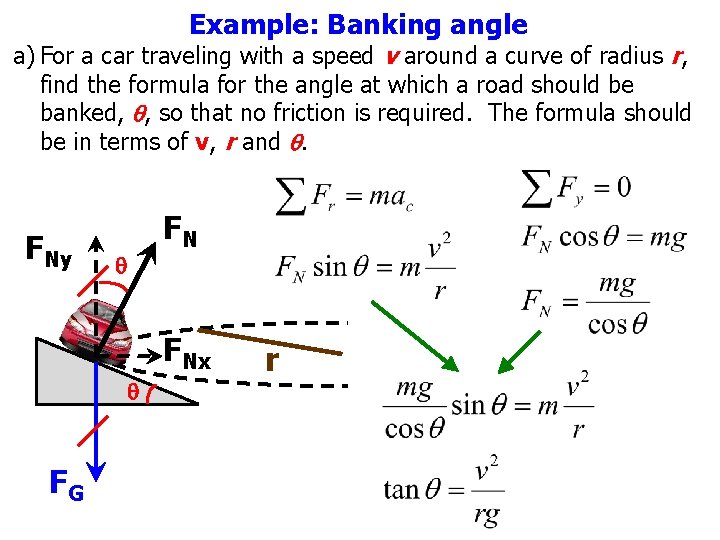
Example: Banking angle a) For a car traveling with a speed v around a curve of radius r, find the formula for the angle at which a road should be banked, q, so that no friction is required. The formula should be in terms of v, r and q. FNy q FN FNx q FG r

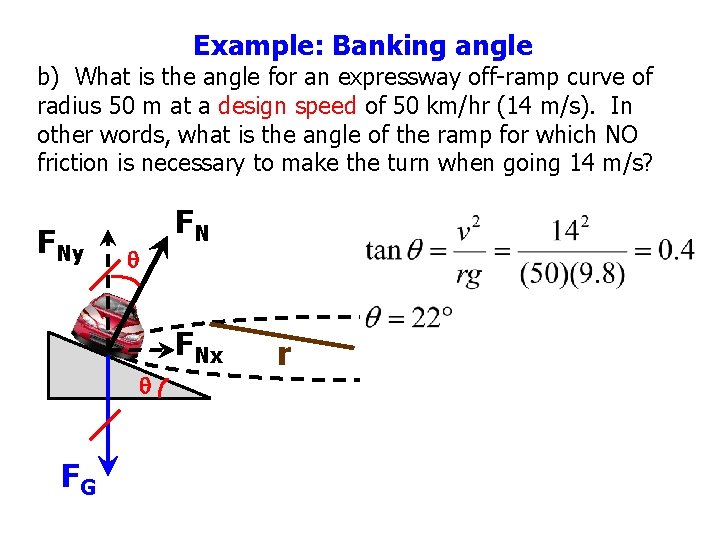
Example: Banking angle b) What is the angle for an expressway off-ramp curve of radius 50 m at a design speed of 50 km/hr (14 m/s). In other words, what is the angle of the ramp for which NO friction is necessary to make the turn when going 14 m/s? FNy q FN FNx q FG r

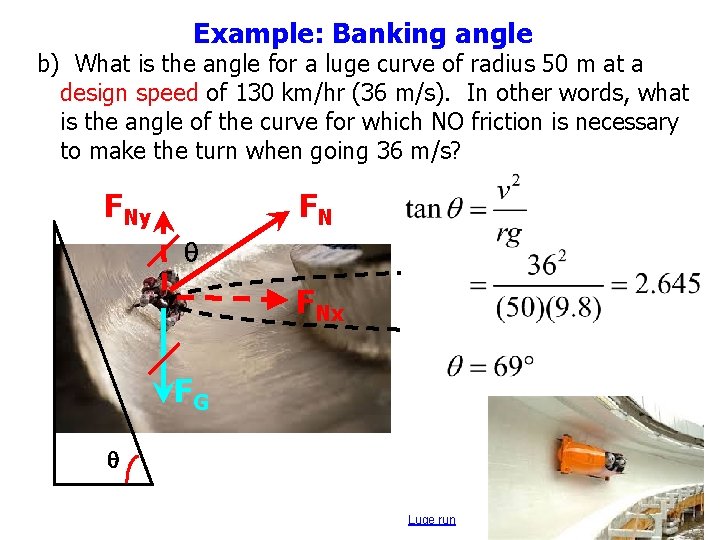
Example: Banking angle b) What is the angle for a luge curve of radius 50 m at a design speed of 130 km/hr (36 m/s). In other words, what is the angle of the curve for which NO friction is necessary to make the turn when going 36 m/s? FN FNy q FNx FG q Luge run

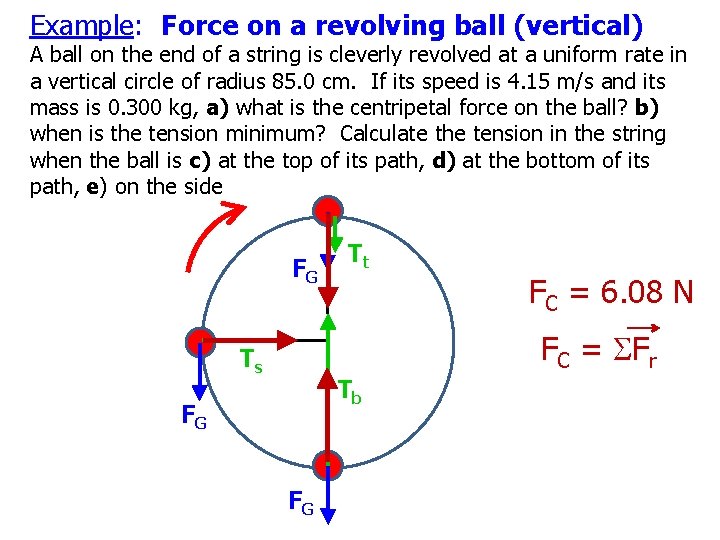
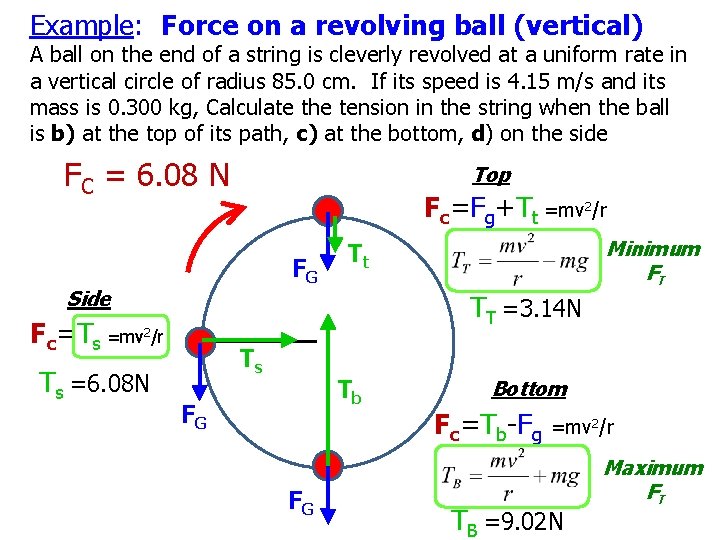
Example: Force on a revolving ball (vertical) A ball on the end of a string is cleverly revolved at a uniform rate in a vertical circle of radius 85. 0 cm. If its speed is 4. 15 m/s and its mass is 0. 300 kg, a) what is the centripetal force on the ball? b) when is the tension minimum? Calculate the tension in the string when the ball is c) at the top of its path, d) at the bottom of its path, e) on the side FG Tt FC = 6. 08 N FC = SFr Ts Tb FG FG

Example: Force on a revolving ball (vertical) A ball on the end of a string is cleverly revolved at a uniform rate in a vertical circle of radius 85. 0 cm. If its speed is 4. 15 m/s and its mass is 0. 300 kg, Calculate the tension in the string when the ball is b) at the top of its path, c) at the bottom, d) on the side FC = 6. 08 N Top Fc=Fg+Tt =mv 2/r FG Side TT =3. 14 N Fc=Ts =mv 2/r Ts =6. 08 N Minimum FT Tt Ts Tb FG FG Bottom Fc=Tb-Fg =mv 2/r TB =9. 02 N Maximum FT

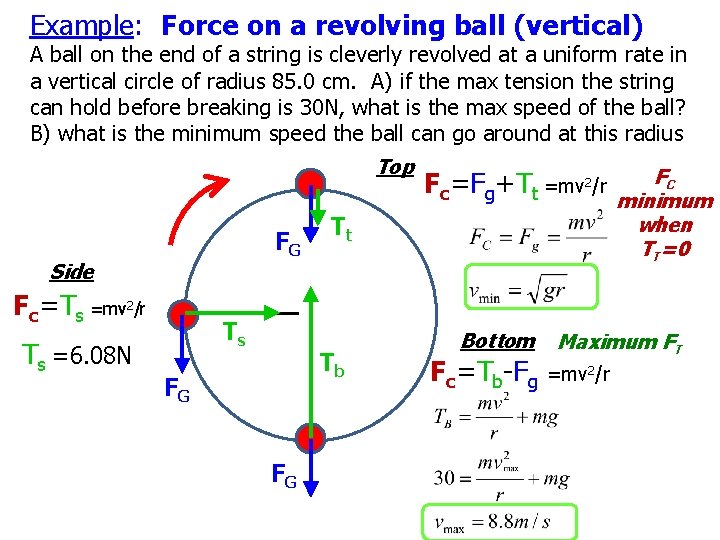
Example: Force on a revolving ball (vertical) A ball on the end of a string is cleverly revolved at a uniform rate in a vertical circle of radius 85. 0 cm. A) if the max tension the string can hold before breaking is 30 N, what is the max speed of the ball? B) what is the minimum speed the ball can go around at this radius Top F Fc=Fg+Tt =mv 2/r FG Side Fc=Ts =mv 2/r Ts =6. 08 N Ts Tt Tb FG FG Bottom Fc=Tb-Fg C minimum when TT=0 Maximum FT =mv 2/r

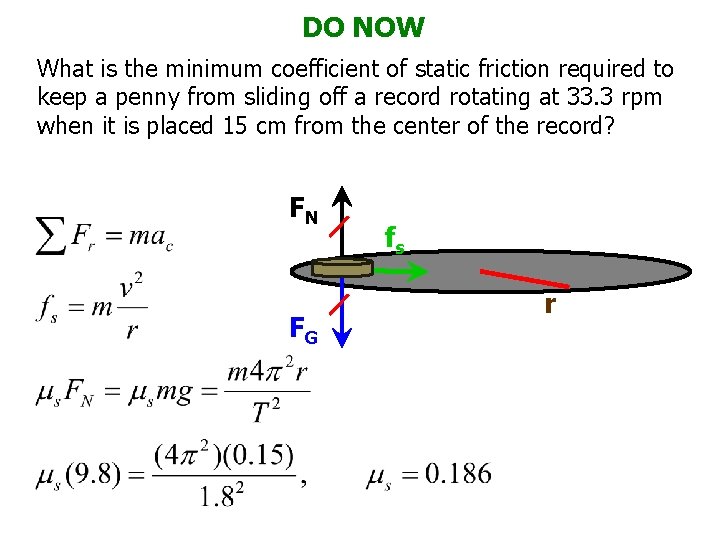
DO NOW What is the minimum coefficient of static friction required to keep a penny from sliding off a record rotating at 33. 3 rpm when it is placed 15 cm from the center of the record? FN FG fs r

Example: Ultracentrifuge An ultracentrifuge rotor rotates at 50, 000 rpm. The bottom of a 4. 00 cm long test tube is 10. 0 cm from the rotation axis. Calculate the centripetal acceleration in “g’s” at the bottom of the tube. If the contents of the tube have a total mass of 12. 0 g, what force must the bottom of the tube withstand? (Equivalent to about 3. 3 tons)

The Earth spins on its axis and we move with it in circular motion around the center. (The radius of the Earth at the equator is RE = 6. 38 x 106 m ) a) What is the centripetal acceleration at the equator? b) What is the centripetal force acting on a 55 kg person standing at the equator preventing that person from drifting off tangentially into space? c) What provides that required centripetal force to keep us on the earth as is rotates? m = 55 kg FN FG (your scale reads 0. 34% less than your true weight at the equator)

DO NOW d) How fast does the Earth have to spin to make us “weightless” at the equator (find the period)? m = 55 kg FG (you would drift off the equator if the earth day was <84. 5 min)

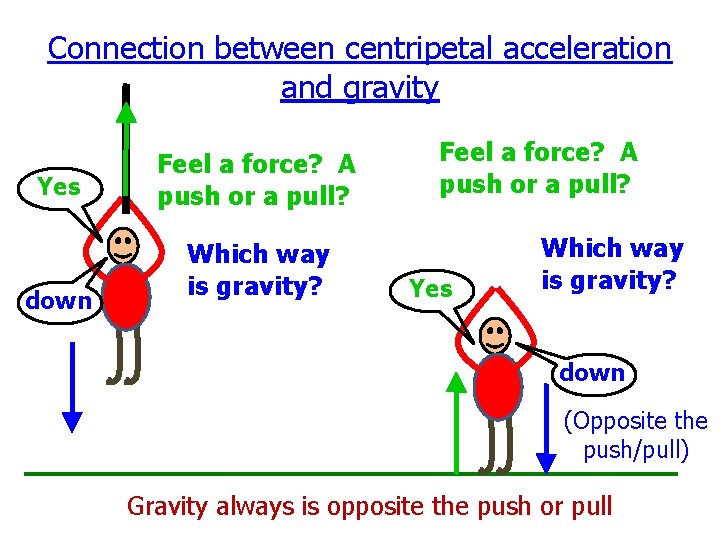
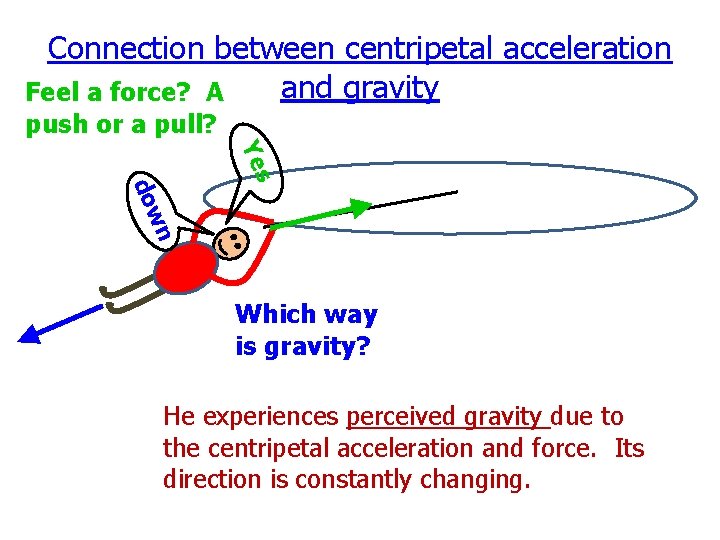
Connection between centripetal acceleration and gravity Yes down Feel a force? A push or a pull? Which way is gravity? Feel a force? A push or a pull? Yes Which way is gravity? down (Opposite the push/pull) Gravity always is opposite the push or pull

Connection between centripetal acceleration and gravity Feel a force? A push or a pull? s Ye wn do Which way is gravity? He experiences perceived gravity due to the centripetal acceleration and force. Its direction is constantly changing.

Connection between centripetal acceleration and gravity Space station in outer space where there is no gravity. Can create gravity with centripetal force. w Feel a force? A push or a pull? Yes Which way is gravity? down http: //www. youtube. com/watch? v=sk 0 Zah. SHKs. Q

Connection between centripetal acceleration and gravity How fast do we need to rotate the space station to mimic gravity? Lets say the space station has 500 m radius. w FN=mac If ac = g, then FN = mg and artificial gravity can be created by rotating the station. What v and T should the station go to simulate Earth gravity? What about the center?

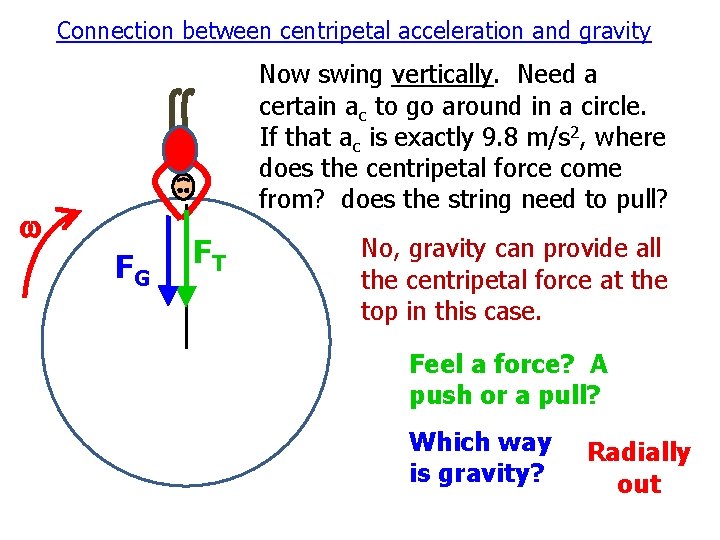
Connection between centripetal acceleration and gravity Now swing vertically. Need a certain ac to go around in a circle. If that ac is exactly 9. 8 m/s 2, where does the centripetal force come from? does the string need to pull? w FG FT No, gravity can provide all the centripetal force at the top in this case. Feel a force? A push or a pull? Which way is gravity? Radially out

Newton’s Universal Law of Gravitation

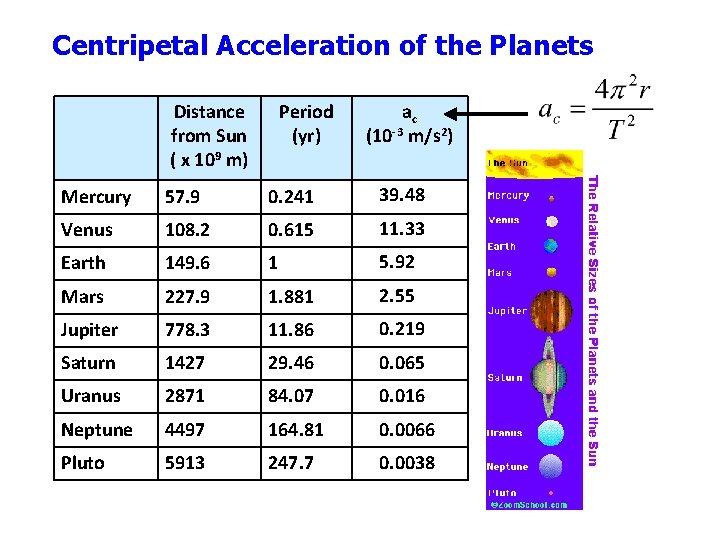
Centripetal Acceleration of the Planets Distance from Sun ( x 109 m) Period (yr) ac (10 -3 m/s 2) Mercury 57. 9 0. 241 39. 48 Venus 108. 2 0. 615 11. 33 Earth 149. 6 1 5. 92 Mars 227. 9 1. 881 2. 55 Jupiter 778. 3 11. 86 0. 219 Saturn 1427 29. 46 0. 065 Uranus 2871 84. 07 0. 016 Neptune 4497 164. 81 0. 0066 Pluto 5913 247. 7 0. 0038

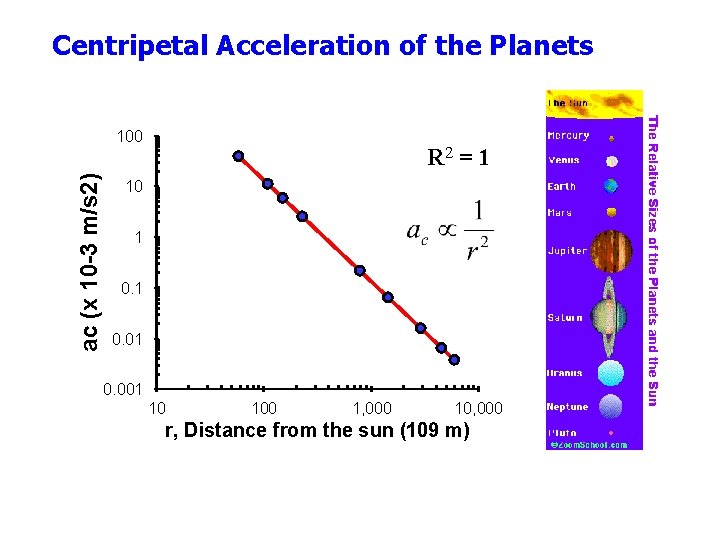
Centripetal Acceleration of the Planets ac (x 10 -3 m/s 2) 100 R 2 = 1 10 1 0. 01 0. 001 10 100 1, 000 10, 000 r, Distance from the sun (109 m)

Newton’s Universal Law of Gravitation r m 1 Inverse Square Law (G = 6. 6742 x 10 -11 N m 2/kg 2) m 2

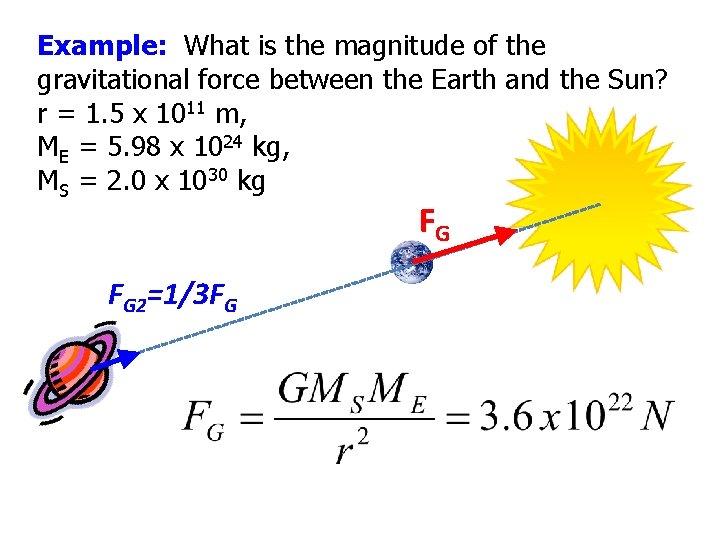
Example: What is the magnitude of the gravitational force between the Earth and the Sun? r = 1. 5 x 1011 m, ME = 5. 98 x 1024 kg, MS = 2. 0 x 1030 kg FG FG 2=1/3 FG

Example: Spacecraft at 2 r. E. On the surface of the earth, a spacecraft weighs 20, 000 N. What is the spacecraft’s weight (force of gravity acting on it) when it orbits 2 earth radii from the earth’s center

Gravitational Field Strength above the surface Consider an object of mass m, at or near the surface of the earth (a distance r=RE from the Earth’s center), for example an apple. It is pulled by the force of gravity. According to Newton’s 2 nd law, the apple experiences an acceleration mg due to the net force FG (in the absence of other forces). r RE r. E = 6. 36 x 106 m m m At Earths Surface, r=RE g = 9. 8 N/kg Gravitational field strength, g, decreases with r 2. In this example, the field is created by the Earth.

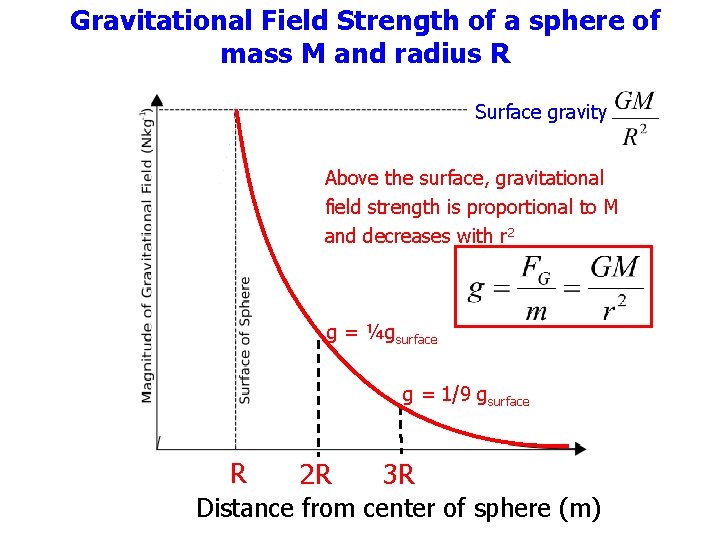
Gravitational Field Strength of a sphere of mass M and radius R Surface gravity Above the surface, gravitational field strength is proportional to M and decreases with r 2 g = ¼gsurface g = 1/9 gsurface R 2 R 3 R Distance from center of sphere (m)

Gravitational Field Strength can also be expressed in terms of density instead of mass Determine the density of the Earth. (The radius of the Earth is 6. 36 x 106 m) Gravitational Field strength around an object of mass M r At Earth’s surface, r=RE and g= 9. 8 N/m Surface gravity can be expressed in terms of density

Gravitational Field Find the surface gravitational field strength, g. J, of Jupiter’s mass is 317. 8 times that of the Earth and its radius is about 11 times bigger than the Earths’. Gravitational field strength value of g on other planets

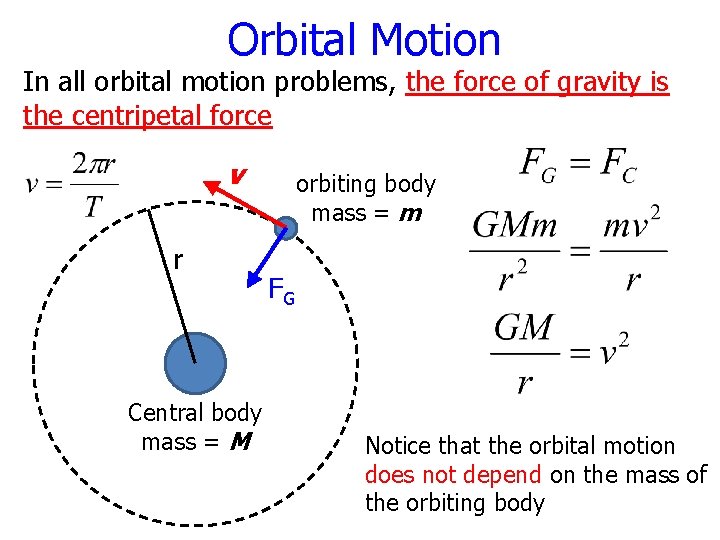
Orbital Motion In all orbital motion problems, the force of gravity is the centripetal force v r Central body mass = M orbiting body mass = m FG Notice that the orbital motion does not depend on the mass of the orbiting body

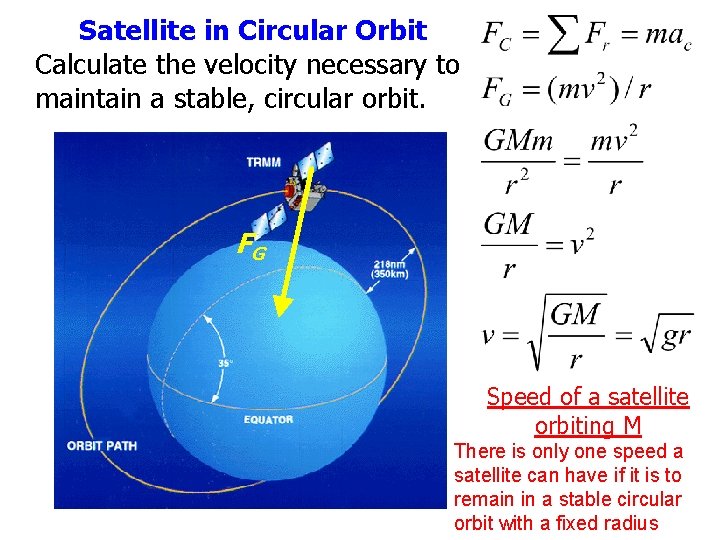
Satellite in Circular Orbit Calculate the velocity necessary to maintain a stable, circular orbit. FG Speed of a satellite orbiting M There is only one speed a satellite can have if it is to remain in a stable circular orbit with a fixed radius

Geosynchronous satellite. A geosynchronous satellite is one that stays above the same point on the equator of the Earth. Such satellites are used for cable TV transmission, weather forecasting and communication relays. For a geosynchronous sat, determine a) the height above the Earth’s surface b) orbital speed T = 1 day = 86, 400 s Orbital Radius = Distance from Earth’s center: r = 4. 23 x 107 m Height of satellite above Earth: v = 2 pr/T h = r – r. E = 36, 000 km (6 r. E)

Example: Geosynchronous satellite. b) satellite’s speed. Distance of satellite from Earth’s center: r = 4. 23 x 107 m v = 3070 m/s (6900 mph)

Example: The Sun’s Mass. Determine the mass of the Sun given the Earth’s distance from the Sun is r. ES=1. 5 x 1011 m. FG r v = 2 pr/T (T E= 1 yr = 3. 16 x 107 s)

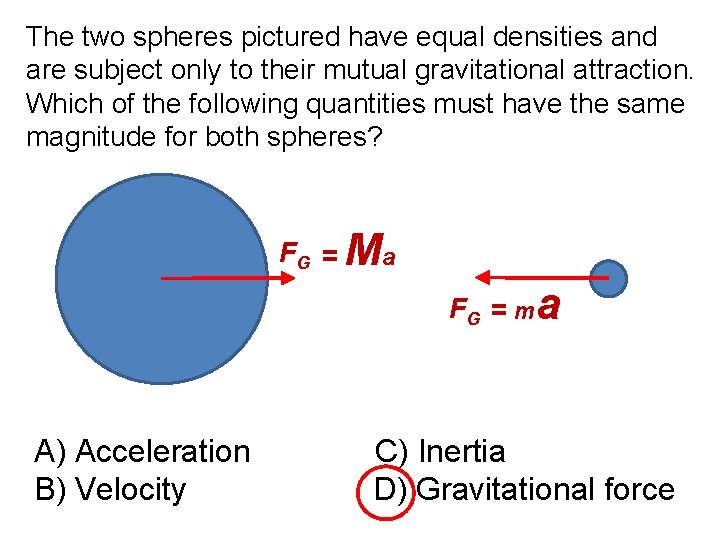
The two spheres pictured have equal densities and are subject only to their mutual gravitational attraction. Which of the following quantities must have the same magnitude for both spheres? F G = Ma F G = ma A) Acceleration C) Inertia B) Velocity D) Gravitational force

Gravity holds many objects together in orbits. Moons…

… more moons, planets …. satellites…

… and astronauts and their space shuttles. But wait…

Why do astronauts in orbit seem to float? Have they escaped the Earth’s gravity?

Example: Gravity in orbit. Calculate the force of gravity on a 50 kg astronaut standing on Earth. Then calculate the force of gravity on the astronaut in orbit. The shuttle orbits the Earth at an orbital radius of about 6. 68 x 106 m. r=6. 68 x 106 m ME=5. 98 x 1024 kg G=6. 67 x 10 -11 N m 2/kg 2 Astronaut in Room S 17 Astronaut in orbit: FG =mg= 490 N FG = 447 N

According to your results, does the floating make sense? Do the astronauts feel a significantly different force of gravity when in orbit? What’s going on?

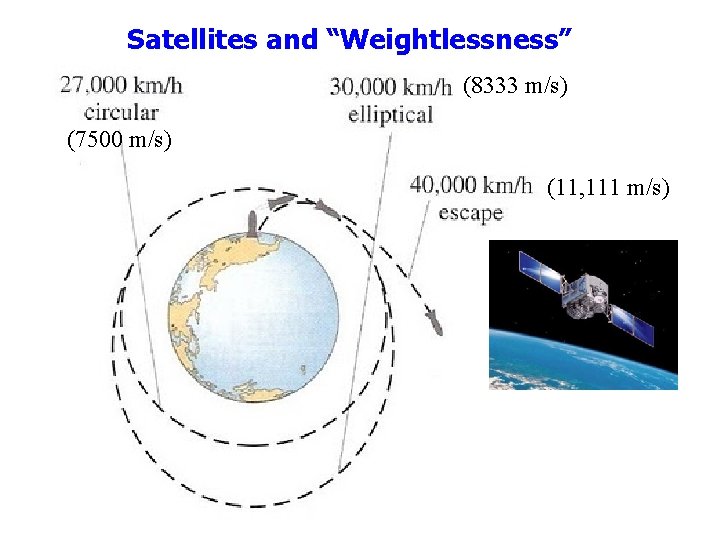
Satellites and “Weightlessness” (8333 m/s) (7500 m/s) (11, 111 m/s)

KEPLER’S LAWS Johannes Kepler (1571 -1630) -German astronomer -Wrote DETAILED description of the motions of the planets based on work of Tycho Brahe (1546 -1601) - Kepler’s work and his Laws of Planetary Motion were indispencable to Newton.

KEPLER’S 3 LAWS OF PLANETARY MOTION Keplers 1 st Law: The path of each planet about the Sun is an ellipse with the Sun at one focus. Keplers 2 nd Law: Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal periods of time. Keplers Laws animation

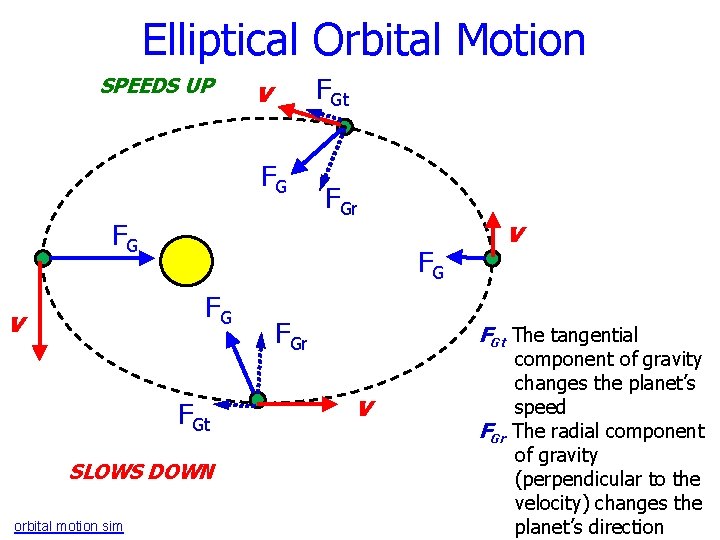
Elliptical Orbital Motion SPEEDS UP FGt v FG FG v FGt SLOWS DOWN orbital motion sim FGr v FGt The tangential v component of gravity changes the planet’s speed FGr The radial component of gravity (perpendicular to the velocity) changes the planet’s direction

KEPLER’S 3 LAWS OF PLANETARY MOTION Keplers 3 rd Law: The ratio of the squares of the periods of any 2 planets revolving about the Sun is equal to the ratio of the cubes of their mean distances from the Sun. That is, OR should be the same for each planet.

Orbital Motion Newton was able to show that Kepler’s laws could be derived from the Law of Gravitation and the Laws of Motion. He used Kepler’s laws as evidence for his Law of Universal Gravitation. FG Kepler’s 3 rd Law

Orbital Motion Jupiter’s Moons Orbital Radius (km) Orbital Period (days) Io Europa Ganymede Callisto 421, 700 671, 034 1, 070, 412 1, 882, 709 1. 77 3. 55 7. 15 16. 69 What is the mass of Jupiter? For all the moons orbiting Jupiter

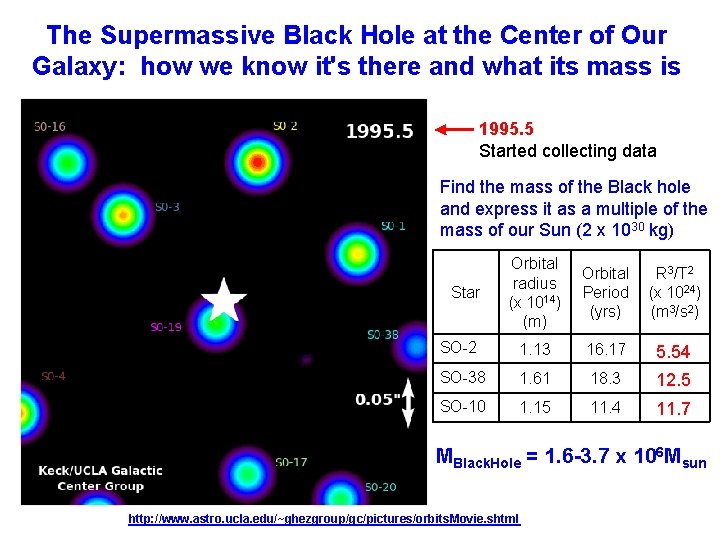
The Supermassive Black Hole at the Center of Our Galaxy: how we know it's there and what its mass is 1995. 5 Started collecting data Find the mass of the Black hole and express it as a multiple of the mass of our Sun (2 x 1030 kg) Star Orbital radius (x 1014) (m) Orbital R 3/T 2 Period (x 1024) (yrs) (m 3/s 2) SO-2 1. 13 16. 17 5. 54 SO-38 1. 61 18. 3 12. 5 SO-10 1. 15 11. 4 11. 7 MBlack. Hole = 1. 6 -3. 7 x 106 Msun http: //www. astro. ucla. edu/~ghezgroup/gc/pictures/orbits. Movie. shtml

Albert Einstein (1879 -1955) - German theoretical physicist - 1921 Nobel Prize in Physics - father of modern physics - Special and general theories of relativity

General Relativity gravity well 8 min clip Brian Greens Universe

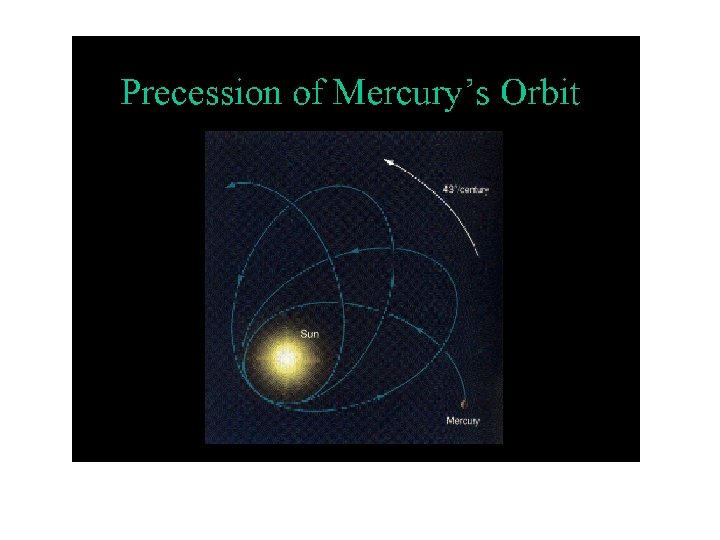
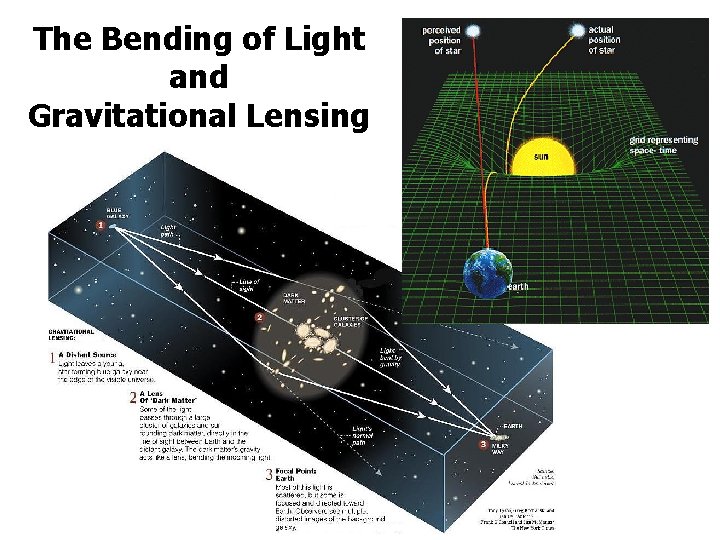
Consequences and Predictions of General Relativity 1. 2. 3. 4. 5. 6. The Bending of Light Precession of Mercury’s Orbit Gravitational Redshift Gravitational Waves Black Holes Expansion of the Universe

The Bending of Light and Gravitational Lensing

Black Holes

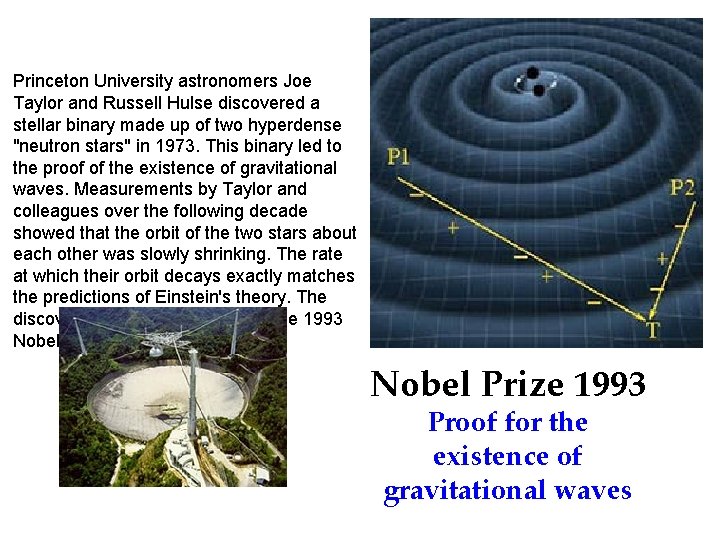
Princeton University astronomers Joe Taylor and Russell Hulse discovered a stellar binary made up of two hyperdense "neutron stars" in 1973. This binary led to the proof of the existence of gravitational waves. Measurements by Taylor and colleagues over the following decade showed that the orbit of the two stars about each other was slowly shrinking. The rate at which their orbit decays exactly matches the predictions of Einstein's theory. The discovery won Hulse and Taylor the 1993 Nobel Prize in Physics. Nobel Prize 1993 Proof for the existence of gravitational waves

Sept. 14, 2015 First Detection of Gravitational Waves!!! Explanation of discovery of gravitational waves Hearing a ripple in Spacetime

Nobel Prize 2011 The expansion of the universe is speeding up