CIRCULAR MOTION AND GRAVITATION Angular Measure Angular Speed

CIRCULAR MOTION AND GRAVITATION Angular Measure, Angular Speed, and Angular Velocity

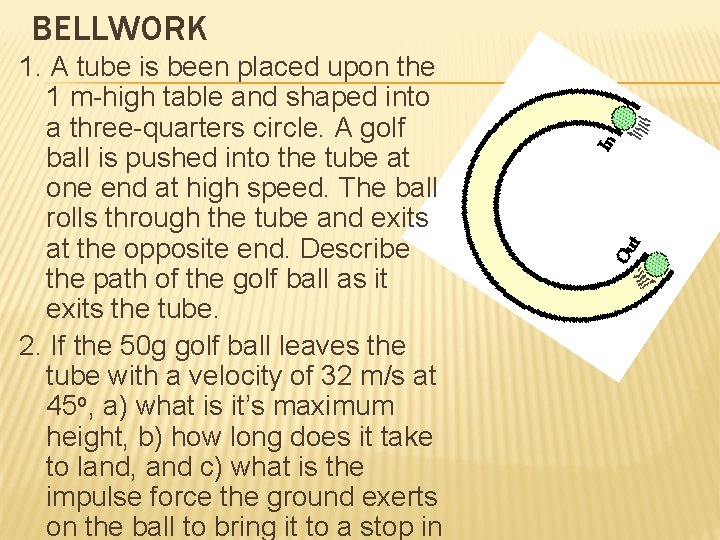
BELLWORK 1. A tube is been placed upon the 1 m-high table and shaped into a three-quarters circle. A golf ball is pushed into the tube at one end at high speed. The ball rolls through the tube and exits at the opposite end. Describe the path of the golf ball as it exits the tube. 2. If the 50 g golf ball leaves the tube with a velocity of 32 m/s at 45 o, a) what is it’s maximum height, b) how long does it take to land, and c) what is the impulse force the ground exerts on the ball to bring it to a stop in

ALGEBRA 2 REVIEW An arc of a circle is a "portion" of the circumference of the circle. � The length of an arc is simply the length of its "portion" of the circumference. Actually, the circumference itself can be considered an arc length. � The length of an arc (or arc length) is traditionally symbolized by s. � The radian measure of a central angle of a circle is defined as the ratio of the length of the arc the angle subtends, s, divided by the radius of the circle, r. �

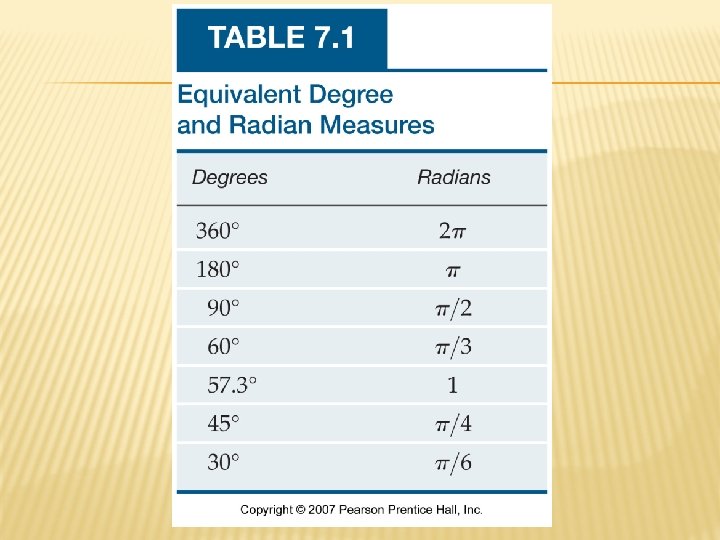
ALGEBRA 2 REVIEW, CONT. � Relationship between Degrees and Radians: � When the arc length equals an entire circumference, we can use s = θr to get 2πr= θr and 2π = θ. � This implies that 2π = 360 o � So and To change from degrees to radians, multiply by To change from radians to degrees, multiply by

EXAMPLE PROBLEMS 1. 2. 3. Convert 50º to radians. Convert π/6 radians to degrees. How long is the arc subtended by an angle of 7π/4 radians on a circle of radius 20. 000 cm? Answers: 1. 5π/18 radians 2. 30 degrees 3. 109. 96 cm

ANGULAR MEASURE � Circular motion is described using polar coordinates, (r, ) � x=rcos and y = rsin , where is measured counterclockwise (ccw) from the positive x-axis. � Angle is defined as = s/r, where s is the arc length, r is the radius, and is the angle in radians. Also expressed as s=r � Angular distance, Δ = - o is measured in degrees or radians. A radian is the angle that subtends an arc length that is equal to the radius (s=r) � 1 rad = 57. 3 o , or 2 rad = 360 o

EXAMPLE 1 � When you are watching the NASCAR Daytona 500, the 5. 5 m long race car subtends an angle of 0. 31 o. What is the distance from the race car to you?

SOLUTION TO EXAMPLE 1

UNIFORM CIRCULAR MOTION IS THE MOTION OF AN OBJECT IN A CIRCLE WITH A CONSTANT OR UNIFORM SPEED. � When moving in a circle, an object traverses a distance around the perimeter of the circle � The distance of one complete cycle around the perimeter of a circle is known as the circumference � This relationship between the circumference of a circle, the time to complete one cycle around the circle, and the speed of the object is merely an extension of the average speed equation

COMBINING KINEMATICS AND CIRCULAR MEASUREMENT TO CALCULATE SPEED � The circumference of any circle can be computed using from the radius according to the equation Circumference = 2*pi*Radius � relating the speed of an object moving in uniform circular motion to the radius of the circle and the time to make one cycle around the circle (period, T), where R=radius:

ANGULAR SPEED AND VELOCITY � Instantaneous angular speed is the magnitude of the instantaneous angular velocity � Tangential (linear) speed angular speed are related to each other through where r is the radius. � The time it takes for an object to go through one revolution is called the period, T. � Then number of revolutions in one second is called the frequency, f

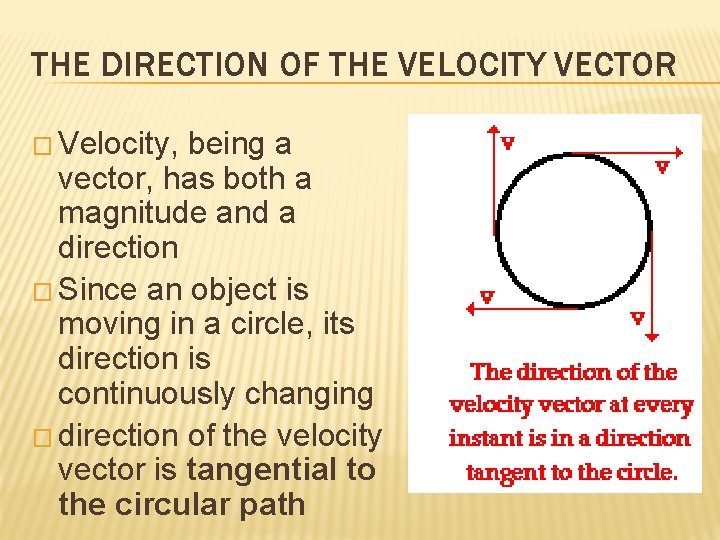
THE DIRECTION OF THE VELOCITY VECTOR � Velocity, being a vector, has both a magnitude and a direction � Since an object is moving in a circle, its direction is continuously changing � direction of the velocity vector is tangential to the circular path

EXAMPLE 2 � A bicycle wheel rotates uniformly through 2. 0 revolutions in 4. 0 s. a) What is the angular speed of the wheel? b) What is the tangential speed of a point 0. 10 m from the center of the wheel? c) What is the period? d) What is the frequency?

ACCELERATION � an accelerating object is an object which is changing its velocity. � a change in either the magnitude or the direction constitutes a change in the velocity. � an object moving in a circle at constant speed is accelerating because the direction of the velocity vector is changing.

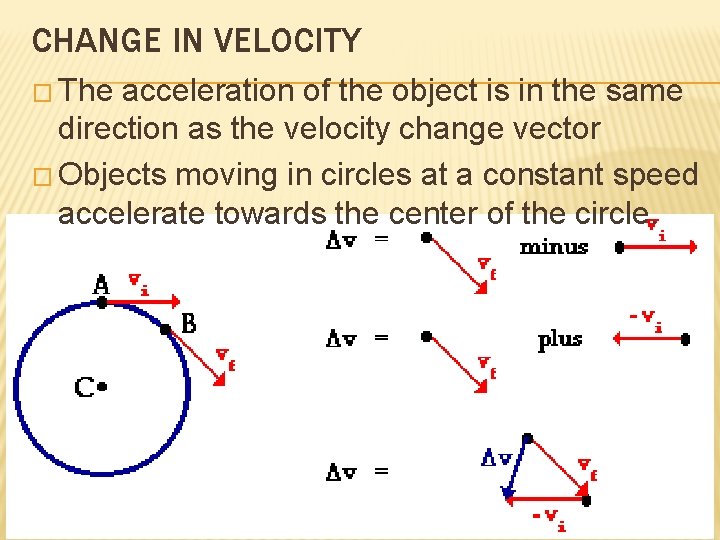
CHANGE IN VELOCITY � The acceleration of the object is in the same direction as the velocity change vector � Objects moving in circles at a constant speed accelerate towards the center of the circle.

CENTRIPETAL ACCELERATION � The linear tangential velocity vector changes direction as the object moves along the circle. � This acceleration is called centripetal acceleration (center-seeking) because it is always directed toward the center of the circle. � The magnitude of centripetal acceleration is given by

CENTRIPETAL FORCE � From Newton’s Second Law, we conclude that there MUST be a net force associated with centripetal acceleration. � Centripetal force is always directed toward the center of the circle since the net force on an object is in the same direction as acceleration.

EXAMPLE 3 � A car of mass 1500 kg is negotiating a flat circular curve of radius 50 m with a speed of 20 m/s. a) What is the source of the centripetal force on the car? Explain b) What is the magnitude of the centripetal acceleration of the car? c) What is the magnitude of the centripetal force on the car? d) What is the minimum coefficient of static friction between the car and the curve?

WARM-UP � Convert the following angles from degrees to radians or from radians to degrees, to two significant figures. v -285 o v 195 o v -90 o v -4/3 π v -270 o v -3/4 π v 165 o v π/3

CONVERT THE FOLLOWING ANGLES FROM DEGREES TO RADIANS OR FROM RADIANS TO DEGREES, TO TWO SIGNIFICANT FIGURES. v -285 o v -5 rad or 1. 6 π v 3. 4 rad or 1. 08 π v 195 o v -90 o v -1. 6 rad or π/2 rad v -4/3 π v -240 o or 4/3 π rad v -270 o v -4. 7 rad or 3/2 π rad v -3/4 π o or 3/4 π rad o v -135 v 165 v 2. 9 rad or 0. 92 π v π/3 rad

EXAMPLE 4: AFTER CLOSING A DEAL WITH A CLIENT, KENT LEANS BACK IN HIS SWIVEL CHAIR AND SPINS AROUND WITH A FREQUENCY OF 0. 5 HZ. WHAT IS KENT’S PERIOD OF SPIN? � Given: f = 0. 5 Hz � Solve: T = 1/f T= 1/0. 5 Hz T= 2 s

EXAMPLE 5: CURTIS’ FAVORITE DISCO RECORD HAS A SCRATCH 12 CM FROM THE CENTER THAT MAKES THE RECORD SKIP 45 TIMES EACH MINUTE. WHAT IS THE LINEAR SPEED OF THE SCRATCH AS IT TURNS? � The record makes 45 revolutions every minute (60 s), so T = 60 s/45 rev. = 1. 3 s � r = 12 cm � v = 2πr/T � = 2π(12 cm)/1. 3 s � = 58 cm/s

EXAMPLE 6: MISSY’S FAVORITE RIDE AT THE TOPSFIELD FAIR IS THE ROTOR , WHICH HAS A RADIUS OF 4. 0 M. THE RIDE TAKES 2. 0 S TO MAKE ON E FULL REVOLUTION. A) WHAT IS MISSY’S LINEAR SPEED ON THE ROTOR? B) WHAT IS MISSY’S CENTRIPETAL ACCELERATION ON THE ROTOR? � Given: r = 4. 0 m, T = 2. 0 s � v=2 pir/T = 2 pi(4. 0 m)/2. 0 s = 13 m/s � ac = v 2/r = 132/4. 0 m = 42 m/s 2

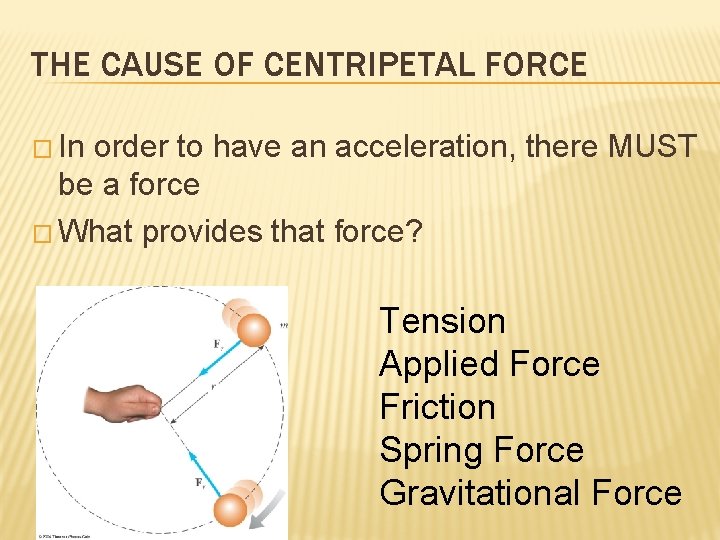
THE CAUSE OF CENTRIPETAL FORCE � In order to have an acceleration, there MUST be a force � What provides that force? Tension Applied Force Friction Spring Force Gravitational Force

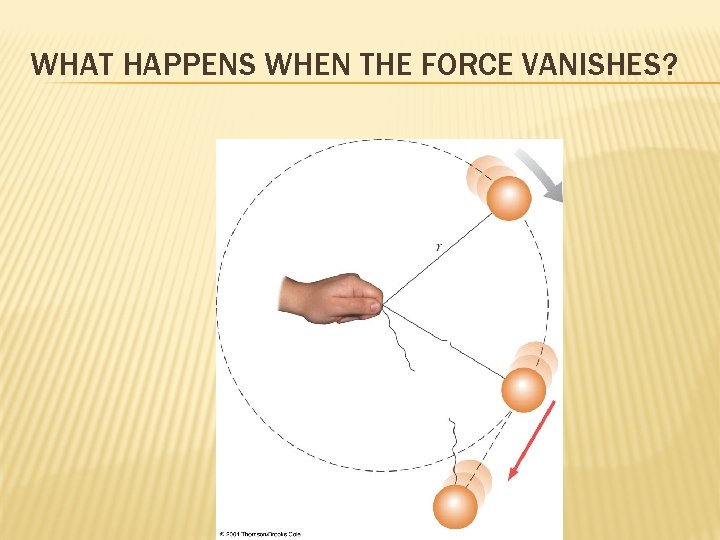
WHAT HAPPENS WHEN THE FORCE VANISHES?

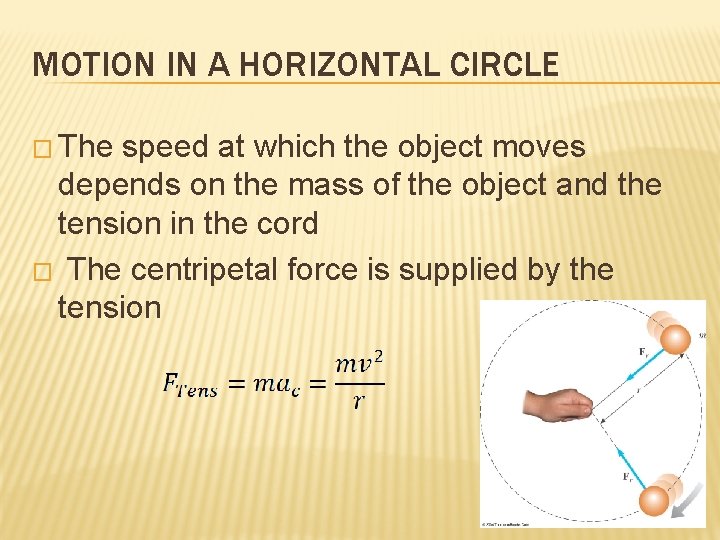
MOTION IN A HORIZONTAL CIRCLE � The speed at which the object moves depends on the mass of the object and the tension in the cord � The centripetal force is supplied by the tension

CIRCULAR MOTION ABOUT A CONICAL PENDULUM � The object is in equilibrium in the vertical direction and undergoes uniform circular motion in the horizontal direction � v is independent of m

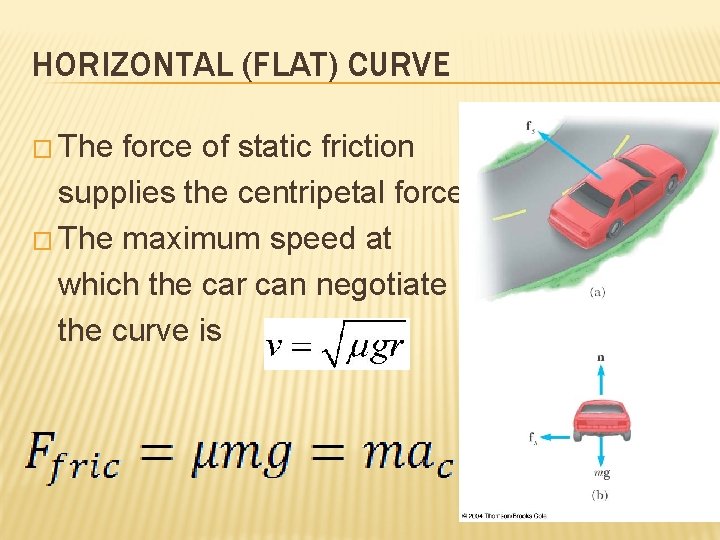
HORIZONTAL (FLAT) CURVE � The force of static friction supplies the centripetal force � The maximum speed at which the car can negotiate the curve is

BANKED CURVE � There is a component of the normal force that supplies the centripetal force

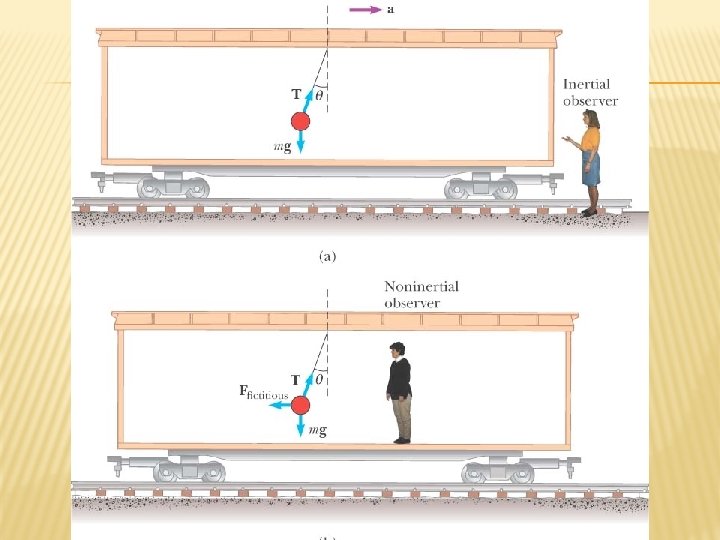
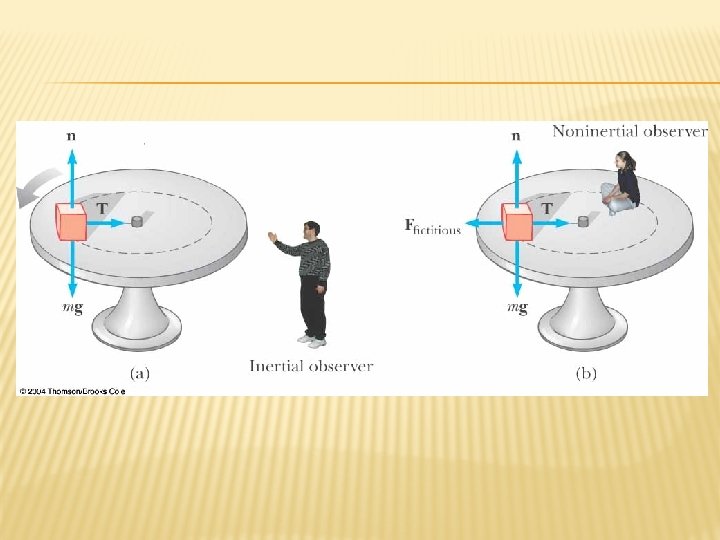
FICTIONAL FORCES � From the frame of the passenger (b), a force appears to push her toward the door � From the frame of the Earth, the car applies a leftward force on the passenger � The outward force is often called a centrifugal force � It is a fictitious force due to the acceleration associated with the car’s change in direction

THE GREAT MISCONCEPTION � Centrifugal, not to be confused with centripetal, means away from the center or outward. � Circular motion leaves the moving person with the sensation of being thrown OUTWARD from the center of the circle rather than INWARD � It’s really just inertia! � http: //www. physicsclassroom. com/mmedia/ci rcmot/cf. cfm

EFFECTS OF “PRETEND” FORCES � Although fictitious forces are not real forces, they can have real effects � Examples: � Objects in the car do slide � You feel pushed to the outside of a rotating platform � The Coriolis force is responsible for the rotation of weather systems and ocean currents

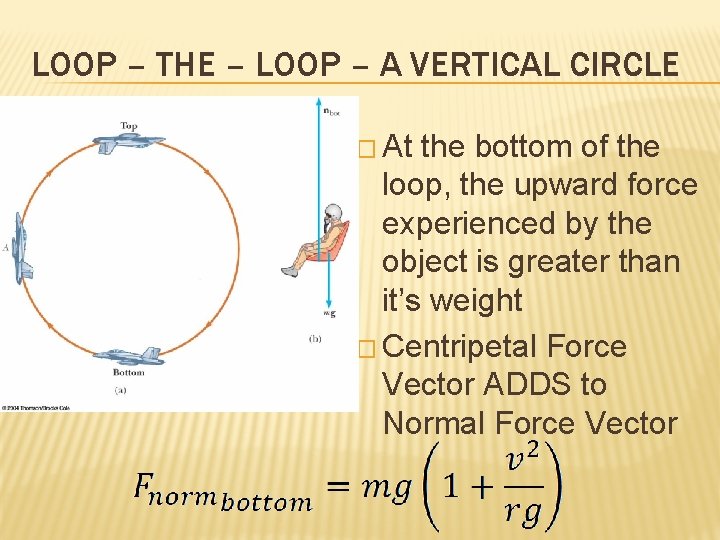
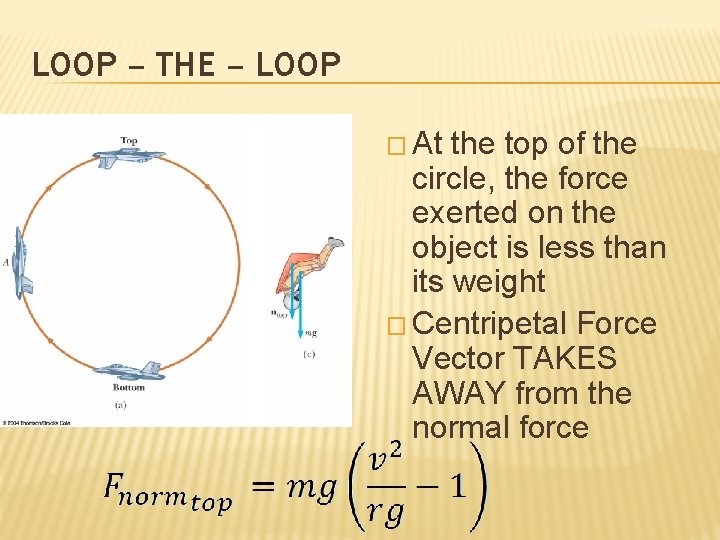
LOOP – THE – LOOP – A VERTICAL CIRCLE � At the bottom of the loop, the upward force experienced by the object is greater than it’s weight � Centripetal Force Vector ADDS to Normal Force Vector

LOOP – THE – LOOP � At the top of the circle, the force exerted on the object is less than its weight � Centripetal Force Vector TAKES AWAY from the normal force

WARM-UP: Captain Chip, the pilot of a 60500 kg jet plane, is told he must remain in a holding pattern over the airport until it is his turn to land. If Captain Chip flies his plane in a circle whose radius is 50. 0 km once every 30. 0 min, what centripetal force must the air exert against the wings to keep the plane moving in a circle?

EXAMPLE 7. 45 � Many racetracks have banked turns, which allow the cars to travel faster around the curves than if the curves were flat. Actually, cars could also make turns on these banked curves if there were no friction at all. � Use a free body diagram to explain how this is possible.

EXAMPLE 7. 46 � An indy car with a speed of 120 km/hr goes around a level, circular track with a radius of 1. 00 km. What is the centripetal acceleration of the car? A. 1. 11 m/s 2 B. 0. 555 m/s 2 C. 3. 49 m/s 2 D. 7. 54 m/s 2.

EXAMPLE 7. 52 � A car with a constant speed of 83. 0 km/hr enters a circular flat curve with a radius of curvature of 0. 400 km. If the friction between the road and the car’s tires can supply a centripetal acceleration of 1. 25 m/s 2 does the car negotiate the curve safely? Justify your answer. A. Yes B. No

EXAMPLE 7. 53 � A student is to swing a bucket of water in a vertical circle without spilling any ( Fig. 7. 29). (a) Use a free body diagram to help explain how this task is possible (what provides the centripetal force? ). (b) If the distance from his shoulder to the center of mass of the bucket of water is 1. 0 m, what is the minimum speed required to keep the water from coming out of the bucket at the top of the swing?

EXAMPLE 7. 58 � For a scene in a movie, a stunt driver drives a 1. 50 x 103 kg SUV with a length of 4. 25 m around a circular curve with a radius of curvature of 0. 333 km ( Fig. 7. 31). The vehicle is to be driven off the edge of a gully 10. 0 m wide, and land on the other side 2. 96 m below the initial side. What is the minimum centripetal acceleration the truck must have in going around the circular curve to clear the gully and land on the other side?

BELLWORK: BONNIE IS ICE SKATING AT THE OLYMPIC GAMES. SHE IS MAKING A SHARP TURN WITH A RADIUS OF 22. 6 M AND WITH A SPEED OF 16. 1 M/S. USE NEWTON'S SECOND LAW TO DETERMINE THE ACCELERATION AND THE ANGLE OF LEAN OF BONNIE'S 55. 0 -KG BODY. Given Info: m = 55. 0 kg v = 16. 1 m/s r = 22. 6 m Find: a = ? ? ? Angle of lean = ? ? ?

SOLUTION TO BELLWORK � ac = v 2/R a = (16. 1 m/s)2/(22. 6 m) = 11. 5 m/s 2 � Fx = Fnet = m • a Fx = (55. 0 kg) • (11. 5 m/s/s) = 631 N �

ANGULAR ACCELERATION: NON-UNIFORM CIRCULAR MOTION � Angular acceleration = the rate of change of angular velocity

EXAMPLE 8: A ROTATING CD � A CD accelerates uniformly from rest to its operational speed of 500 rpm in 3. 50 s. A. What is the angular acceleration of the CD during this time? B. What is the angular velocity of the CD after this time? The angular acceleration after this time? C. If the CD comes uniformly to a stop in 4. 50 s, what is its angular acceleration during that part of the motion?

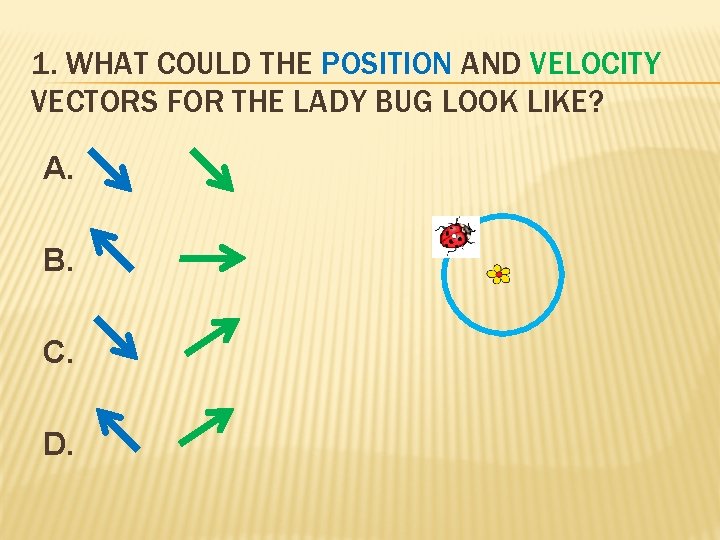
1. WHAT COULD THE POSITION AND VELOCITY VECTORS FOR THE LADY BUG LOOK LIKE? A. B. C. D.

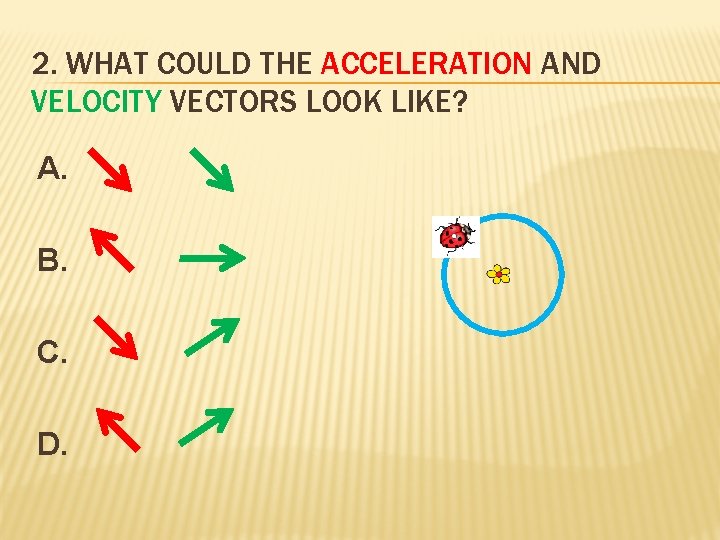
2. WHAT COULD THE ACCELERATION AND VELOCITY VECTORS LOOK LIKE? A. B. C. D.

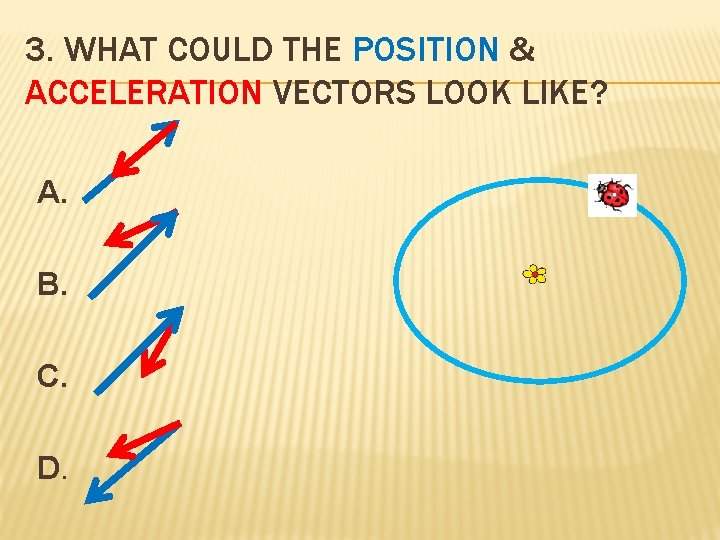
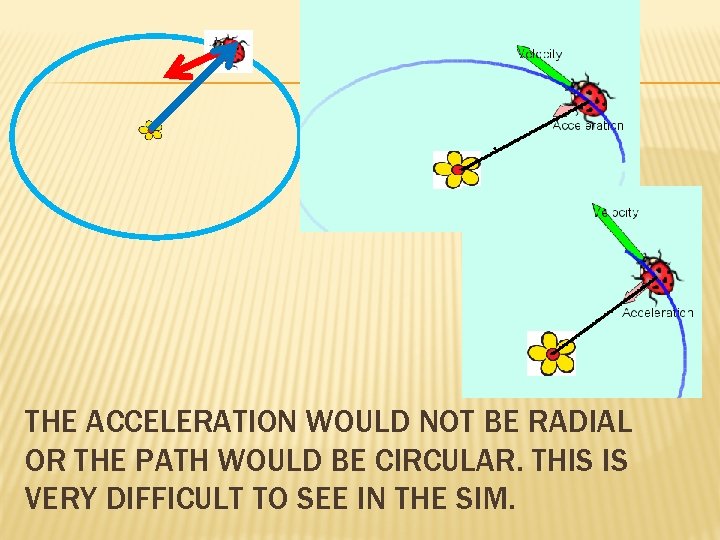
3. WHAT COULD THE POSITION & ACCELERATION VECTORS LOOK LIKE? A. B. C. D.

THE ACCELERATION WOULD NOT BE RADIAL OR THE PATH WOULD BE CIRCULAR. THIS IS VERY DIFFICULT TO SEE IN THE SIM.

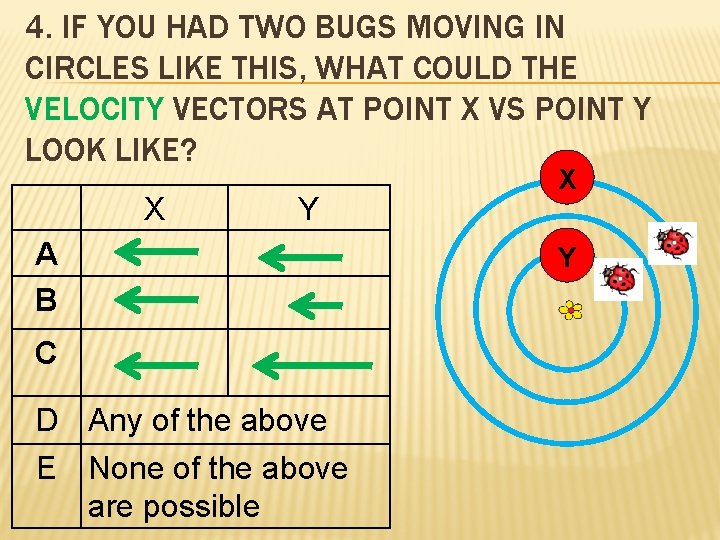
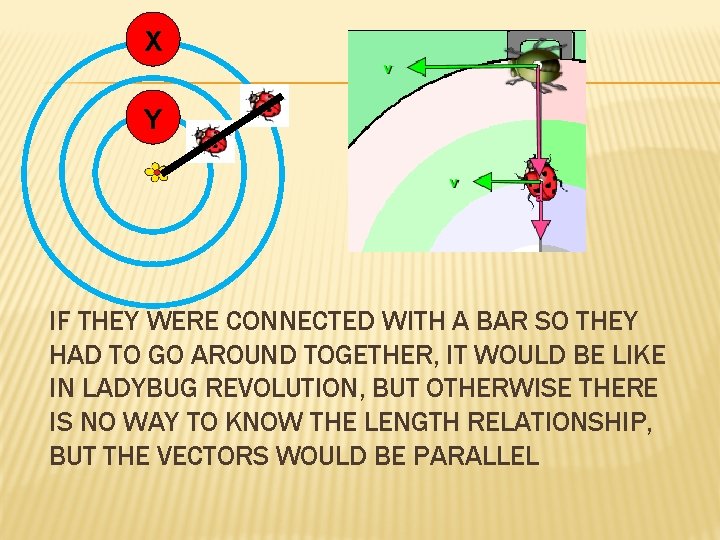
4. IF YOU HAD TWO BUGS MOVING IN CIRCLES LIKE THIS, WHAT COULD THE VELOCITY VECTORS AT POINT X VS POINT Y LOOK LIKE? X Y A B C D Any of the above E None of the above are possible X Y

X Y IF THEY WERE CONNECTED WITH A BAR SO THEY HAD TO GO AROUND TOGETHER, IT WOULD BE LIKE IN LADYBUG REVOLUTION, BUT OTHERWISE THERE IS NO WAY TO KNOW THE LENGTH RELATIONSHIP, BUT THE VECTORS WOULD BE PARALLEL

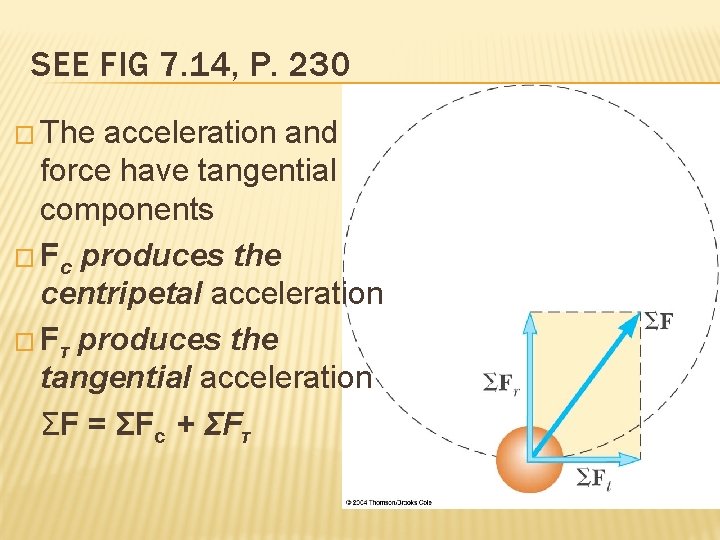
SEE FIG 7. 14, P. 230 � The acceleration and force have tangential components � Fc produces the centripetal acceleration � Fτ produces the tangential acceleration ΣF = ΣFc + ΣFτ

TANGENTIAL ACCELERATION � The tangential acceleration is the rate of change of tangential velocity � For non-uniform circular motion, there are angular and tangential acceleration. � The total acceleration is the vector sum of the tangential and centripetal accelerations.

EXAMPLE 7. 60 THE ANGULAR ACCELERATION IN CIRCULAR MOTION : � (a) is equal in magnitude to the tangential acceleration divided by the radius � (b) increases the angular velocity if both angular velocity and angular acceleration are in the same direction � (c) has units of s-2 � (d) all of the preceding.

EXAMPLE 7. 62: FOR UNIFORM CIRCULAR MOTION, � (a) α = 0 � (b) ω = 0 � (c) r = 0 � (d) none of the preceding.

EXAMPLE 7. 66 � During an acceleration, the angular speed of an engine increases from 600 rpm to 2500 rpm in 3. 0 s. What is the average angular acceleration of the engine?

TORQUE: MEASUREMENT OF THE TENDENCY OF A FORCE TO PRODUCE A ROTATION ABOUT AN AXIS. � Torque = perpendicular force x lever arm τ=F x d � d = distance from the pivot point, or fulcrum, to the point where the component of the force perpendicular to the lever arm is being exerted � The longer the lever arm, the larger the torque

� Counterclockwise rotation = POSITIVE τ � Clockwise rotation = NEGATIVE τ � Units = Newton x meter = Nm (but NOT equal to Joules because torque is not a form of energy) � NOTE: weight is a force that can produce torque if the object is not supported at its center of gravity.

EXAMPLE 1 � Ned tightens a bolt in his car engine by exerting 12 N of force on his wrench at a distance of 0. 40 m from the fulcrum. How much torque must Ned produce to turn the bolt?

EXAMPLE 2: � Mabel and Maude are seesawing on the school playground and decide to see if they can move to the correct location to make the seesaw balance. Mabel weighs 400 N and she sits 2. 00 m from the fulcrum of the seesaw. Where should 450 -N Maude sit to balance the seesaw?

ANGULAR MOMENTUM: MEASURE OF HOW DIFFICULT IT IS TO STOP A ROTATING OBJECT � Moment of Inertia: The resistance of an object to changes in its rotational motion moment of inertia = (mass)(radius)2 I = mr 2 � SI Units = kilogram meter squared = kgm 2 � An object that is rotating tends to continue to spinning at a constant rate unless acted on by an unbalanced force to alter that rotation

MOMENT OF INERTIA FOR VARIOUS SHAPES Hoop rotating about its center Hoop rotating about its diameter Solid cylinder Stick rotating about its center of gravity Stick rotating about its end Solid sphere rotating about its center of gravity I=mr 2 I = ½ mr 2 I = 1/12 ml 2 I = 1/3 ml 2 I = 2/5 mr 2

ANGULAR MOMENTUM Angular momentum = (mass)(velocity)(radius) L = mvr � SI Units = kilogram meter 2 per second 2 � kgm 2/s 2 � The product of the mass and the velocity for an object rotating at a distance, r, from the axis. � Angular Momentum of a system is conserved when no outside forces are acting

EXAMPLE 3 � On the Wheel of Fortune game show, Ian spins the 15. 0 kg wheel that has a radius of 1. 40 m. What is the moment of inertia of this disk-shaped wheel? (thin cylinder)

EXAMPLE 4 � Jun is twirling her 0. 60 m majorette’s baton that has a mass of 0. 40 kg. What is the moment of inertia of the baton as it spins about its center of gravity?

EXAMPLE 5 At Wellesley College in Massachusetts there is a favorite tradition called hoop rolling. In their caps and gowns, seniors roll wooden hoops in a race in which the winner is said to be the first in the class to marry. Hilary rolls her 0. 2 kg hoop across the finish line. The moment of inertia of the hoop is 0. 032 kgm 2. What is the radius of

EXAMPLE 6 � Jupiter orbits the sun with a speed of 2079 m/s at an average distance of 71, 398, 000 m. If Jupiter has a mass of 1. 90 x 1027 kg, what is its angular momentum as it orbits?