Circular motion All turns are a combination of

Circular motion

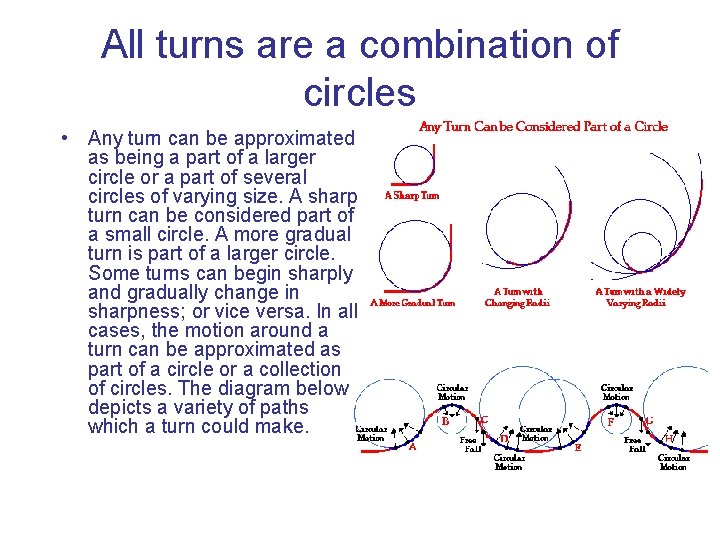
All turns are a combination of circles • Any turn can be approximated as being a part of a larger circle or a part of several circles of varying size. A sharp turn can be considered part of a small circle. A more gradual turn is part of a larger circle. Some turns can begin sharply and gradually change in sharpness; or vice versa. In all cases, the motion around a turn can be approximated as part of a circle or a collection of circles. The diagram below depicts a variety of paths which a turn could make.

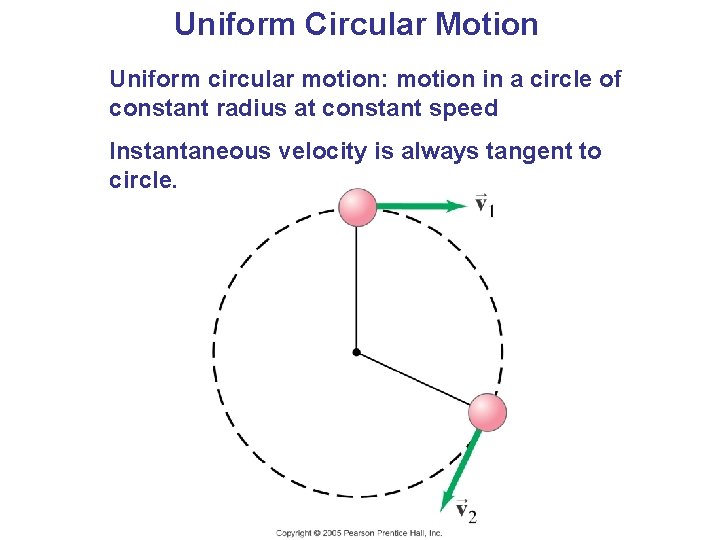
Uniform Circular Motion Uniform circular motion: motion in a circle of constant radius at constant speed Instantaneous velocity is always tangent to circle.

Linear and Rotational Speed • Linear speed is the distance traveled per unit of time. speed = Δd/Δt • Tangential speed is the radial distance time the rotational speed. tangential speed = rxω • Rotational speed (or angular speed) is the number of rotations per unit of time. rotation speed = ω = 2π*frequency

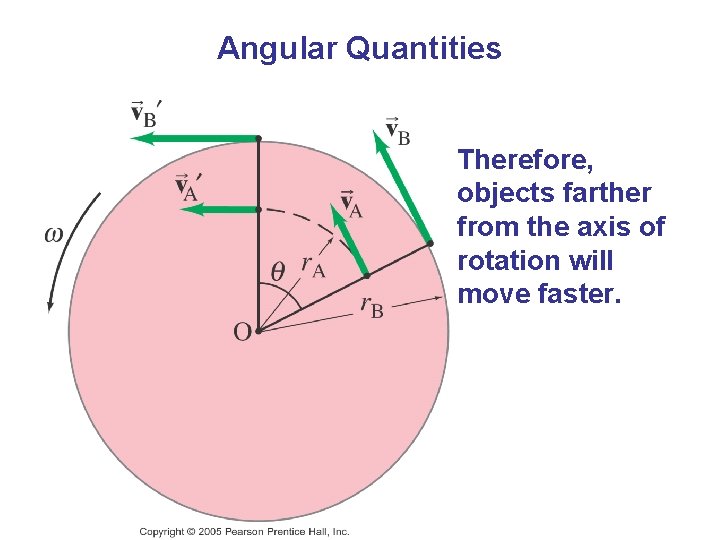
Angular Quantities Therefore, objects farther from the axis of rotation will move faster.

Rotational Speed • All parts of any rigid object have the same rotational speed, but tangential or linear speed depends on the distance to the axis of rotation

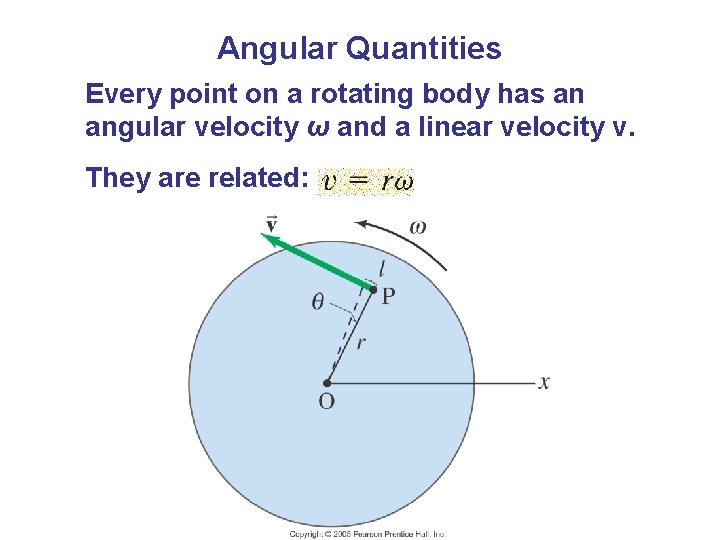
Angular Quantities Every point on a rotating body has an angular velocity ω and a linear velocity v. They are related:

Question • What part of the Earth’s surface has the greatest rotational velocity? r R

Rotational Velocity r R The rotational velocity is the same everywhere, the earth rotates once each day , so ω = 2π/day.

Question • What part of the Earth’s surface has the greatest linear (or tangential) velocity? r R

Linear Velocity r R The linear velocity is greatest at the equator because the distance to the axis of rotation is greatest at the equator, linear velocity is given by the product of the rotational velocity and the distance to the axis of rotation

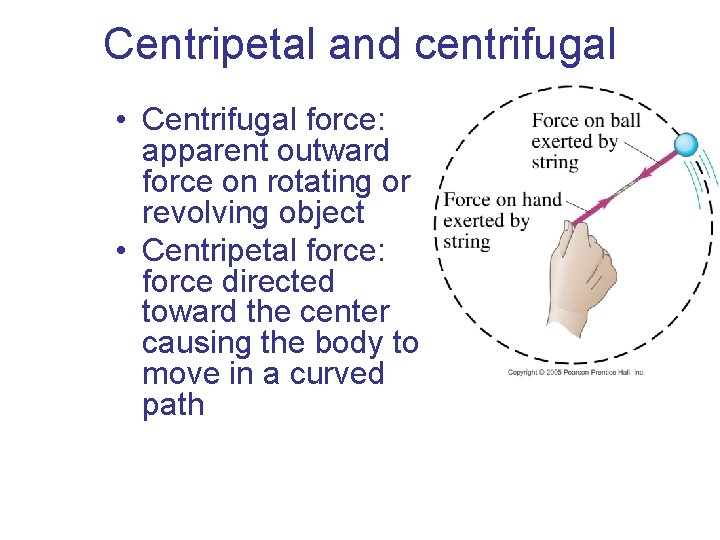
Centripetal and centrifugal • Centrifugal force: apparent outward force on rotating or revolving object • Centripetal force: force directed toward the center causing the body to move in a curved path

Uniform Circular Motion This acceleration is called the centripetal, or radial, acceleration, and it points towards the center of the circle.

What is the direction of the force that acts on clothes in the spin cycle of a washing machine? a. Inward b. Down c. Outward d. Up Hint they are moving in a circular path.

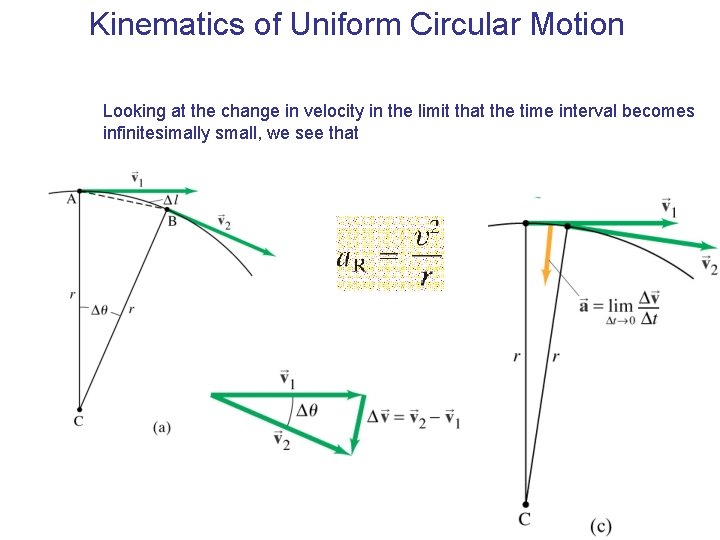
Kinematics of Uniform Circular Motion Looking at the change in velocity in the limit that the time interval becomes infinitesimally small, we see that

Centripetal Acceleration The centripetal acceleration of an object moving in a circular path is given by: a = v 2/r Where v is the tangential or linear velocity and r is the radius of curvature

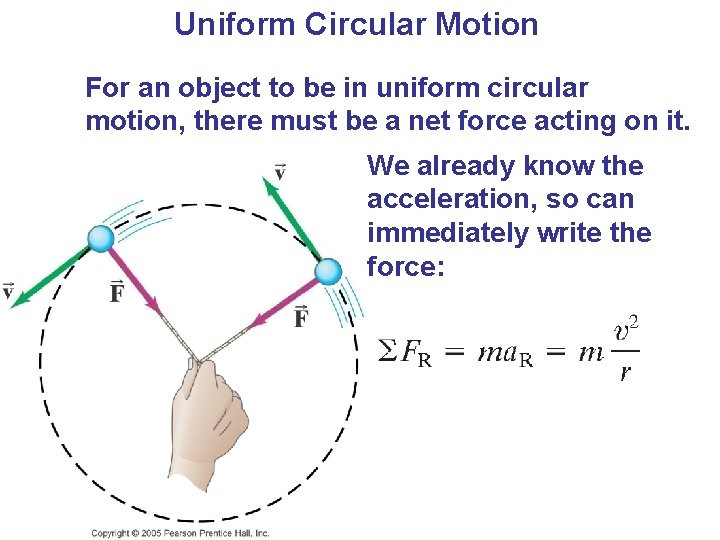
Uniform Circular Motion For an object to be in uniform circular motion, there must be a net force acting on it. We already know the acceleration, so can immediately write the force:

• There are three mathematical quantities which will be of primary interest to us as we analyze the motion of objects in circles. These three quantities are speed, acceleration and force. • The acceleration of an object moving in a circle can be determined by either two of the following equations.

Centripetal Force Problem Solving • The process of solving a circular motion problem is much like any other problem in physics class. The process involves a careful reading of the problem, the identification of the known and required information in variable form, the selection of the relevant equation(s)

Centripetal Force • Centripetal force is the force that causes an object to move in a circular path or arc. • The centripetal force is directed toward the center of the arc, it is perpendicular to the instantaneous velocity. • Fcent = mv 2/r = mω2 r

Uniform Circular Motion There is no centrifugal force pointing outward; what happens is that the natural tendency of the object to move in a straight line must be overcome. If the centripetal force vanishes, the object flies off tangent to the circle

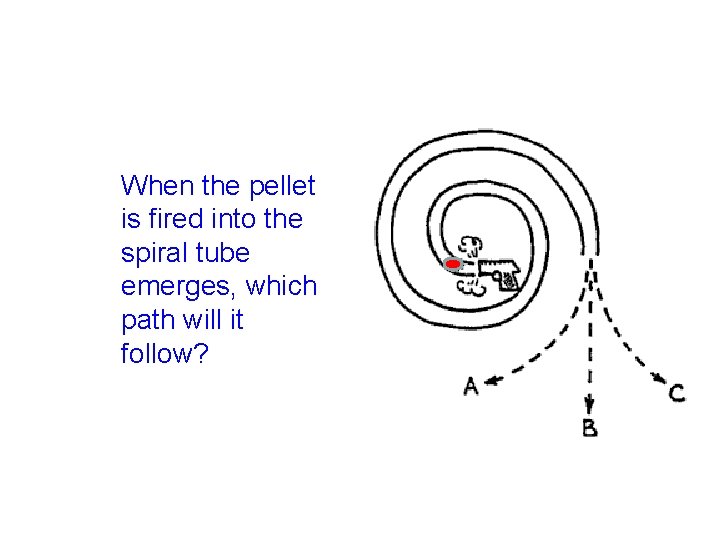
When the pellet is fired into the spiral tube emerges, which path will it follow?

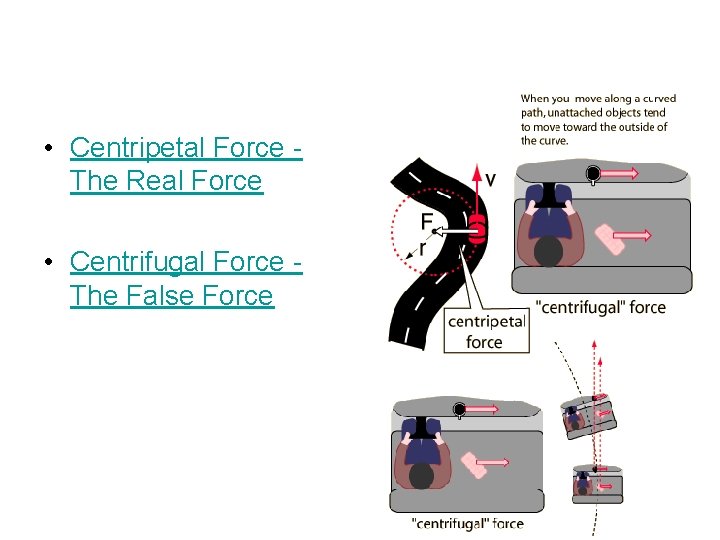
• Centripetal Force The Real Force • Centrifugal Force The False Force

Nonuniform Circular Motion If an object is moving in a circular path but at varying speeds, it must have a tangential component to its acceleration as well as the radial one.

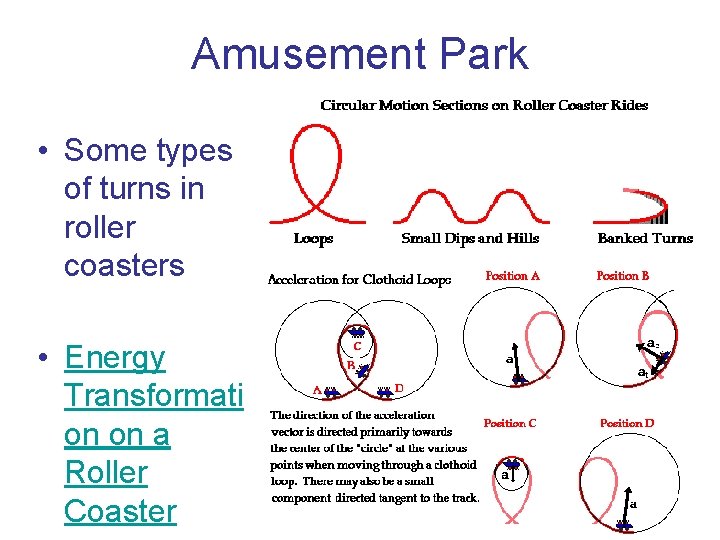
Amusement Park • Some types of turns in roller coasters • Energy Transformati on on a Roller Coaster

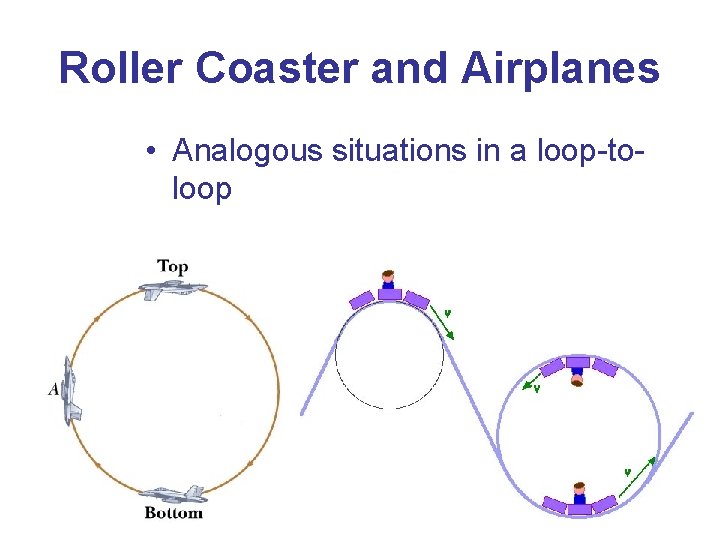
Roller Coaster and Airplanes • Analogous situations in a loop-toloop

At the top of the Hill The only forces acting on the rider are the upward normal force n exerted by the car and the downward force of gravity w, the rider's weight. These add together, as vectors, to provide the net force Fnet which is the centripetal force Fc, directed toward the center of the circle

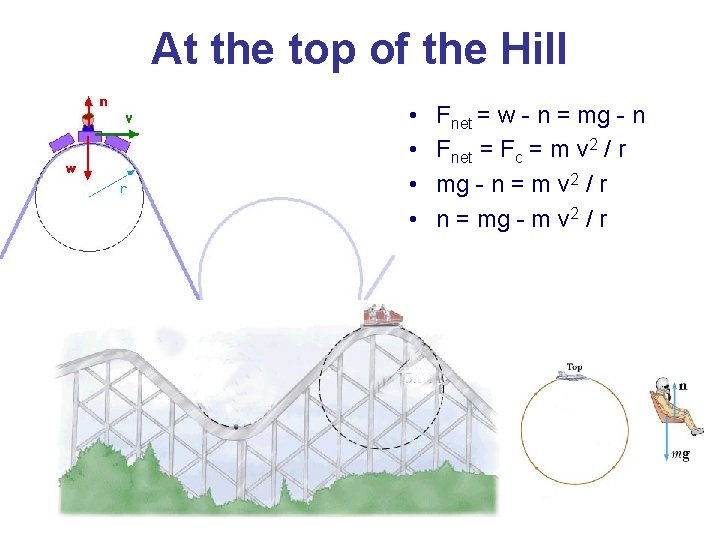
At the top of the Hill • • Fnet = w - n = mg - n Fnet = Fc = m v 2 / r mg - n = m v 2 / r n = mg - m v 2 / r

At the top of the Hill • What does all this mean? The normal force or the rider's apparent weight is less than the rider's real weight. The seat can not exert a negative force on the rider. If we approach a situation where the apparent weight might become negative, there should be a good safety restraint system -- seat belts, lap bars, shoulder restraints, or something of that sort. • We might ask how fast the coaster can go until the rider just (barely) looses contact with the seat. That means the normal force between seat and rider is zero. That occurs for • n = mg - m v 2 / r = 0 • m v 2 / r = mg • v 2/ r = g

At the bottom of the Hill The only forces acting on the rider are the upward normal force n exerted by the car and the downward force of gravity w, the rider's weight. These add together, as vectors, to provide the net force Fnet which is the centripetal force Fc, directed toward the center of the circle

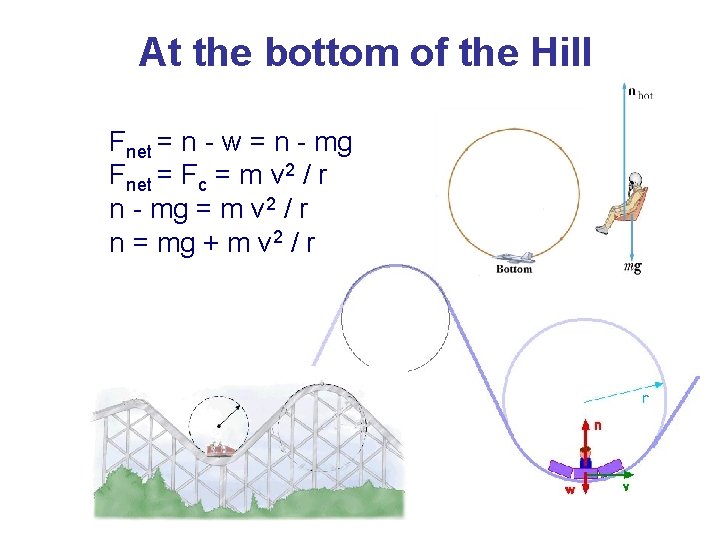
At the bottom of the Hill Fnet = n - w = n - mg Fnet = Fc = m v 2 / r n - mg = m v 2 / r n = mg + m v 2 / r

At the bottom of the Hill What does all this mean? • The normal force or the rider's apparent weight is now more than the rider's real weight. The rider feels pressed down into the seat. The rider's hands and arms are hard to move. The rider's blood is even hard to move. Airplane pilots are in this situation as they pull out of a dive. The ratio of this "apparent weight" to real weight may be described as the apparent effect of gravity or may be described as "g-forces" of six or seven -meaning an apparent weight of six or seven times one's real weight -- can mean that enough blood will not be circulated to the brain and a pilot -- or other passenger -may pass out.

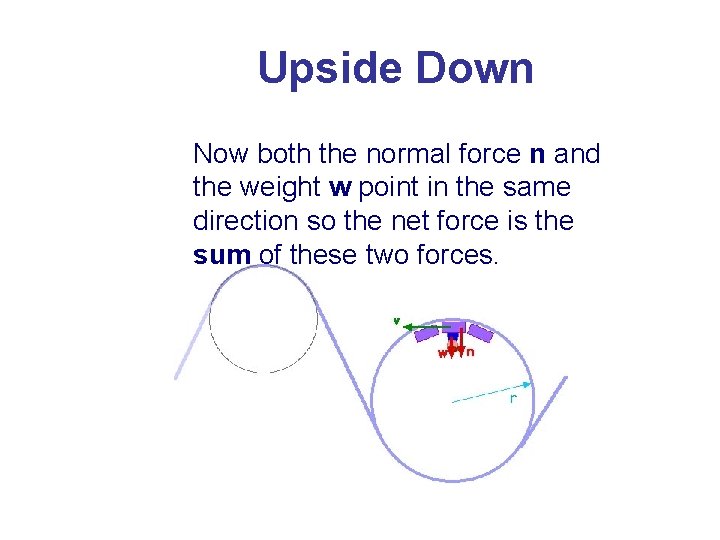
Upside Down Now both the normal force n and the weight w point in the same direction so the net force is the sum of these two forces,

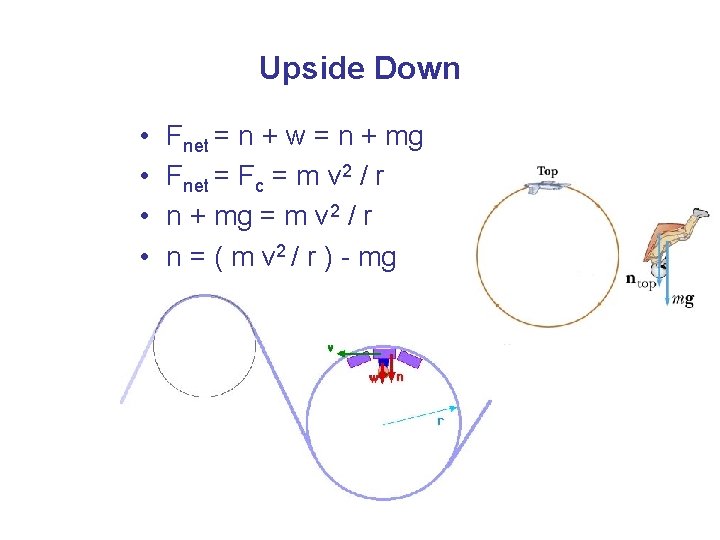
Upside Down • • Fnet = n + w = n + mg Fnet = Fc = m v 2 / r n + mg = m v 2 / r n = ( m v 2 / r ) - mg

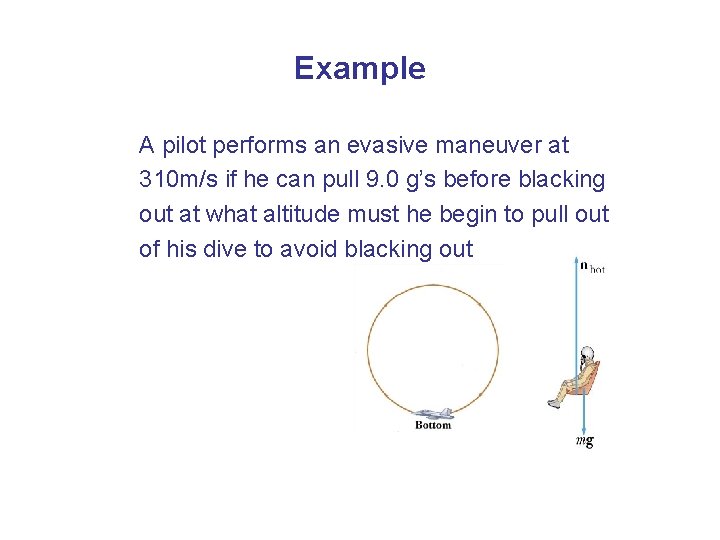
Example A pilot performs an evasive maneuver at 310 m/s if he can pull 9. 0 g’s before blacking out at what altitude must he begin to pull out of his dive to avoid blacking out

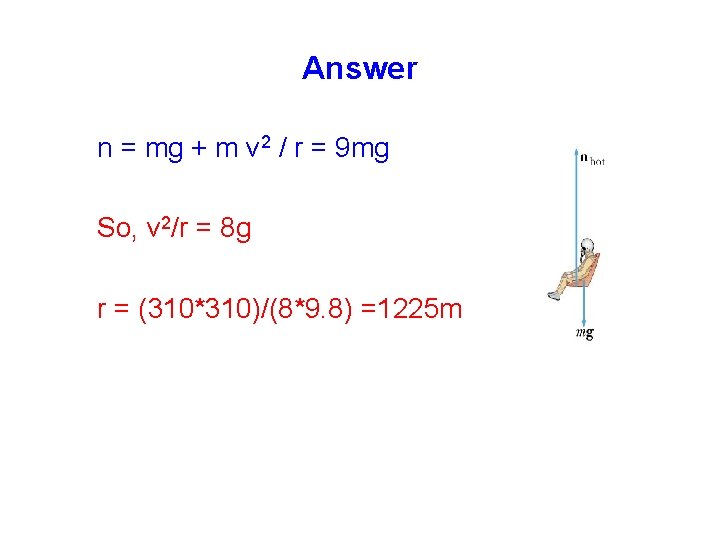
Answer n = mg + m v 2 / r = 9 mg So, v 2/r = 8 g r = (310*310)/(8*9. 8) =1225 m

Highway Curves, Banked and Unbanked If the frictional force is insufficient, the car will tend to move more nearly in a straight line, as the skid marks show.

• The Cajun Cliffhanger at Great America is a ride in which occupants line the perimeter of a cylinder and spin in a circle at a high rate of turning. When the cylinder begins spinning very rapidly, the floor is removed from under the riders' feet. What affect does a doubling in speed have upon the centripetal force? Explain. Doubling the speed of the ride will cause the force to be four times greater than the original force. According to the equation Fnet=(m • v 2) / R, force and speed 2 are directly proportional. So 2 X the speed means 4 X the force (that's from 22).

A car travels in a circle with constant speed. The net force on the car a. is zero because the car is not accelerating b. is directed in the direction of travel c. is directed toward the center of the curve d. none of the above

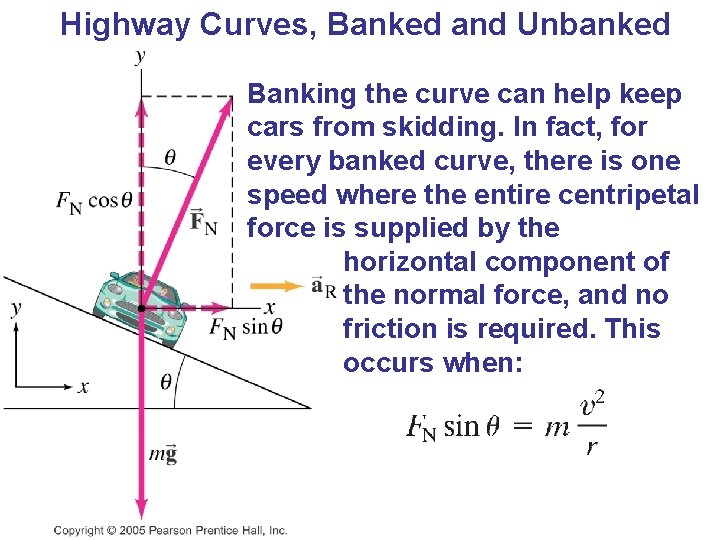
Highway Curves, Banked and Unbanked Banking the curve can help keep cars from skidding. In fact, for every banked curve, there is one speed where the entire centripetal force is supplied by the horizontal component of the normal force, and no friction is required. This occurs when:

A 945 -kg car makes a 180 -degree turn with a speed of 10. 0 m/s. The radius of the circle through which the car is turning is 25. 0 m. Determine the force of friction and the coefficient of friction acting upon the car. Known Information: m = 945 kg v = 10. 0 m/s R = 25. 0 m Requested Information: Ffrict = ? ? ? mu = ? ? ("mu" - coefficient of friction) Fnet = 3600 N Ffrict = 3600 N μ = Ffrict/ Fnorm μ = 0. 389

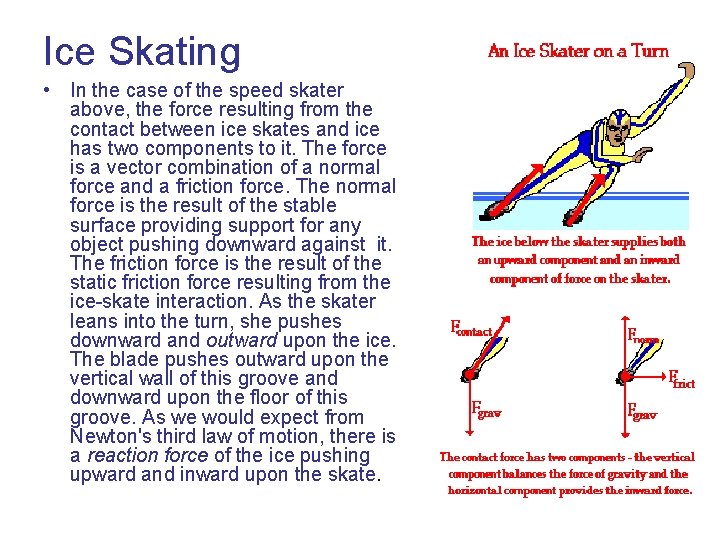
Ice Skating • In the case of the speed skater above, the force resulting from the contact between ice skates and ice has two components to it. The force is a vector combination of a normal force and a friction force. The normal force is the result of the stable surface providing support for any object pushing downward against it. The friction force is the result of the static friction force resulting from the ice-skate interaction. As the skater leans into the turn, she pushes downward and outward upon the ice. The blade pushes outward upon the vertical wall of this groove and downward upon the floor of this groove. As we would expect from Newton's third law of motion, there is a reaction force of the ice pushing upward and inward upon the skate.

More Turns • A downhill skier makes her turn by leaning into the snow. The snow pushes back in both an inward an upward direction - balancing the force of gravity and supplying the centripetal force. A football player makes his turn by leaning into the ground. The ground pushes back in both an inward and upward direction - balancing the force of gravity and supplying both the centripetal force. A cyclist makes his turn in a similar manner as he leans at an angle to the horizontal. The road surface pushes with an upward component of force to balance the downward force of gravity. The road surface also pushes with a horizontal component of force towards the center of the circle through which the cyclist is turning. A turn is only possible when there is a component of force directed towards the center of the circle about which the person is moving.

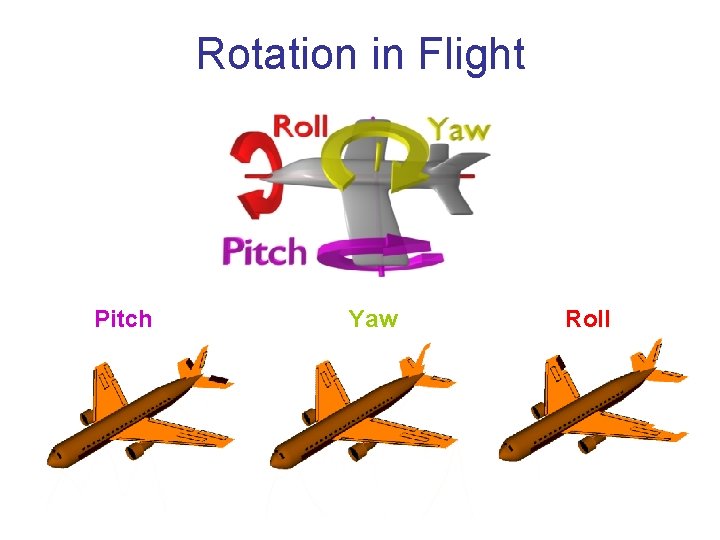
Rotation in Flight Pitch Yaw Roll

• BLUE ANGELS - Insane Footage Takes You Inside the Cockpit - Bing video • Best Blue Angels Music Video: "Pump Up The Angels" - Bing video

You. Tube aerobatics by 747 Military Channel : : Video : : Blue Angels

Multiple Choice A dragonfly is sitting on a merry-go-round 2. 8 m from the center. If the tangential velocity of the ride is 0. 89 m/s, what is the centripetal acceleration of the dragonfly? A. 0. 11 m/s 2 B. 0. 28 m/s 2 C. 0. 32 m/s 2 D. 2. 2 m/s 2

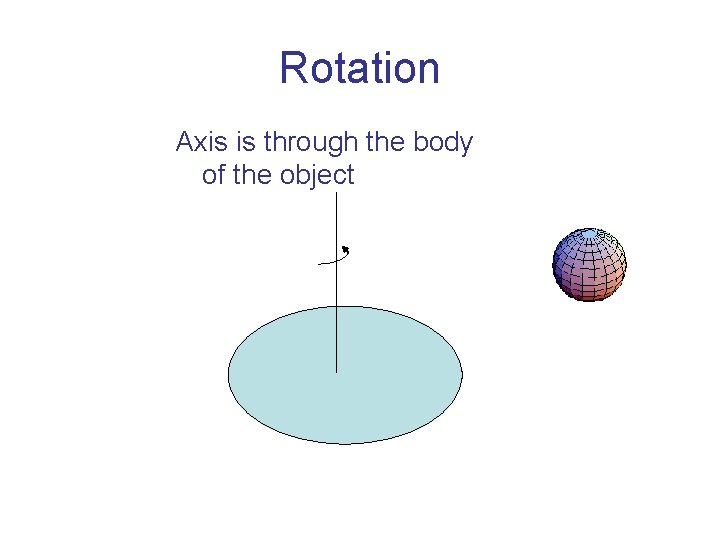
Rotation Axis is through the body of the object

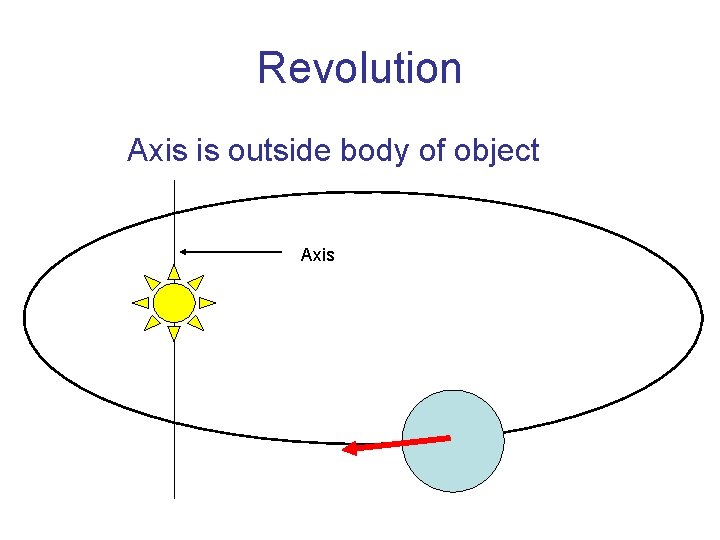
Revolution Axis is outside body of object Axis

Rotation and Revolution • Rotation (spin) occurs when the axis about which an object rotates passes through the object, e. g. the Earth rotates about an axis that passes through the poles. • Revolution occurs when the axis is external to the body in motion. • Earth Rotates once in 24 hours • Earth revolves around the sun one time in 365. 25 days.

Rotation and Revolution Do the people on a ferris wheel revolve or rotate? The people revolve since the axis is the center of the Ferris wheel. Does the Ferris wheel rotate or revolve? The Ferris wheel rotates, the axis passes through its center.