Circuits and Circuit Elements 1 Electric Circuits An

Circuits and Circuit Elements 1

Electric Circuits Ø An electric circuit is any closed path along which electrons can flow. Ø For a continuous flow of electrons through a circuit, there must be no gaps (such as an open electric switch).

Electric Circuits Ø Devices connect to a circuit in one of two ways: • Series • Parallel

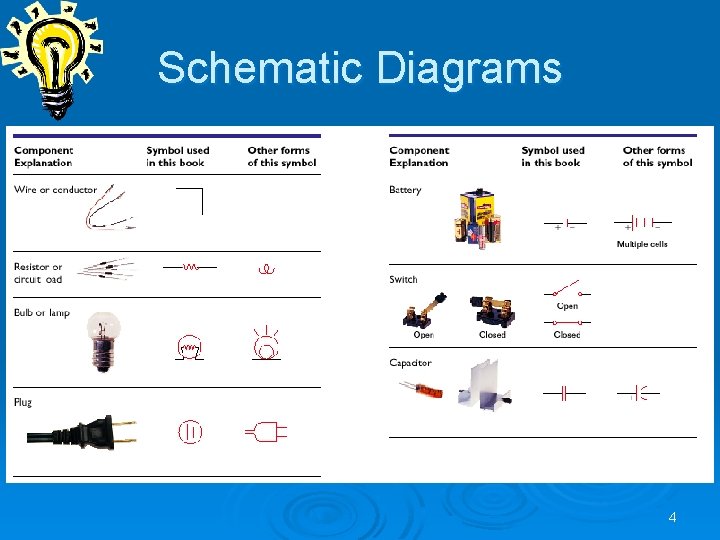
Schematic Diagrams 4

Series Circuits A single-pathway circuit is formed for electron flow between the terminals of the battery, generator, or wall socket. Ø A break anywhere in the path results in an open circuit; electron flow ceases. Total resistance adds and current decreases as more devices are added. Ø Main disadvantage: If one device fails, the entire circuit ceases, and none of the devices will operate. Ø

Resistors in Series Ø Resistors in Series have the same current. Ø When many resistors are connected in series, the current in each resistor is the same. Ø To find the total current in a series circuit, find the EQUIVALENT RESISTANCE of the circuit and plug that into V=IR. 6

Equivalent Resistance - Series The EQUIVALENT RESISTANCE in a series circuit is the SUM of the circuit’s resistances. Ø Req = R 1 + R 2 + R 3…. . Ø 7

EXAMPLE: Find the current through the circuit below 1. 5 3. 0 9 V Ø Step 1: Find Equivalent Resistance Ø Req = 1. 5 + 3. 0 = 4. 5 Ø Step 2: Plug variables into V = IR Ø 9 V = I (4. 5 ) Ø Solve for I: I = 2 A 8

Sample Question 0. 5 12. 0 25 V Find the current through the above circuit. 2 A 9

Parallel Circuits A branched pathway is formed for the flow of electrons through a circuit, connected to the terminals of a battery, generator, or wall socket. Ø A break in any path does not interrupt the flow of charge in the other paths. Ø A device in each branch operates independently of the others. Ø Total current in the branches adds. Ø

Resistors in Parallel have the same pressure difference across them. Ø When many resistors are connected in parallel, the sum of the current through each resistor equals the total current through the circuit. Ø To find the total current in a parallel circuit, find the current through each branch using V/R Ø Once you have the current in each branch, add them up to find the circuit current. Ø Ic = I 1 + I 2 + I 3…. . Ø 11

Equivalent Resistance - Parallel Ø The EQUIVALENT RESISTANCE of resistors in a parallel circuit can be calculated using a reciprocal relationship. Ø 1/Req = 1/R 1 + 1/R 2 + 1/R 3…. . 12

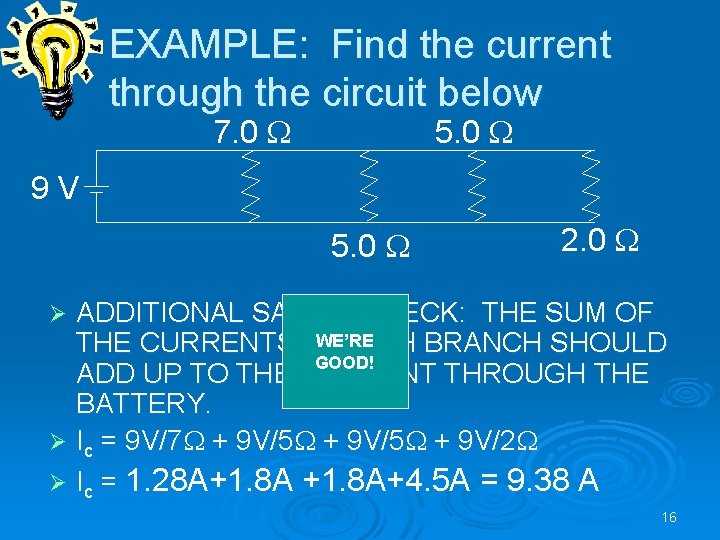
EXAMPLE: Find the current through the circuit below 7. 0 5. 0 9 V 5. 0 2. 0 Step 1: Find Equivalent Resistance Ø 1/Req = 1/7. 0 + 1/5. 0 + 1/2. 0 Ø 1/Req = 10/70 + 14/70 + 35/70 = 73/70 Ø Req = 70/73 = 0. 96 Ø 13

EXAMPLE: Find the current through the circuit below 7. 0 5. 0 9 V 5. 0 2. 0 Step 2: Substitute the Equivalent Resistance in to V = IR Ø 9 V = Ic (0. 96 ) Ø Solve for I: I = 9. 38 A Ø This is the current through the battery and the “trunk”. The current through each branch 14 depends on the resistance in the branch. Ø

EXAMPLE: Find the current through the circuit below 7. 0 5. 0 9 V 5. 0 2. 0 SANITY CHECK: THE EQUIVALENT RESISTANCE FOR RESISTORS IN PARALLEL IS LESS THAN THE SMALLEST INDIVIDUAL RESISTANCE. Ø 0. 96 < 2. 0 Ø 15

EXAMPLE: Find the current through the circuit below 7. 0 5. 0 9 V 5. 0 2. 0 ADDITIONAL SANITY CHECK: THE SUM OF WE’RE THE CURRENTS IN EACH BRANCH SHOULD GOOD! ADD UP TO THE CURRENT THROUGH THE BATTERY. Ø Ic = 9 V/7 + 9 V/5 + 9 V/2 Ø Ic = 1. 28 A+1. 8 A+4. 5 A = 9. 38 A Ø 16

SAMPLE QUESTION 10. 0 5. 0 9 V 10. 0 Find the current through the battery in the above circuit. 3. 6 A 17

18

Consider a lamp powered by a battery. Charge flows A. B. C. D. out of the battery and into the lamp. from the negative terminal to the positive terminal. with a slight time delay after the switch is closed. through both the battery and the lamp. 19

Which statement is correct? Voltage flows in a circuit. B. Charge flows in a circuit. C. Current causes voltage. D. All the above are correct. A. 20