Circuits and Analog Electronics Ch 4 Sinusoidal Steady

Circuits and Analog Electronics Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal 4. 2 Phasors 4. 3 Phasor Relationships for R, L and C 4. 4 Impedance 4. 5 Parallel and Series Resonance 4. 6 Examples for Sinusoidal Circuits Analysis 4. 7 Magnetically Coupled Circuits References: References Hayt-Ch 7; Gao-Ch 3;

Ch 4 Sinusoidal Steady State Analysis • Any steady state voltage or current in a linear circuit with a sinusoidal source is a sinusoid – All steady state voltages and currents have the same frequency as the source • In order to find a steady state voltage or current, all we need to know is its magnitude and its phase relative to the source (we already know its frequency) • We do not have to find this differential equation from the circuit, nor do we have to solve it • Instead, we use the concepts of phasors and complex impedances • Phasors and complex impedances convert problems involving differential equations into circuit analysis problems Focus on steady state; �� Focus on sinusoids.

Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal Key Words: Words Period: T , Frequency: f , Radian frequency Phase angle Amplitude: Vm Im

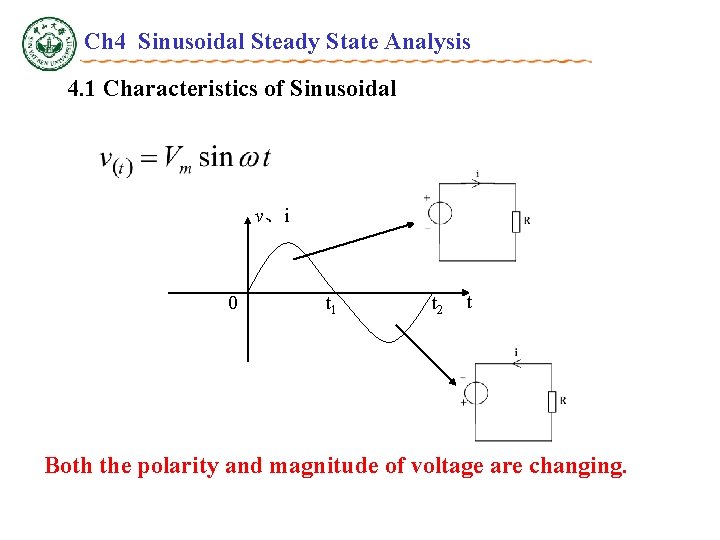
Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal v、i 0 t 1 t 2 t Both the polarity and magnitude of voltage are changing.

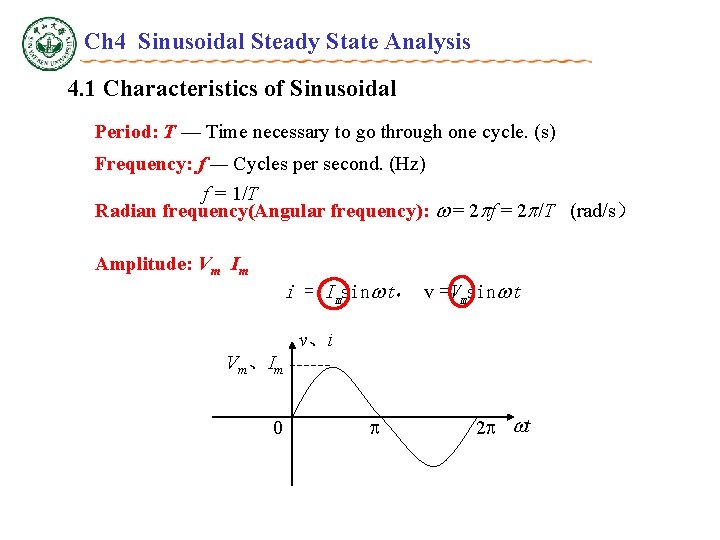
Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal Period: T — Time necessary to go through one cycle. (s) Frequency: f — Cycles per second. (Hz) f = 1/T Radian frequency(Angular frequency): = 2 f = 2 /T (rad/s） Amplitude: Vm Im i = Imsin t， v =Vmsin t v、i Vm、Im 0 2 t

Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal Effective Roof Mean Square (RMS) Value of a Periodic Waveform — is equal to the value of the direct current which is flowing through an R-ohm resistor. It delivers the same average power to the resistor as the periodic current does. Effective Value of a Periodic Waveform

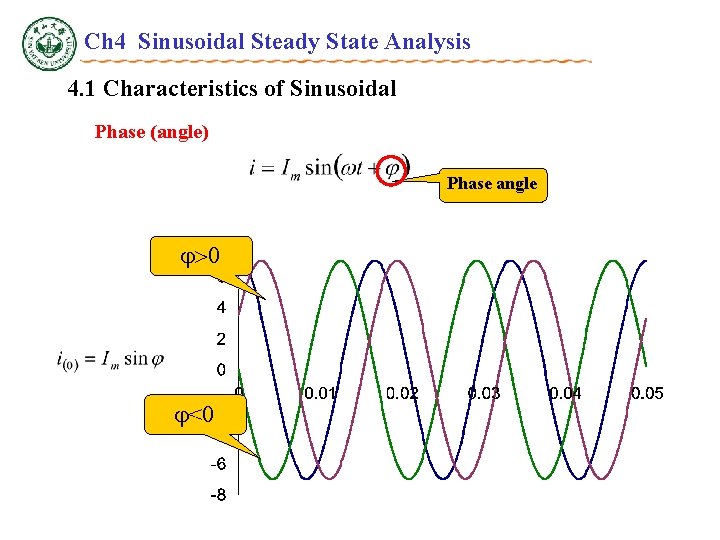
Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal Phase (angle) Phase angle 0 <0

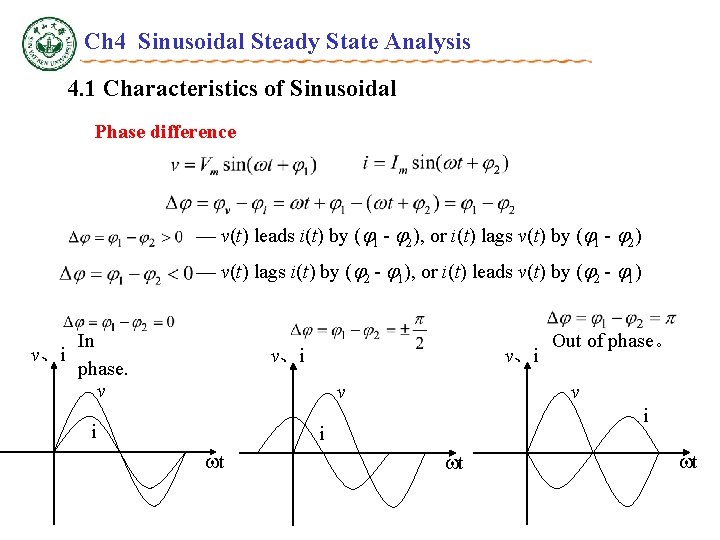
Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal Phase difference — v(t) leads i(t) by ( 1 - 2), or i(t) lags v(t) by ( 1 - 2) — v(t) lags i(t) by ( 2 - 1), or i(t) leads v(t) by ( 2 - 1) In v、i phase. v v、i v v i i i t Out of phase。 t t

Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal Review The sinusoidal means whose phases are compared must: ① Be written as sine waves or cosine waves. ② With positive amplitudes. ③ Have the same frequency. 360°—— does not change anything. 90° —— change between sin & cos. 180°—— change between + & -

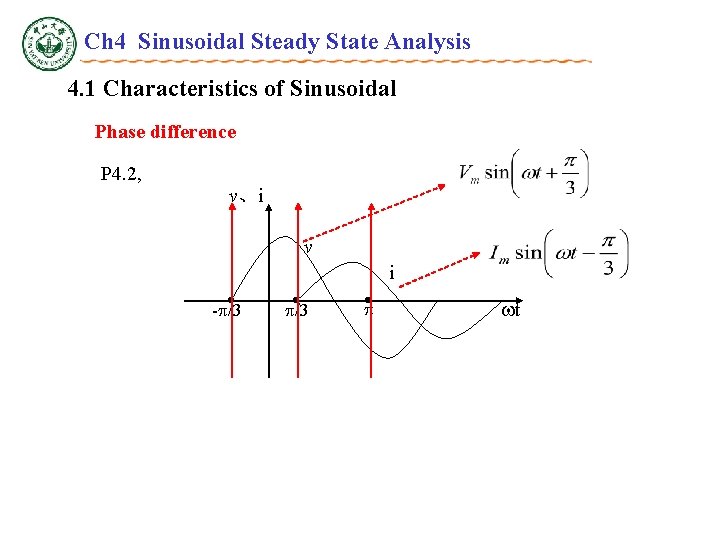
Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal Phase difference P 4. 1, Find

Ch 4 Sinusoidal Steady State Analysis 4. 1 Characteristics of Sinusoidal Phase difference P 4. 2, v、i v i • - /3 • t

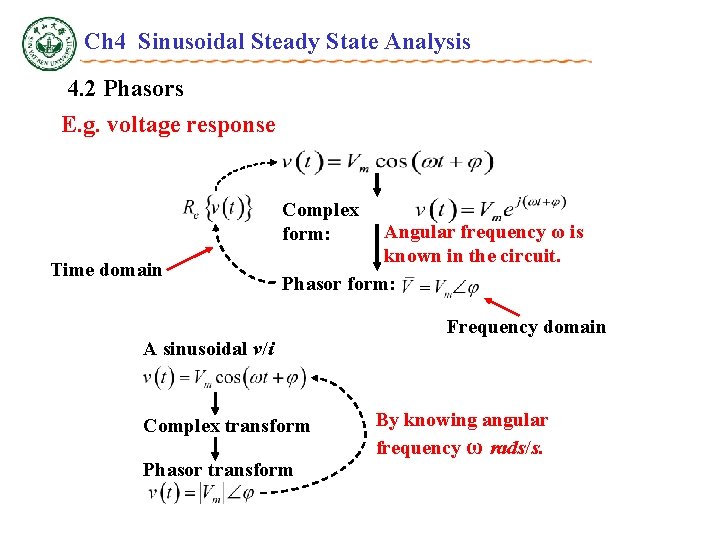
Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors A sinusoidal voltage/current at a given frequency , is characterized by only two parameters : amplitude an phase Key Words: Words Complex Numbers Rotating Vector Phasors

Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors E. g. voltage response Complex form: Time domain Angular frequency ω is known in the circuit. Phasor form: Frequency domain A sinusoidal v/i Complex transform Phasor transform By knowing angular frequency ω rads/s.

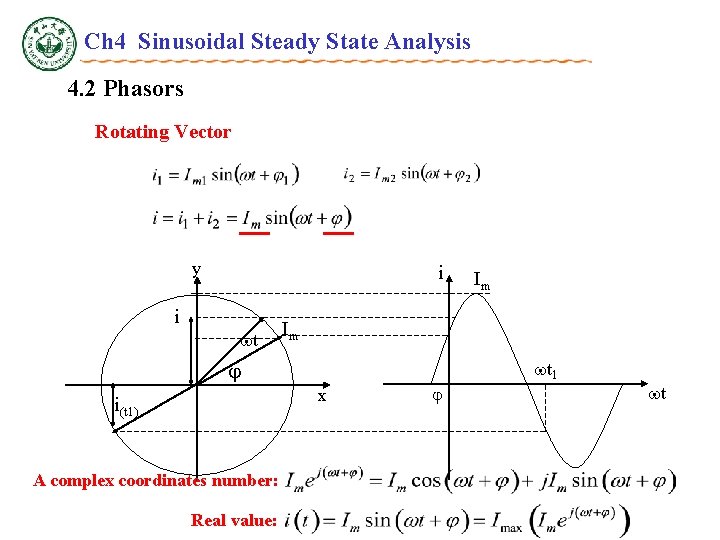
Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors Rotating Vector y i i t Im t 1 x i(t 1) A complex coordinates number: Real value: Im t

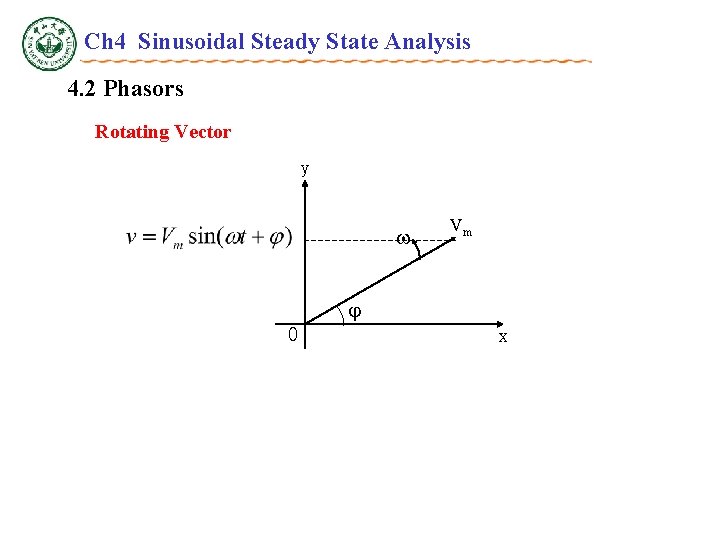
Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors Rotating Vector y Vm 0 x

Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors Complex Numbers — Rectangular Coordinates imaginary axis b |A | — Polar Coordinates real axis a conversion：

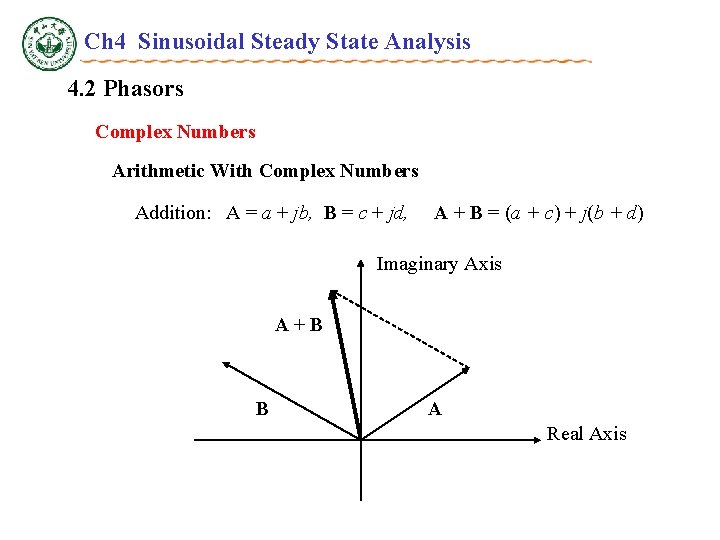
Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors Complex Numbers Arithmetic With Complex Numbers Addition: A = a + jb, B = c + jd, A + B = (a + c) + j(b + d) Imaginary Axis A + B B A Real Axis

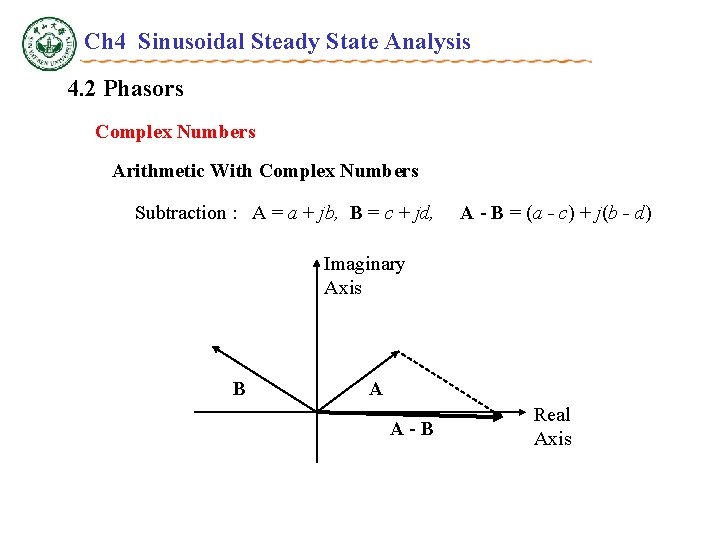
Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors Complex Numbers Arithmetic With Complex Numbers Subtraction : A = a + jb, B = c + jd, A - B = (a - c) + j(b - d) Imaginary Axis B A A - B Real Axis

Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors Complex Numbers Arithmetic With Complex Numbers Multiplication : A = Am A, B = Bm B A B = (Am Bm) ( A + B) Division: A = Am A , B = Bm B A / B = (Am / Bm) ( A - B) P 4. 3, Find：

Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors A phasor is a complex number that represents the magnitude and phase of a sinusoid: Phasor Diagrams • A phasor diagram is just a graph of several phasors on the complex plane (using real and imaginary axes). • A phasor diagram helps to visualize the relationships between currents and voltages.

Ch 4 Sinusoidal Steady State Analysis 4. 2 Phasors Complex Exponentials l A real-valued sinusoid is the real part of a complex exponential. l Complex exponentials make solving for AC steady state an algebraic problem.

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Key Words: Words I-V Relationship for R, L and C, Power conversion

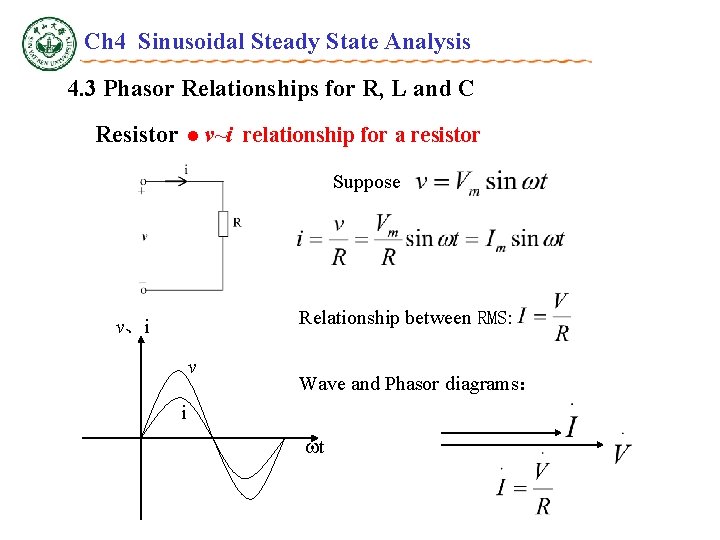
Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Resistor l v~i relationship for a resistor Suppose Relationship between RMS: v、i v Wave and Phasor diagrams： i t

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Resistor l Time domain frequency domain With a resistor θ� φ, v(t) and i(t) are in phase.

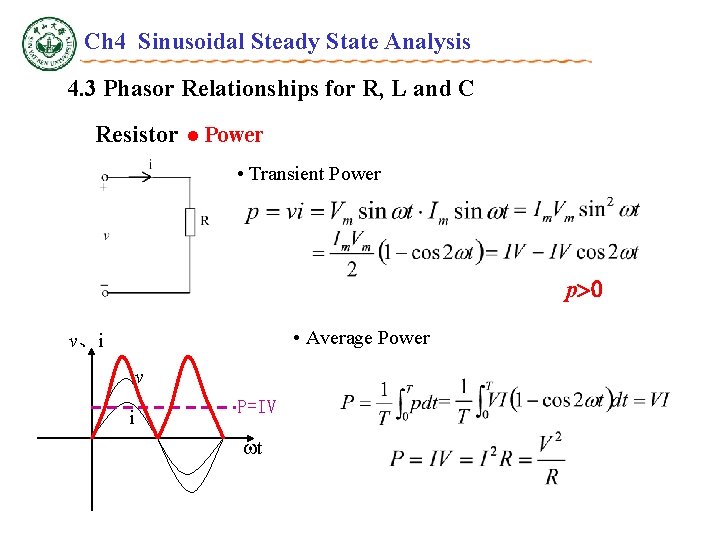
Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Resistor l Power • Transient Power p 0 • Average Power v、i v i P=IV t

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Resistor P 4. 4 ， , R=10 ，Find i and P。

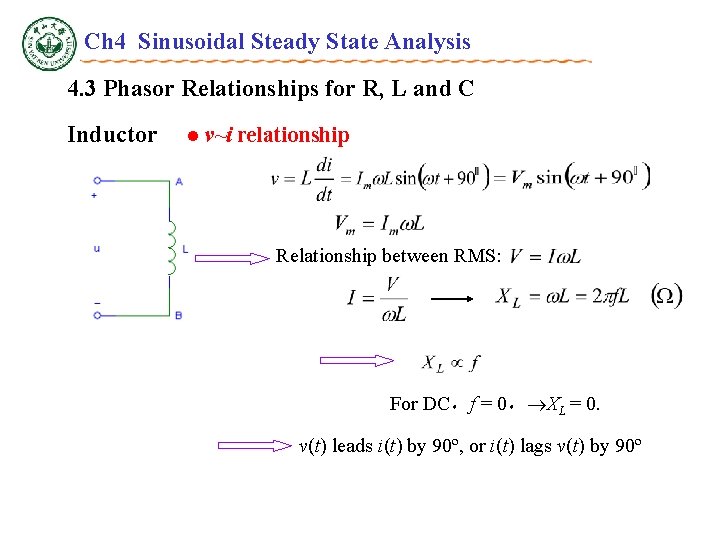
Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Inductor l v~i relationship Suppose

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Inductor l v~i relationship Relationship between RMS: For DC，f = 0， XL = 0. v(t) leads i(t) by 90º, or i(t) lags v(t) by 90º

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Inductor l v ~ i relationship i(t) = Im ej t Represent v(t) and i(t) as phasors: • The derivative in the relationship between v(t) and i(t) becomes a multiplication by j in the relationship between V and I. • The time-domain differential equation has become the algebraic equation in the frequency-domain. • Phasors allow us to express current-voltage relationships for inductors and capacitors in a way such as we express the current-voltage relationship for a resistor.

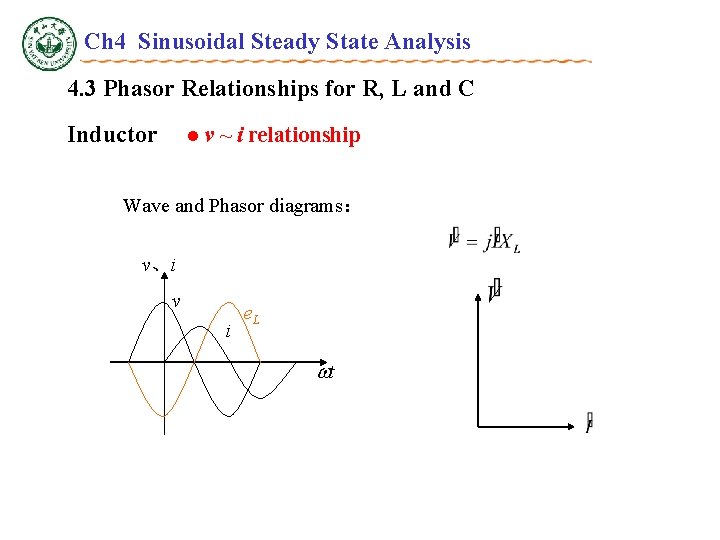
Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Inductor l v ~ i relationship Wave and Phasor diagrams： v、i v i e. L t

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Inductor l Power P Energy stored: + + - - t v、i Average Power v Reactive Power （Var） i t

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Inductor P 4. 5，L = 10 m. H，v = 100 sin t，Find i. L when f = 50 Hz and 50 k. Hz.

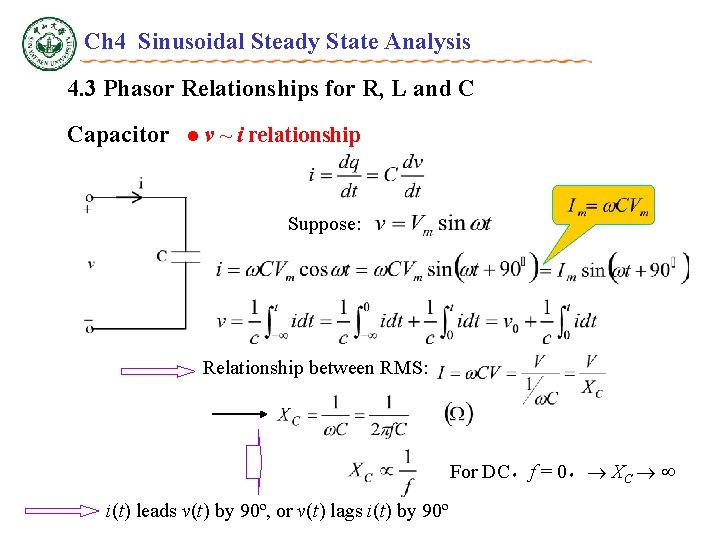
Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Capacitor l v ~ i relationship Suppose: Relationship between RMS: For DC，f = 0， XC i(t) leads v(t) by 90º, or v(t) lags i(t) by 90º

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Capacitor l v ~ i relationship v(t) = Vm ej t Represent v(t) and i(t) as phasors: • The derivative in the relationship between v(t) and i(t) becomes a multiplication by j in the relationship between V and I. • The time-domain differential equation has become the algebraic equation in the frequency-domain. • Phasors allow us to express current-voltage relationships for inductors and capacitors much like we express the current-voltage relationship for a resistor.

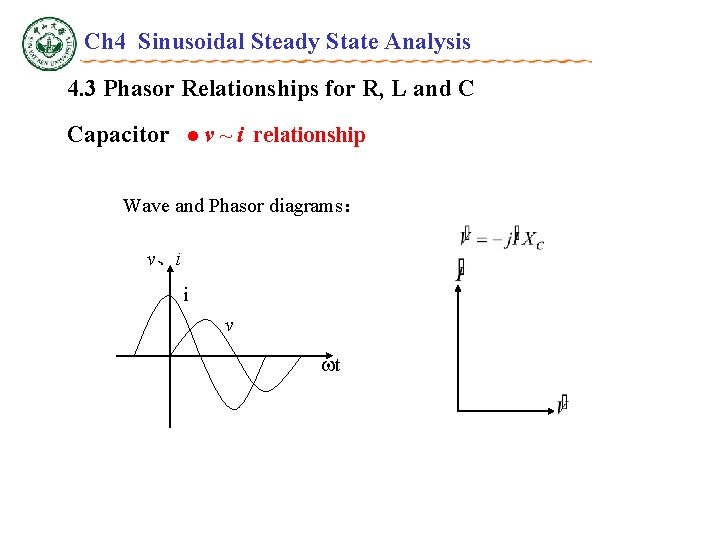
Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Capacitor l v ~ i relationship Wave and Phasor diagrams： v、i i v t

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Capacitor l. Power P Energy stored: + + - - t v、i Average Power: P=0 i Reactive Power （Var） v t

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Capacitor P 4. 7，Suppose C=20 F，AC source v=100 sin t，Find XC and I for f = 50 Hz, 50 k. Hz。

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Review (v-I relationship) Time domain Frequency domain , v and i are in phase. R L C , , v leads i by 90°. , , v lags i by 90°.

Ch 4 Sinusoidal Steady State Analysis 4. 3 Phasor Relationships for R, L and C Summary l R： L： C： l Frequency characteristics of an Ideal Inductor and Capacitor: A capacitor is an open circuit to DC currents; A Inducter is a short circuit to DC currents. l

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Key Words: Words complex currents and voltages. Impedance Phasor Diagrams

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Complex voltage， Complex current， Complex Impedance • AC steady-state analysis using phasors allows us to express the relationship between current and voltage using a formula that looks likes Ohm’s law: Z is called impedance. measured in ohms ( )

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Complex Impedance • Complex impedance describes the relationship between the voltage across an element (expressed as a phasor) and the current through the element (expressed as a phasor) • Impedance is a complex number and is not a phasor (why? ). • Impedance depends on frequency

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Complex Impedance Resistor——The impedance is R ZR = R = 0（ ＝ 0); or ZR = R 0 Capacitor——The impedance is 1/j C or =- /2 Inductor——The impedance is j L or = /2

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Complex Impedance in series/parallel can be combined as resistors. Voltage divider: Current divider:

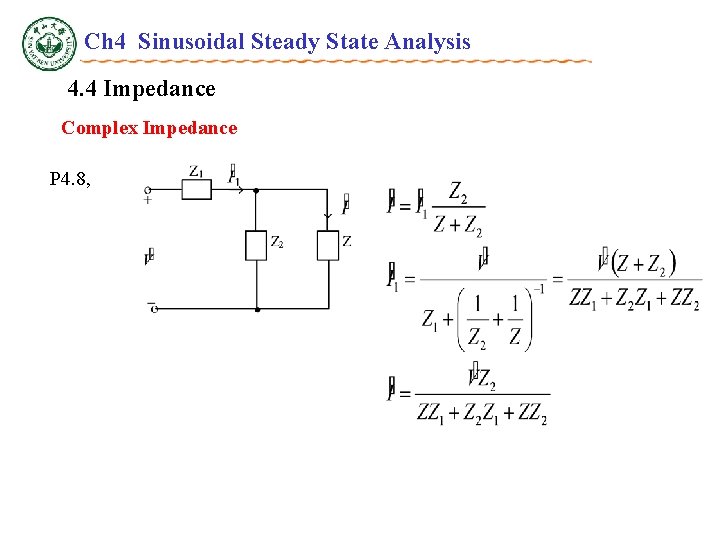
Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Complex Impedance P 4. 8,

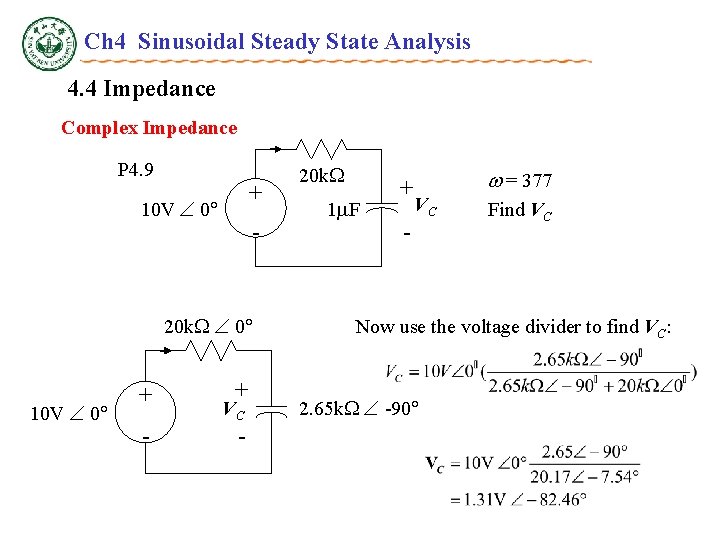
Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Complex Impedance Phasors and complex impedance allow us to use Ohm’s law with complex numbers to compute current from voltage and voltage from current P 4. 9 10 V 0 + - 20 k 1 F + - VC = 377 Find VC • How do we find VC? • First compute impedances for resistor and capacitor: ZR = 20 k 0 ZC = 1/j (377 *1 F) = 2. 65 k -90

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Complex Impedance P 4. 9 + 10 V 0 - 20 k 0 10 V 0 + - + VC - 20 k 1 F + - = 377 VC Find VC Now use the voltage divider to find VC: 2. 65 k -90

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Complex Impedance allows us to use the same solution techniques for AC steady state as we use for DC steady state. • All the analysis techniques we have learned for the linear circuits are applicable to compute phasors – KCL & KVL – node analysis / loop analysis – superposition – Thevenin equivalents / Norton equivalents – source exchange • The only difference is that now complex numbers are used.

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Kirchhoff’s Laws KCL and KVL hold as well in phasor domain. KCL: KVL： ik- Transient current of the #k branch vk- Transient voltage of the #k branch

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Admittance • I = YV, Y is called admittance, the reciprocal of impedance, measured in siemens (S) • Resistor: – The admittance is 1/R • Inductor: – The admittance is 1/j L • Capacitor: – The admittance is j C

Ch 4 Sinusoidal Steady State Analysis 4. 4 Impedance Phasor Diagrams • A phasor diagram is just a graph of several phasors on the complex plane (using real and imaginary axes). • A phasor diagram helps to visualize the relationships between currents and voltages. I = 2 m. A 40 , VR = 2 V 40 VC = 5. 31 V -50 , V = 5. 67 V -29. 37 2 m. A 40 + 1 F V 1 k – + VC – + – Imaginary Axis VR VR Real Axis V VC

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Key Words: Words RLC Circuit, Series Resonance Parallel Resonance

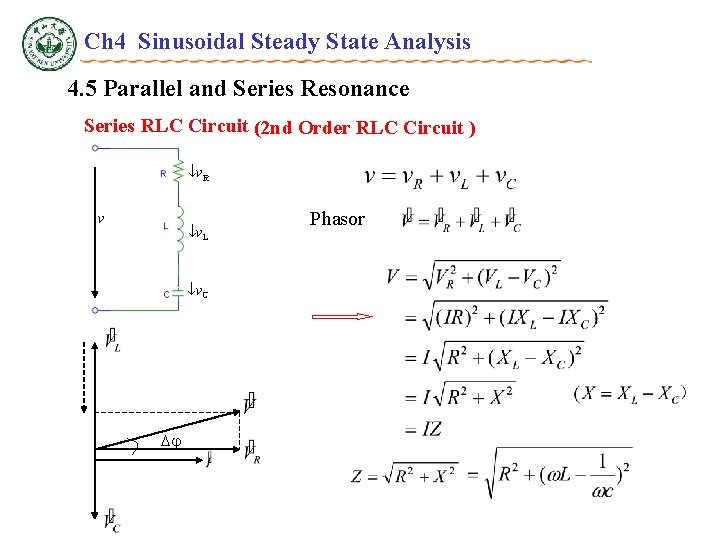
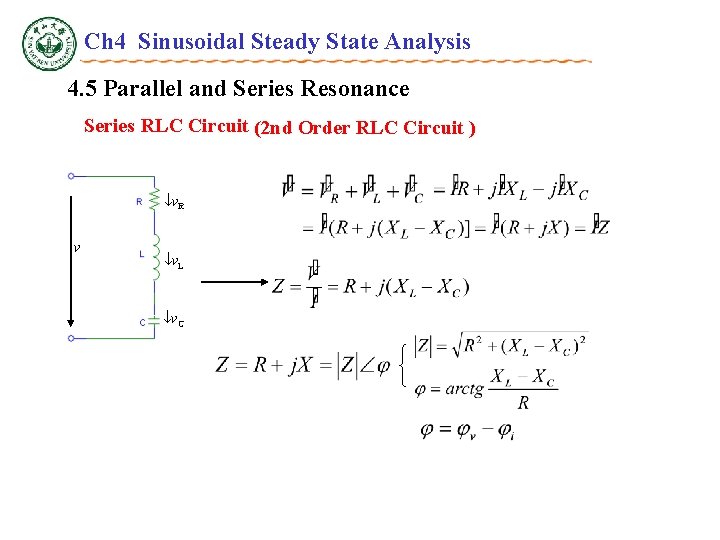
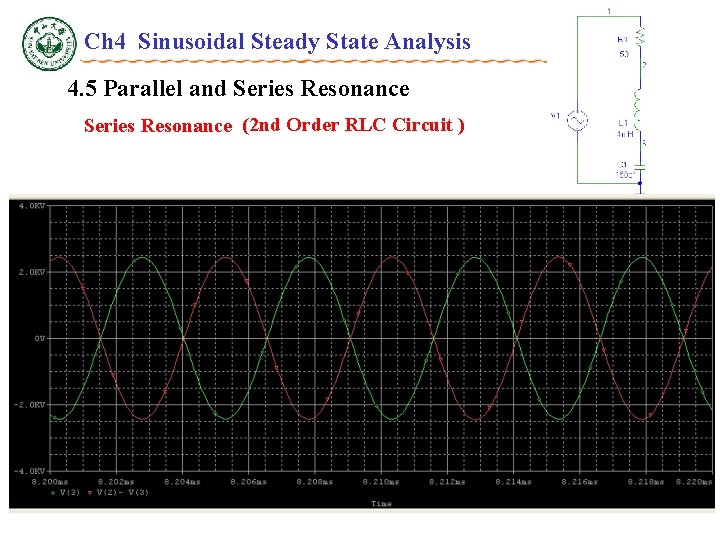
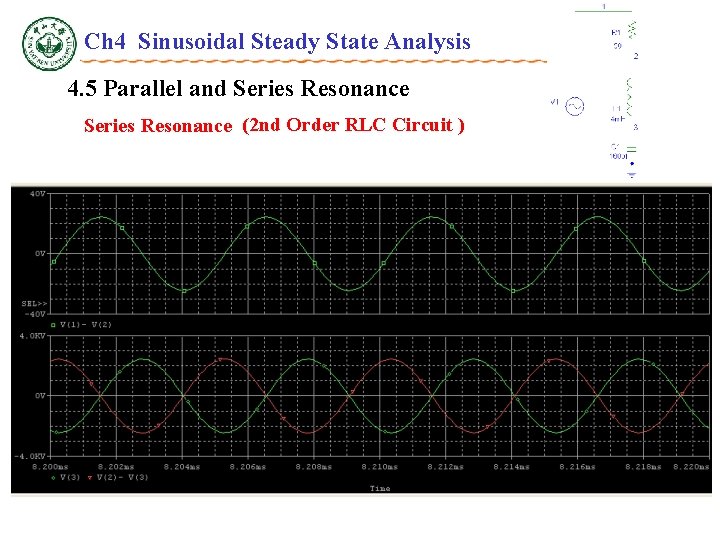
Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Series RLC Circuit (2 nd Order RLC Circuit ) v. R v v. L v. C Phasor

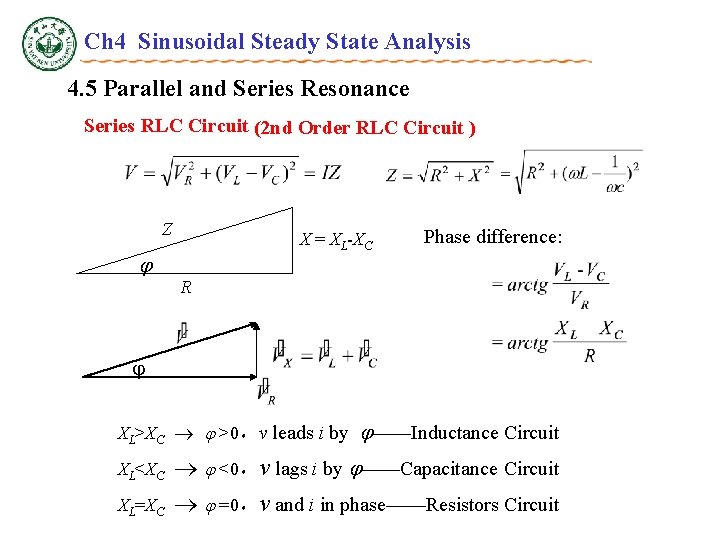
Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Series RLC Circuit (2 nd Order RLC Circuit ) Z X = XL-XC Phase difference: R XL>XC >0，v leads i by ——Inductance Circuit XL<XC XL=XC <0，v lags i by ——Capacitance Circuit =0，v and i in phase——Resistors Circuit

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Series RLC Circuit (2 nd Order RLC Circuit ) v. R v v. L v. C

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Series RLC Circuit (2 nd Order RLC Circuit ) P 4. 9, R. L. C Series Circuit，R = 30 ，L = 127 m. H，C = 40 F，Source , Find 1) XL、XC、Z； 2) I and i； 3) VR and v. R； VL and v. L； VC and v. C； 4) Phasor Diagrams v. R v v. L v. C P 4. 10，Computing by (complex numbers) Phasors

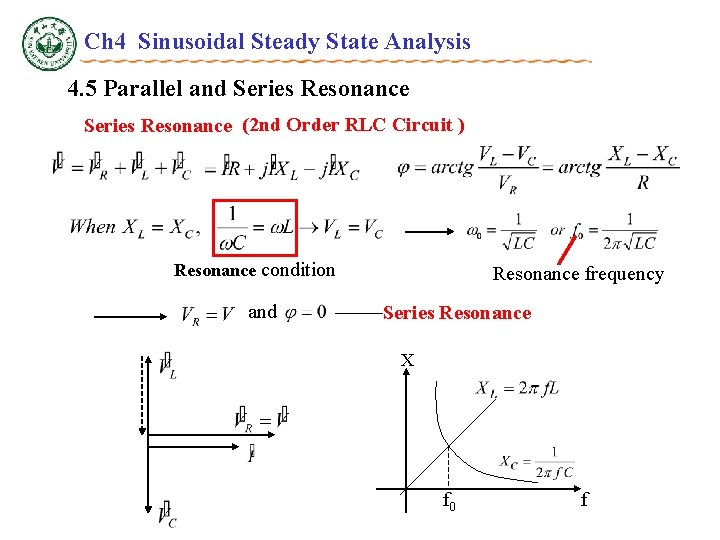
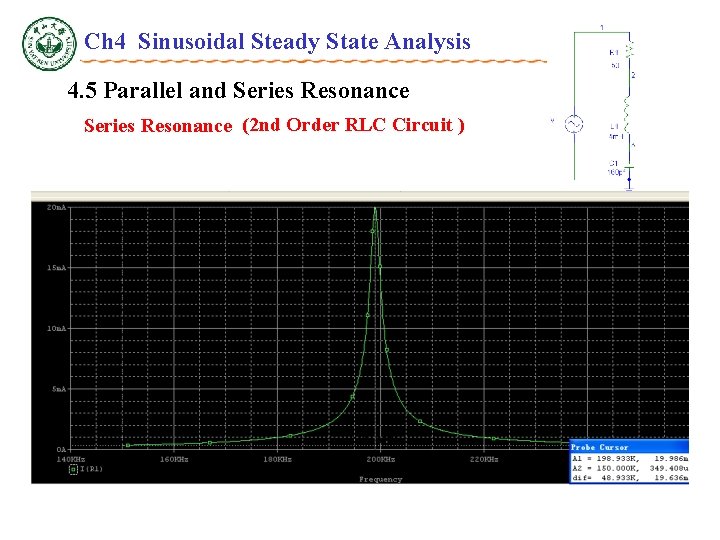
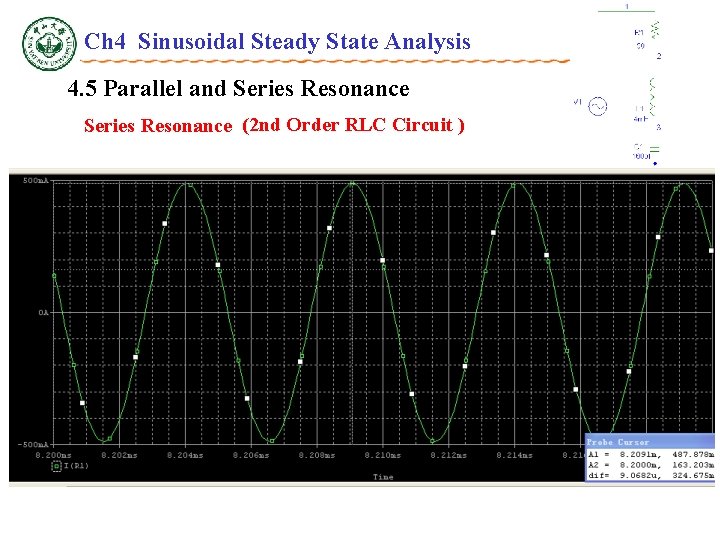
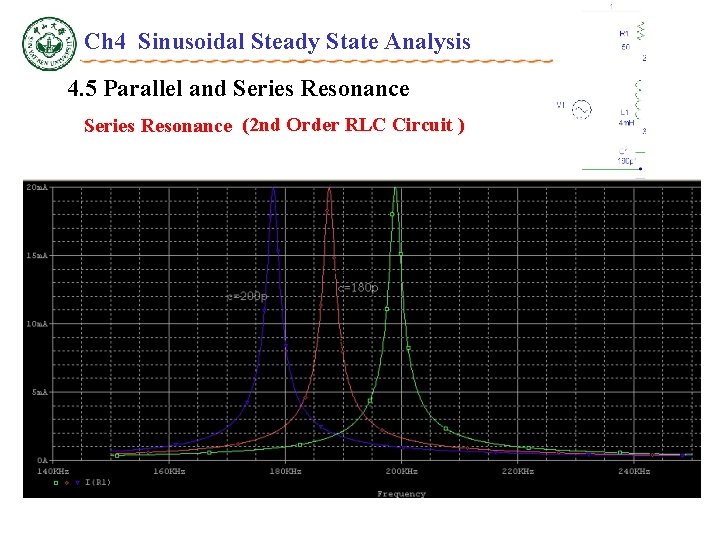
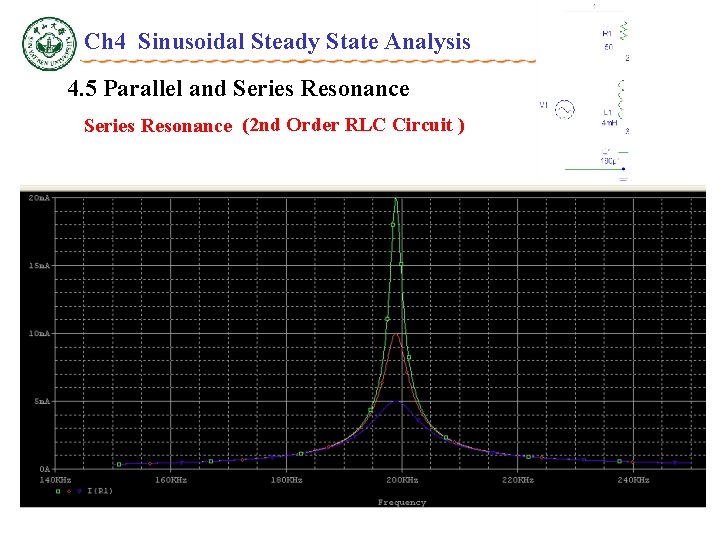
Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance (2 nd Order RLC Circuit ) Resonance condition and Resonance frequency ——Series Resonance X f 0 f

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance (2 nd Order RLC Circuit ) Resonance condition: • Zmin；when V=constant, I=Imax=I 0。 • When , • Quality factor Q,

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance (2 nd Order RLC Circuit )

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance (2 nd Order RLC Circuit )

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance (2 nd Order RLC Circuit )

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance (2 nd Order RLC Circuit )

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance (2 nd Order RLC Circuit )

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance (2 nd Order RLC Circuit )

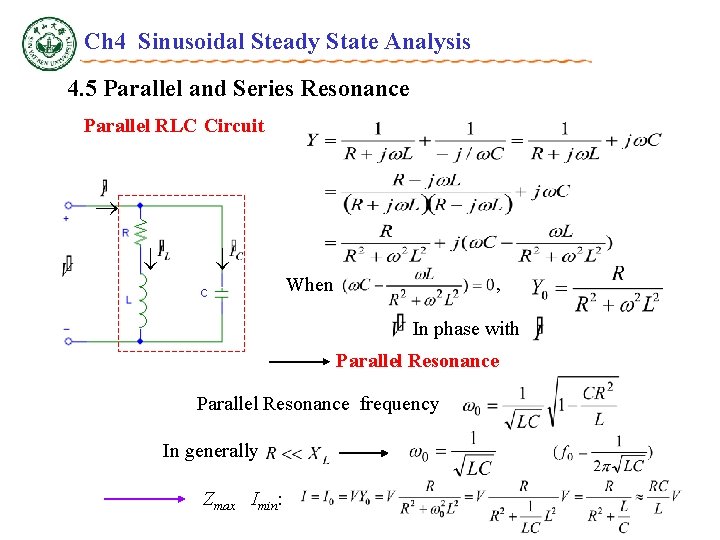
Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Parallel RLC Circuit , When In phase with Parallel Resonance frequency In generally Zmax Imin:

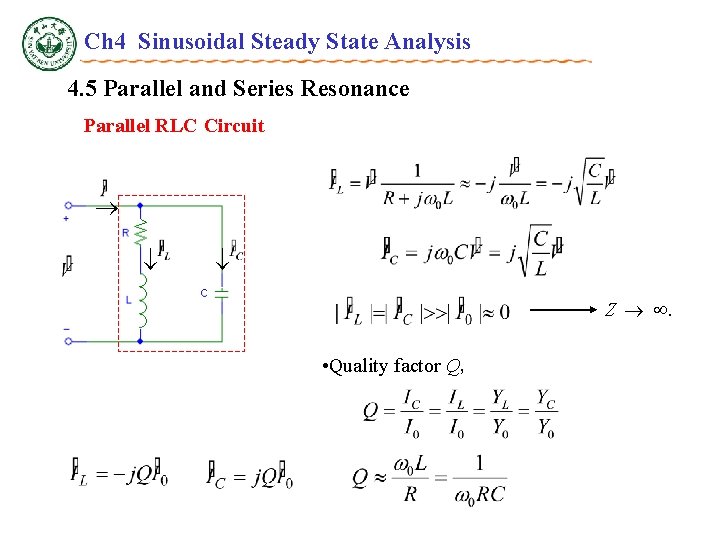
Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Parallel RLC Circuit Z . • Quality factor Q,

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Parallel RLC Circuit P 4. 10, i v i 1 Find i 1、 i 2、 i i 2

Ch 4 Sinusoidal Steady State Analysis 4. 5 Parallel and Series Resonance Parallel RLC Circuit Review For sinusoidal circuit， Series ： Parallel : Two Simple Methods: Phasor Diagrams and Complex Numbers ？

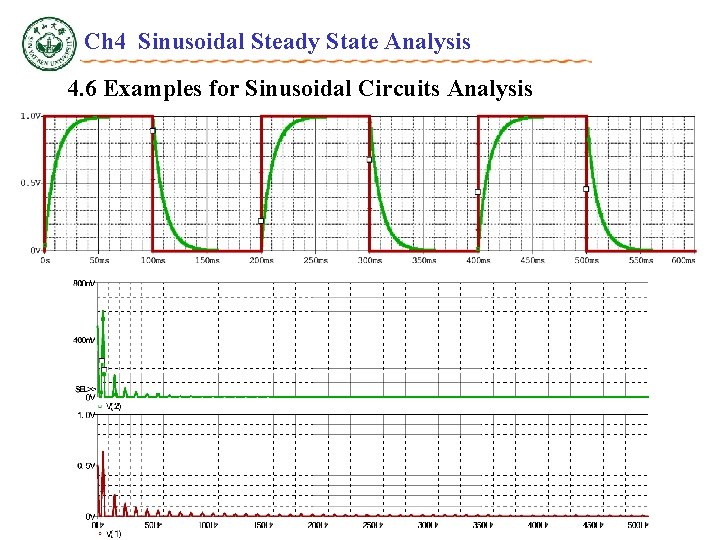
Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis Key Words: Words Bypass Capacitor RC Phase Difference Low-Pass and High-Pass Filter

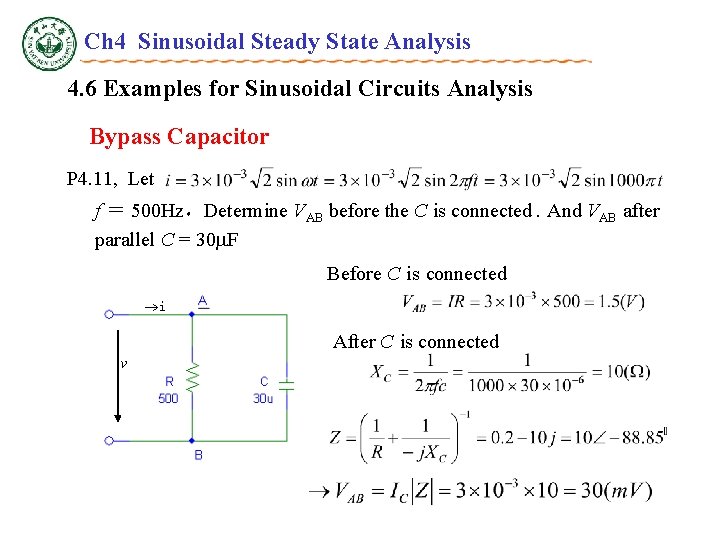
Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis Bypass Capacitor P 4. 11, Let f ＝ 500 Hz，Determine VAB before the C is connected. And VAB after parallel C = 30 F Before C is connected i After C is connected v

Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis RC Phase Difference P 4. 12, f = 300 Hz, R = 100 。 If vo - vi= /4，C =？

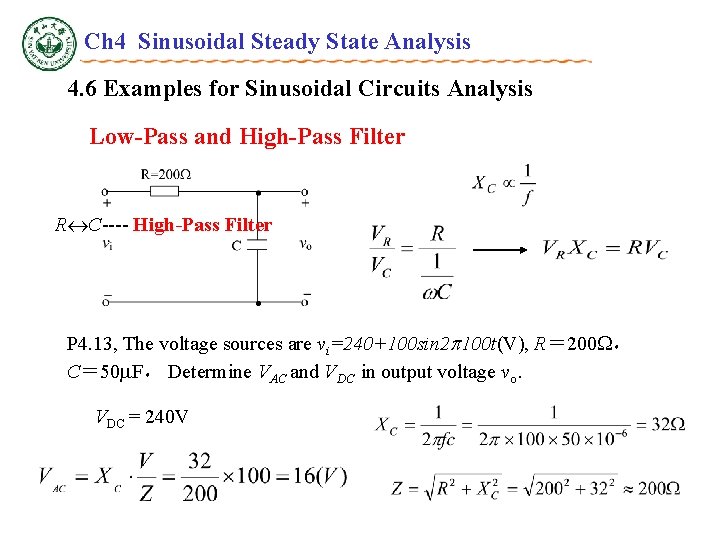
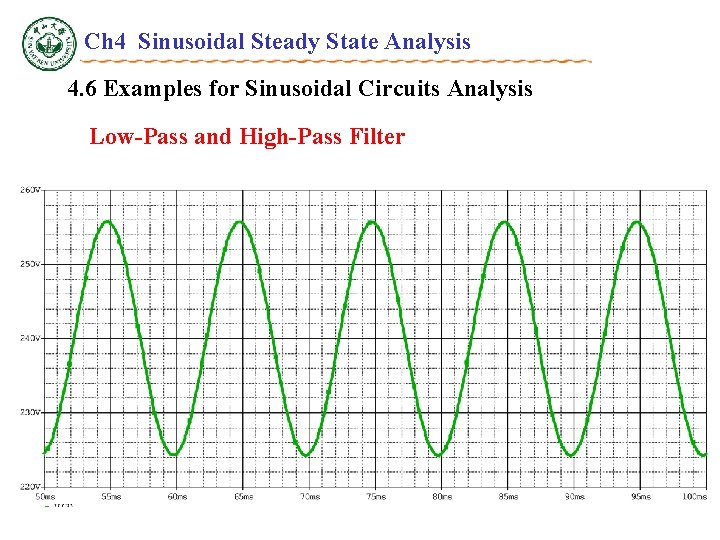
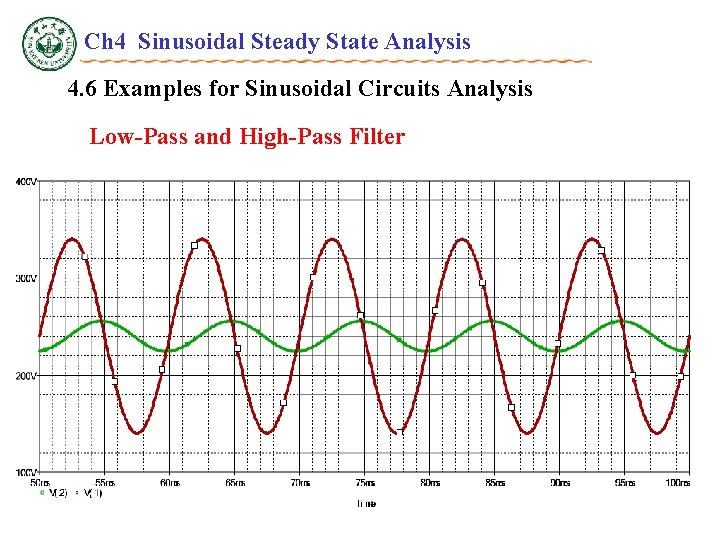
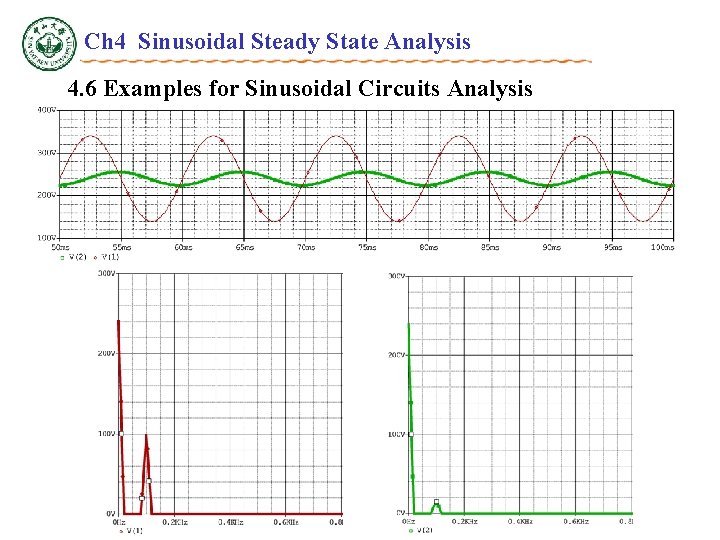
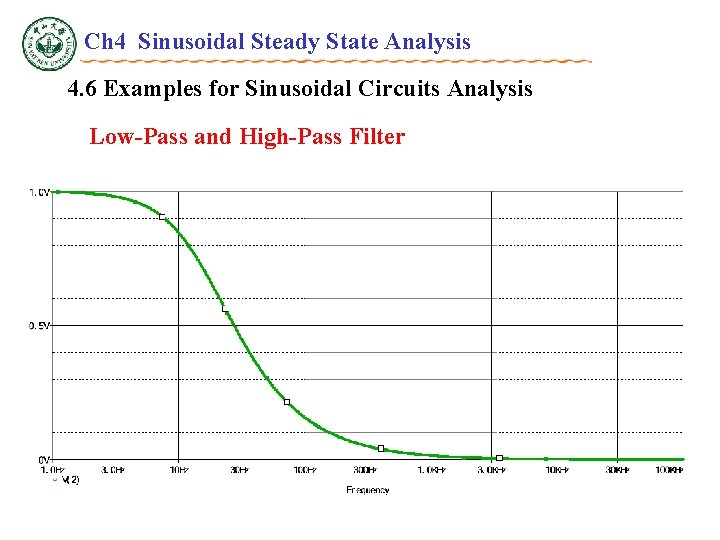
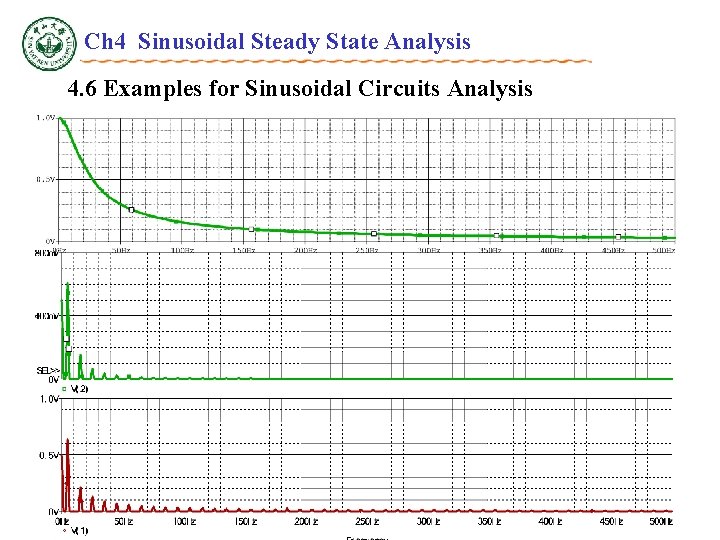
Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis Low-Pass and High-Pass Filter R C---- High-Pass Filter P 4. 13, The voltage sources are vi=240+100 sin 2 100 t(V), R＝ 200 ， C＝ 50 F， Determine VAC and VDC in output voltage vo. VDC = 240 V

Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis Low-Pass and High-Pass Filter

Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis Low-Pass and High-Pass Filter

Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis

Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis Low-Pass and High-Pass Filter

Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis

Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis

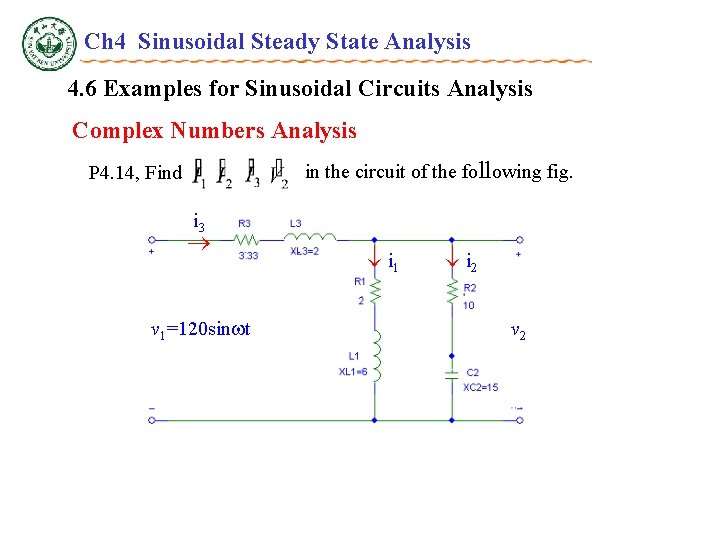
Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis Complex Numbers Analysis in the circuit of the following fig. P 4. 14, Find i 3 v 1=120 sin t i 1 i 2 v 2

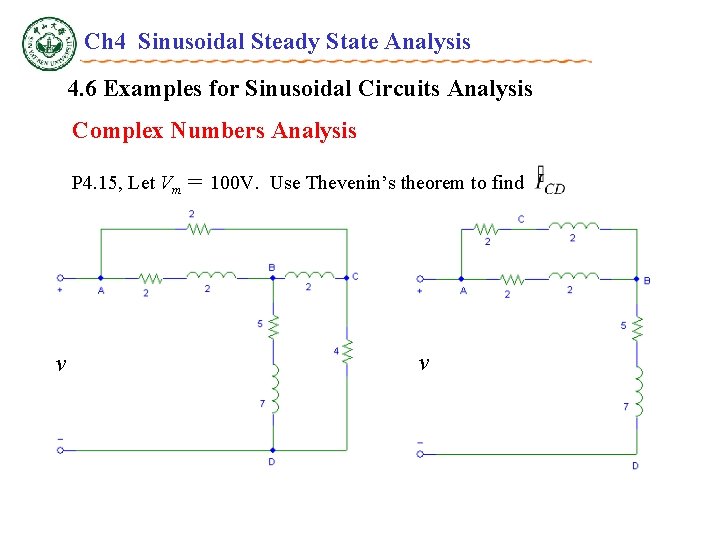
Ch 4 Sinusoidal Steady State Analysis 4. 6 Examples for Sinusoidal Circuits Analysis Complex Numbers Analysis P 4. 15, Let Vm ＝ 100 V. Use Thevenin’s theorem to find v v

Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits Key Words: Words Self- inductance and Mutual inductance Magnetically Coupled Circuits and v ~ i relationship Dot convention Ideal transformer

Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits and v~i relationship Magnetic flux: 1 ＝ f(i 1) ( 1 = N 1 1) The flux is proportional to the current in linear inductor: 1(t) ＝ L 1 i 1(t) L is a lumped element abstraction for the coil. i 1 + v 1 - i 1 v 1 Voltage be proportional to the time rate of change of the magnetic field.

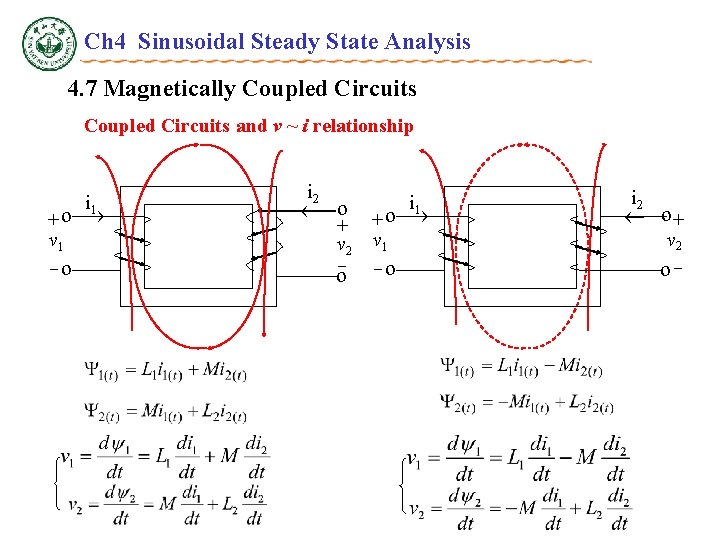
Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits and v~i relationship i 2 + v 2 - i 1 + v 1 - ——Ideal Coupled Circuits’ v ~ i relationship l L 1、L 2、M represent Ideal Coupled Inductor l Self- inductance voltage Mutual- inductance voltage

Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits and v ~ i relationship + v 1 - i 2 + v 2 - + i 1 v 1 - i 2 + v 2 -

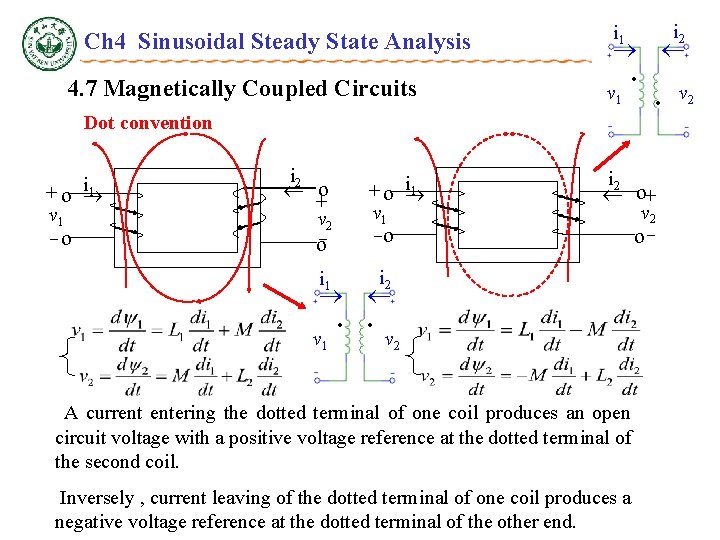
Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits + + v 1 - i 2 + v 2 - v 1 - i 1 v 1 i 1 • v 1 • • i 2 + v 2 - i 2 • Dot convention i 1 i 2 i 1 v 2 A current entering the dotted terminal of one coil produces an open circuit voltage with a positive voltage reference at the dotted terminal of the second coil. Inversely , current leaving of the dotted terminal of one coil produces a negative voltage reference at the dotted terminal of the other end. v 2

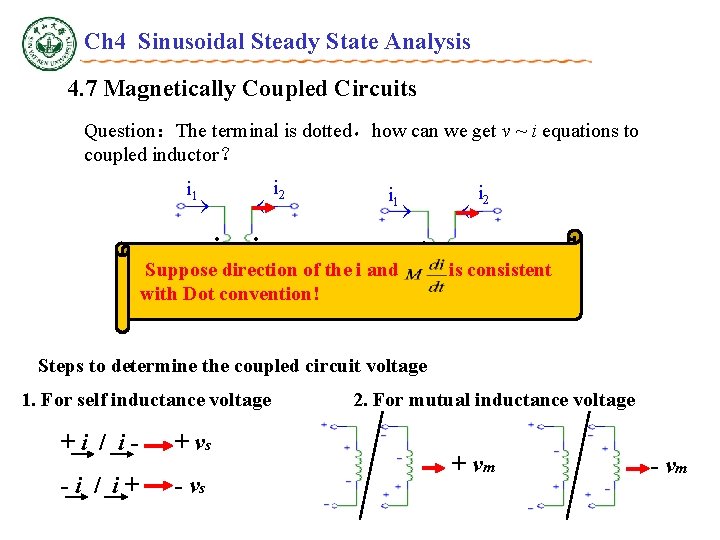
Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits Question：The terminal is dotted，how can we get v ~ i equations to coupled inductor？ i 2 i 1 • • i 2 i 1 v 1 v 2 v 1 u 2 of the i and Suppose direction with Dot convention! • v 2 is • consistent Steps to determine the coupled circuit voltage 1. For self inductance voltage +i / i- + vs -i / i+ - vs 2. For mutual inductance voltage + vm - vm

Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits P 4. 16，For the circuit shown in following figures, determine v 1 and v 2. i 1 v 1 • L 1 M i 1 i 2 • uv 2 L 2 2 v 1 • L 1 M i 2 i 1 L 2 • uv 2 2 v 1 L 1 • M i 2 － • L 2 u 2 v 2 ＋

Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits and v ~ i relationship i 1 + v 1 - i 2 + v 2 ——Ideal Coupled Circuits’s v~i relationship For sinusoidal circuit,

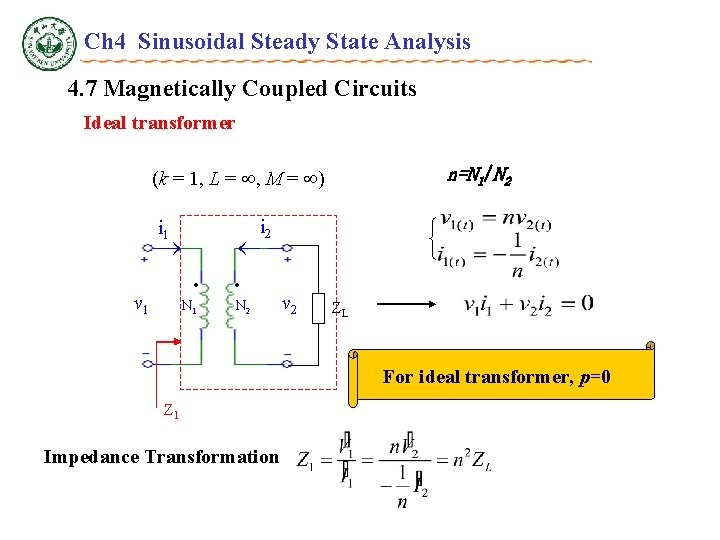
Ch 4 Sinusoidal Steady State Analysis 4. 7 Magnetically Coupled Circuits Ideal transformer n=N 1/N 2 (k = 1, L = , M = ) i 2 i 1 • v 1 N 1 • N 2 u 2 v 2 ZL For ideal transformer, p=0 Z 1 Impedance Transformation