Circuit Simulation via Matrix Exponential Operators CK Cheng

Outline • General Matrix Exponential • Krylov Space and Arnoldi Orthogonalization • Matrix Exponential

Krylov Space and Arnoldi Orthonormalization Input A and v 1=x 0/|x 0| Output AV=VH+hm+1

Standard Krylov Space Generate: AV=VH+hm+1 vm+1 em. T Thus, we have e. Ahv 1≈Ve.

Standard Mexp Error trend sweep m and h 6

Invert Krylov Space Generate: A-1 V=VH+hm+1 vm+1 em. T Let H=H-1, we have e.

Invert Matrix Exponential • large step size with less dimension sweep m and h

Rational Krylov Space Generate: (1 -r. A)-1 V=VH+hm+1 vm+1 em. T Let H=1/r (I-H-1)

Rational Matrix Exponential • large step size with less dimension fix , sweep m

Spectral Transformation – = 10 f • • • Small RC mesh, 100 by

Spectral Transformation– = 1 p • • • Small RC mesh, 100 by 100

Spectral Transformation– = 100 p • • • Small RC mesh, 100 by 100

Difference Between Inverted and Rational 18

Krylov Space Residual Generate: AV=VH+hm+1 vm+1 em. T Thus, we have e. Ahv 1≈Ve.

Krylov Space Residual • 1 ��. 1 m-1 �� 1 1 ��. 2 m-1

Slides: 28

Download presentation

Circuit Simulation via Matrix Exponential Operators CK Cheng UC San Diego 1

Outline • General Matrix Exponential • Krylov Space and Arnoldi Orthogonalization • Matrix Exponential Method – Krylov Subspace Approximation – Invert Krylov Subspace Approximation – Rational Krylov Subspace Approximation 2

General Matrix Exponential • 3

Krylov Space and Arnoldi Orthonormalization Input A and v 1=x 0/|x 0| Output AV=VH+hm+1 vm+1 em. T For i=1, …, m • Ti+1=Avi • For j=1, …, I – hji=<Ti+1, vj> – Ti+1=Ti+1 -hjivj • End For • hi+1, i=|Ti+1| • vi+1=1/hi+1 Ti+1 End For 4

Standard Krylov Space Generate: AV=VH+hm+1 vm+1 em. T Thus, we have e. Ahv 1≈Ve. Hhe 1 Residual r=Cdx/dt-Gx=-hm+1 Cvm+1 em. Te. Hhe 1 Derivation: Cdx/dt-Gx=CVHe. Hhe 1 -GVe. Hhe 1 =(CVH-GV)e. Hhe 1 = C(VH-C-1 GV)e. Hhe 1 =C(VH-VH-hm+1 vm+1 em. T)e. Hhe 1 =-hm+1 Cvm+1 em. Te. Hhe 1 5

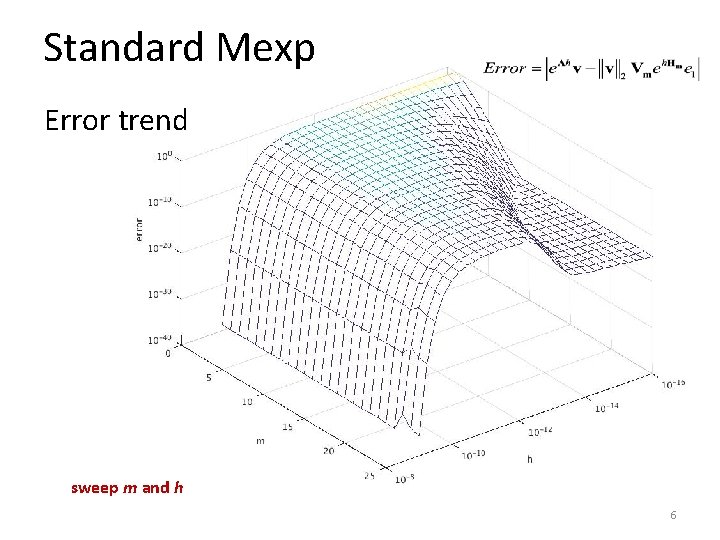
Standard Mexp Error trend sweep m and h 6

Invert Krylov Space Generate: A-1 V=VH+hm+1 vm+1 em. T Let H=H-1, we have e. Ahv 1≈Ve. Hhe 1 Residual r=Cdx/dt-Gx=hm+1 Gvm+1 em. THe. Hhe 1 Derivation: Cdx/dt-Gx=CVHe. Hhe 1 -GVe. Hhe 1 =(CVH-GV)e. Hhe 1 = G(G-1 CVH-V)e. Hhe 1 =G(A-1 VH-V)e. Hhe 1 =hm+1 Gvm+1 em. THe. Hhe 1 7

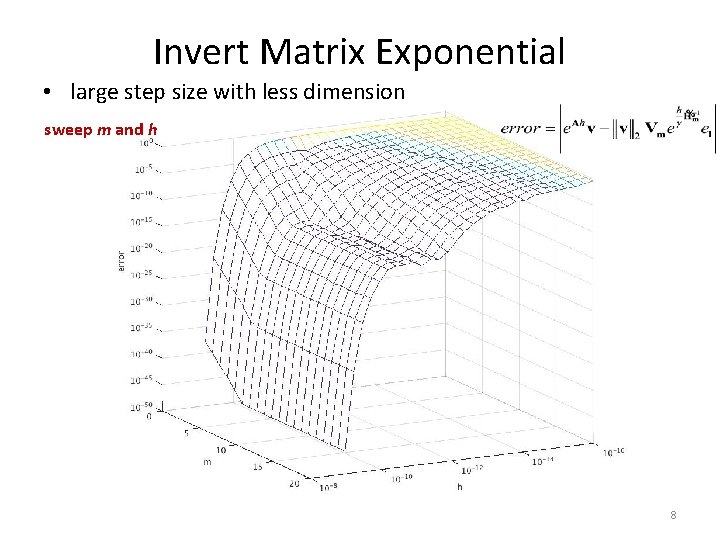
Invert Matrix Exponential • large step size with less dimension sweep m and h 8

Rational Krylov Space Generate: (1 -r. A)-1 V=VH+hm+1 vm+1 em. T Let H=1/r (I-H-1) we have e. Ahv 1≈Ve. Hhe 1 Residual r=Cdx/dt-Gx=-hm+1(C/r-G)vm+1 em. TH-1 e. Hhe 1 Derivation: Cdx/dt-Gx=CVHe. Hhe 1 -GVe. Hhe 1 =(CVH-GV)e. Hhe 1 = (1/r CV(I-H-1)-GV)e. Hhe 1 =(1/r. CV(H-1)-GVH)H-1 e. Hhe 1 =((1/r. C-G)VH-1/r. CV)H-1 e. Hhe 1 =-hm+1(C/r-G)vm+1 em. TH-1 e. Hhe 1 9

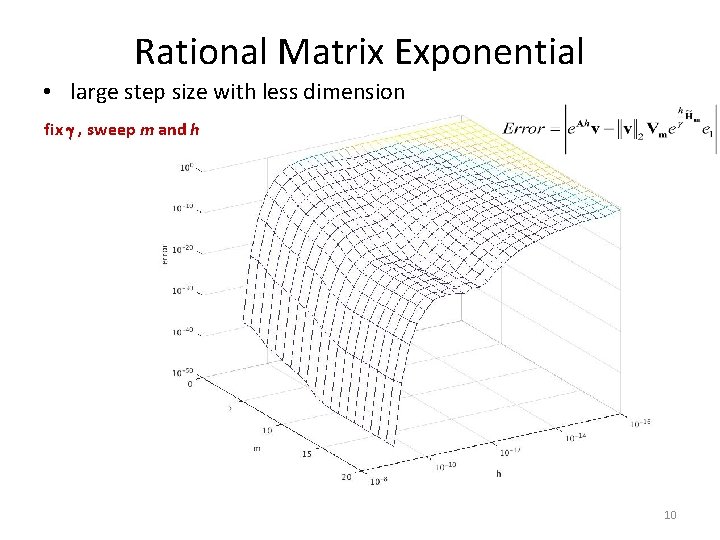
Rational Matrix Exponential • large step size with less dimension fix , sweep m and h 10

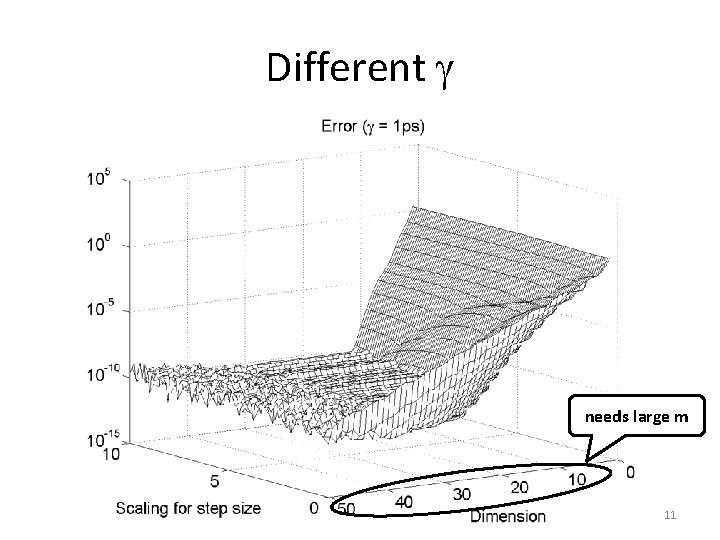
Different needs large m 11

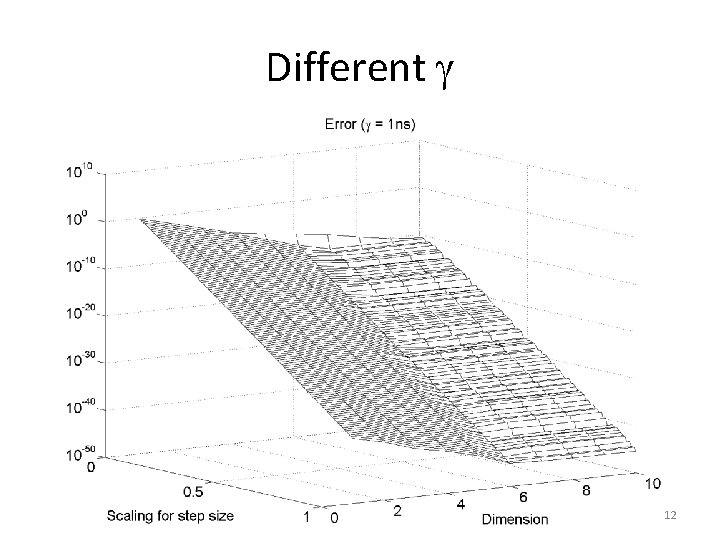
Different 12

Spectral Transformation – = 10 f • • • Small RC mesh, 100 by 100 Different h for Krylov subspace Different for rational Krylov subspace 13

Spectral Transformation– = 1 p • • • Small RC mesh, 100 by 100 Different h for Krylov subspace Different for rational Krylov subspace 14

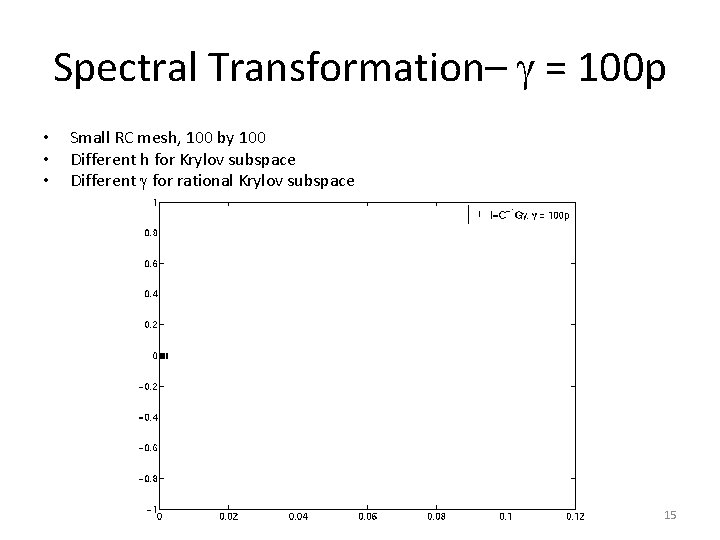
Spectral Transformation– = 100 p • • • Small RC mesh, 100 by 100 Different h for Krylov subspace Different for rational Krylov subspace 15

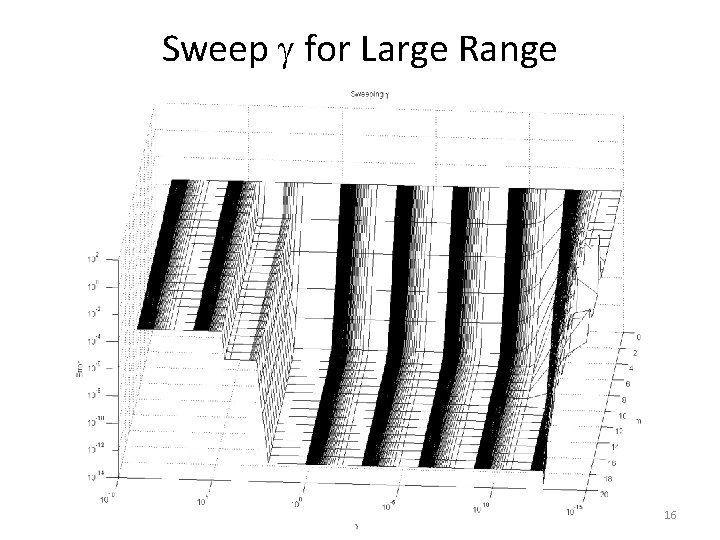
Sweep for Large Range 16

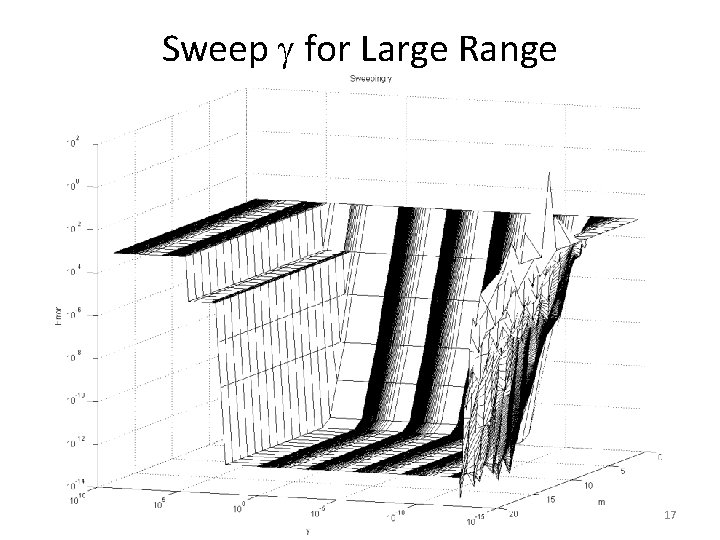
Sweep for Large Range 17

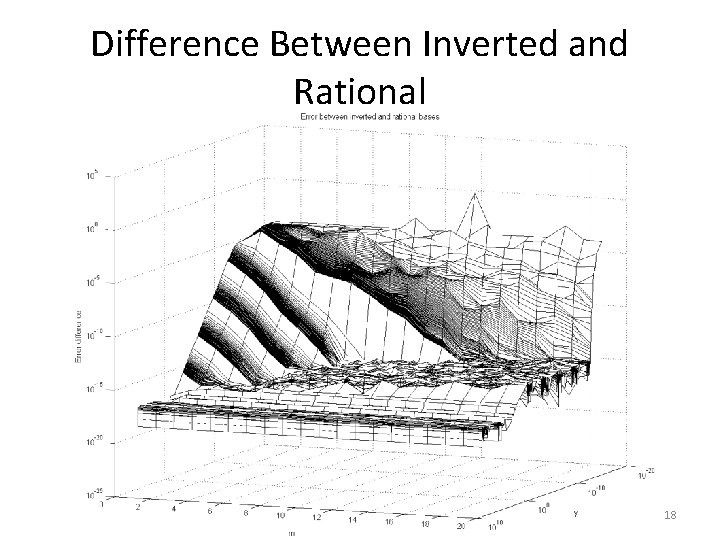
Difference Between Inverted and Rational 18

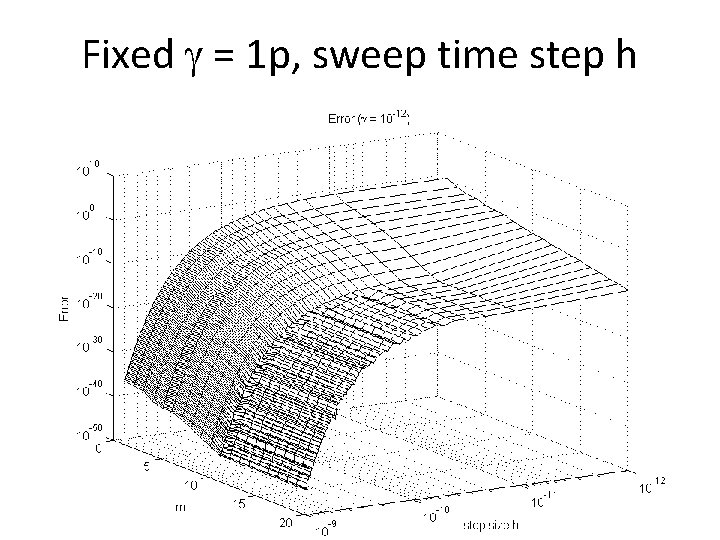
Fixed = 1 p, sweep time step h 19

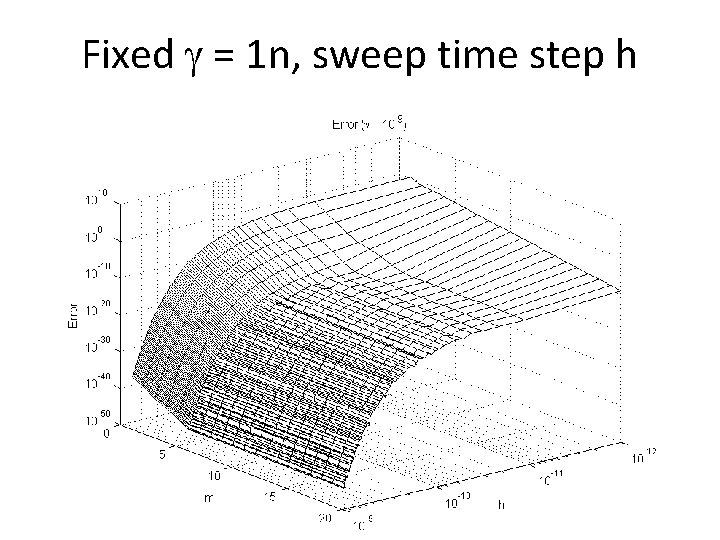
Fixed = 1 n, sweep time step h 20

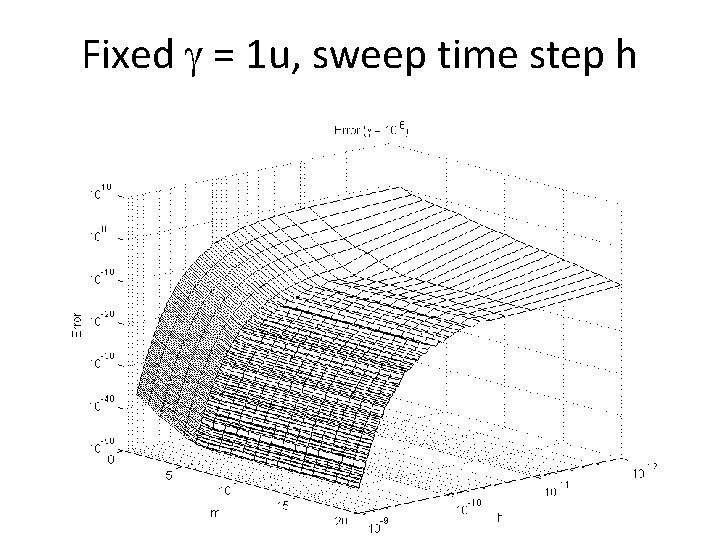
Fixed = 1 u, sweep time step h 21

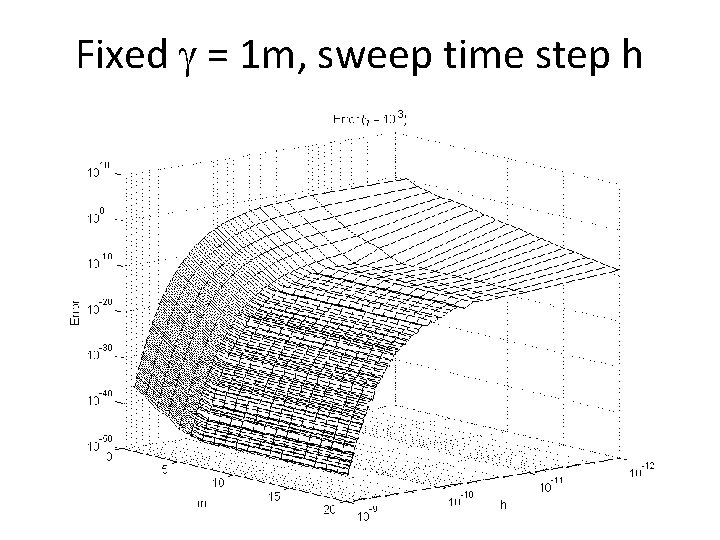
Fixed = 1 m, sweep time step h 22

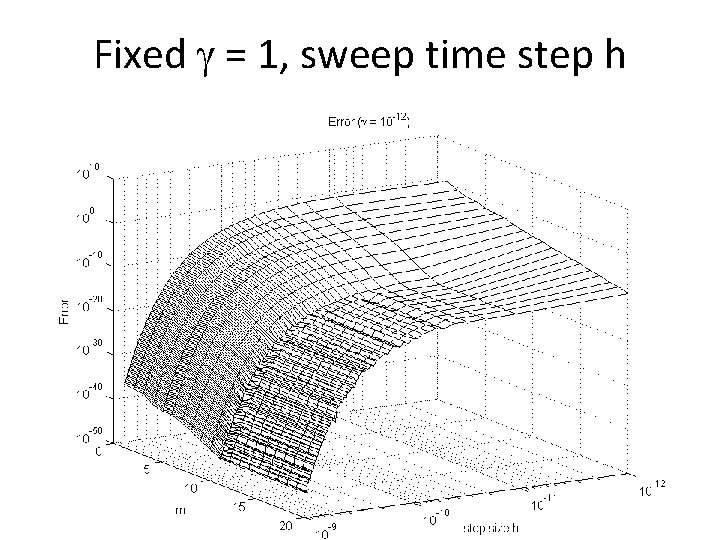
Fixed = 1, sweep time step h 23

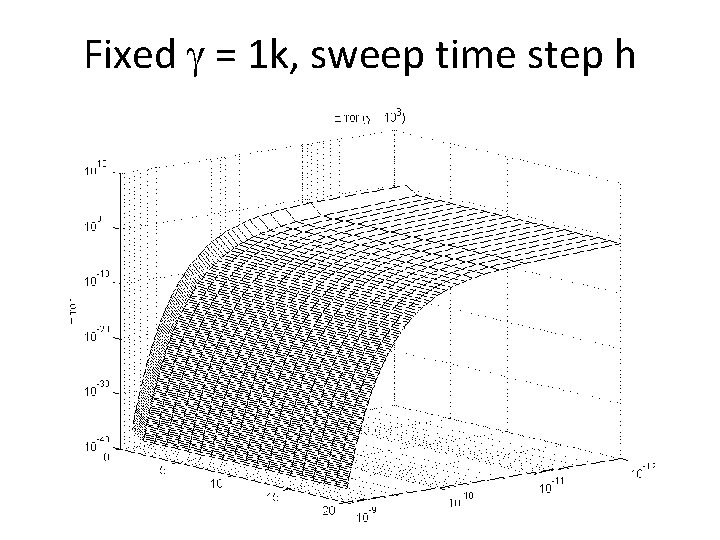
Fixed = 1 k, sweep time step h 24

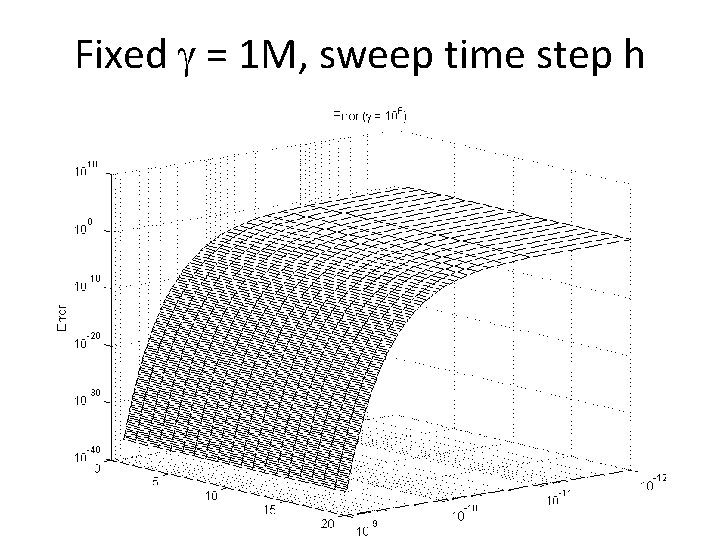
Fixed = 1 M, sweep time step h 25

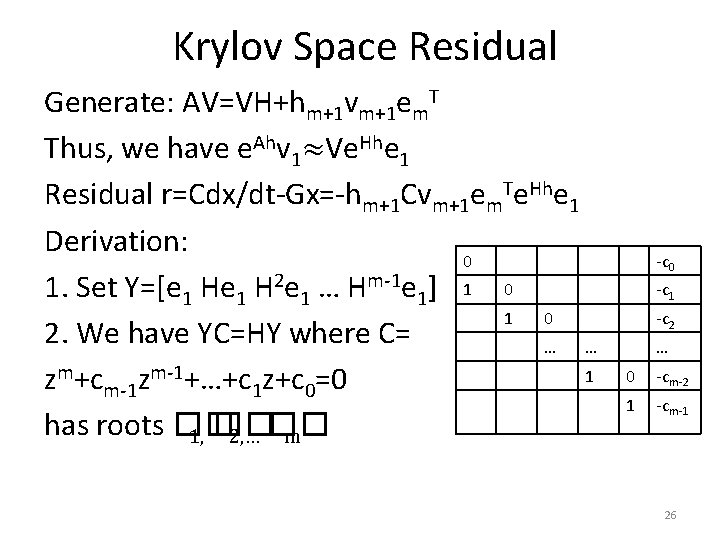
Krylov Space Residual Generate: AV=VH+hm+1 vm+1 em. T Thus, we have e. Ahv 1≈Ve. Hhe 1 Residual r=Cdx/dt-Gx=-hm+1 Cvm+1 em. Te. Hhe 1 Derivation: 0 1. Set Y=[e 1 H 2 e 1 … Hm-1 e 1] 1 0 2. We have YC=HY where C= … … 1 zm+cm-1 zm-1+…+c 1 z+c 0=0 has roots �� 1, �� 2, … �� m -c 0 -c 1 -c 2 … 0 -cm-2 1 -cm-1 26

Krylov Space Residual • 1 ��. 1 m-1 �� 1 1 ��. 2 m-1 �� 2 . . . 1 ��. m m-1 �� m 27

Invert Krylov Space Residual • 28