Circuit Partitioning Presented by Jill 1 Outline l

Circuit Partitioning Presented by Jill 1

Outline l l Introduction Cut-size driven circuit partitioning Multi-objective circuit partitioning Our approach – Network flow based l l Methodology Difficulties 2

Introduction l l What is circuit partitioning ? Circuit partitioning is vital l l Complexity increases Number of transistors involved increases Chip size decreases Partitioning objective l l Cut-size Delay 3

Cut-Size Driven Approach 4

Cut-Size Driven Approach l “Multilevel Hypergraph Partitioning: Application in VLSI Domain” G. Karypis, R. Aggarwal, V. Kumar, S. Shekhar. DAC 1997 l Multilevel hypergraph partitioning algorithm – h. Metis 5

Cut-Size Driven Approach l Three phases: l l l Coarsening Phase Partitioning Phase Uncoarsening and Refinement Phase 6

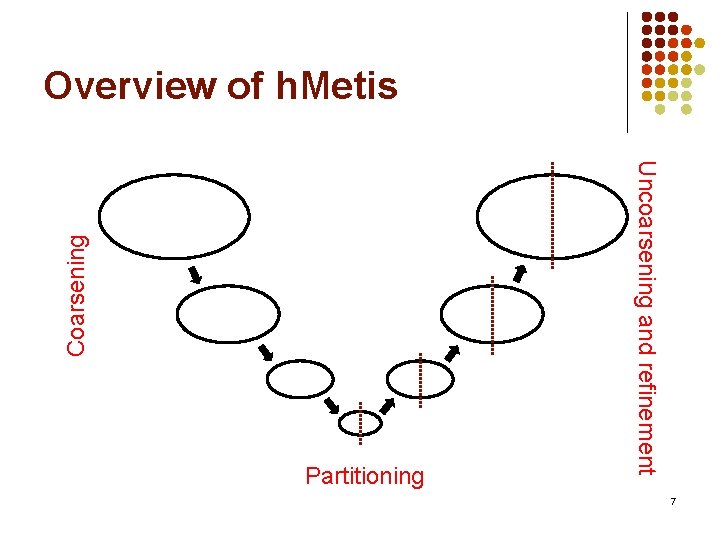
Partitioning Uncoarsening and refinement Coarsening Overview of h. Metis 7

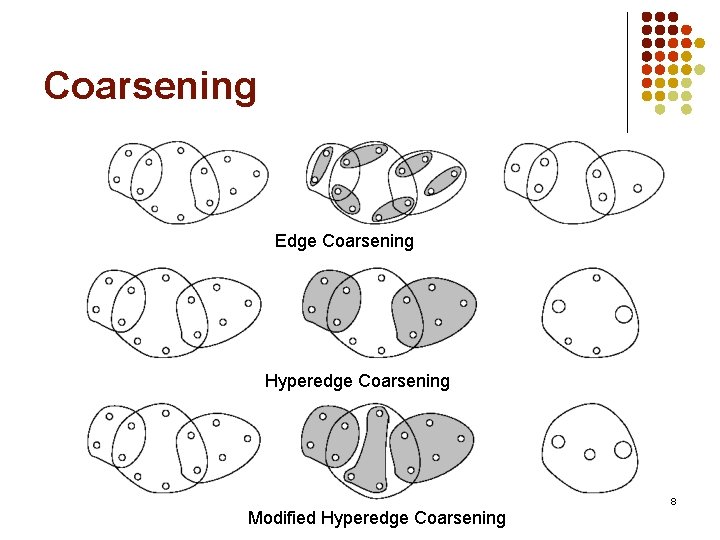
Coarsening Edge Coarsening Hyperedge Coarsening Modified Hyperedge Coarsening 8

Uncoarsening and Refinement l l Successively projecting the partitioning to the next level Refinement: l Early-exit FM l l l Max. number of pass = 2 In each pass, if no improvement after k move, exit Hyperedge Refinement l Remove an entire hyperedge from the cut 9

Multi - Objective Approach 10

Multi-Objective Approach l l “Multi-objective Circuit Partitioning for Cutsize and Path-Based Delay Minimization” C. Ababei, N. Selvakkumaran, K. Bazargan, G. Karypis ICCAD 2002 Multi-objective circuit partitioning based on h. Metis l l Minimize cut-size Minimize delay 11

Multi-Objective Approach l Good solution l l Allow fine-tuned control of the objectives Provide way to handle objectives of different natures Two main differences Objective function l Soln = p 1*C + p 2*D 12

Multi-Objective Approach l Delay l l l Delay of the critical path # of cut along each critical path Edge weight of all edges that lie on the critical path 13

K-Most Critical Paths l l l Partitioning without updating the K-most critical paths Update the list of the K-most critical paths during each move How to choose K? l l Small no improvement Large run time increase, solution space decrease 14

Improvement Over h. Metis l l l Delay 14 % decrease Cut-size 10% increase Run-time 2. 4 x 15

Network Flow Based Approach 16

Network Flow Based Approach l l l Originated by Eric Wong, Prof. Young Delay driven K-way partitioning Three phase: l l l Net modelling Partitioning phase Refinement phase 17

Net Modelling l l As network flow technique is used, circuits should be modelled as graph Acyclic partitioning for the following paths: l l PI PO PI FF FF PO 18

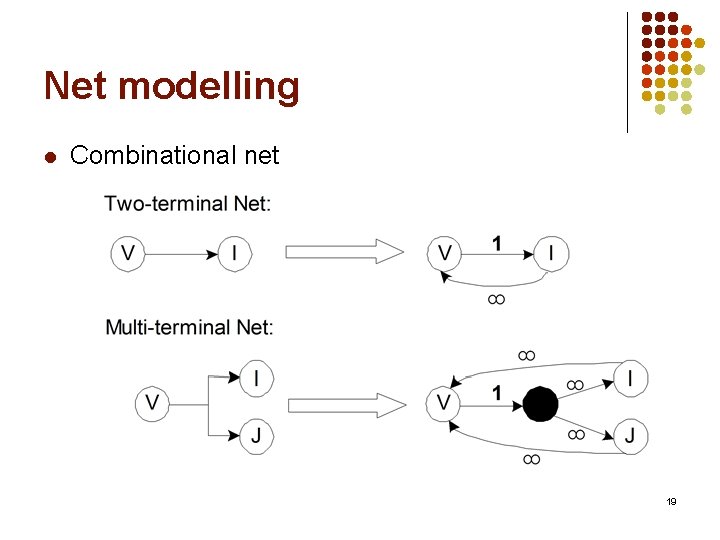
Net modelling l Combinational net 19

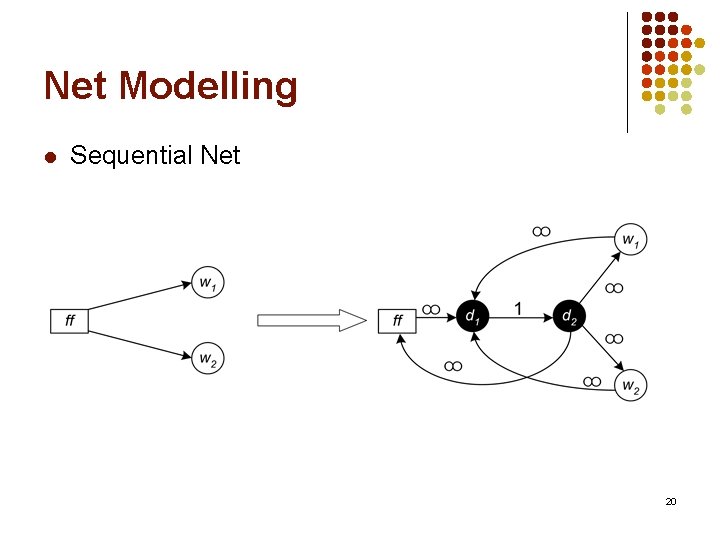
Net Modelling l Sequential Net 20

Partitioning Phase l Max-Flow Min-Cut l l l Guarantee min-cut Not necessarily balanced “Efficient Network Flow Based Min-Cut Balanced Partitioning” Honghua Yang, D. F. Wong ICCAD 1994 21

Partitioning Phase 22

Partitioning Phase l l How to select from the larger partition ? If > threshold l l If < threshold l l l Random select Try all possible choices Follow acyclic constraint Apply the partitioning phase recursively to obtain k-way partitioning 23

Refinement Phase l l l FM post-processing step Apply FM to every pair of partition Different from original FM l l If delay increased, reject May yield cyclic result 24

Experimental results l l 1 to 2. xls 1 to 5. xls 25

Difficuties l Possible reason: l l Ratio increased % decreased Method of bipartitioning Acyclic restriction Future Direction l Cyclic ? Acyclic ? 26