Circuit Equations Tableau Equations KCL KVL EE Resistive

Circuit Equations (Tableau Equations) KCL: KVL: EE:

Resistive circuits can be modelled by algebraic equations in time domain. All linear circuits in sinusoidal steady state can be modelled by algebraic equations in frequency domain. §. . . are vectors of time functions. §. . . are vectors of phasors. § Elements of T are real. § Elements of T(w) can be complex. § The circuit is modelled by linear algebraic equations with real coefficients. § The circuit is modelled by linear algebraic equations with complex coefficients.

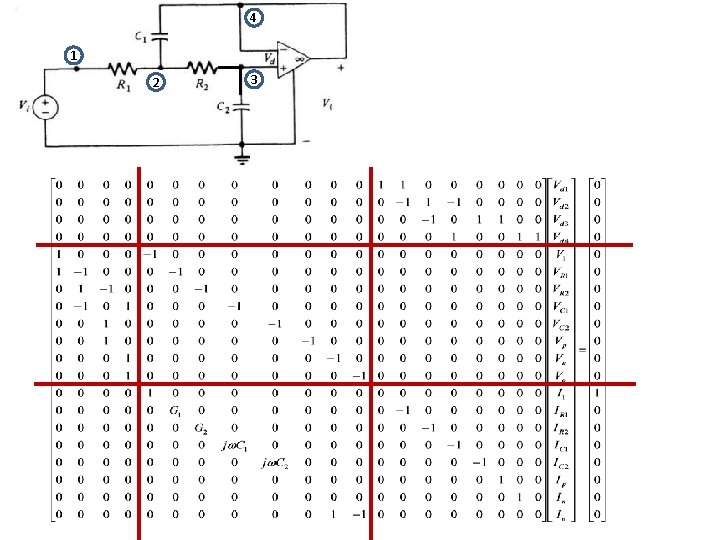
4 1 2 v 3

Generalized Node Analysis KCL Equations: KVL Equations: Group the elements into two classes: 1. class: voltage-controlled elements 2. class: not voltage-controlled elements Method: Step 1: Write KCL equations for nodes: Step 2: Substitute voltage controlled element equations for the elements in the 1. class and for the 2. class write EE’s:

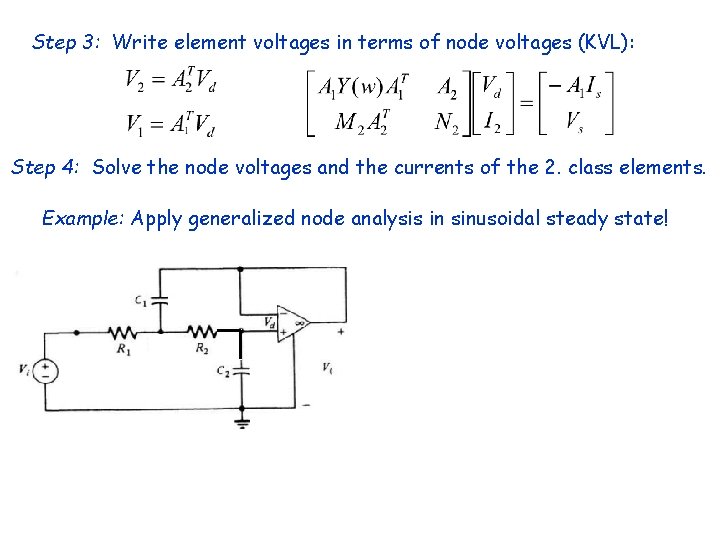
Step 3: Write element voltages in terms of node voltages (KVL): Step 4: Solve the node voltages and the currents of the 2. class elements. Example: Apply generalized node analysis in sinusoidal steady state! v

Generalized Mesh Analysis KCL Equations: KVL Equations: Group the elements into two classes: 1. class: current-controlled elements 2. class: not current-controlled elements Method: Step 1: Write KVL equations for meshes: Step 2: Substitute current-controlled element equations for the elements in the 1. class and for the 2. class write EE’s:

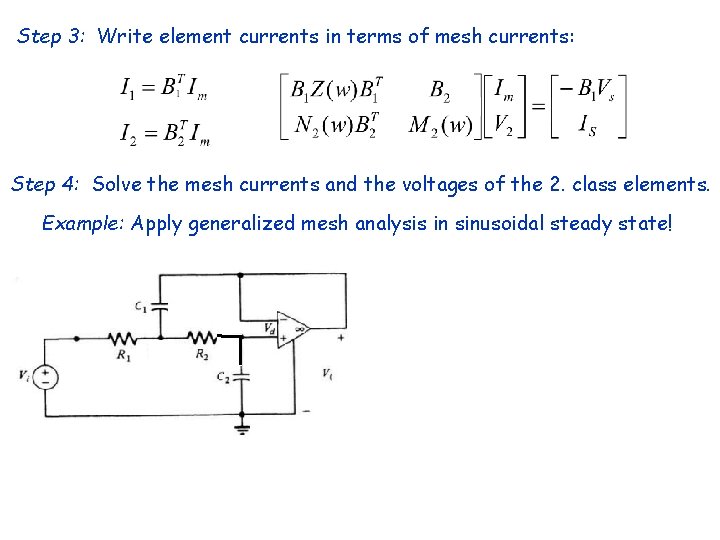
Step 3: Write element currents in terms of mesh currents: Step 4: Solve the mesh currents and the voltages of the 2. class elements. Example: Apply generalized mesh analysis in sinusoidal steady state! v

Additivity and Multiplicativity Theorem: (Additivity) Consider a circuit with linear resistors and independent sources. Group 1 Group 2 Solve the circuit when only sources in Group 1 are active whereas sources in Group 2 are set to zero Then, the solution when all the sources are active is Theorem: (Multiplicativity) Consider a circuit with linear resistors and independent sources. Assume that solutions are. If independent sources are set to solutions are. ,

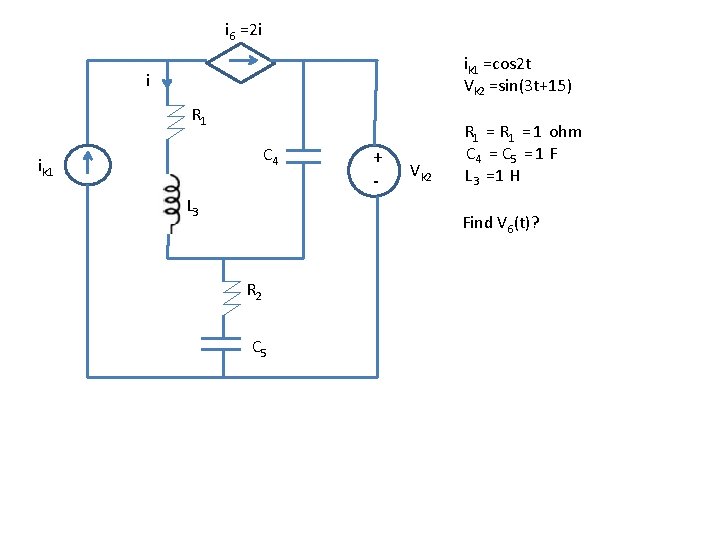
i 6 =2 i ik 1 =cos 2 t Vk 2 =sin(3 t+15) i R 1 C 4 ik 1 L 3 + - Vk 2 R 1 = 1 ohm C 4 = C 5 = 1 F L 3 =1 H Find V 6(t)? R 2 C 5