Circles Revision Transformations Intercepts Using the discriminant Chords

Circles Revision Transformations • Intercepts • Using the discriminant • Chords •

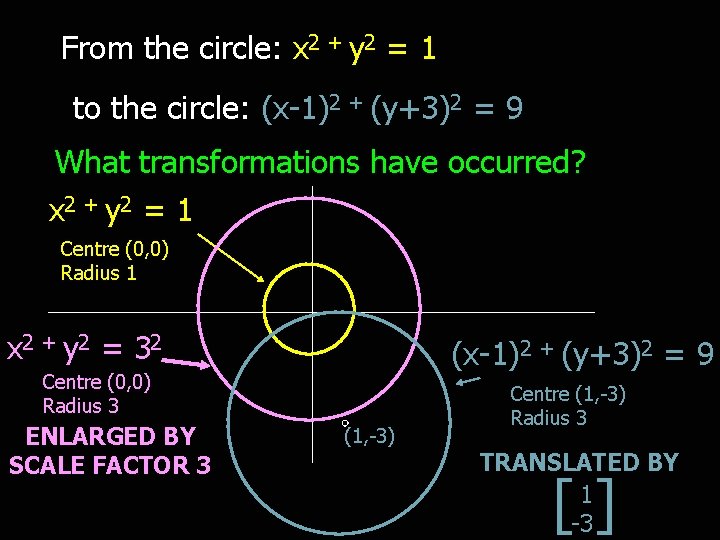
From the circle: x 2 + y 2 = 1 to the circle: (x-1)2 + (y+3)2 = 9 What transformations have occurred? x 2 + y 2 = 1 Centre (0, 0) Radius 1 x 2 + y 2 = 3 2 (x-1)2 + (y+3)2 = 9 Centre (0, 0) Radius 3 ENLARGED BY SCALE FACTOR 3 (1, -3) Centre (1, -3) Radius 3 TRANSLATED BY 1 -3 []

Where do they intersect? For the circle: (x-1)2 + (y-3)2 = 9. . and the line y = x +10 Where do they cross? Solve simultaneously to find intersect … 2 – 2 x +1) + 2 2 (x (x-1) + (y-3) = 9 2 + 14 x + 49) = 9 (x y = x +10 Substitute y: 2 x 2 + 12 x + 41 = 0 (x-1)2 + (x +10 -3)2 = 9 Solve equation to find intersect (x-1)2 + (x +7)2 = 9

Circle Intersect Does 2 x 2 + 12 x+41=0 have real roots Use discriminent “b 2 -4 ac” To find out about roots a = [coefficient of x 2] = 2 b = [coefficient of x] = 12 c= [constant] = 41 b 2 - 4 ac = 122 – (4 x 2 x 41) = 144 – 328 = -184 “b 2 – 4 ac < 0” No roots (solutions)

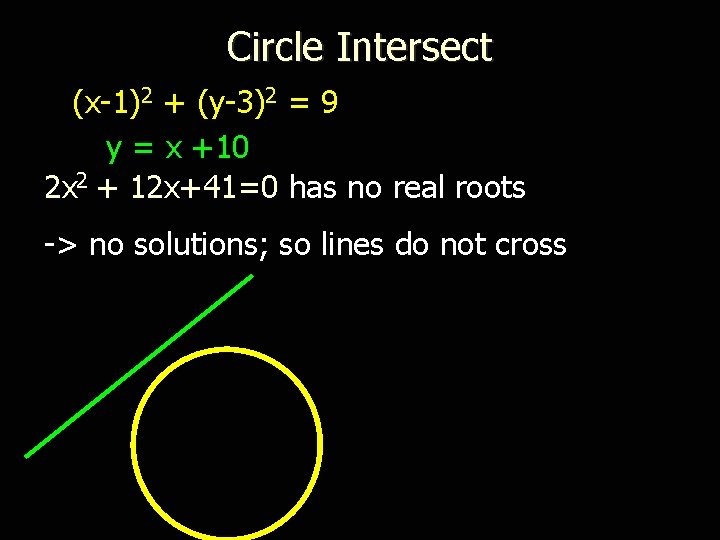
Circle Intersect (x-1)2 + (y-3)2 = 9 y = x +10 2 x 2 + 12 x+41=0 has no real roots -> no solutions; so lines do not cross

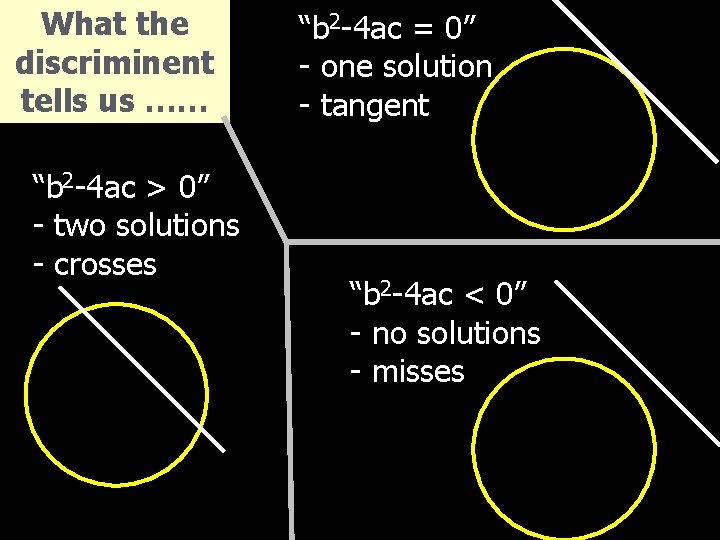
What the discriminent tells us …… “b 2 -4 ac > 0” - two solutions - crosses “b 2 -4 ac = 0” - one solution - tangent “b 2 -4 ac < 0” - no solutions - misses

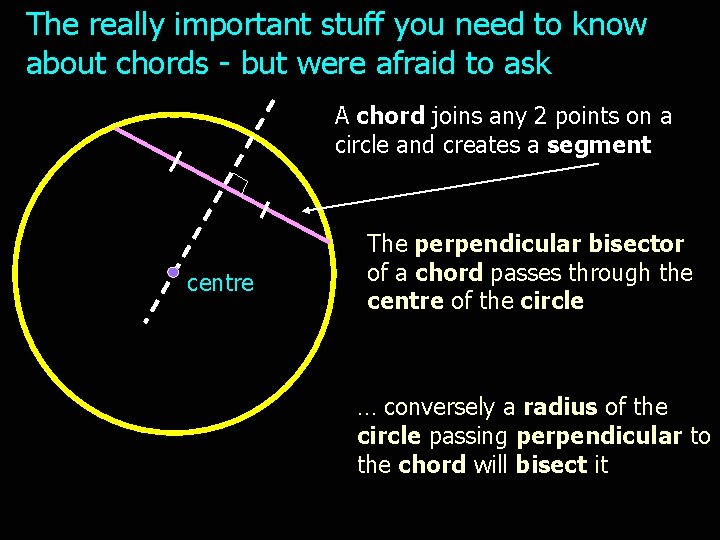
The really important stuff you need to know about chords - but were afraid to ask A chord joins any 2 points on a circle and creates a segment centre The perpendicular bisector of a chord passes through the centre of the circle … conversely a radius of the circle passing perpendicular to the chord will bisect it

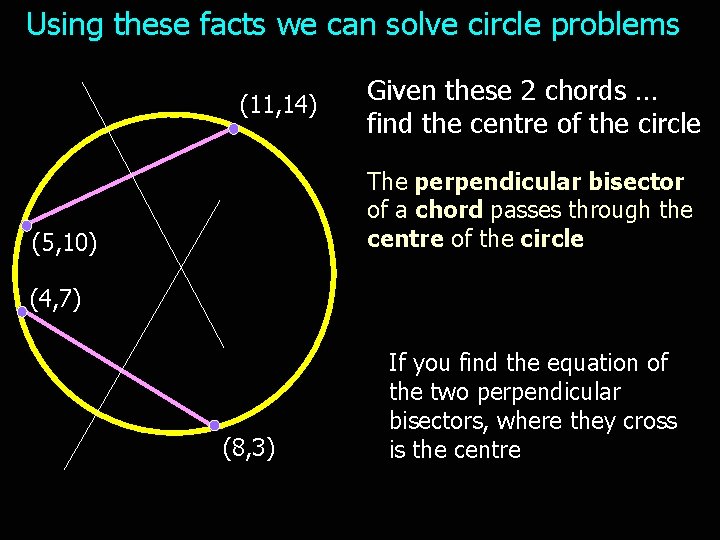
Using these facts we can solve circle problems (11, 14) Given these 2 chords … find the centre of the circle The perpendicular bisector of a chord passes through the centre of the circle (5, 10) (4, 7) (8, 3) If you find the equation of the two perpendicular bisectors, where they cross is the centre

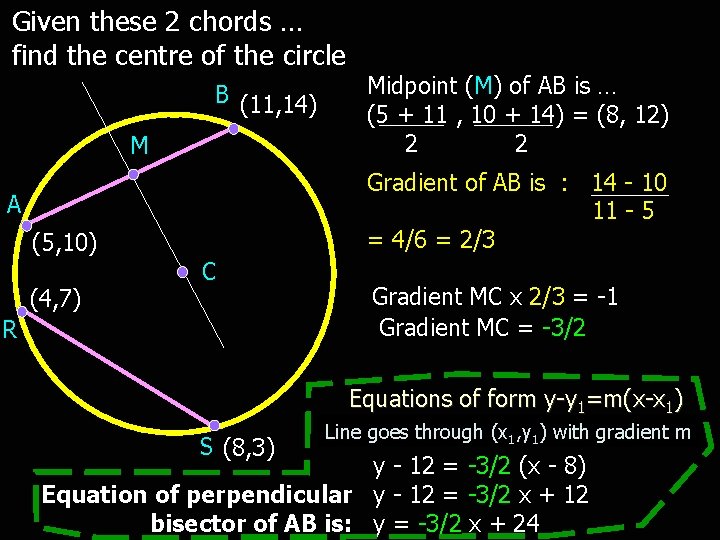
Given these 2 chords … find the centre of the circle B (11, 14) M Gradient of AB is : 14 - 10 11 - 5 = 4/6 = 2/3 A (5, 10) (4, 7) Midpoint (M) of AB is … (5 + 11 , 10 + 14) = (8, 12) 2 2 C R Gradient MC x 2/3 = -1 Gradient MC = -3/2 Equations of form y-y 1=m(x-x 1) S (8, 3) Line goes through (x 1, y 1) with gradient m y - 12 = -3/2 (x - 8) Equation of perpendicular y - 12 = -3/2 x + 12 bisector of AB is: y = -3/2 x + 24

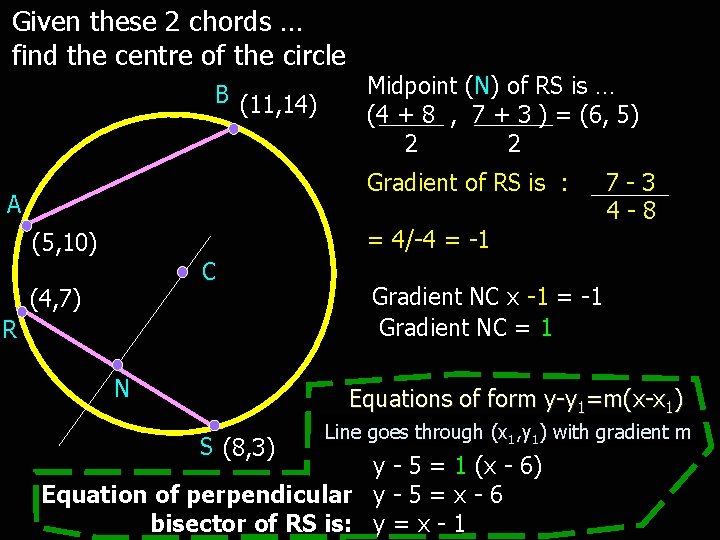
Given these 2 chords … find the centre of the circle B (11, 14) Midpoint (N) of RS is … (4 + 8 , 7 + 3 ) = (6, 5) 2 2 Gradient of RS is : A = 4/-4 = -1 (5, 10) C (4, 7) R N 7 -3 4 -8 Gradient NC x -1 = -1 Gradient NC = 1 Equations of form y-y 1=m(x-x 1) S (8, 3) Line goes through (x 1, y 1) with gradient m y - 5 = 1 (x - 6) Equation of perpendicular y - 5 = x - 6 bisector of RS is: y = x - 1

Finding the centre …. y = -3/2 x + 24 (11, 14) If you find the equation of the two perpendicular bisectors, where they cross is the centre y=x-1 - y = -3/2 x + 24 (5, 10) (4, 7) subtract 0 = x - -3/2 x -1 - 24 C 5/2 x -25 = 0 5/2 x = 25 5 x = 50 x = 10 y=x-1 (8, 3) y = 10 -1 = 9 Centre is at (10, 9)