Circles Outcome 4 Equations of a circle The

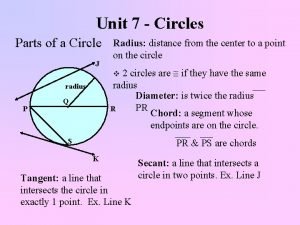
Circles (Outcome 4) – Equations of a circle The equation of a circle with centre (0, 0) and radius r is x² + y² = r². A circle is defined as the locus of all the points that are a fixed distance from the centre point. Example 1 Find the equation of a circle with centre (0, 0) and a radius of 2√ 2. Solution x² + y² = r² x² + y² = (2√ 2 )² x² + y² = 8

Circles (Outcome 4) – Equations of a circle The equation of a circle with centre (a, b) and radius r is (x - a)² + (y - b)² = r². Example 2 Find the centre and radius of the circle (x + 4)² + (y - 6)² = 1 Solution (x – (-4))² + (y - 6)² = 1 Centre (-4, 6) r² = 1 r = √ 1 Radius = 1

Circles (Outcome 4) – Equations of a circle The equation of the circle can be written in an expanded form. Example 3 The equation of the circle (x - 1)² + (y - 2)² = 16. Write the equation without brackets. (1, 2) Solution (x – 1)² + (y - 2)² = 16 x² - 2 x + 1 + y² - 4 y + 4 – 16 = 0 x² + y² - 2 x - 4 y – 12 = 0

Circles (Outcome 4) – Equations of a circle The equation of the circle can be written in an expanded form. Example 4 Show that x² + y² + 4 x - 8 y - 5 = 0 is the equation of a circle. Find the radius and centre of the circle. Solution x² + y² + 4 x – 8 y - 5 = 0 x² + 4 x + y² - 8 y - 5 = 0 (x + 2)² - 4 + (y - 4)² - 16 - 5 = 0 (x + 2)² + (y - 4)² - 25 = 0 (x + 2)² + (y - 4)² = 25 (x - (-2)² + (y - 4)² = 5² The centre is (-2, 4) and the radius is 5.

Circles (Outcome 4) – Equations of a circle The general equation of a circle is of the form x² + y² + 2 gx + 2 fy + c = 0. From the general form of the circle equation, x² + y² + 2 gx + 2 fy + c = 0 The centre of the circle is (-g, -f) The circle radius is √g² + f² - c Note that g² + f² - c > 0. Proof x² + y² + 2 gx + 2 fy + c = 0 x² + 2 gx + y² + 2 fy + c = 0 (x + g)² - g² + (y + f)² - f² + c = 0 (x + g)² + (y + f)² = g² + f² - c (x - (-g))² + (y - (-f))² = g² + f² - c From the above, the circle centre is (-g, -f) and the radius is √g² + f² - c.

Trigonometry (Outcome 4) – Equations of a circle The general equation of a circle is of the form x² + y² + 2 gx + 2 fy + c = 0. Example 5 What is the radius and centre of the circle x² + y² + 4 x - 8 y - 5 = 0? Solution x² + y² + 4 x - 8 y - 5 = 0 x² + y² + 2 gx + 2 fy + c = 0 2 g = 4, 2 f = - 8, c= - 5 g = 2, f = - 4, c= - 5 The circle centre is (-g, -f) = (-2, 4). The radius is √g² + f² - c = √ 2² + (-4)² - (-5) = √ 4 + 16 + 5 = √ 25 =5

Circles (Outcome 4) – Equations of a circle The general equation of a circle is of the form x² + y² + 2 gx + 2 fy + c = 0. Example 6 For the circle x² + y² + 4 x - 8 y - 5 = 0 state whether the each of the following points lies inside, outside or on the circle. A (-2, -1), B (1, 2) C (3, 1) Solution i) When x = -2 and y = -1 x² + y² + 4 x - 8 y – 5 = (-2)² + (-1)² + 4 x(-2) – 8 x(-1) – 5 = 0 As x² + y² + 4 x - 8 y – 5 = 0, A(-2, -1) lies on the circumference of the circle. ii) When x = 1 and y = 2 x² + y² + 4 x - 8 y – 5 = 1² + 2² + 4 x 1 – 8 x 2 – 5 = -12 As x² + y² + 4 x - 8 y – 5 < 0, B(1, 2) lies inside the circle. iii) When x = 3 and y = 1 x² + y² + 4 x - 8 y – 5 = 3² + 1² + 4 x 3 – 8 x 1 – 5 = 9 As x² + y² + 4 x - 8 y – 5 > 0, C (3, 1) lies outside the circle.

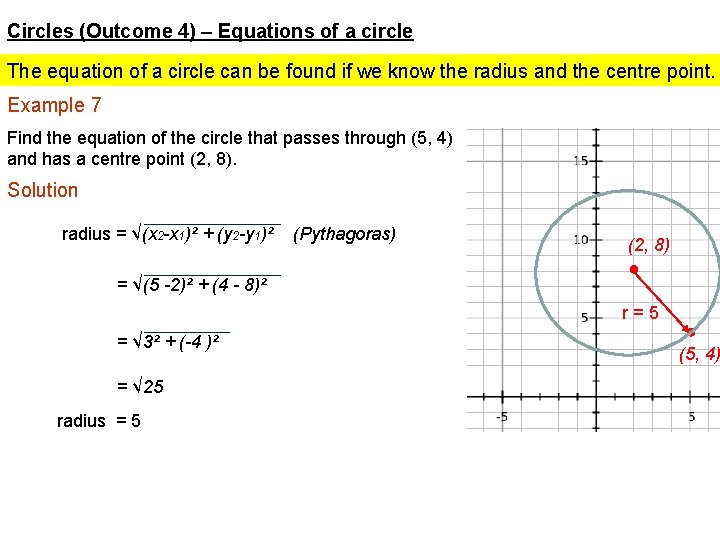
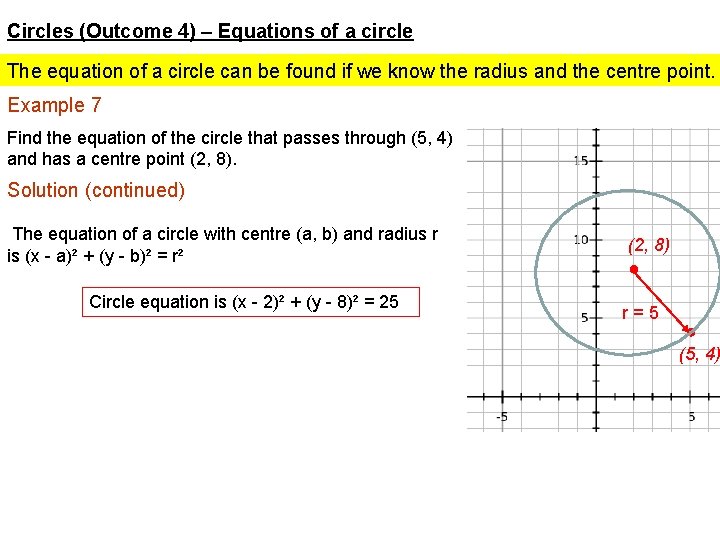
Circles (Outcome 4) – Equations of a circle The equation of a circle can be found if we know the radius and the centre point. Example 7 Find the equation of the circle that passes through (5, 4) and has a centre point (2, 8). Solution radius = √(x 2 -x 1)² + (y 2 -y 1)² = √(5 -2)² + (4 - 8)² (Pythagoras) (2, 8) ● r=5 = √ 3² + (-4 )² = √ 25 radius = 5 ● (5, 4)

Circles (Outcome 4) – Equations of a circle The equation of a circle can be found if we know the radius and the centre point. Example 7 Find the equation of the circle that passes through (5, 4) and has a centre point (2, 8). Solution (continued) The equation of a circle with centre (a, b) and radius r is (x - a)² + (y - b)² = r² Circle equation is (x - 2)² + (y - 8)² = 25 (2, 8) ● r=5 ● (5, 4)

Circles (Outcome 4) – Equations of a circle The general equation of a circle is valid when g² + f² - c > 0. Example 8 For what values of k is x² + y² + 2 x – 4 y + k = 0 not the equation of a circle? Solution The general equation of a circle is invalid when g² + f² - c < 0 For x² + y² + 2 x – 4 y + k = 0 x² + y² + 2 gx + 2 fy + c = 0 2 g = 2, 2 f = - 4, c= k g = 1, f = - 2, c= k g² + f² - c = 1² + (-2)² - k g² + f² - c = 5 - k For an invalid circle, 5 - k < 0 k>5

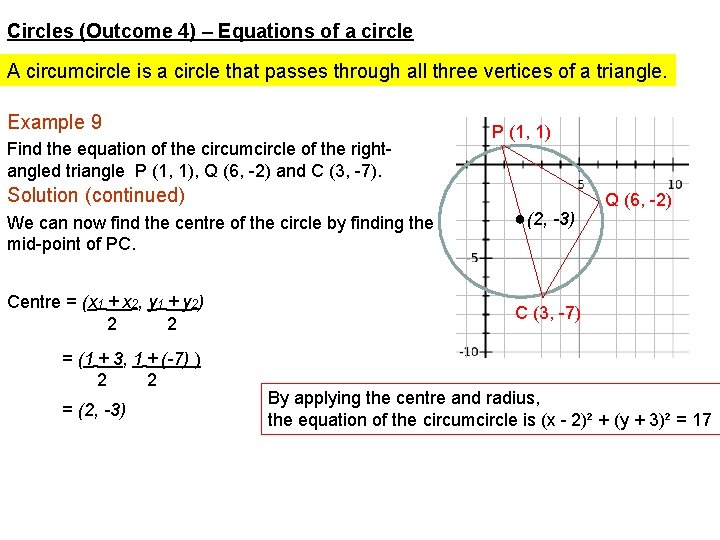
Circles (Outcome 4) – Equations of a circle A circumcircle is a circle that passes through all three vertices of a triangle. Example 9 Find the equation of the circumcircle of the rightangled triangle P (1, 1), Q (6, -2) and C (3, -7). P (1, 1) Solution Q (6, -2) For a right-angled triangle, the hypotenuse is the diameter of the circle. Therefore, if we find the length of the diameter PC, we can find the radius. Length of PC = √(x 2 -x 1)² + (y 2 -y 1)² (Pythagoras) = √(3 -1)² + ((-7) - 1)² = √ 2² + (-8 )² = √ 68 Radius = √ 68 ÷ 2 = 2√ 17 ÷ 2 = √ 17 C (3, -7)

Circles (Outcome 4) – Equations of a circle A circumcircle is a circle that passes through all three vertices of a triangle. Example 9 Find the equation of the circumcircle of the rightangled triangle P (1, 1), Q (6, -2) and C (3, -7). P (1, 1) Solution (continued) We can now find the centre of the circle by finding the mid-point of PC. Centre = (x 1 + x 2, y 1 + y 2) 2 2 = (1 + 3, 1 + (-7) ) 2 2 = (2, -3) ●(2, -3) Q (6, -2) C (3, -7) By applying the centre and radius, the equation of the circumcircle is (x - 2)² + (y + 3)² = 17