Circles Basic Terms A circle is the set
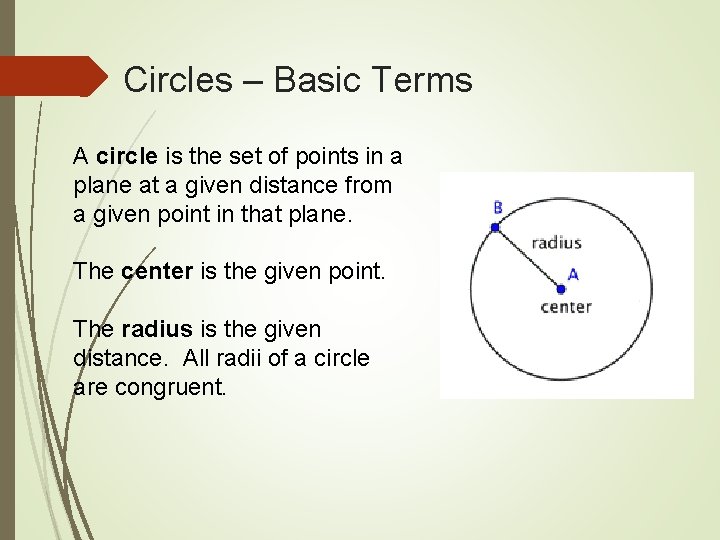
Circles – Basic Terms A circle is the set of points in a plane at a given distance from a given point in that plane. The center is the given point. The radius is the given distance. All radii of a circle are congruent.
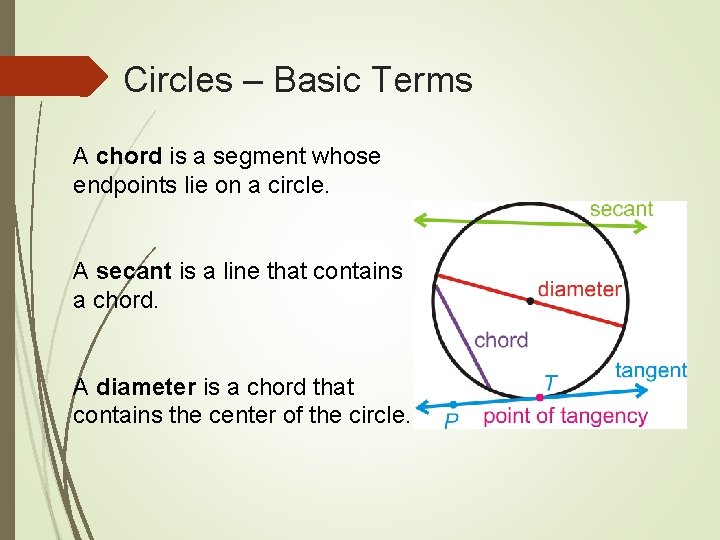
Circles – Basic Terms A chord is a segment whose endpoints lie on a circle. A secant is a line that contains a chord. A diameter is a chord that contains the center of the circle.
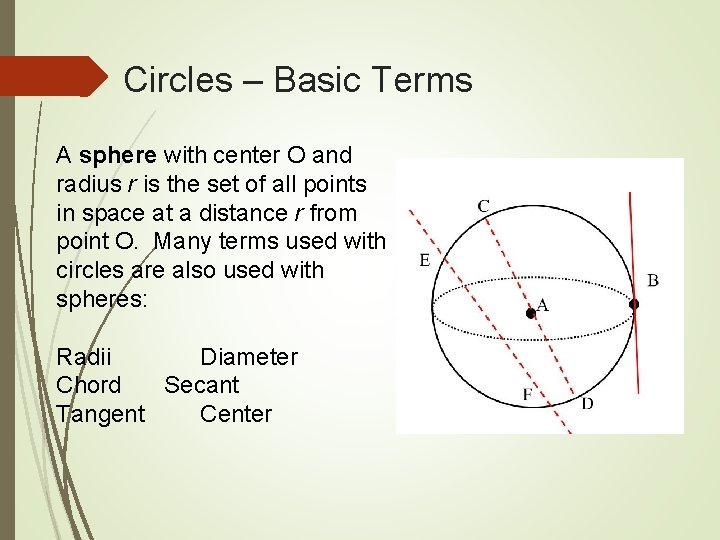
Circles – Basic Terms A sphere with center O and radius r is the set of all points in space at a distance r from point O. Many terms used with circles are also used with spheres: Radii Diameter Chord Secant Tangent Center
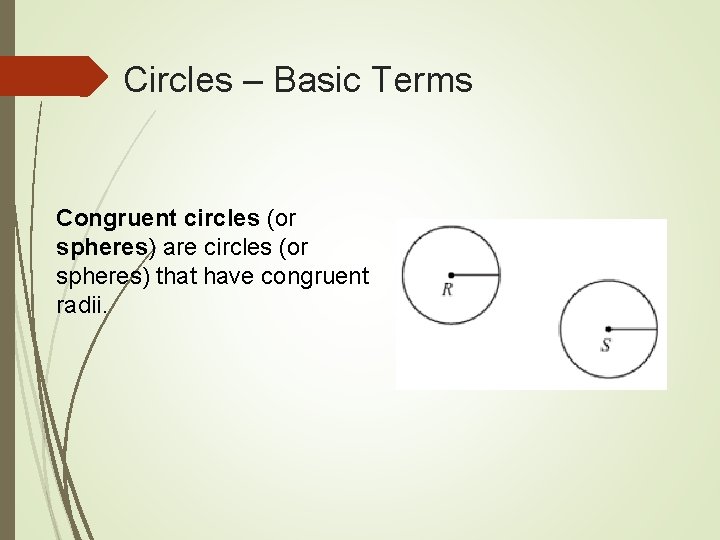
Circles – Basic Terms Congruent circles (or spheres) are circles (or spheres) that have congruent radii.
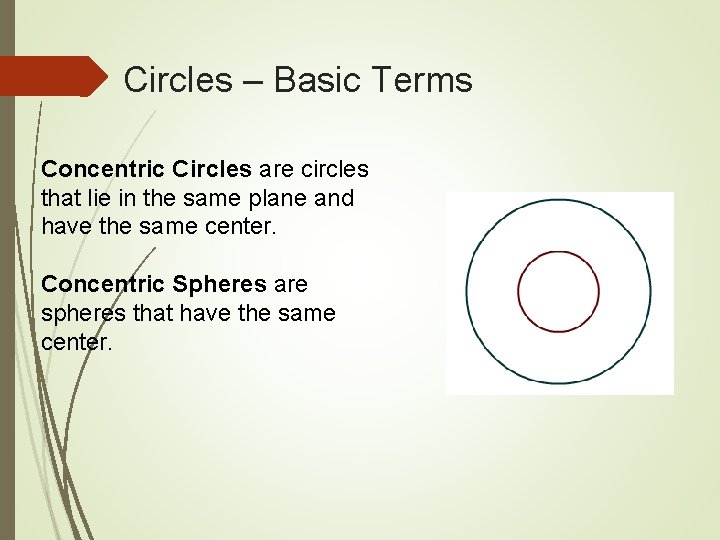
Circles – Basic Terms Concentric Circles are circles that lie in the same plane and have the same center. Concentric Spheres are spheres that have the same center.
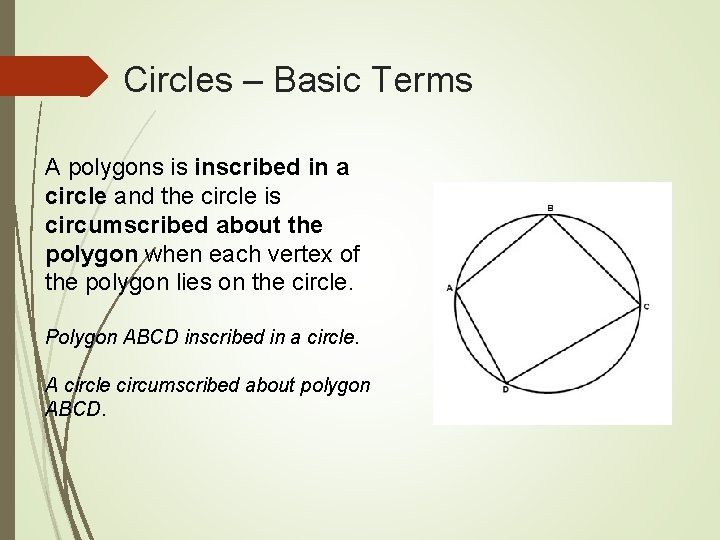
Circles – Basic Terms A polygons is inscribed in a circle and the circle is circumscribed about the polygon when each vertex of the polygon lies on the circle. Polygon ABCD inscribed in a circle. A circle circumscribed about polygon ABCD.

Learning Log Summary LT 1 - I can apply theorems that relate to tangents and radii in proof and problem solving. Key vocabulary for circles includes… A tangent line is…

Proof by Contradiction “When you have eliminated all which is impossible, then whatever remains, however improbable, must be the truth. ” -Sir Arthur Conan Doyle

Proof by Contradiction Trying to prove: If p, then q. Assume: “not q” Show: this assumption leads to a contradiction, so the original conclusion must be true.

Proof by Contradiction
Proof by Contradiction
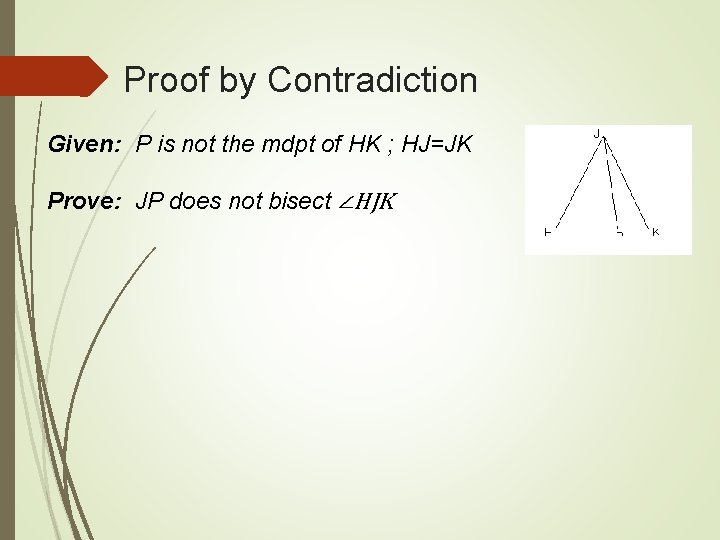
Proof by Contradiction Given: P is not the mdpt of HK ; HJ=JK Prove: JP does not bisect ∠HJK

Learning Log Summary LT 2 - I can use indirect proof to prove an algebraic or geometric statement. The steps to indirect proof are… The goal in a proof by contradiction is…

Theorem 9 -1 http: //bit. ly/2 kyqb. Qk

Theorem 9 -1 PARTNER A • Describe the assumption you will make. PARTNER B • Explain why your partner is making this assumption. • Re-state each step of your partner’s reasoning, asking clarifying questions. • Explain each step of your reasoning, including the justification for that step. • Explain clearly where the contradiction is! • What is the conclusion that can be drawn?
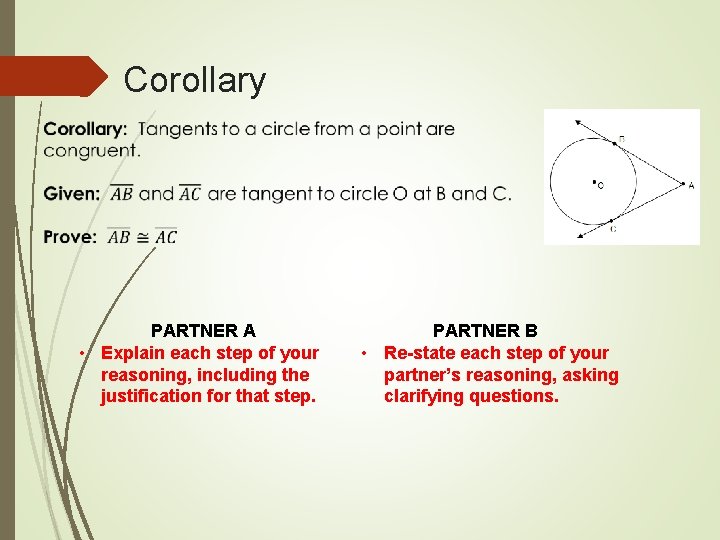
Corollary PARTNER A • Explain each step of your reasoning, including the justification for that step. PARTNER B • Re-state each step of your partner’s reasoning, asking clarifying questions.

Theorem 9 -2 PARTNER B • Describe the assumption you will make. PARTNER A • Explain why your partner is making this assumption. • Re-state each step of your partner’s reasoning, asking clarifying questions. • Explain each step of your reasoning, including the justification for that step. • Explain clearly where the contradiction is! • What is the conclusion that can be drawn?

Applying Theorems About Radii and Tangents Explain and/or justify the steps you took to complete the following problems:
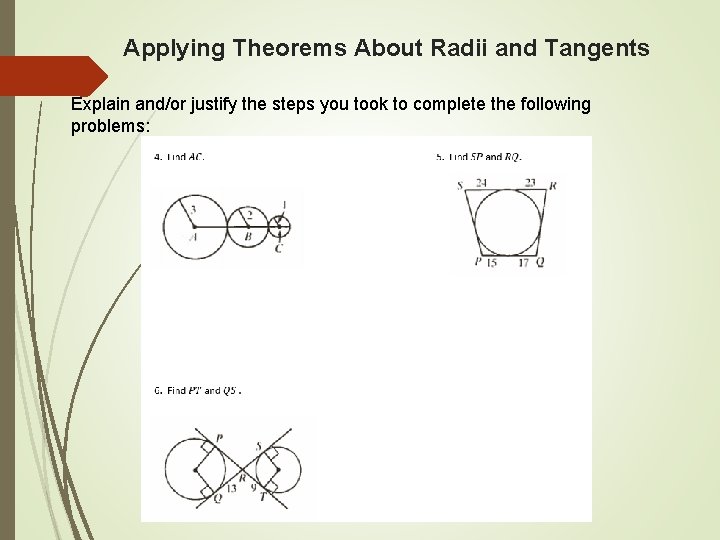
Applying Theorems About Radii and Tangents Explain and/or justify the steps you took to complete the following problems:

Learning Log Summary LT 3 - I can use indirect proof to show that the tangent is perpendicular to the radius of a circle drawn at the point of tangency. To prove the tangent is perpendicular to the radius at the point of tangency… The contradiction in this proof is created by…

Learning Log Summary LT 9 - I can construct a tangent through a point on the circle and through a point outside the circle. LT 10 - I can explain the relevant geometry involved in the construction of a tangent line from a point outside of the circle.
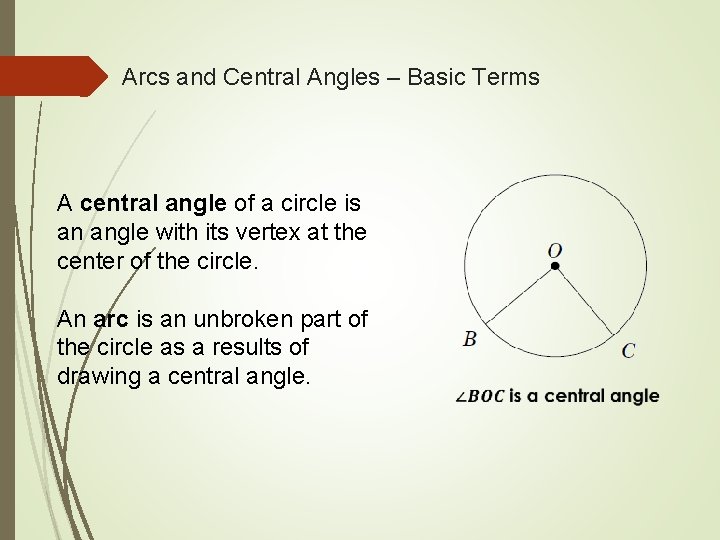
Arcs and Central Angles – Basic Terms A central angle of a circle is an angle with its vertex at the center of the circle. An arc is an unbroken part of the circle as a results of drawing a central angle.
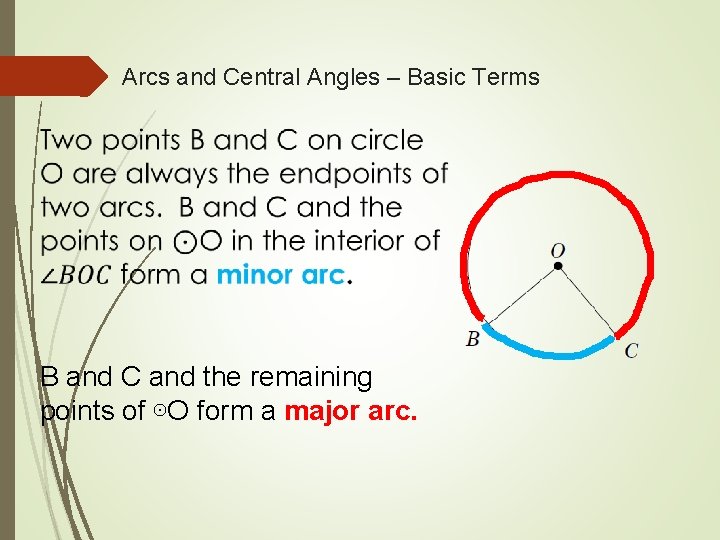
Arcs and Central Angles – Basic Terms B and C and the remaining points of ⊙O form a major arc.
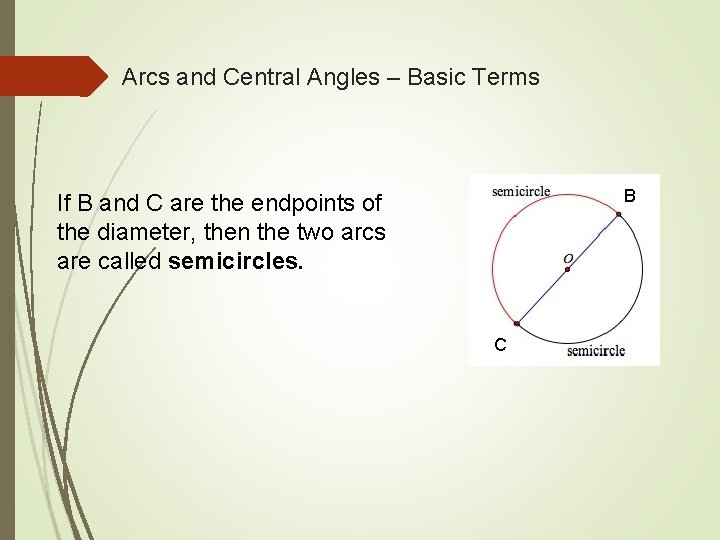
Arcs and Central Angles – Basic Terms B If B and C are the endpoints of the diameter, then the two arcs are called semicircles. C
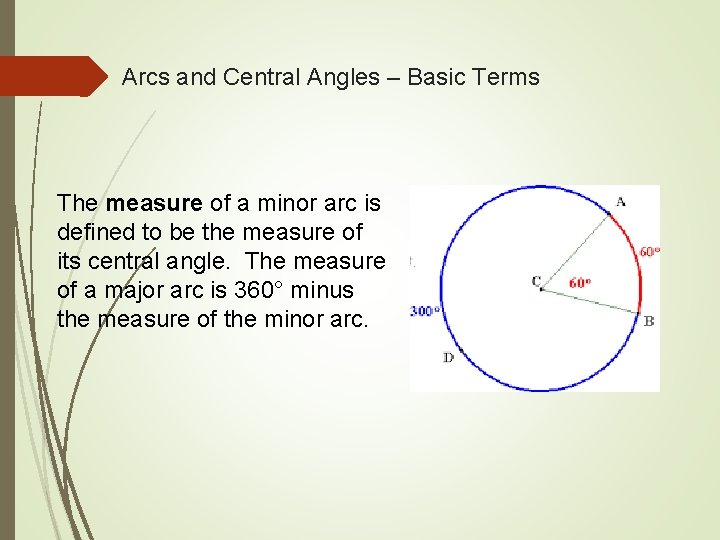
Arcs and Central Angles – Basic Terms The measure of a minor arc is defined to be the measure of its central angle. The measure of a major arc is 360° minus the measure of the minor arc.
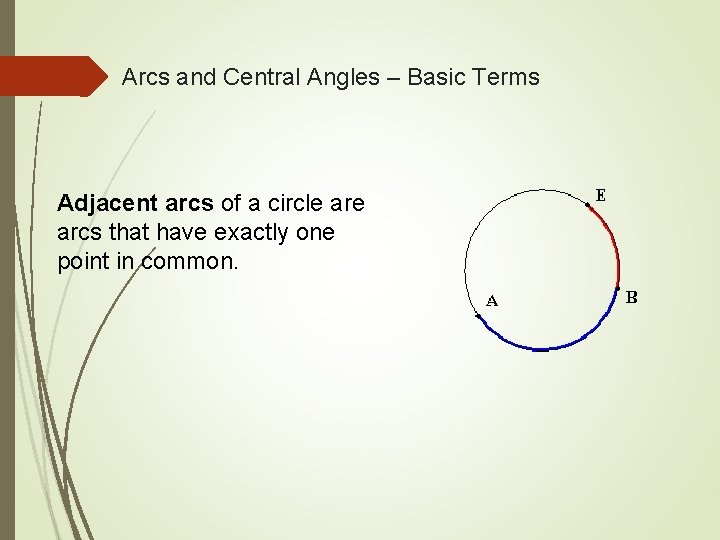
Arcs and Central Angles – Basic Terms Adjacent arcs of a circle arcs that have exactly one point in common.

Arcs and Central Angles – Basic Terms Arc Addition Postulate: The measure of the arc formed by two adjacent arcs is the sum of the measures of these two arcs.
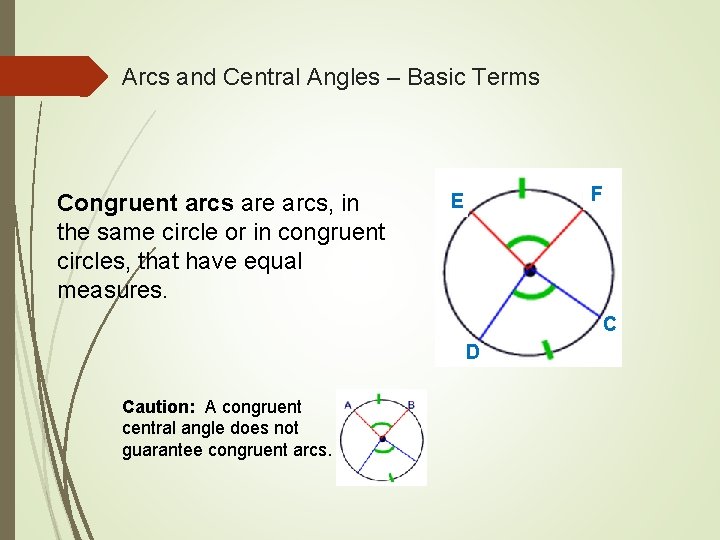
Arcs and Central Angles – Basic Terms Congruent arcs are arcs, in the same circle or in congruent circles, that have equal measures. F E C D Caution: A congruent central angle does not guarantee congruent arcs.
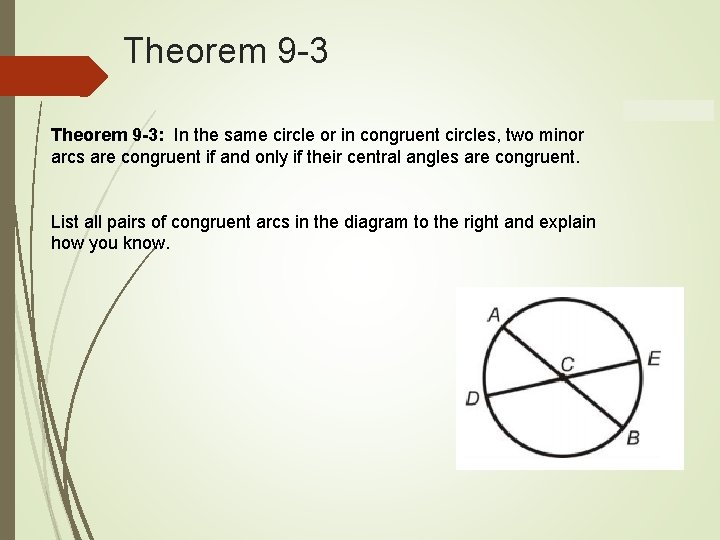
Theorem 9 -3: In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent. List all pairs of congruent arcs in the diagram to the right and explain how you know.
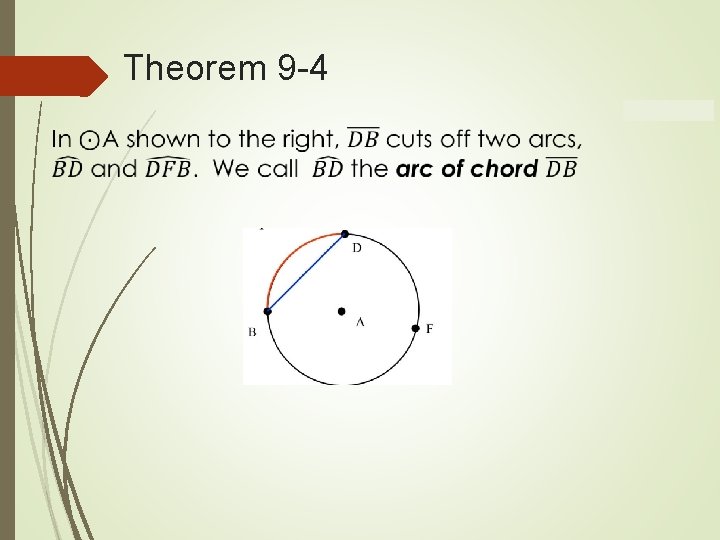
Theorem 9 -4
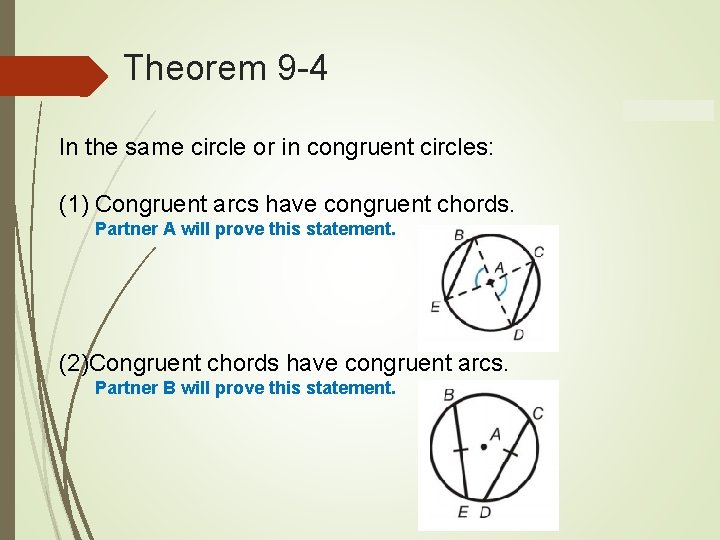
Theorem 9 -4 In the same circle or in congruent circles: (1) Congruent arcs have congruent chords. Partner A will prove this statement. (2)Congruent chords have congruent arcs. Partner B will prove this statement.
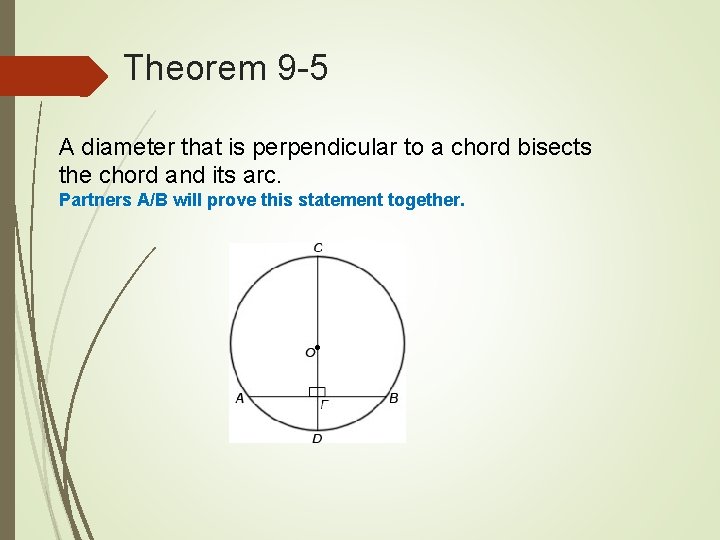
Theorem 9 -5 A diameter that is perpendicular to a chord bisects the chord and its arc. Partners A/B will prove this statement together.
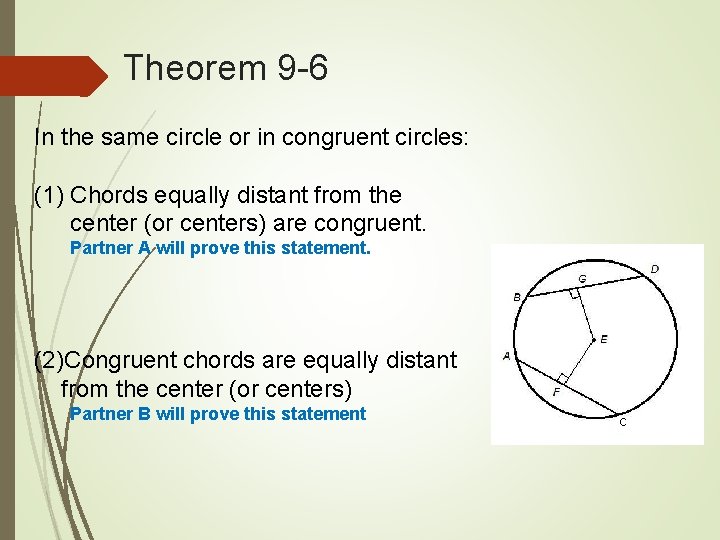
Theorem 9 -6 In the same circle or in congruent circles: (1) Chords equally distant from the center (or centers) are congruent. Partner A will prove this statement. (2)Congruent chords are equally distant from the center (or centers) Partner B will prove this statement C

Learning Log Summary LT 5 - I can apply theorems about the chords of a circle in proof and problem solving. Theorems involving chords state… The chord of an arc…

An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of the circle. The angle intercepts the arc shown in in color.
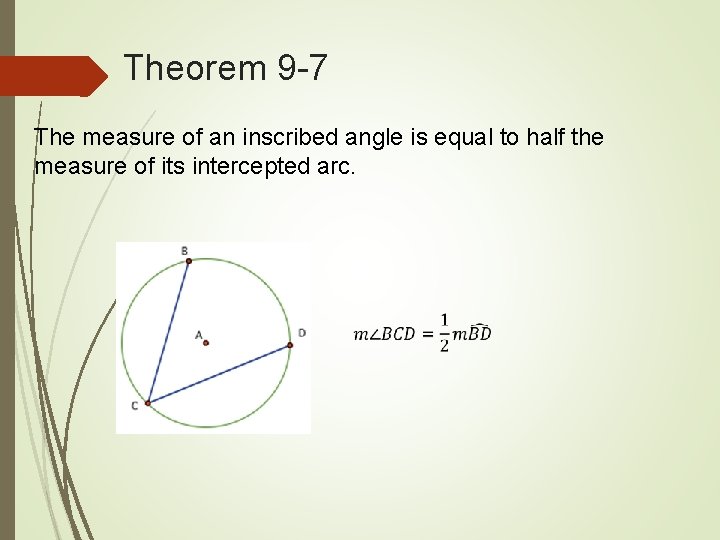
Theorem 9 -7 The measure of an inscribed angle is equal to half the measure of its intercepted arc.
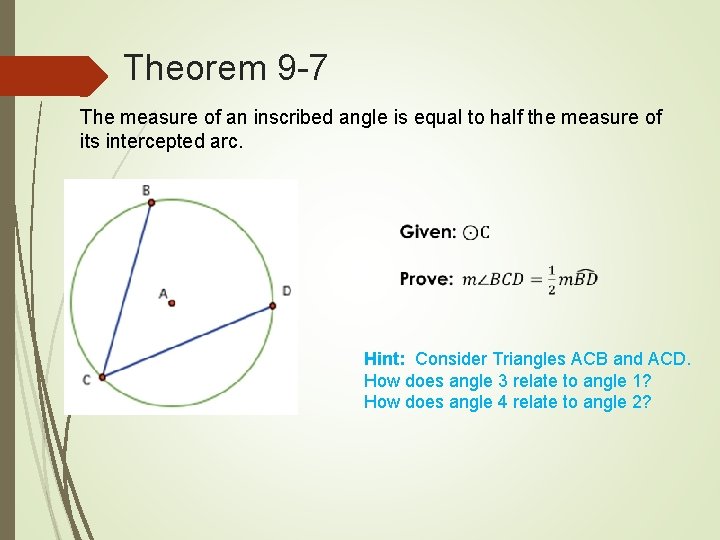
Theorem 9 -7 The measure of an inscribed angle is equal to half the measure of its intercepted arc. Hint: Consider Triangles ACB and ACD. How does angle 3 relate to angle 1? How does angle 4 relate to angle 2?
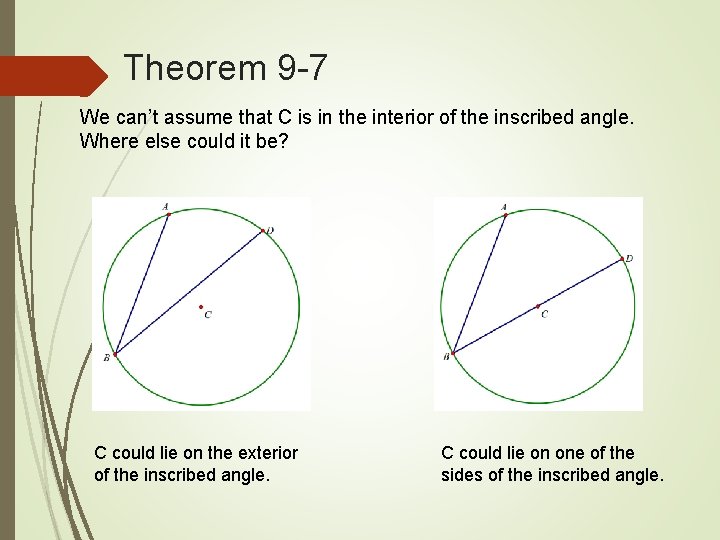
Theorem 9 -7 We can’t assume that C is in the interior of the inscribed angle. Where else could it be? C could lie on the exterior of the inscribed angle. C could lie on one of the sides of the inscribed angle.
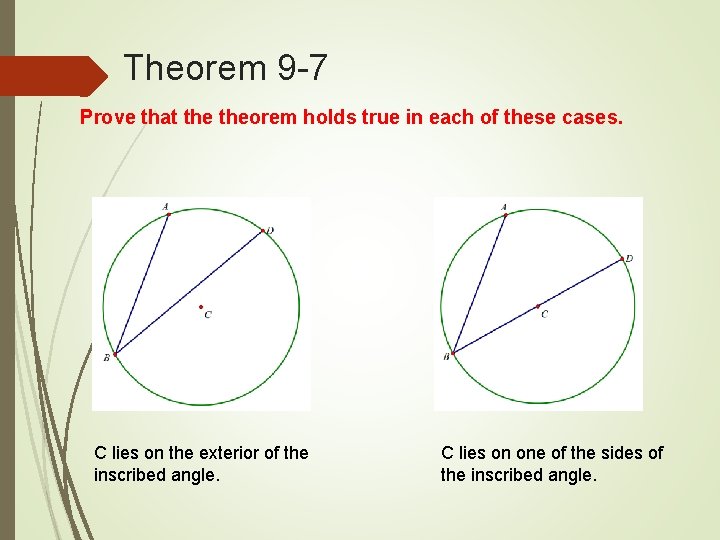
Theorem 9 -7 Prove that theorem holds true in each of these cases. C lies on the exterior of the inscribed angle. C lies on one of the sides of the inscribed angle.
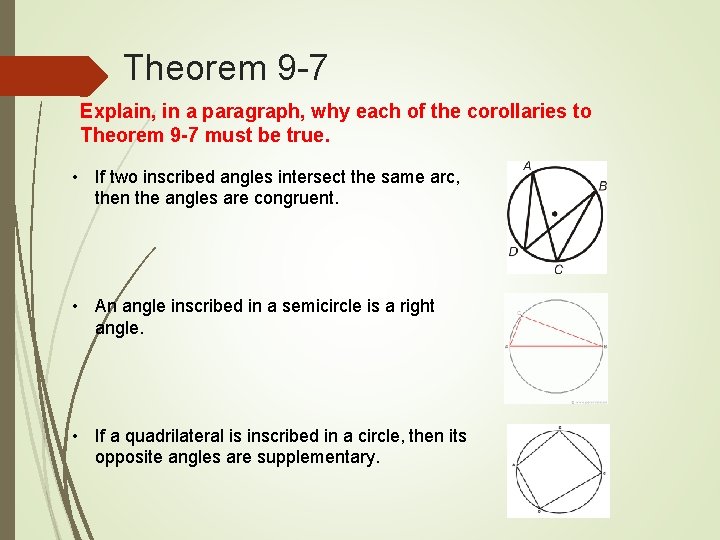
Theorem 9 -7 Explain, in a paragraph, why each of the corollaries to Theorem 9 -7 must be true. • If two inscribed angles intersect the same arc, then the angles are congruent. • An angle inscribed in a semicircle is a right angle. • If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary.
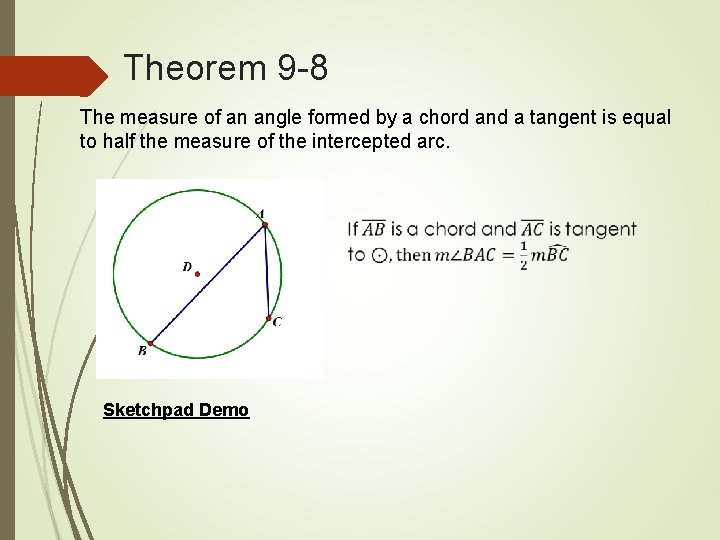
Theorem 9 -8 The measure of an angle formed by a chord and a tangent is equal to half the measure of the intercepted arc. Sketchpad Demo

Learning Log Summary LT 4 - I can prove and apply relationships between arcs, central, inscribed [interior and exterior] angles. An angle inscribed in a circle… The arc intercepted by a central angle / inscribed angle…

Quiz Overview Learning Targets: 1 - Tangents and Radii 2/3 – Proof by Contradiction 4 – Arcs/Central and Inscribed Angles 5 – Chords of a Circle 6 – Inscribed Polygons 9/10 – Tangent Constructions Theorems: 9 -1 through 9 -8

Problem Solving Circle D has center (-2, -7) and radius 7. What is the measure, in degrees, of the major arc that passes through points H(-2, 0), J(5, -7), and K(-9, -7)?
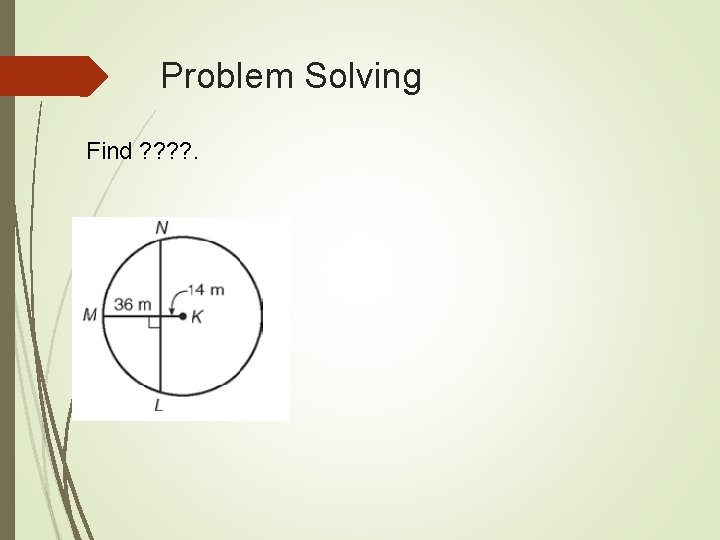
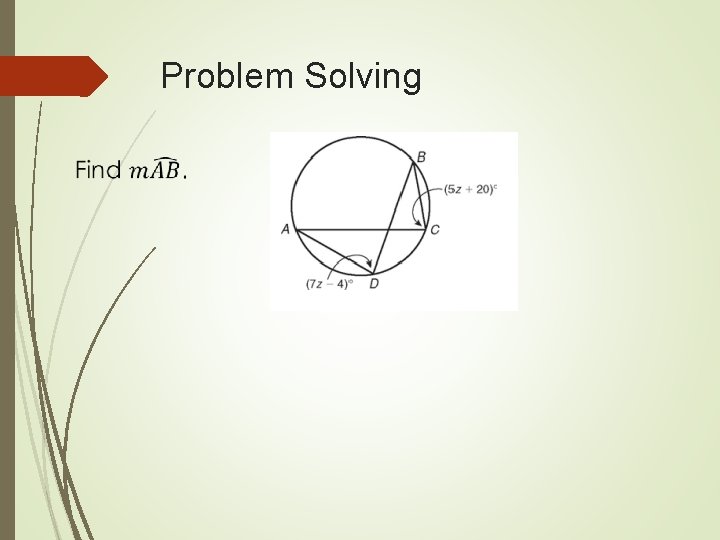
Problem Solving Find ? ? .
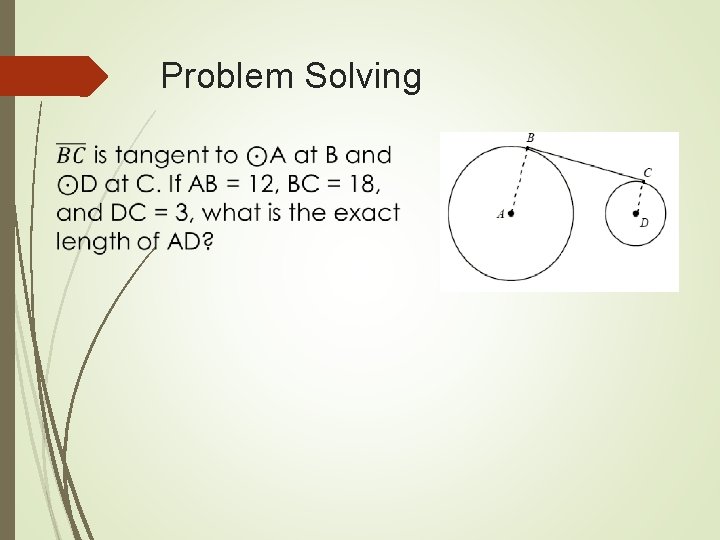
Problem Solving
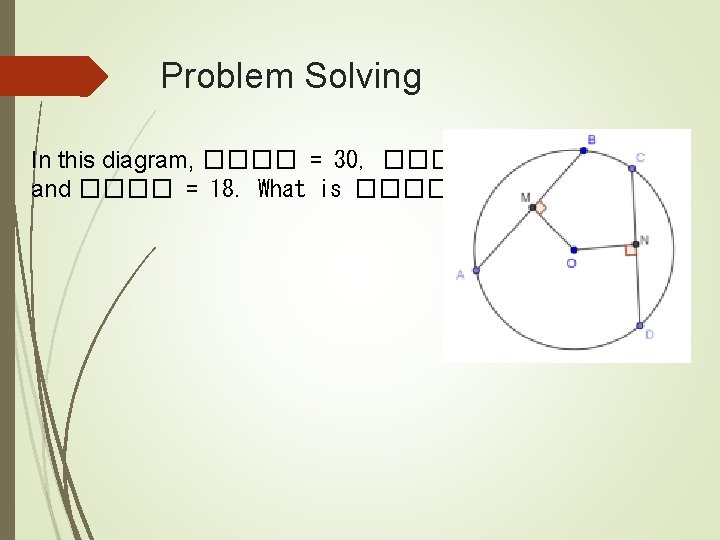
Problem Solving In this diagram, ���� = 30, ���� = 20, and ���� = 18. What is ����?
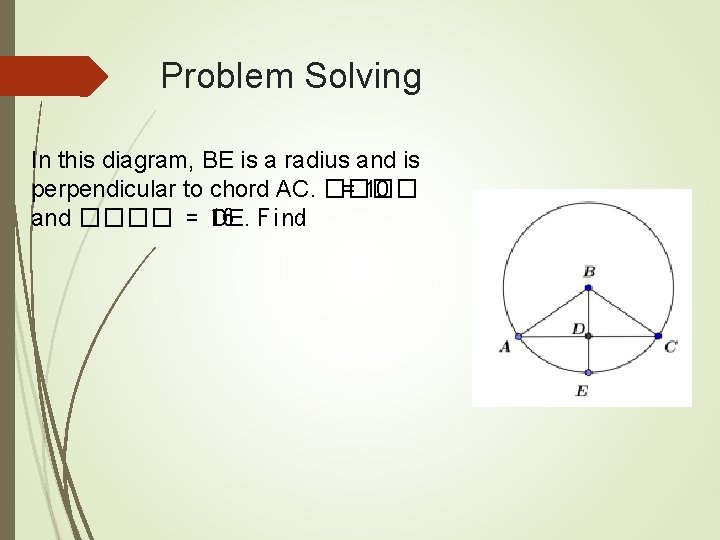
Problem Solving In this diagram, BE is a radius and is perpendicular to chord AC. ���� = 10 and ���� = 16. DE. Find

Problem Solving
Problem Solving
- Slides: 50