Circle Theorems L O All pupils can label

Circle Theorems L. O. • All pupils can label ALL the parts of a circle • All pupils know what is so special about a circle • All pupils can recognise the circle theorems • Some pupils can prove the circle theorems

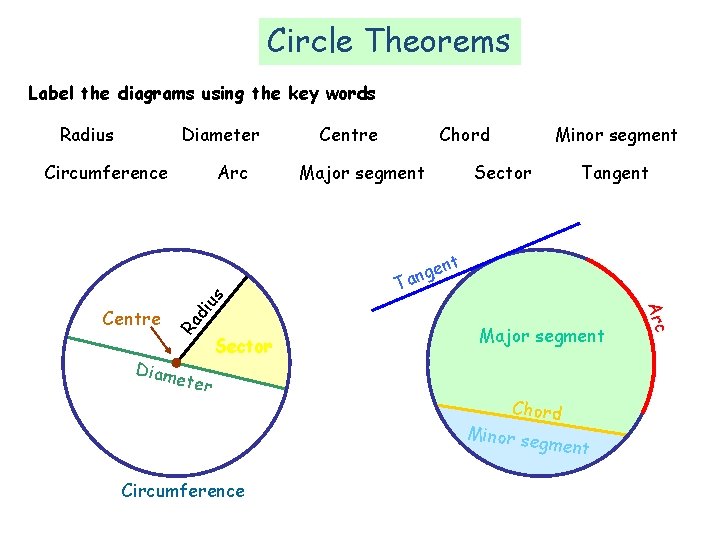
Circle Theorems Label the diagrams using the key words Diameter Radius Circumference Arc Centre Chord Major segment Minor segment Sector Tangent di Ra Diam eter Sector Major segment Chord Minor se gment Circumference Arc Centre us t gen n a T

Circle Theorems L. O. • All pupils can label ALL the parts of a circle • All pupils know what is so special about a circle • All pupils can recognise the circle theorems • Some pupils can prove the circle theorems

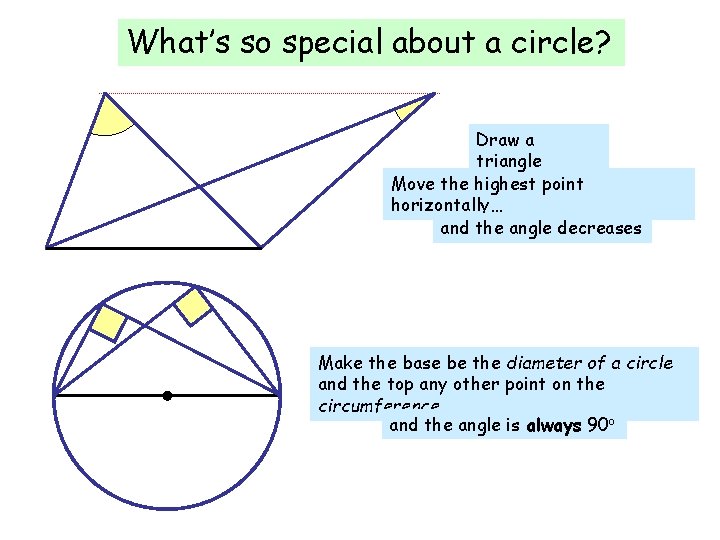
What’s so special about a circle? Draw a triangle Move the highest point horizontally… and the angle decreases Make the base be the diameter of a circle and the top any other point on the circumference… and the angle is always 90 o

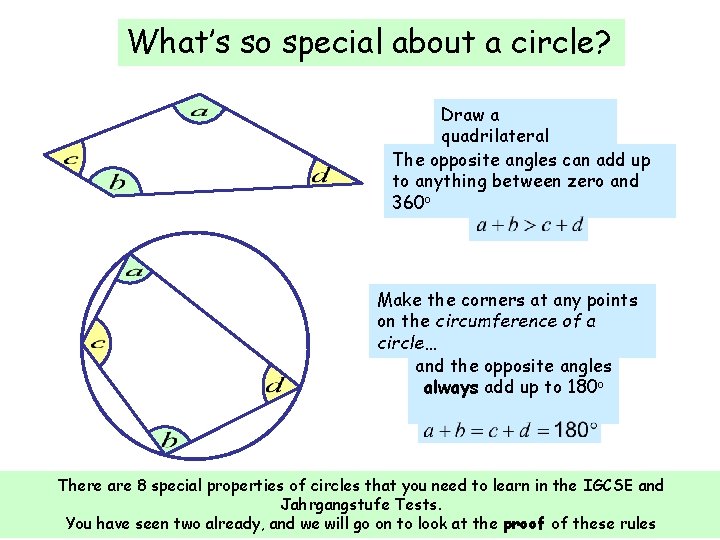
What’s so special about a circle? Draw a quadrilateral The opposite angles can add up to anything between zero and 360 o Make the corners at any points on the circumference of a circle… and the opposite angles always add up to 180 o There are 8 special properties of circles that you need to learn in the IGCSE and Jahrgangstufe Tests. You have seen two already, and we will go on to look at the proof of these rules

Circle Theorems L. O. • All pupils can label ALL the parts of a circle • All pupils know what is so special about a circle • All pupils can recognise the circle theorems • Some pupils can prove the circle theorems

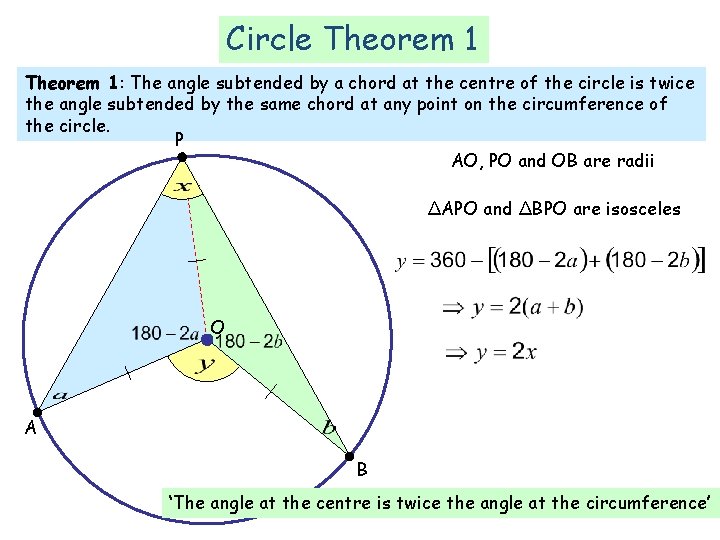
Circle Theorem 1: The angle subtended by a chord at the centre of the circle is twice the angle subtended by the same chord at any point on the circumference of the circle. P AO, PO and OB are radii ΔAPO and ΔBPO are isosceles O A B ‘The angle at the centre is twice the angle at the circumference’

Circle Theorem 1 – Some Questions

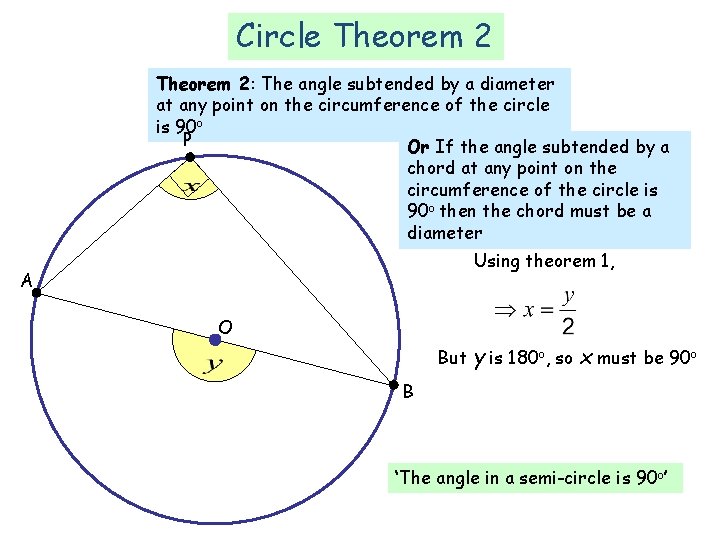
Circle Theorem 2: The angle subtended by a diameter at any point on the circumference of the circle is 90 o P Or If the angle subtended by a chord at any point on the circumference of the circle is 90 o then the chord must be a diameter Using theorem 1, A O But y is 180 o, so x must be 90 o B ‘The angle in a semi-circle is 90 o’

Circle Theorem 2 – Some Questions

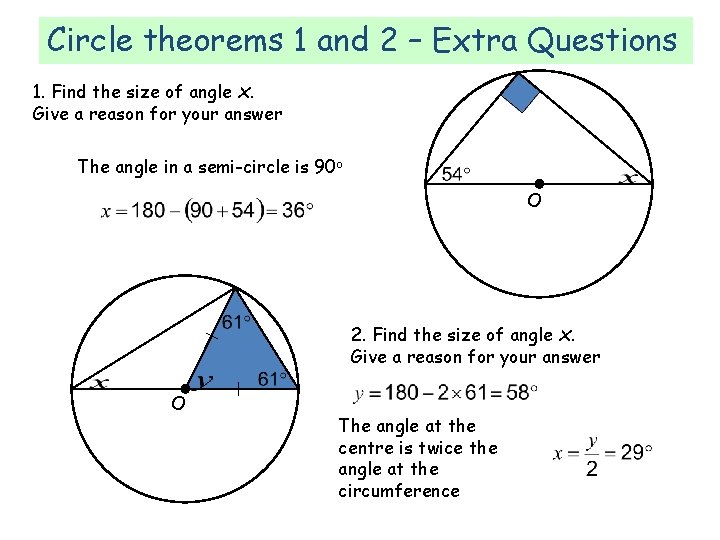
Circle theorems 1 and 2 – Extra Questions 1. Find the size of angle x. Give a reason for your answer The angle in a semi-circle is 90 o O 2. Find the size of angle x. Give a reason for your answer O The angle at the centre is twice the angle at the circumference

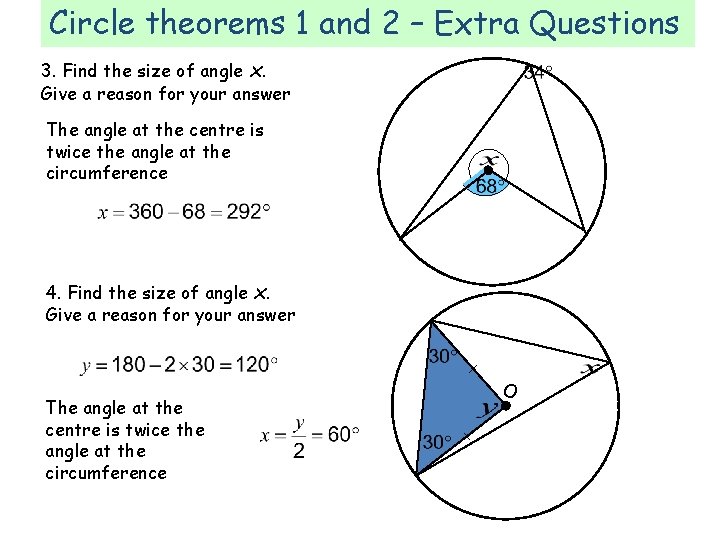
Circle theorems 1 and 2 – Extra Questions 3. Find the size of angle x. Give a reason for your answer The angle at the centre is twice the angle at the circumference 4. Find the size of angle x. Give a reason for your answer The angle at the centre is twice the angle at the circumference O

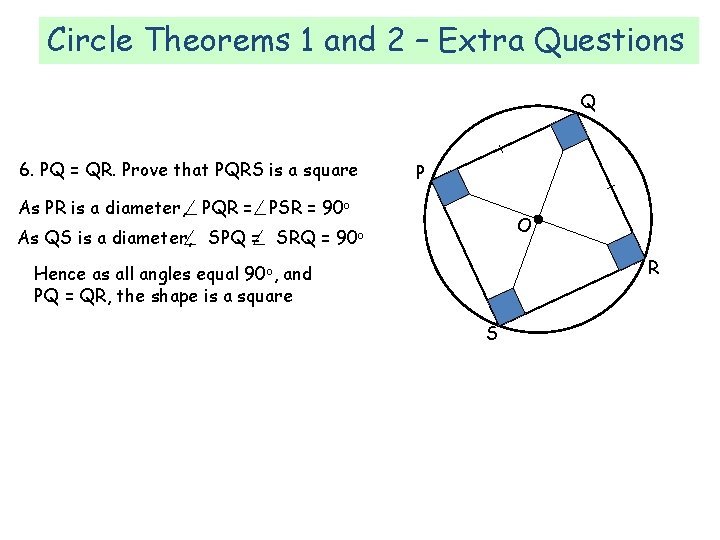
Circle Theorems 1 and 2 – Extra Questions Q 6. PQ = QR. Prove that PQRS is a square P As PR is a diameter, PQR = PSR = 90 o O As QS is a diameter, SPQ = SRQ = 90 o R Hence as all angles equal 90 o, and PQ = QR, the shape is a square S

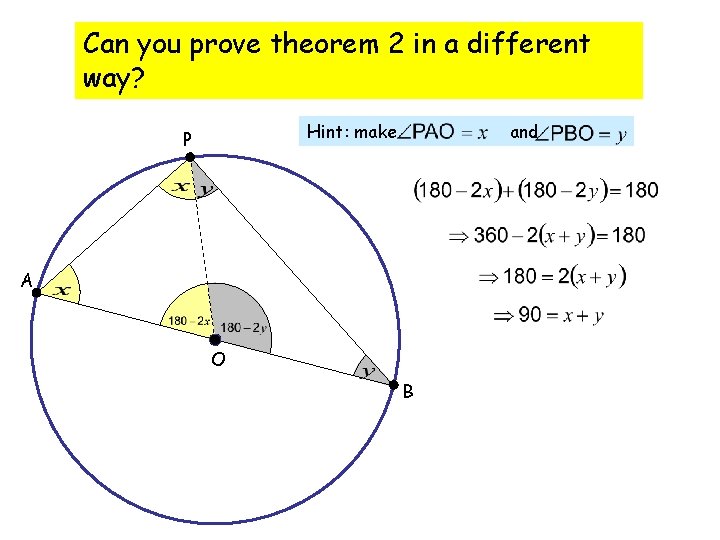
Can you prove theorem 2 in a different way? Hint: make P and A O B

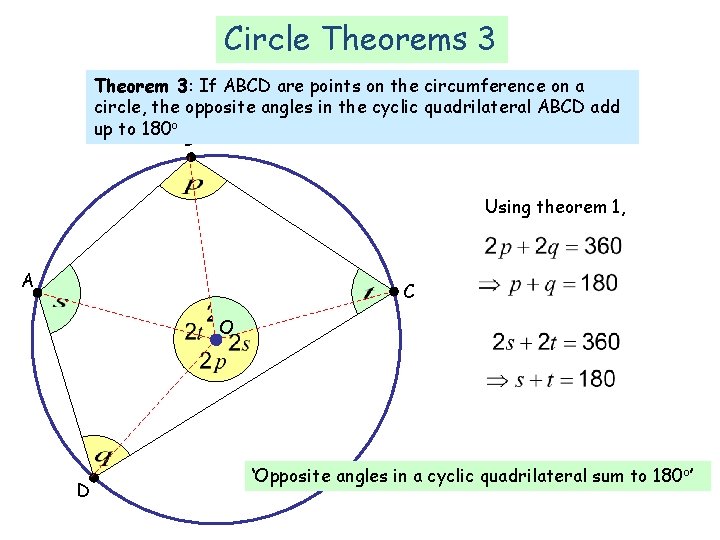
Circle Theorems 3 Theorem 3: If ABCD are points on the circumference on a circle, the opposite angles in the cyclic quadrilateral ABCD add up to 180 o B Using theorem 1, A C O D ‘Opposite angles in a cyclic quadrilateral sum to 180 o’

Circle Theorem 3 - Questions

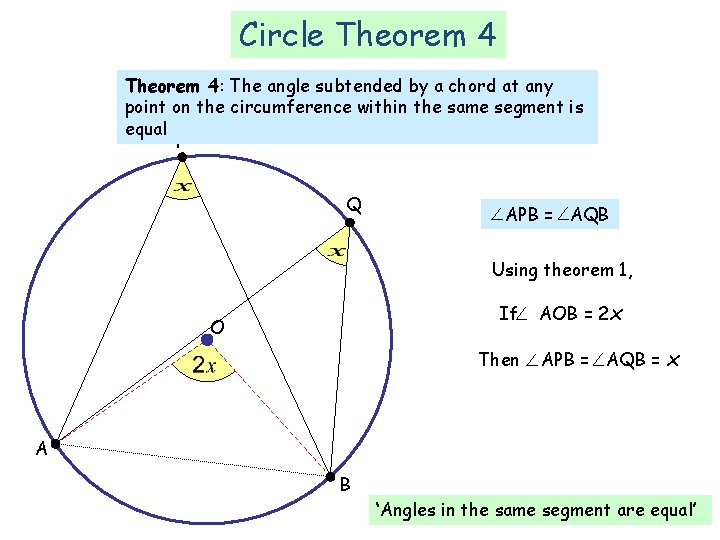
Circle Theorem 4: The angle subtended by a chord at any point on the circumference within the same segment is equal P Q APB = AQB Using theorem 1, If O Then AOB = 2 x APB = AQB = x A B ‘Angles in the same segment are equal’

Circle Theorem 4 - Questions

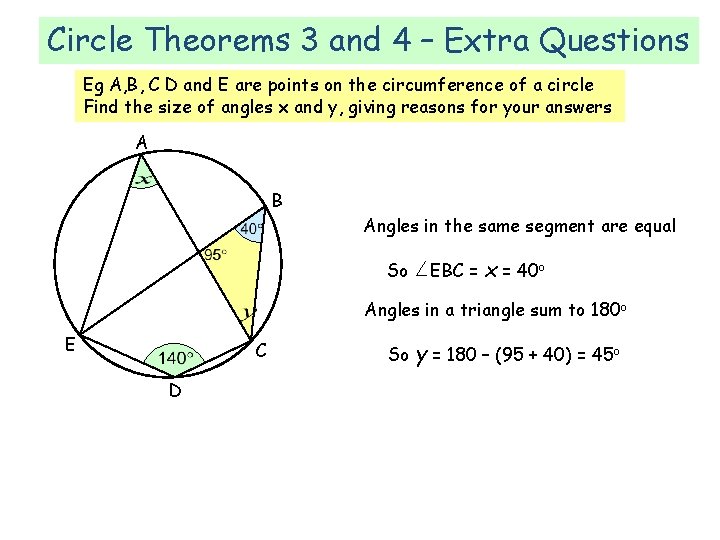
Circle Theorems 3 and 4 – Extra Questions Eg A, B, C D and E are points on the circumference of a circle Find the size of angles x and y, giving reasons for your answers A B Angles in the same segment are equal So EBC = x = 40 o Angles in a triangle sum to 180 o E C D So y = 180 – (95 + 40) = 45 o

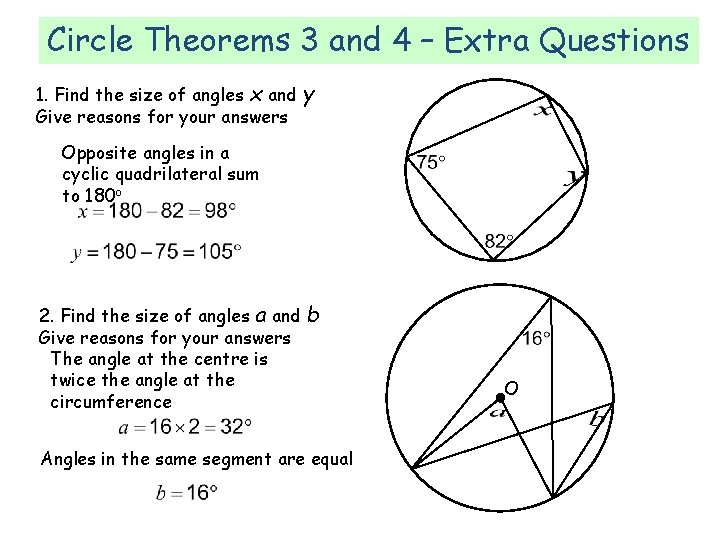
Circle Theorems 3 and 4 – Extra Questions 1. Find the size of angles x and Give reasons for your answers y Opposite angles in a cyclic quadrilateral sum to 180 o 2. Find the size of angles a and Give reasons for your answers The angle at the centre is twice the angle at the circumference b Angles in the same segment are equal O

Circle Theorems 3 and 4 – Extra Questions 6. Find the size of angle x Imagine point P on the circumference The angle at the centre is twice the angle at the circumference, so angle at P is 55 o Opposite angles in a cyclic quadrilateral sum to 180 o O P

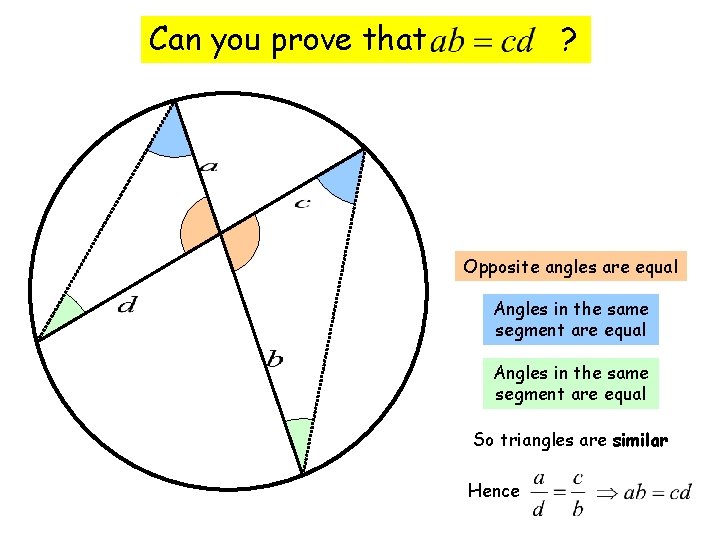
Can you prove that ? Opposite angles are equal Angles in the same segment are equal So triangles are similar Hence

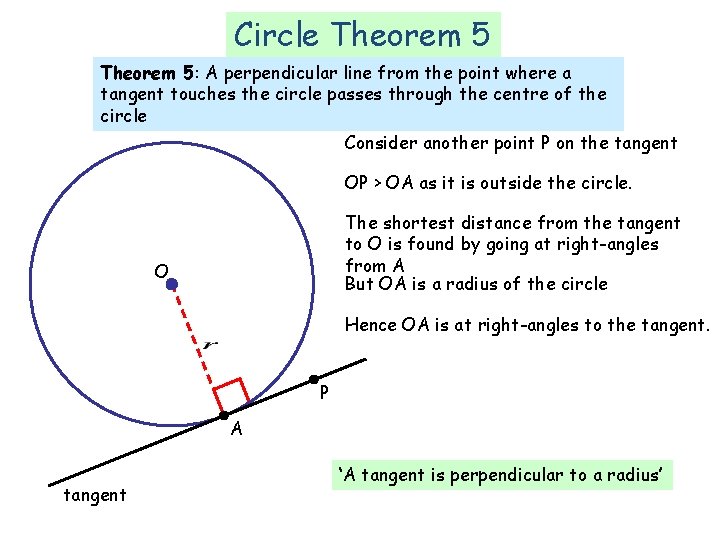
Circle Theorem 5: A perpendicular line from the point where a tangent touches the circle passes through the centre of the circle Consider another point P on the tangent OP > OA as it is outside the circle. The shortest distance from the tangent to O is found by going at right-angles from A But OA is a radius of the circle O Hence OA is at right-angles to the tangent. P A tangent ‘A tangent is perpendicular to a radius’

Circle Theorem 5 - Questions

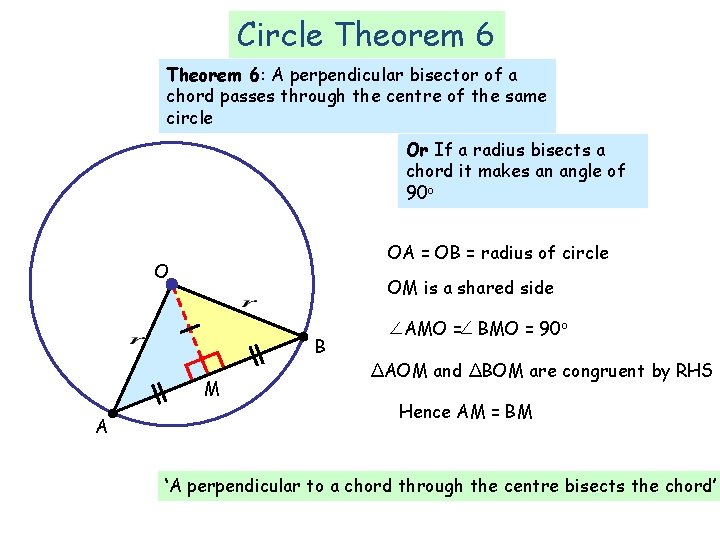
Circle Theorem 6: A perpendicular bisector of a chord passes through the centre of the same circle Or If a radius bisects a chord it makes an angle of 90 o OA = OB = radius of circle O OM is a shared side B M A AMO = BMO = 90 o ΔAOM and ΔBOM are congruent by RHS Hence AM = BM ‘A perpendicular to a chord through the centre bisects the chord’

Circle Theorem 6 - Questions

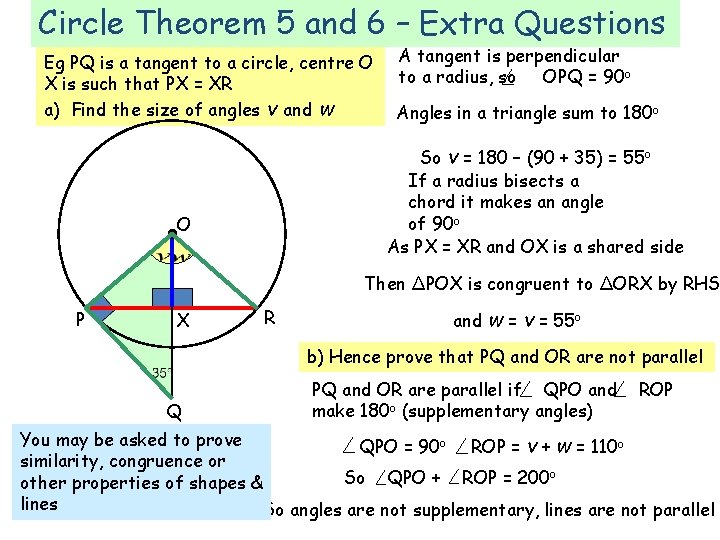
Circle Theorem 5 and 6 – Extra Questions Eg PQ is a tangent to a circle, centre O X is such that PX = XR a) Find the size of angles v and w A tangent is perpendicular to a radius, so OPQ = 90 o Angles in a triangle sum to 180 o So v = 180 – (90 + 35) = 55 o If a radius bisects a chord it makes an angle of 90 o As PX = XR and OX is a shared side O Then ΔPOX is congruent to ΔORX by RHS P X R and w = v = 55 o b) Hence prove that PQ and OR are not parallel Q PQ and OR are parallel if QPO and make 180 o (supplementary angles) ROP You may be asked to prove QPO = 90 o ROP = v + w = 110 o similarity, congruence or So QPO + ROP = 200 o other properties of shapes & lines So angles are not supplementary, lines are not parallel

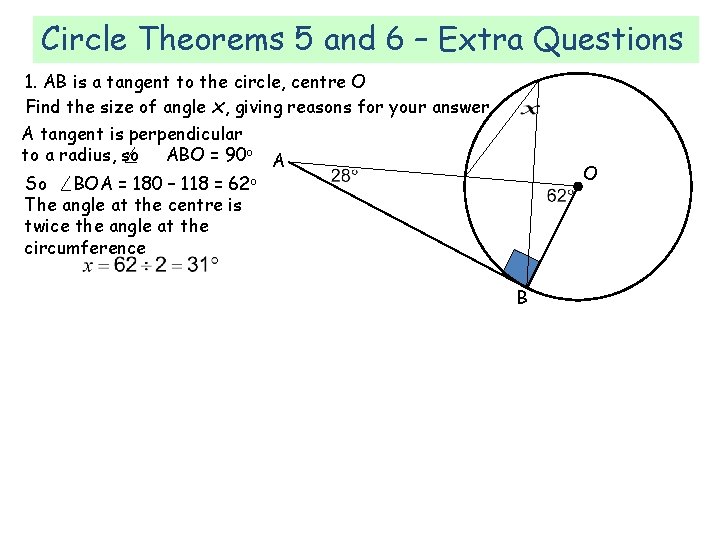
Circle Theorems 5 and 6 – Extra Questions 1. AB is a tangent to the circle, centre O Find the size of angle x, giving reasons for your answer A tangent is perpendicular to a radius, so ABO = 90 o A So BOA = 180 – 118 = 62 o The angle at the centre is twice the angle at the circumference O B

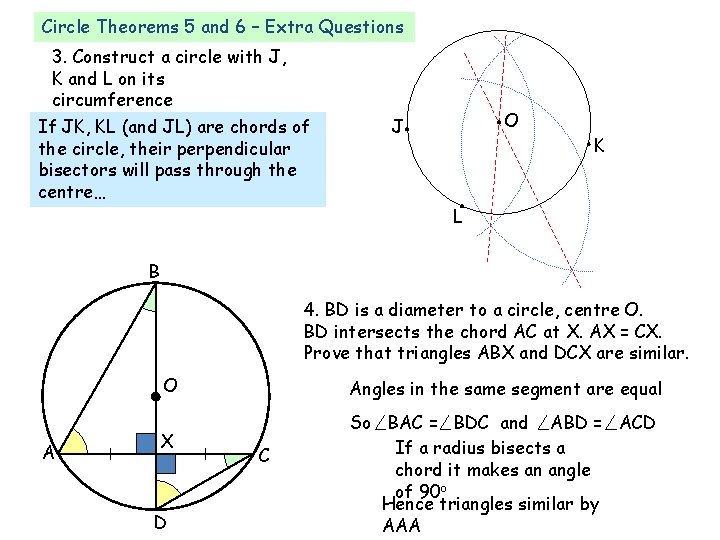
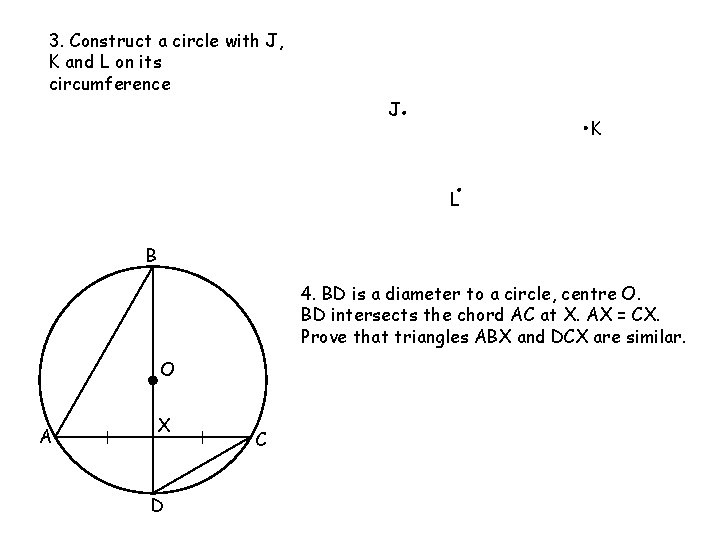
Circle Theorems 5 and 6 – Extra Questions 3. Construct a circle with J, K and L on its circumference If JK, KL (and JL) are chords of the circle, their perpendicular bisectors will pass through the centre… O J K L B 4. BD is a diameter to a circle, centre O. BD intersects the chord AC at X. AX = CX. Prove that triangles ABX and DCX are similar. O A X D Angles in the same segment are equal C So BAC = BDC and ABD = ACD If a radius bisects a chord it makes an angle of 90 o Hence triangles similar by AAA

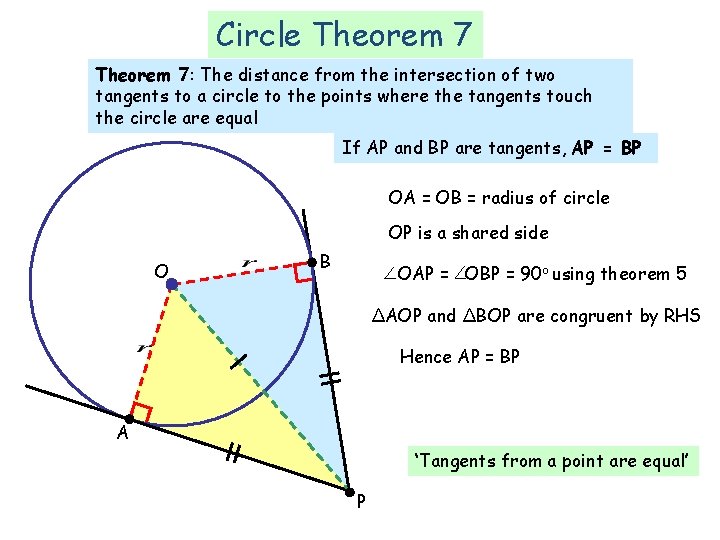
Circle Theorem 7: The distance from the intersection of two tangents to a circle to the points where the tangents touch the circle are equal If AP and BP are tangents, AP = BP OA = OB = radius of circle OP is a shared side O B OAP = OBP = 90 o using theorem 5 ΔAOP and ΔBOP are congruent by RHS Hence AP = BP A ‘Tangents from a point are equal’ P

Circle Theorem 7 - Questions

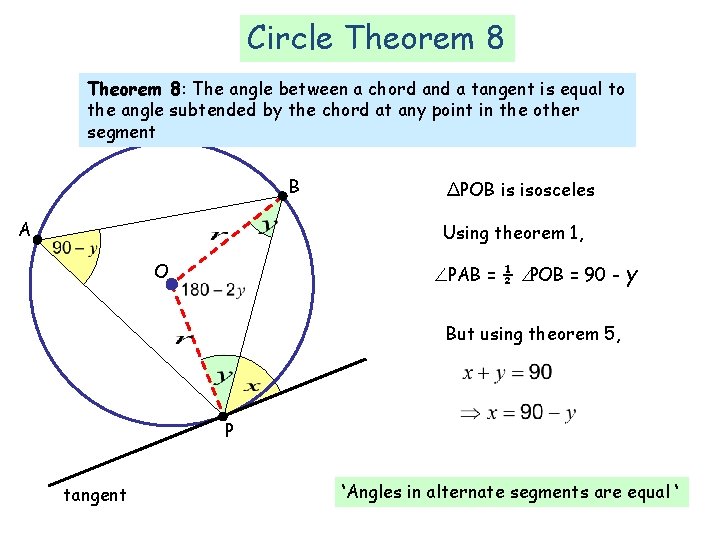
Circle Theorem 8: The angle between a chord and a tangent is equal to the angle subtended by the chord at any point in the other segment B A ΔPOB is isosceles Using theorem 1, O PAB = ½ POB = 90 - y But using theorem 5, P tangent ‘Angles in alternate segments are equal ‘

Circle Theorem 8 - Questions

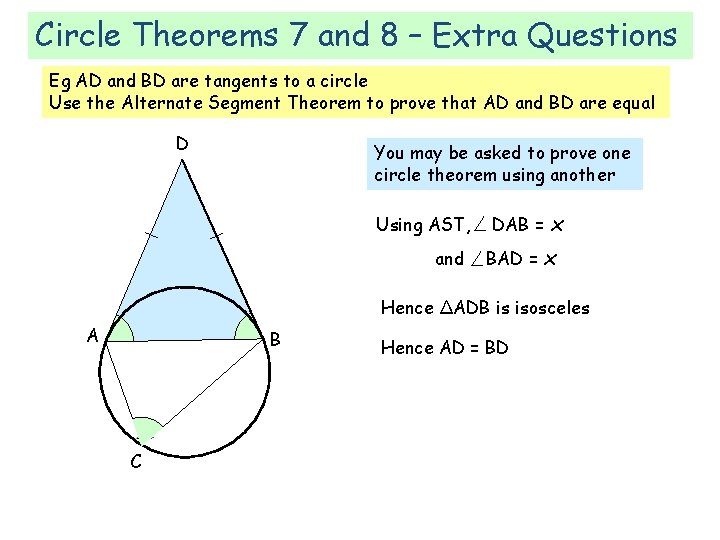
Circle Theorems 7 and 8 – Extra Questions Eg AD and BD are tangents to a circle Use the Alternate Segment Theorem to prove that AD and BD are equal D You may be asked to prove one circle theorem using another Using AST, and DAB = BAD = x x Hence ΔADB is isosceles A B C Hence AD = BD

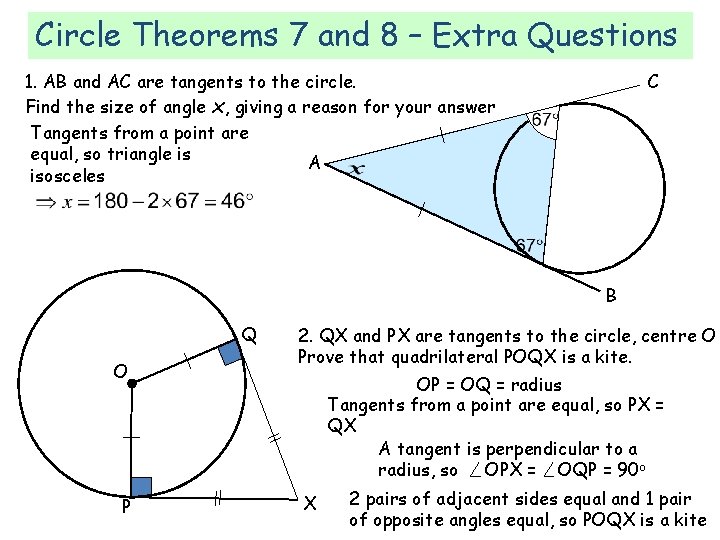
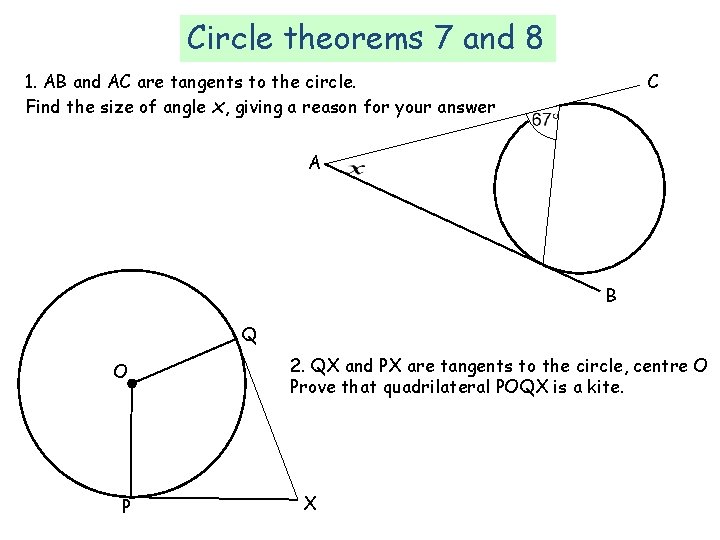
Circle Theorems 7 and 8 – Extra Questions 1. AB and AC are tangents to the circle. Find the size of angle x, giving a reason for your answer Tangents from a point are equal, so triangle is A isosceles C B Q O P 2. QX and PX are tangents to the circle, centre O Prove that quadrilateral POQX is a kite. OP = OQ = radius Tangents from a point are equal, so PX = QX A tangent is perpendicular to a radius, so OPX = OQP = 90 o X 2 pairs of adjacent sides equal and 1 pair of opposite angles equal, so POQX is a kite

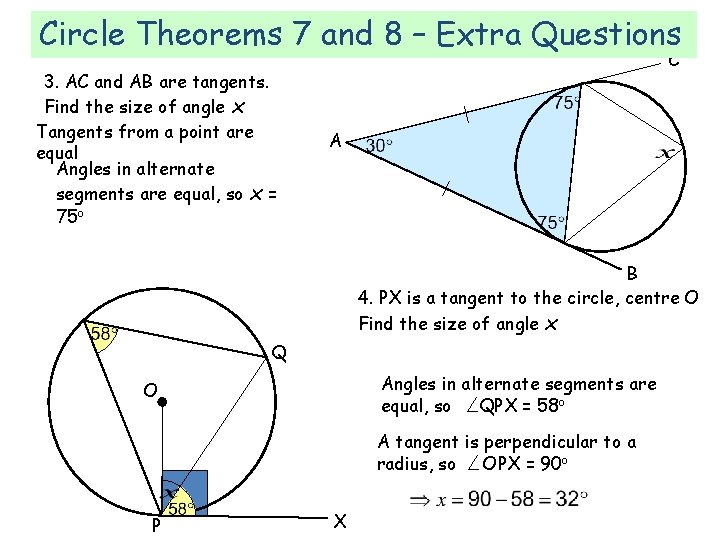
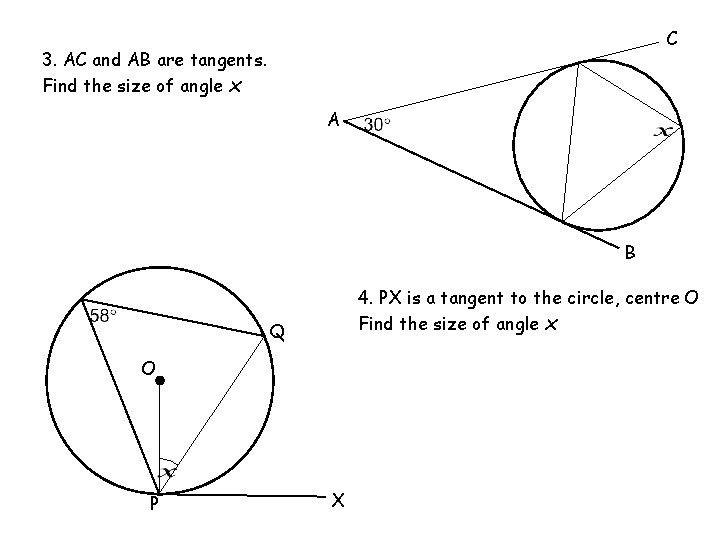
Circle Theorems 7 and 8 – Extra Questions 3. AC and AB are tangents. Find the size of angle x Tangents from a point are equal Angles in alternate segments are equal, so x = 75 o C A B 4. PX is a tangent to the circle, centre O Find the size of angle x Q Angles in alternate segments are equal, so QPX = 58 o O A tangent is perpendicular to a radius, so OPX = 90 o P X

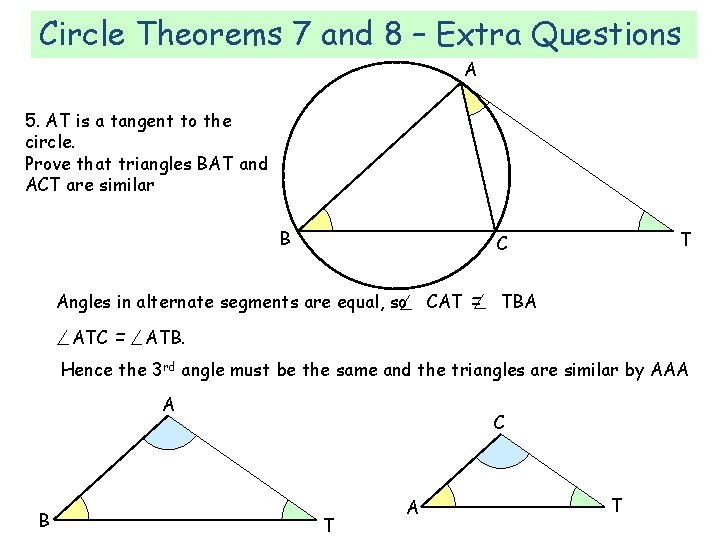
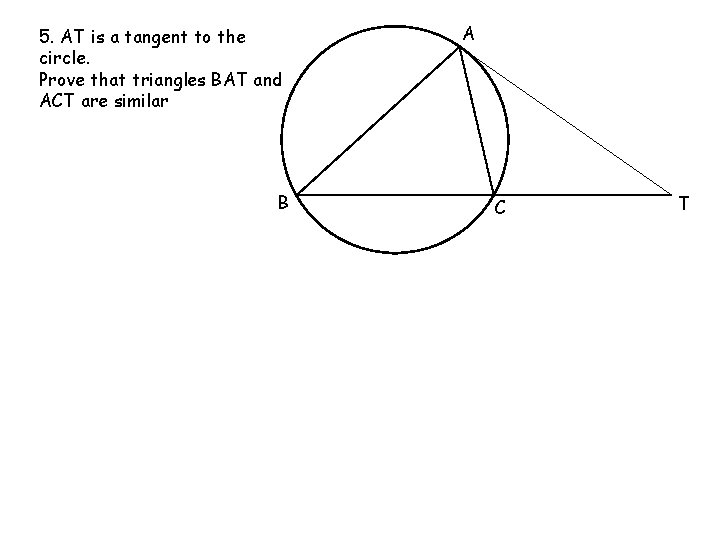
Circle Theorems 7 and 8 – Extra Questions A 5. AT is a tangent to the circle. Prove that triangles BAT and ACT are similar B Angles in alternate segments are equal, so ATC = ATB T C CAT = TBA 22 Hence the 3 rd angle must be the same and the triangles are similar by AAA A B C T A T

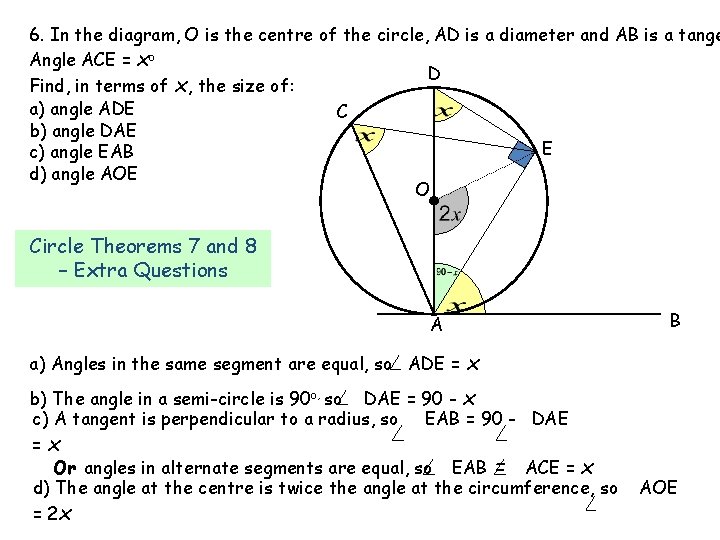
6. In the diagram, O is the centre of the circle, AD is a diameter and AB is a tange Angle ACE = xo D Find, in terms of x, the size of: a) angle ADE C b) angle DAE E c) angle EAB d) angle AOE O Circle Theorems 7 and 8 – Extra Questions B A a) Angles in the same segment are equal, so ADE = x b) The angle in a semi-circle is 90 o, so DAE = 90 - x c) A tangent is perpendicular to a radius, so EAB = 90 - DAE =x Or angles in alternate segments are equal, so EAB = ACE = x d) The angle at the centre is twice the angle at the circumference, so = 2 x AOE

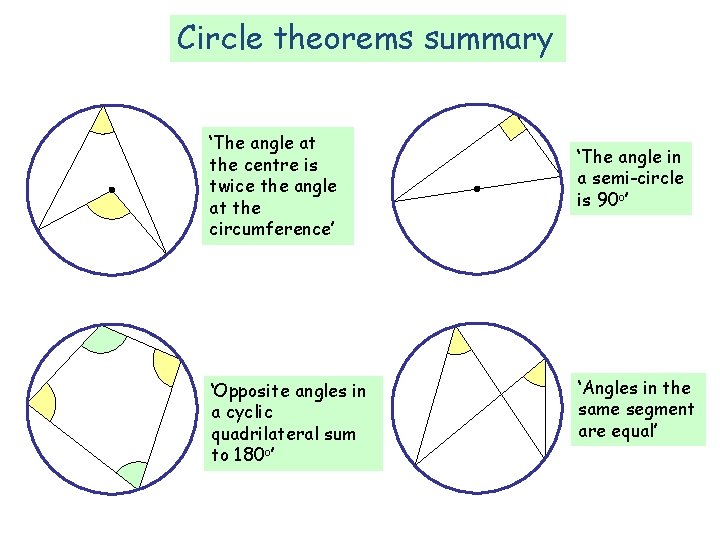
Circle theorems summary ‘The angle at the centre is twice the angle at the circumference’ ‘Opposite angles in a cyclic quadrilateral sum to 180 o’ ‘The angle in a semi-circle is 90 o’ ‘Angles in the same segment are equal’

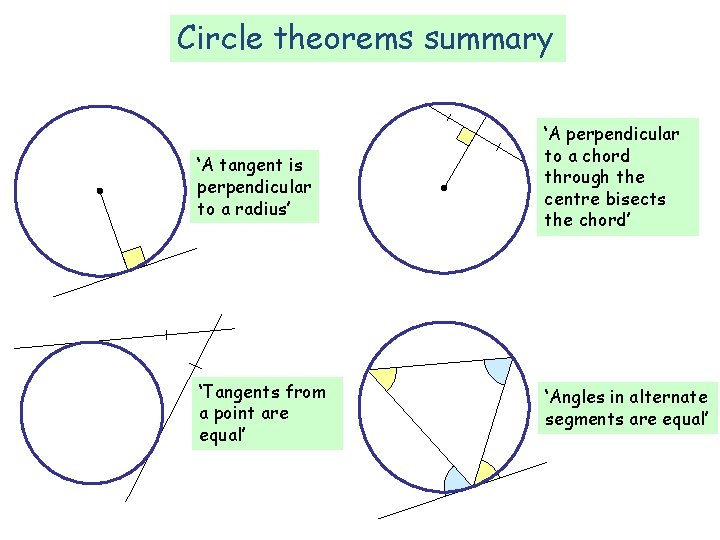
Circle theorems summary ‘A tangent is perpendicular to a radius’ ‘Tangents from a point are equal’ ‘A perpendicular to a chord through the centre bisects the chord’ ‘Angles in alternate segments are equal’

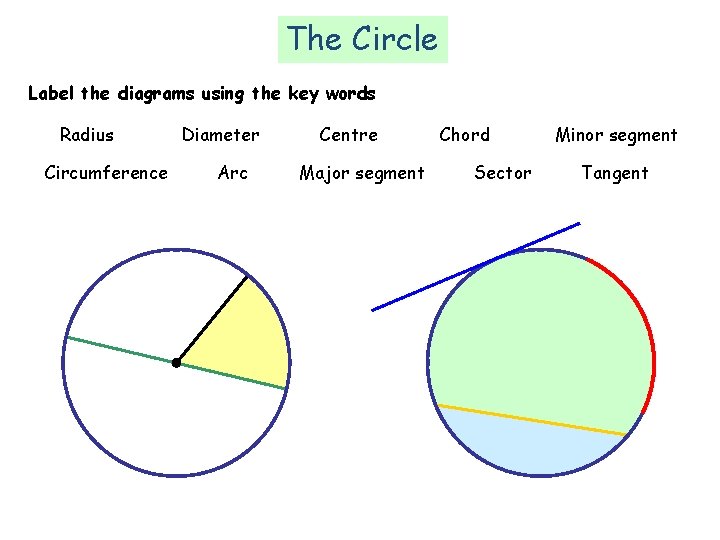
The Circle Label the diagrams using the key words Radius Circumference Diameter Arc Centre Major segment Chord Sector Minor segment Tangent

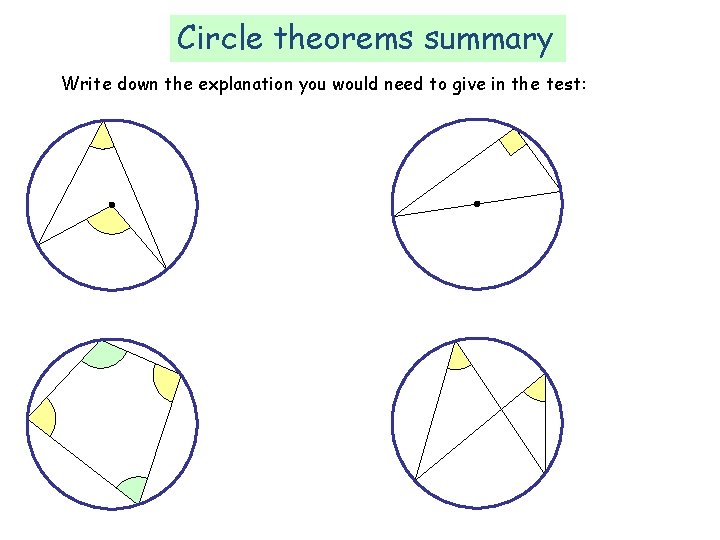
Circle theorems summary Write down the explanation you would need to give in the test:

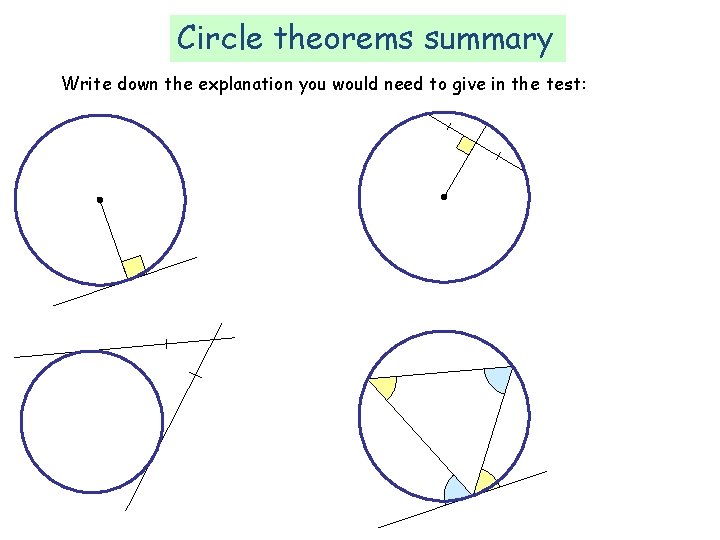
Circle theorems summary Write down the explanation you would need to give in the test:

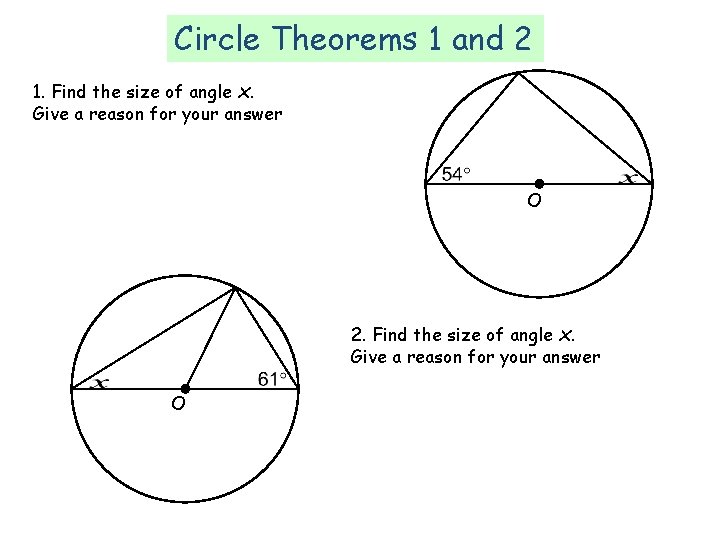
Circle Theorems 1 and 2 1. Find the size of angle x. Give a reason for your answer O 2. Find the size of angle x. Give a reason for your answer O

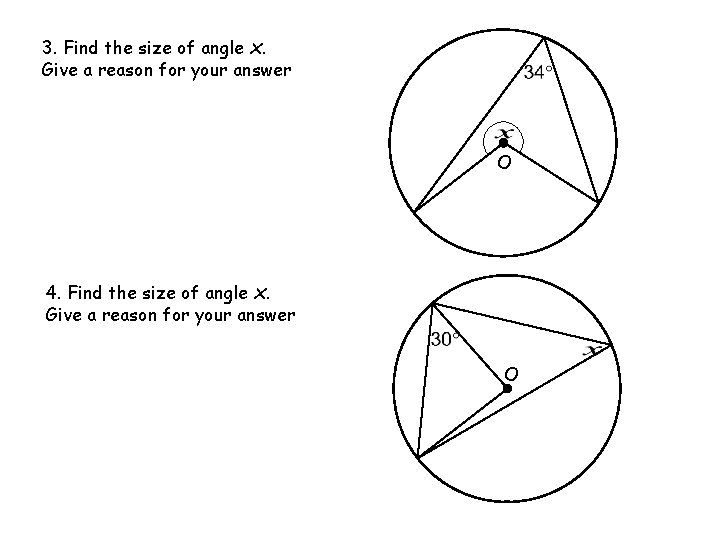
3. Find the size of angle x. Give a reason for your answer O 4. Find the size of angle x. Give a reason for your answer O

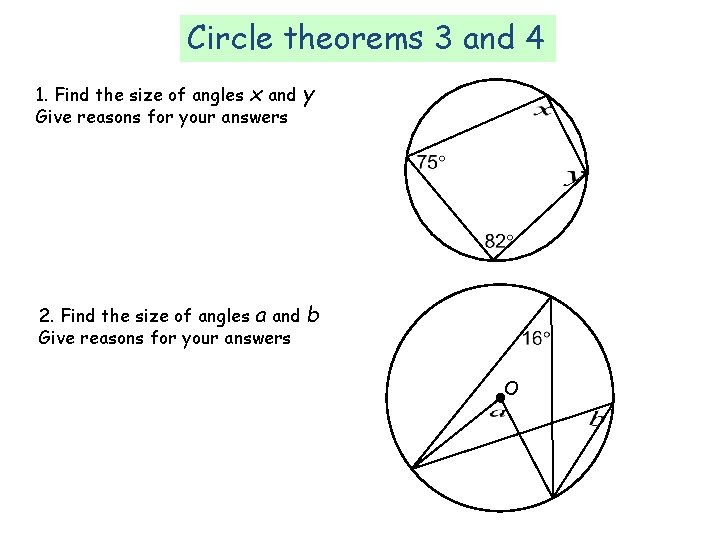
Circle theorems 3 and 4 1. Find the size of angles x and Give reasons for your answers y 2. Find the size of angles a and Give reasons for your answers b O

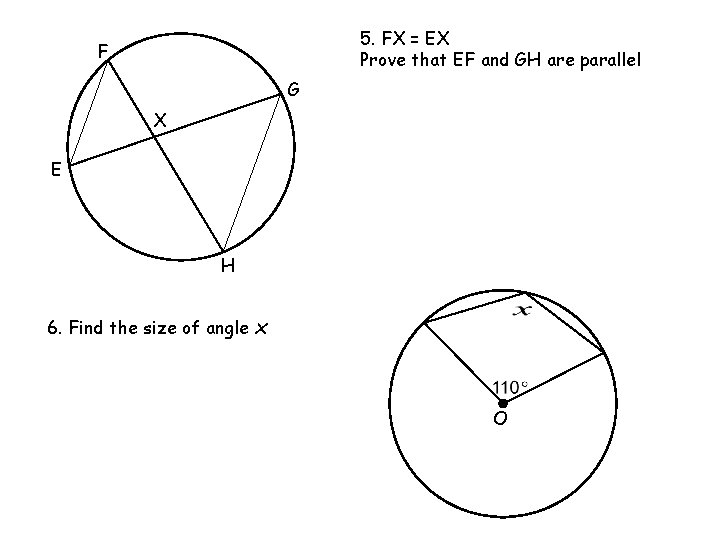
5. FX = EX Prove that EF and GH are parallel F G X E H 6. Find the size of angle x O

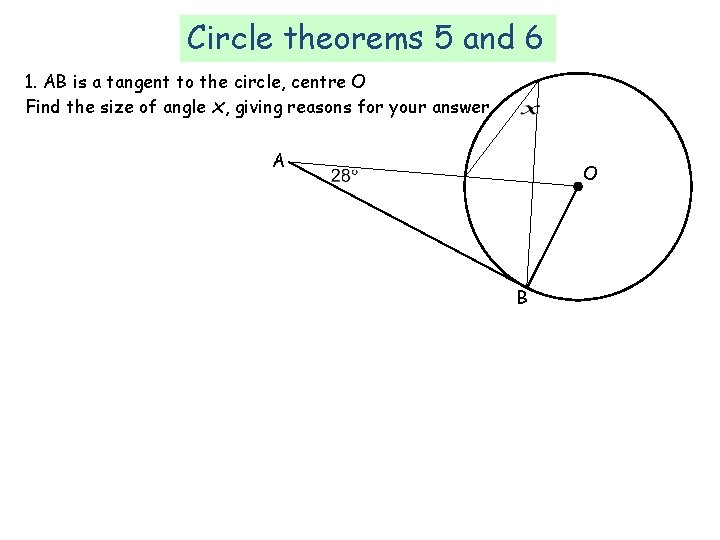
Circle theorems 5 and 6 1. AB is a tangent to the circle, centre O Find the size of angle x, giving reasons for your answer A O B

3. Construct a circle with J, K and L on its circumference J K L B 4. BD is a diameter to a circle, centre O. BD intersects the chord AC at X. AX = CX. Prove that triangles ABX and DCX are similar. O A X D C

Circle theorems 7 and 8 1. AB and AC are tangents to the circle. Find the size of angle x, giving a reason for your answer C A B Q O P 2. QX and PX are tangents to the circle, centre O Prove that quadrilateral POQX is a kite. X

C 3. AC and AB are tangents. Find the size of angle x A B 4. PX is a tangent to the circle, centre O Find the size of angle x Q O P X

5. AT is a tangent to the circle. Prove that triangles BAT and ACT are similar B A C T

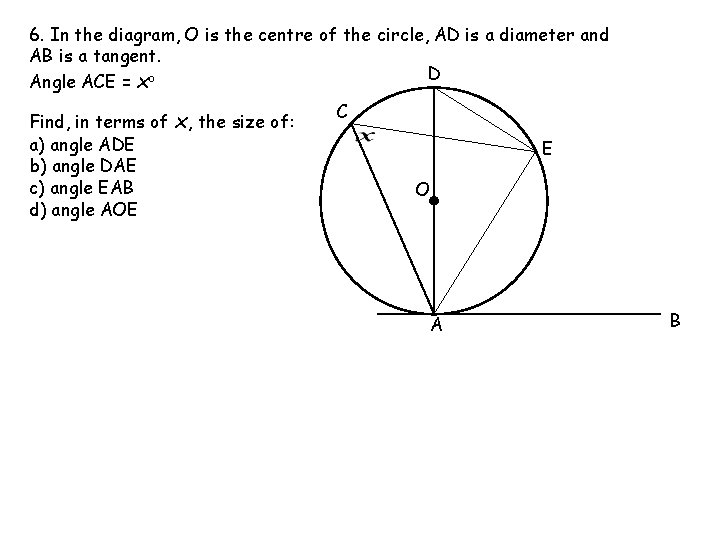
6. In the diagram, O is the centre of the circle, AD is a diameter and AB is a tangent. D Angle ACE = xo Find, in terms of a) angle ADE b) angle DAE c) angle EAB d) angle AOE x, the size of: C E O A B

Extra Hard Practice Questions. . .

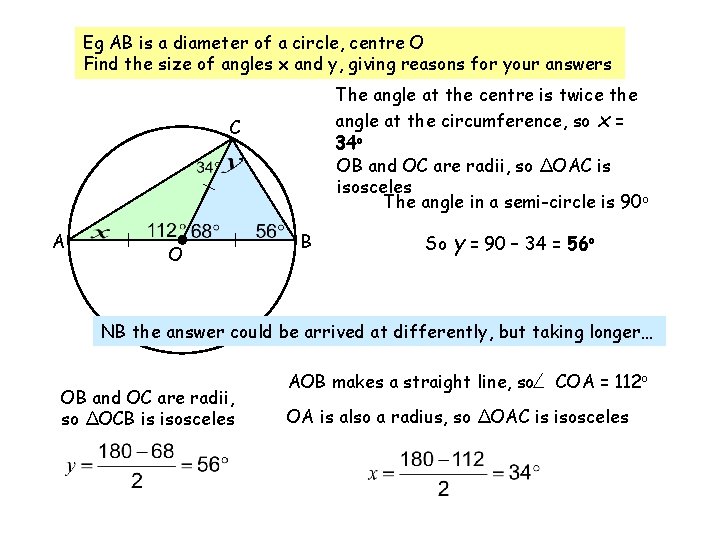
Eg AB is a diameter of a circle, centre O Find the size of angles x and y, giving reasons for your answers The angle at the centre is twice the angle at the circumference, so x = 34 o OB and OC are radii, so ΔOAC is isosceles The angle in a semi-circle is 90 o C A O B So y = 90 – 34 = 56 o NB the answer could be arrived at differently, but taking longer… OB and OC are radii, so ΔOCB is isosceles AOB makes a straight line, so COA = 112 o OA is also a radius, so ΔOAC is isosceles

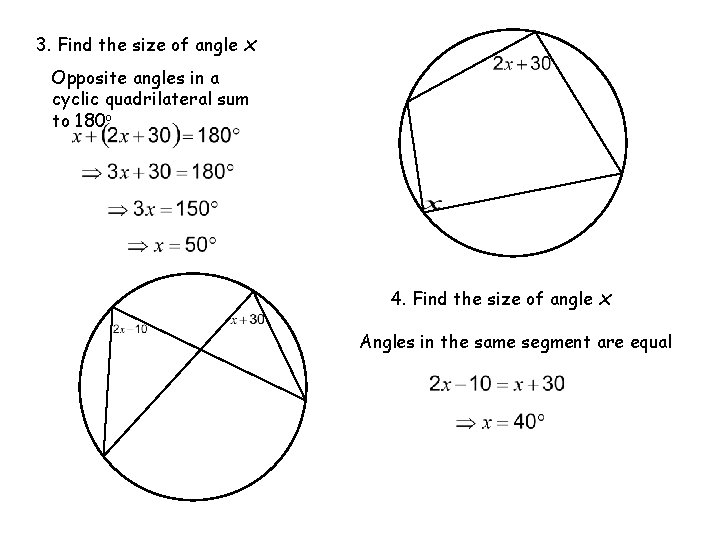
3. Find the size of angle x Opposite angles in a cyclic quadrilateral sum to 180 o 4. Find the size of angle x Angles in the same segment are equal