CIRCLE THEOREMS Circle Theorems Lesson Objectives Students will

CIRCLE THEOREMS

Circle Theorems Lesson Objectives - Students will: • Apply your knowledge of circle properties to solving problems. • Identify and apply circle theorems. Level 1 LEARN Complete “Circle Theorem” lesson Level 2 REVISE Revise Circle Properties page 408 – 409 Theorem 1 – Subtended angle at centre (p. 411), Theorem 2 – Angle in a semi-circle (p. 412), Theorem 3 – Angle in same segment (p. 415) Theorem 4 – Angles in cyclic quadratic (p. 415) (GCSE Math TEXT – red and blue) Try these: Page 410 #2, 3 , Page 413 #1, 5, 6, Page 417 #1, 2, 4, 10 Level 3 TEST Circle Theorem TEST Go to http: //www. bbc. co. uk/schools/gcsebitesize/maths/shapes/ Scroll to “Circle - Higher”, then click “Test”

Contents S 5 Circles A S 5. 1 Naming circle parts A S 5. 2 Angles in a circle A S 5. 3 Tangents and chords A S 5. 4 Circumference and arc length A S 5. 5 Areas of circles and sectors

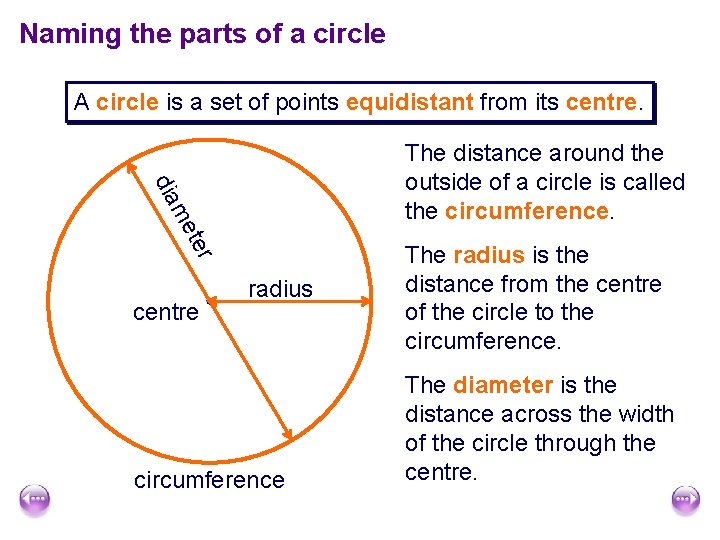
Naming the parts of a circle A circle is a set of points equidistant from its centre. ter me dia The distance around the outside of a circle is called the circumference. centre radius circumference The radius is the distance from the centre of the circle to the circumference. The diameter is the distance across the width of the circle through the centre.

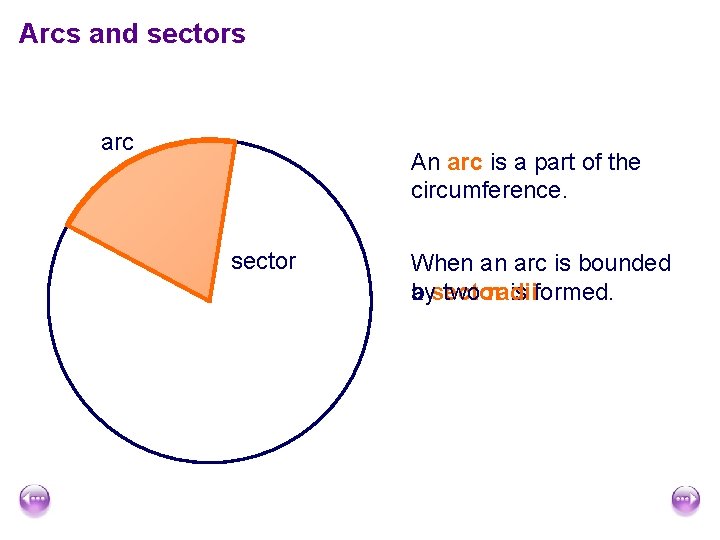
Arcs and sectors arc An arc is a part of the circumference. sector When an arc is bounded a sector by two radii is formed.

A line moving through a circle

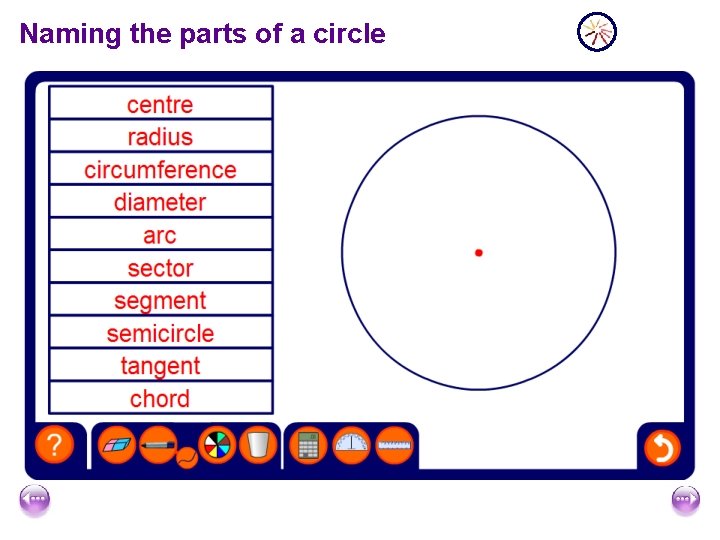
Naming the parts of a circle

Contents S 5 Circles A S 5. 1 Naming circle parts A S 5. 2 Angles in a circle A S 5. 3 Tangents and chords A S 5. 4 Circumference and arc length A S 5. 5 Areas of circles and sectors

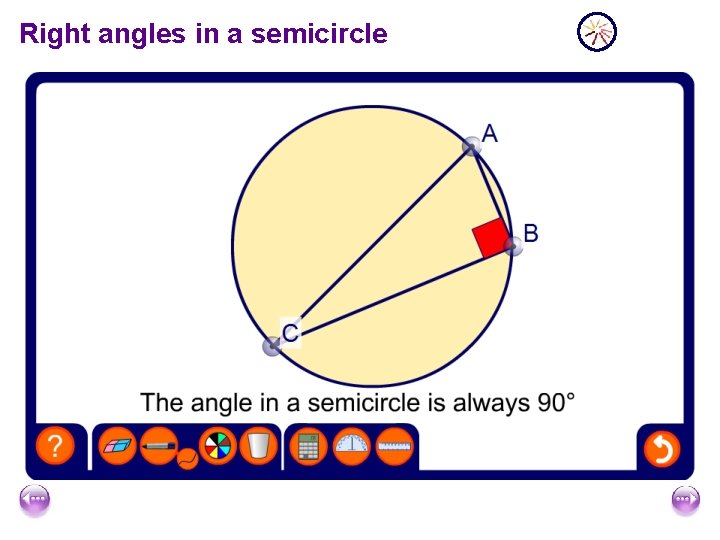
Right angles in a semicircle

Right angles in a semicircle We have just seen a demonstration that the angle in a semicircle is always a right angle. We can prove this result as follows: Draw a line from C to O. This line is a radius of the circle. C x In triangle AOC, A x O B OA = OC (both radii) So, angle OAC = angle OCA (angles at the base of an isosceles triangle) Let’s call these angles x.

Right angles in a semicircle We have just seen a demonstration that the angle in a semicircle is always a right angle. We can prove this result as follows: In triangle BOC, C OB = OC x y A y x O (both radii) So, angle OBC = angle OCB B (angles at the base of an isosceles triangle) Let’s call these angles y.

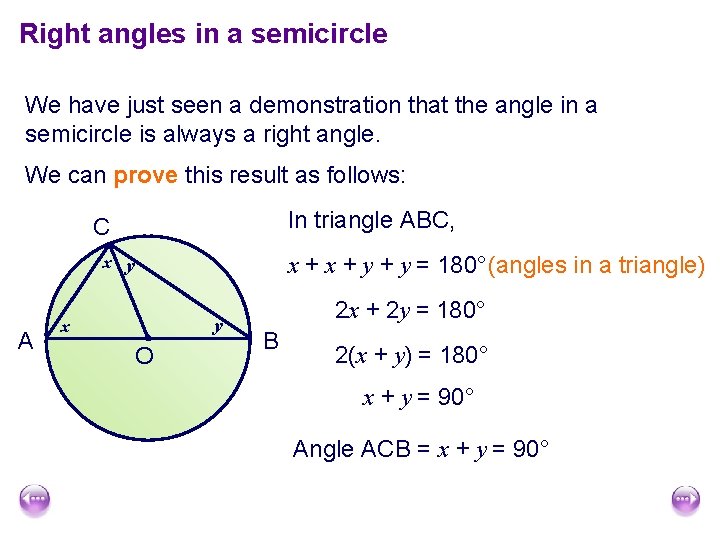
Right angles in a semicircle We have just seen a demonstration that the angle in a semicircle is always a right angle. We can prove this result as follows: In triangle ABC, C x + y + y = 180°(angles in a triangle) x y A y x O 2 x + 2 y = 180° B 2(x + y) = 180° x + y = 90° Angle ACB = x + y = 90°

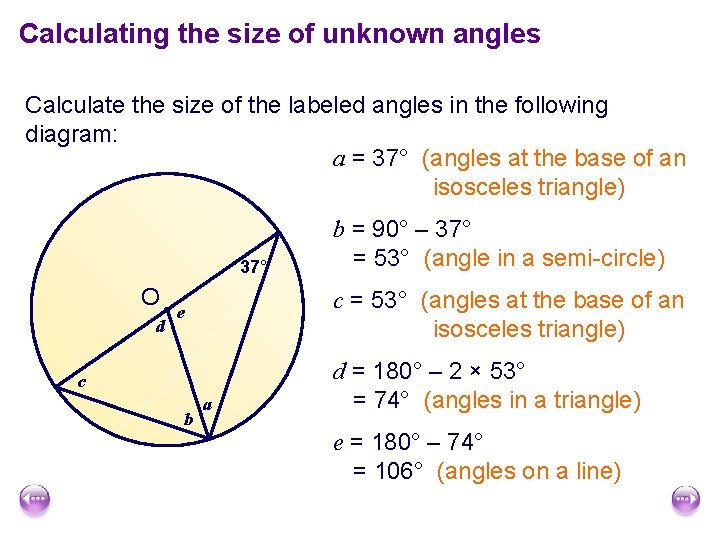
Calculating the size of unknown angles Calculate the size of the labeled angles in the following diagram: a = 37° (angles at the base of an isosceles triangle) 37° O d c = 53° (angles at the base of an isosceles triangle) e c b b = 90° – 37° = 53° (angle in a semi-circle) a d = 180° – 2 × 53° = 74° (angles in a triangle) e = 180° – 74° = 106° (angles on a line)

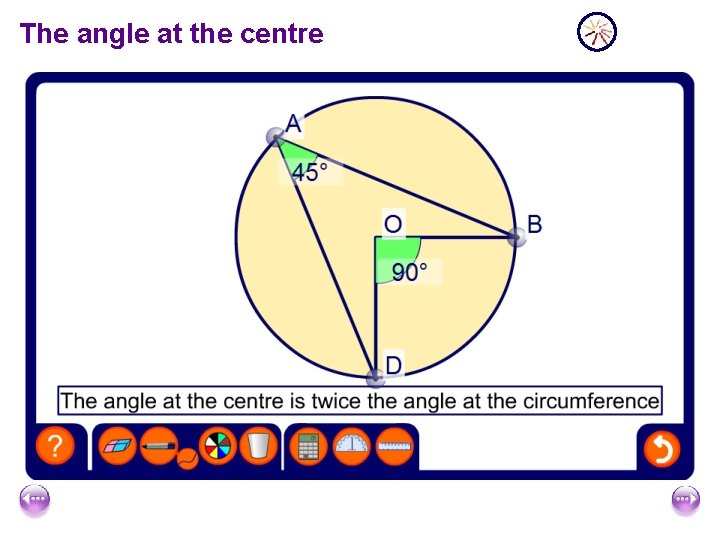
The angle at the centre

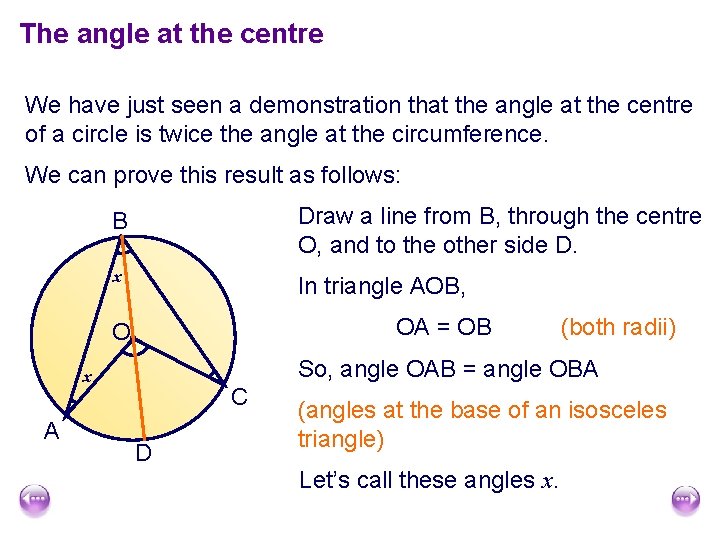
The angle at the centre We have just seen a demonstration that the angle at the centre of a circle is twice the angle at the circumference. We can prove this result as follows: B Draw a line from B, through the centre O, and to the other side D. x In triangle AOB, OA = OB O So, angle OAB = angle OBA x A (both radii) C D (angles at the base of an isosceles triangle) Let’s call these angles x.

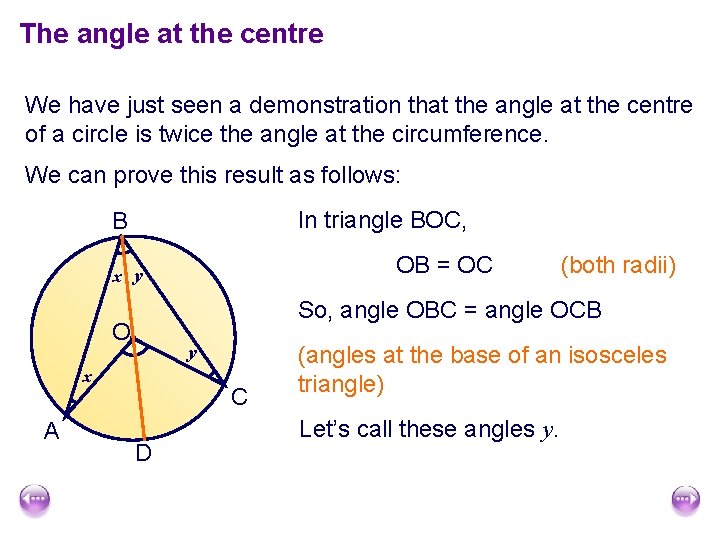
The angle at the centre We have just seen a demonstration that the angle at the centre of a circle is twice the angle at the circumference. We can prove this result as follows: In triangle BOC, B OB = OC x y So, angle OBC = angle OCB O y x A (both radii) C D (angles at the base of an isosceles triangle) Let’s call these angles y.

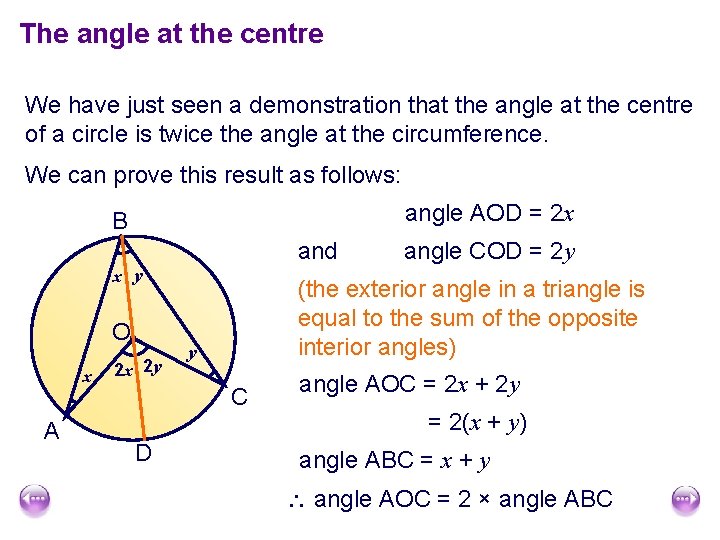
The angle at the centre We have just seen a demonstration that the angle at the centre of a circle is twice the angle at the circumference. We can prove this result as follows: angle AOD = 2 x B and x y O x A 2 x 2 y (the exterior angle in a triangle is equal to the sum of the opposite interior angles) y C D angle COD = 2 y angle AOC = 2 x + 2 y = 2(x + y) angle ABC = x + y angle AOC = 2 × angle ABC

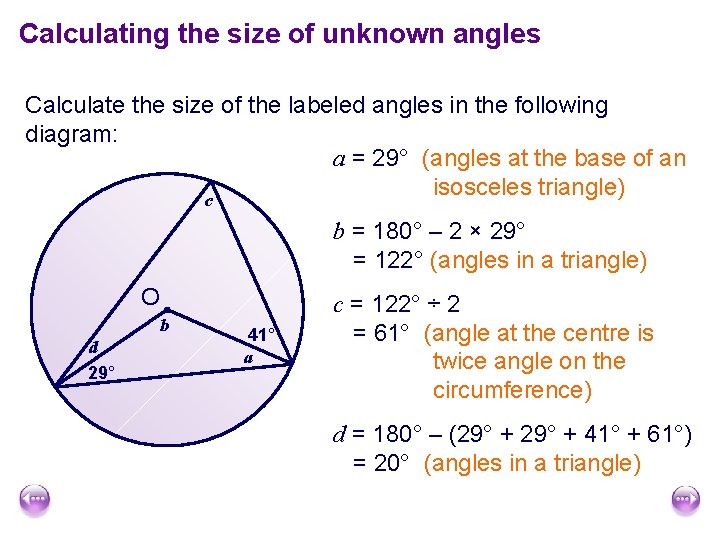
Calculating the size of unknown angles Calculate the size of the labeled angles in the following diagram: a = 29° (angles at the base of an isosceles triangle) c b = 180° – 2 × 29° = 122° (angles in a triangle) O b d 29° 41° a c = 122° ÷ 2 = 61° (angle at the centre is twice angle on the circumference) d = 180° – (29° + 41° + 61°) = 20° (angles in a triangle)

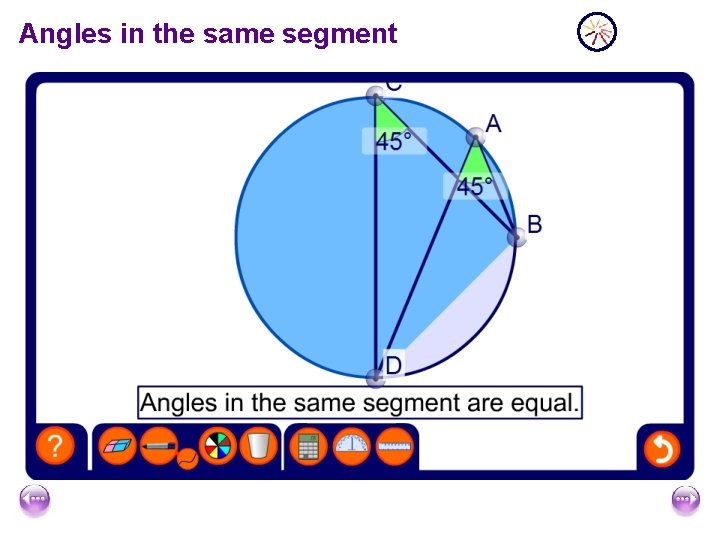
Angles in the same segment

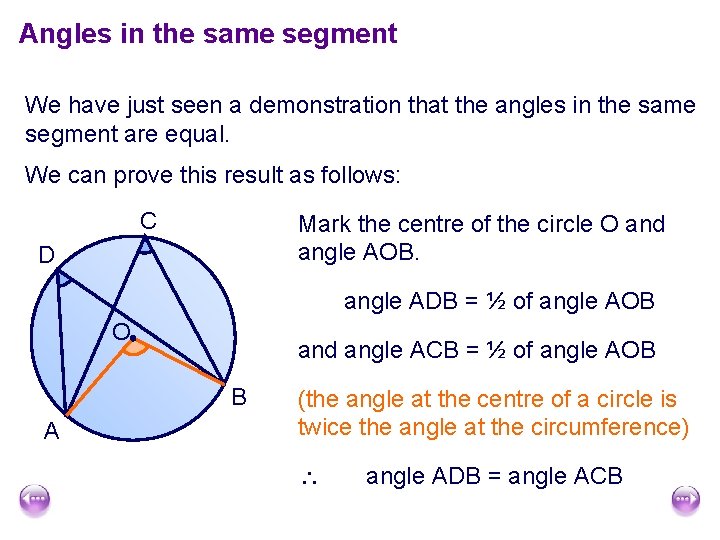
Angles in the same segment We have just seen a demonstration that the angles in the same segment are equal. We can prove this result as follows: C Mark the centre of the circle O and angle AOB. D angle ADB = ½ of angle AOB O and angle ACB = ½ of angle AOB B A (the angle at the centre of a circle is twice the angle at the circumference) angle ADB = angle ACB

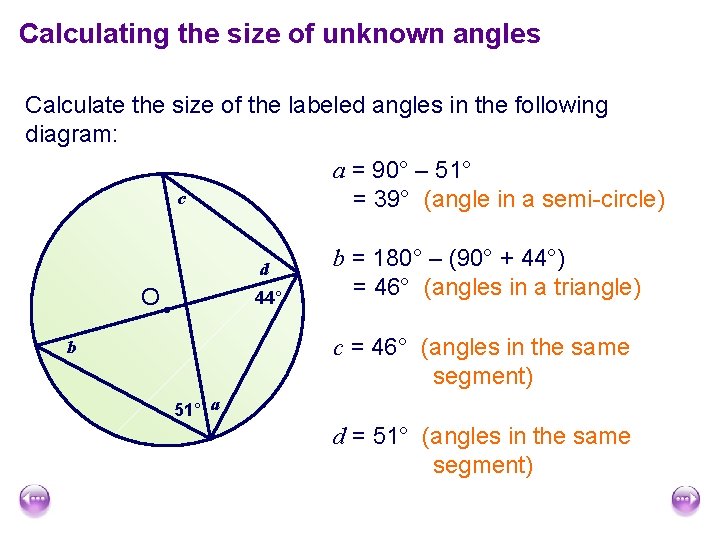
Calculating the size of unknown angles Calculate the size of the labeled angles in the following diagram: a = 90° – 51° c = 39° (angle in a semi-circle) d O 44° b = 180° – (90° + 44°) = 46° (angles in a triangle) c = 46° (angles in the same segment) b 51° a d = 51° (angles in the same segment)

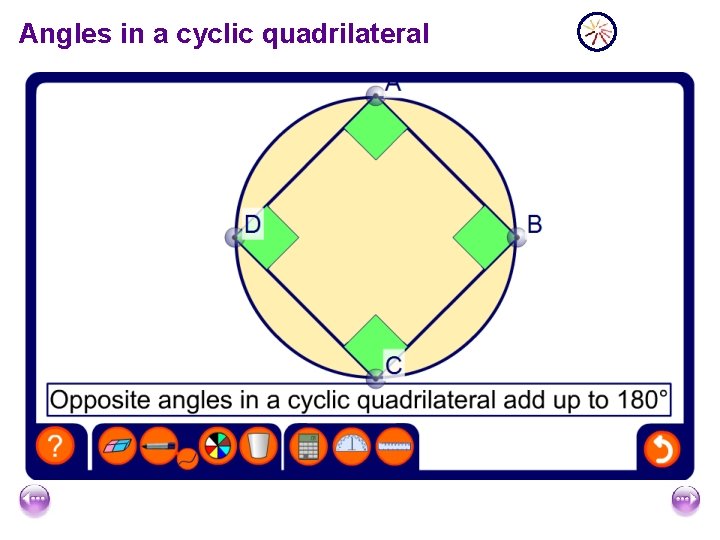
Angles in a cyclic quadrilateral

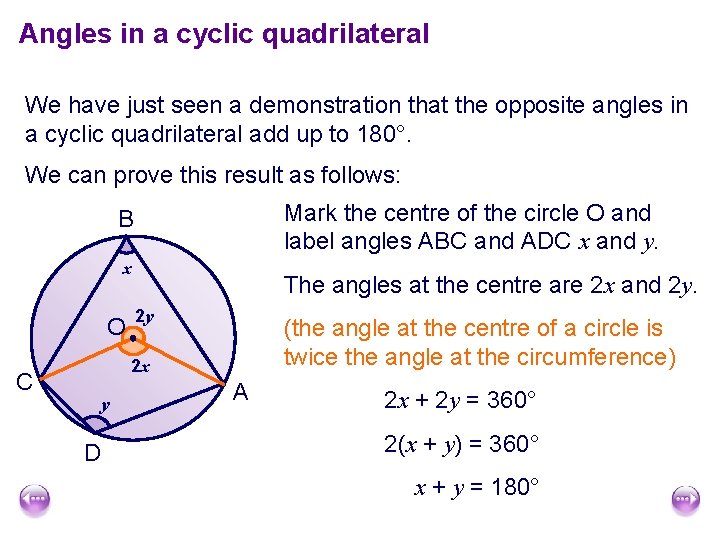
Angles in a cyclic quadrilateral We have just seen a demonstration that the opposite angles in a cyclic quadrilateral add up to 180°. We can prove this result as follows: Mark the centre of the circle O and label angles ABC and ADC x and y. B x O C The angles at the centre are 2 x and 2 y. 2 y (the angle at the centre of a circle is twice the angle at the circumference) 2 x y D A 2 x + 2 y = 360° 2(x + y) = 360° x + y = 180°

Angles in a cyclic quadrilateral As a result of this theorem we can conclude that is the opposite angle of a quadrilateral add up to 180° a circle can be drawn through each of its vertices. For example, the opposite angles in this quadrilateral add up to 180°. 67° It is a cyclic quadrilateral. 109° 113° 71° Remember that when two angles add up to 180° they are often called supplementary angles.

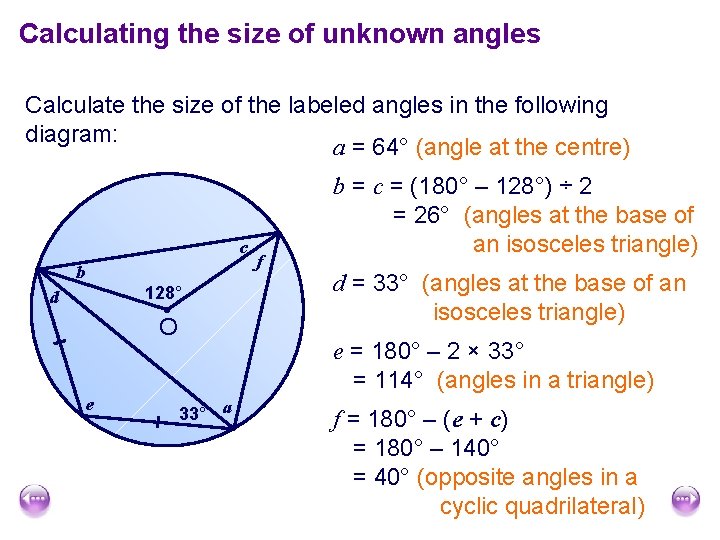
Calculating the size of unknown angles Calculate the size of the labeled angles in the following diagram: a = 64° (angle at the centre) c b 128° d O e f b = c = (180° – 128°) ÷ 2 = 26° (angles at the base of an isosceles triangle) d = 33° (angles at the base of an isosceles triangle) e = 180° – 2 × 33° = 114° (angles in a triangle) 33° a f = 180° – (e + c) = 180° – 140° = 40° (opposite angles in a cyclic quadrilateral)

Contents S 5 Circles A S 5. 1 Naming circle parts A S 5. 2 Angles in a circle A S 5. 3 Tangents and chords A S 5. 4 Circumference and arc length A S 5. 5 Areas of circles and sectors

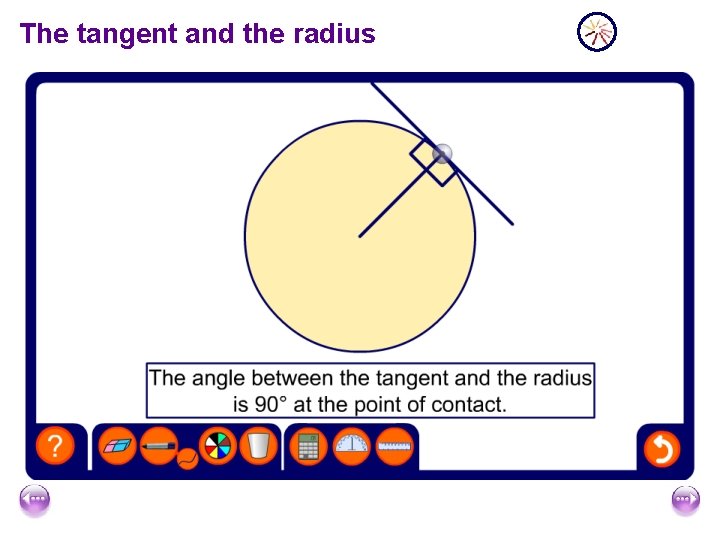
The tangent and the radius

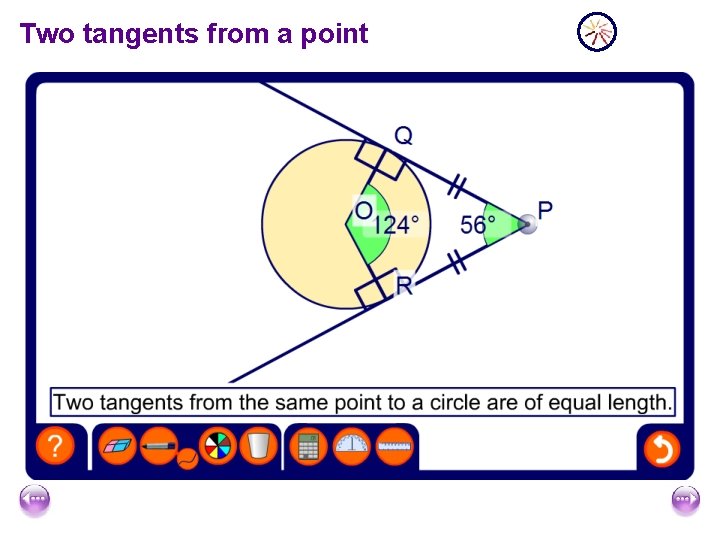
Two tangents from a point

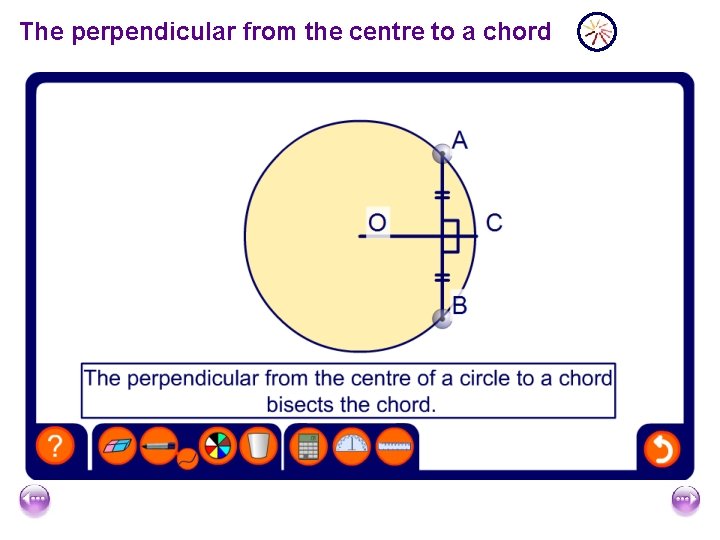
The perpendicular from the centre to a chord

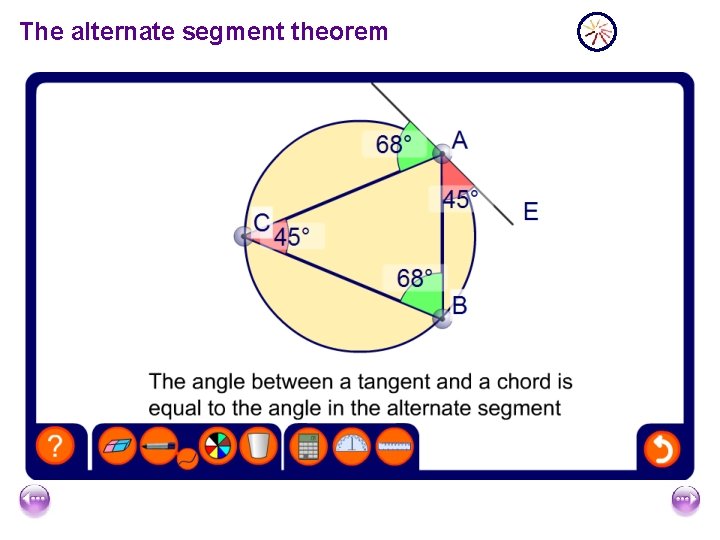
The alternate segment theorem

Contents S 5 Circles A S 5. 1 Naming circle parts A S 5. 2 Angles in a circle A S 5. 3 Tangents and chords A S 5. 4 Circumference and arc length A S 5. 5 Areas of circles and sectors

The value of π For any circle the circumference is always just over three times bigger than the radius. The exact number is called π (pi). We use the symbol π because the number cannot be written exactly. π = 3. 141592653589793238462643383279502884197169 39937510582097494459230781640628620899862803482 53421170679821480865132823066470938446095505822 31725359408128481117450284102701938521105559644 62294895493038196 (to 200 decimal places)!

Approximations for the value of π When we are doing calculations involving the value π we have to use an approximation for the value. For a rough approximation we can use 3. Better approximations are 3. 14 or 22. 7 We can also use the π button on a calculator. Most questions will tell you what approximations to use. When a calculation has lots of steps we write π as a symbol throughout and evaluate it at the end, if necessary.

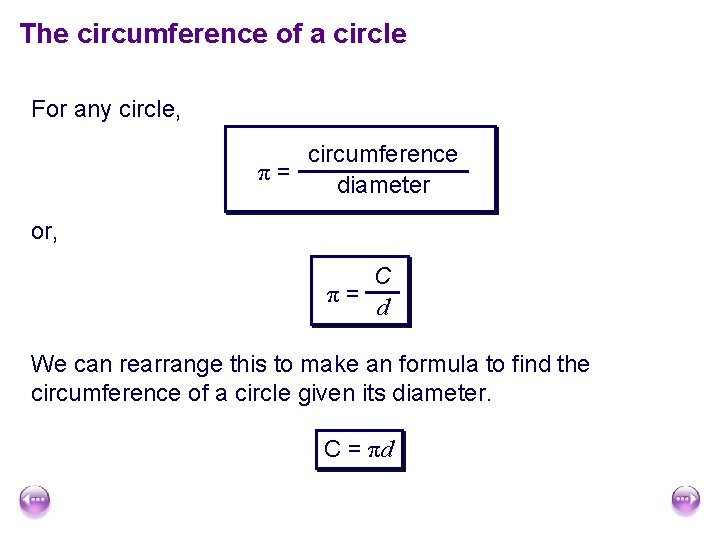
The circumference of a circle For any circle, circumference π= diameter or, C π= d We can rearrange this to make an formula to find the circumference of a circle given its diameter. C = πd

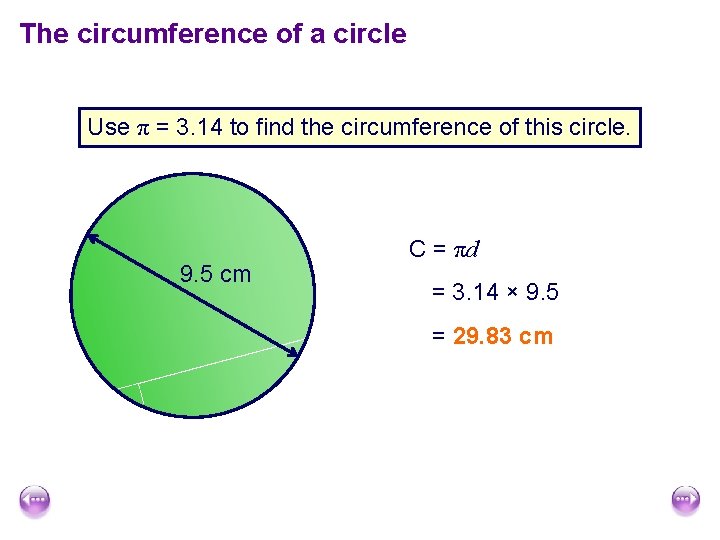
The circumference of a circle Use π = 3. 14 to find the circumference of this circle. 9. 5 cm C = πd = 3. 14 × 9. 5 = 29. 83 cm

Finding the circumference given the radius The diameter of a circle is two times its radius, or d = 2 r We can substitute this into the formula C = πd to give us a formula to find the circumference of a circle given its radius. C = 2πr

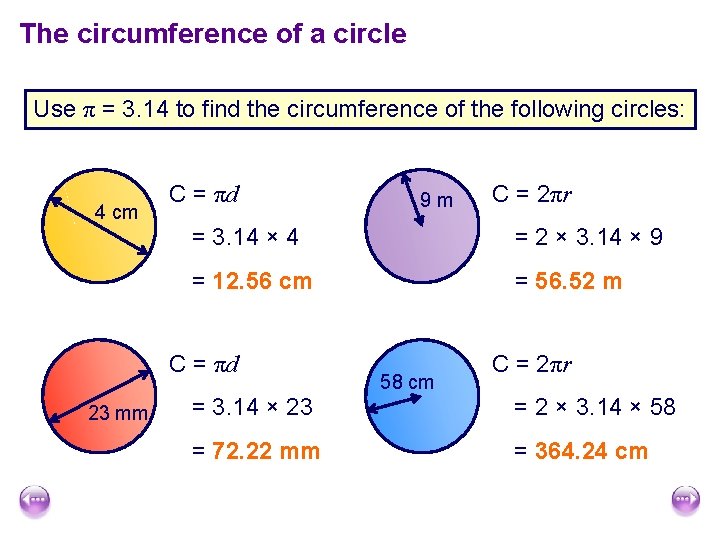
The circumference of a circle Use π = 3. 14 to find the circumference of the following circles: 4 cm C = πd C = 2πr = 3. 14 × 4 = 2 × 3. 14 × 9 = 12. 56 cm = 56. 52 m C = πd 23 mm 9 m 58 cm C = 2πr = 3. 14 × 23 = 2 × 3. 14 × 58 = 72. 22 mm = 364. 24 cm

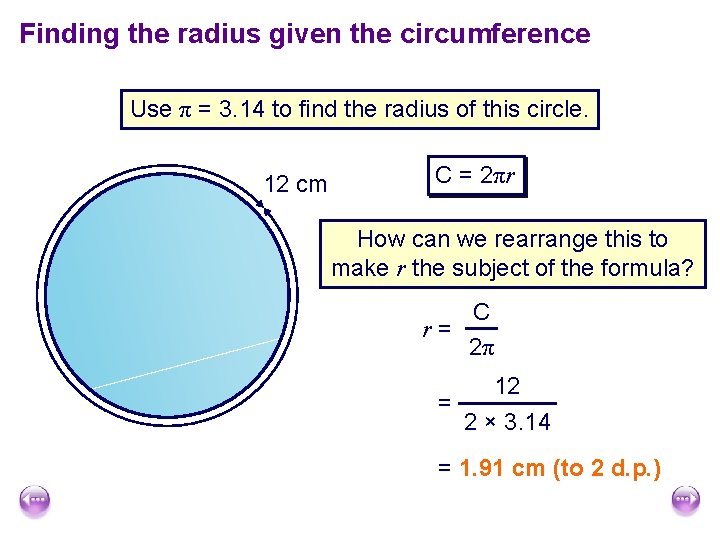
Finding the radius given the circumference Use π = 3. 14 to find the radius of this circle. 12 cm C = 2πr How can we rearrange this to make r the subject of the formula? C r= ? 2π 12 = 2 × 3. 14 = 1. 91 cm (to 2 d. p. )

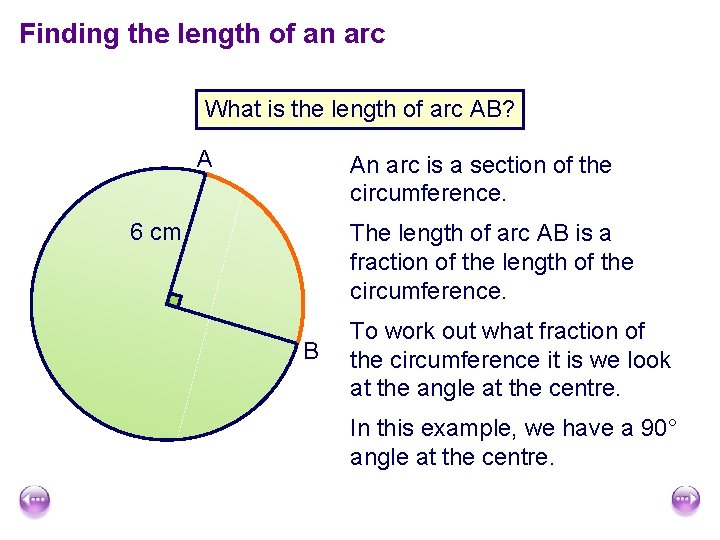
Finding the length of an arc What is the length of arc AB? A An arc is a section of the circumference. 6 cm The length of arc AB is a fraction of the length of the circumference. B To work out what fraction of the circumference it is we look at the angle at the centre. In this example, we have a 90° angle at the centre.

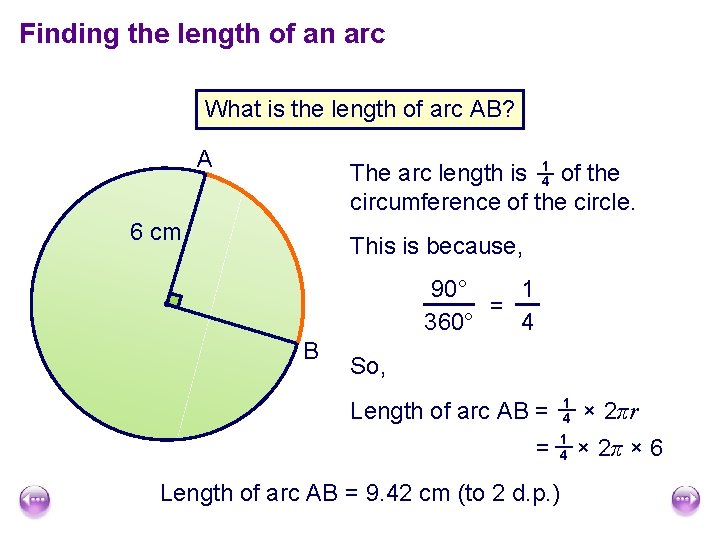
Finding the length of an arc What is the length of arc AB? A The arc length is 14 of the circumference of the circle. 6 cm This is because, 90° 1 = 4 360° B So, Length of arc AB = 1 4 Length of arc AB = 9. 42 cm (to 2 d. p. ) × 2πr × 2π × 6

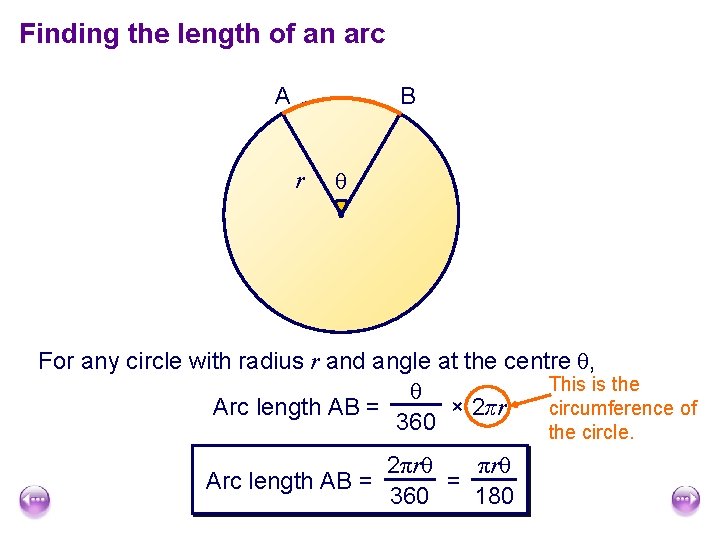
Finding the length of an arc A B r θ For any circle with radius r and angle at the centre θ, This is the θ × 2πr Arc length AB = circumference of 360 the circle. 2πrθ Arc length AB = = 360 180

Finding the length of an arc

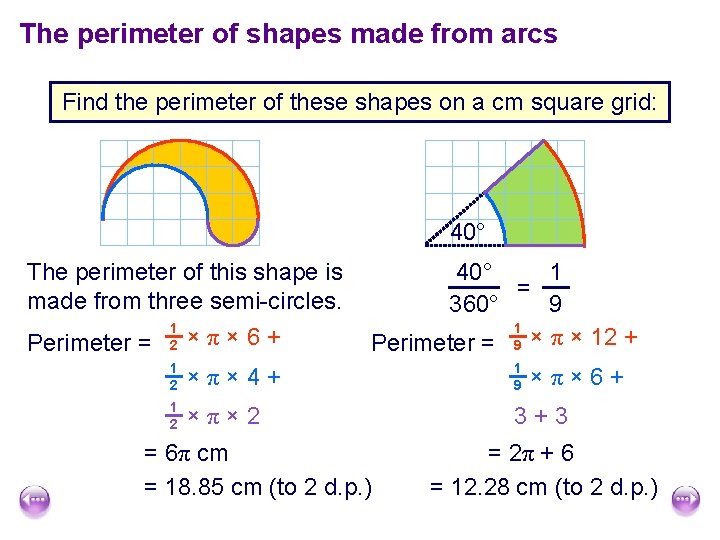
The perimeter of shapes made from arcs Find the perimeter of these shapes on a cm square grid: 40° The perimeter of this shape is made from three semi-circles. Perimeter = 40° 1 = 360° 9 1 Perimeter = 9 × π × 12 + 1 2 ×π× 6+ 1 2 ×π× 4+ 1 9 1 2 ×π× 2 3+3 = 6π cm = 18. 85 cm (to 2 d. p. ) ×π× 6+ = 2π + 6 = 12. 28 cm (to 2 d. p. )

Contents S 5 Circles A S 5. 1 Naming circle parts A S 5. 2 Angles in a circle A S 5. 3 Tangents and chords A S 5. 4 Circumference and arc length A S 5. 5 Areas of circles and sectors

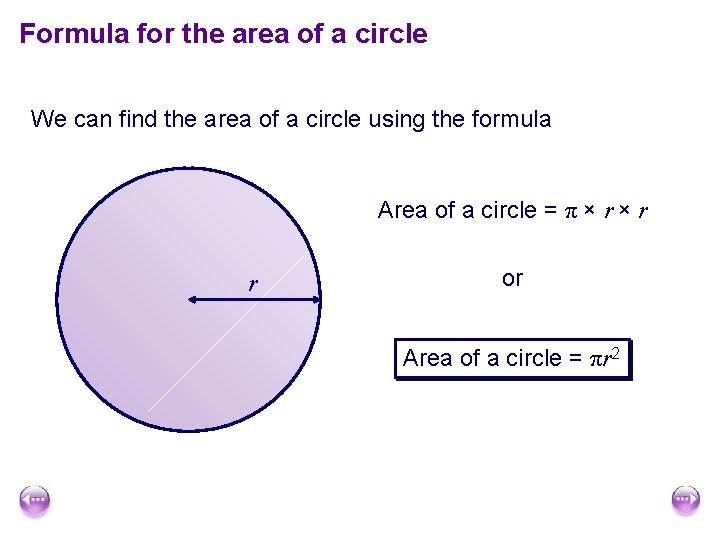
Formula for the area of a circle We can find the area of a circle using the formula Area of a circle = π × r r or Area of a circle = πr 2

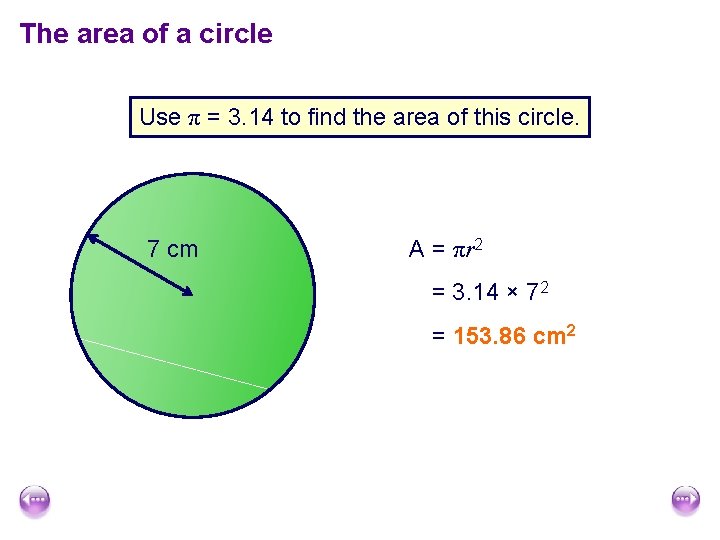
The area of a circle Use π = 3. 14 to find the area of this circle. 7 cm A = πr 2 = 3. 14 × 72 = 153. 86 cm 2

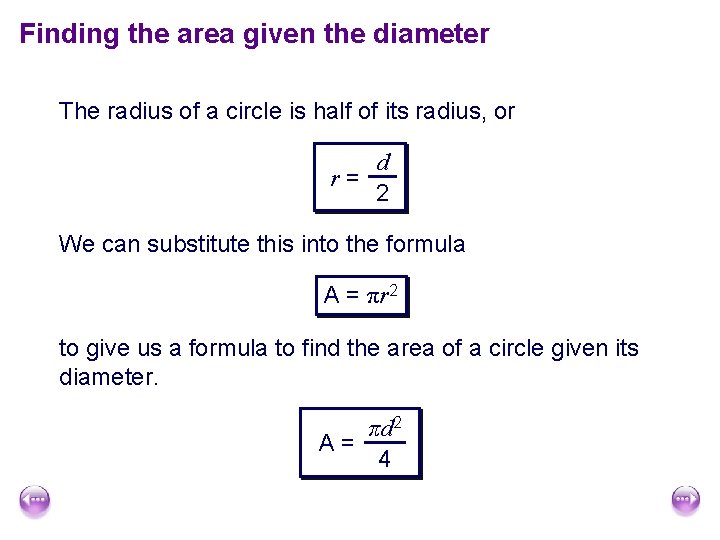
Finding the area given the diameter The radius of a circle is half of its radius, or d r= 2 We can substitute this into the formula A = πr 2 to give us a formula to find the area of a circle given its diameter. πd 2 A= 4

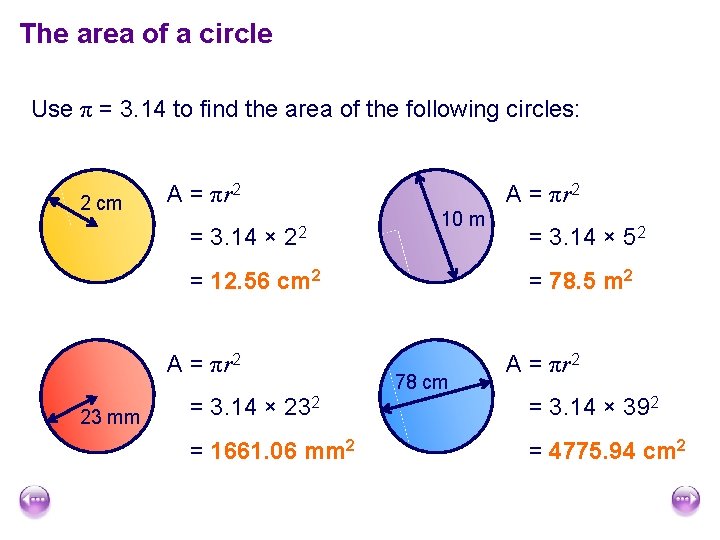
The area of a circle Use π = 3. 14 to find the area of the following circles: 2 cm A = πr 2 = 3. 14 × A = πr 2 22 10 m = 12. 56 cm 2 A = πr 2 23 mm = 3. 14 × 52 = 78. 5 m 2 78 cm A = πr 2 = 3. 14 × 232 = 3. 14 × 392 = 1661. 06 mm 2 = 4775. 94 cm 2

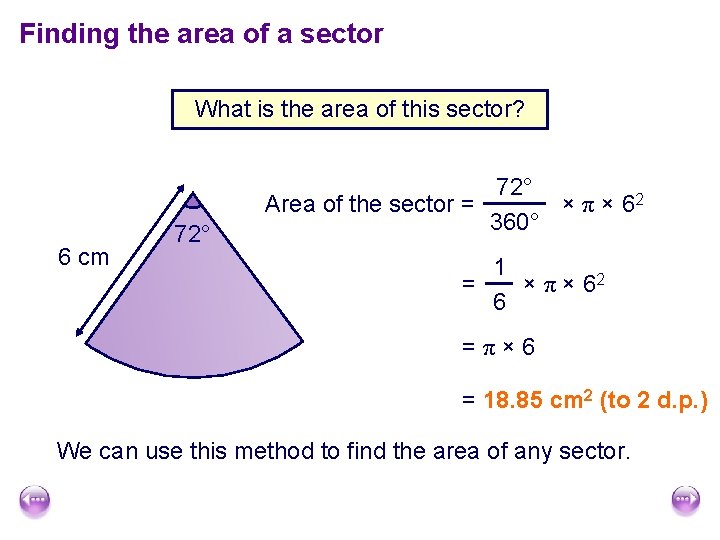
Finding the area of a sector What is the area of this sector? 6 cm 72° × π × 62 Area of the sector = 360° 1 = × π × 62 6 =π× 6 = 18. 85 cm 2 (to 2 d. p. ) We can use this method to find the area of any sector.

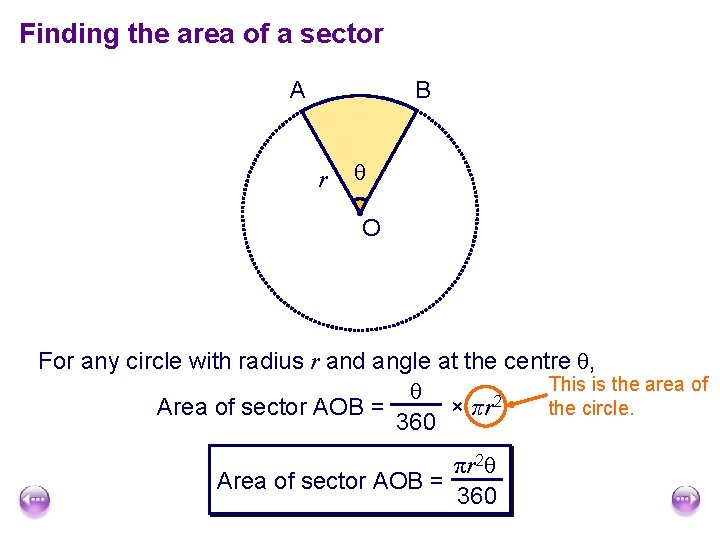
Finding the area of a sector A B r θ O For any circle with radius r and angle at the centre θ, This is the area of θ × πr 2 Area of sector AOB = the circle. 360 πr 2θ Area of sector AOB = 360

Finding the area of a sector

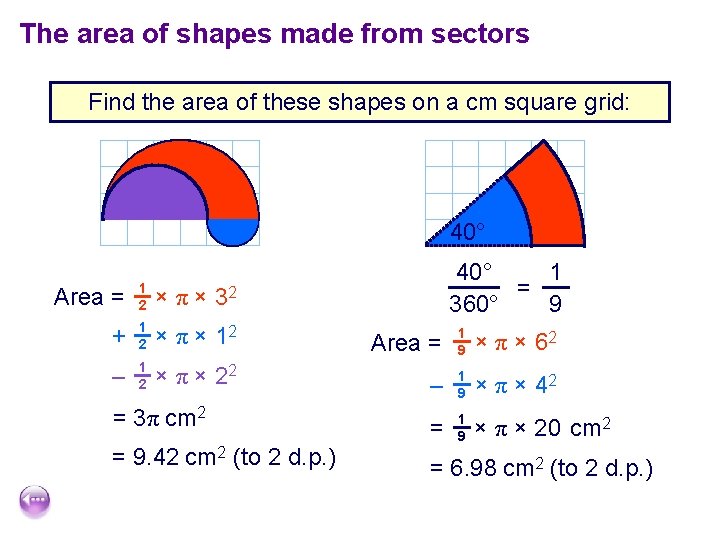
The area of shapes made from sectors Find the area of these shapes on a cm square grid: 40° 1 = 360° 9 Area = 1 2 × π × 32 + 1 2 × π × 12 Area = 1 9 × π × 62 – 1 2 × π × 22 – 1 9 × π × 42 = 3π cm 2 = × π × 20 cm 2 = 9. 42 cm 2 (to 2 d. p. ) 1 9 = 6. 98 cm 2 (to 2 d. p. )