Circle Theorem Proofs SemiCircle Centre Cyclic Quadrilateral Same

HOME Angle at the centre x° 2 x° Angle at the centre is double

HOME PROOF: - First, draw a radius => 2 Isosceles Triangles = (180 –

HOME Angle in a Semi-Circle Angle in a semi-circle is 90°

PROOF: - First, draw a radius HOME => 2 Isosceles Triangles - Label an

HOME Opposite Angles in a Cyclic Quadrilateral x 2 y 2 x y Opposite

HOME PROOF: x First, draw in radii apply ‘angle at centre’ 2 y 2

HOME Angles in Same Segment Angles created by triangles are equal if they are

HOME PROOF: - First, draw in radii apply ‘angle at centre’ again x 2

HOME PROOF: - First, draw in radii x x apply ‘angle at centre’ 2

HOME Ch o d Chor rd Alternate Segment Theorem Angle between a tangent and

PROOF: Start with two of the circle theorems HOME Angle between a tangent and

HOME PROOF: Label an angle For cases when chord isn’t a diameter? x 90

HOME Lengths of Tangents A C B Tangents to a circle which meet at

PROOF: - Connect meeting point to centre HOME - Draw radii in apply ‘angle

HOME http: //app. myimaths. com/2101 -resource/circle-theorem-proof Radius to a Tangent is 90 o O

Slides: 17

Download presentation

Circle Theorem Proofs Semi-Circle Centre Cyclic Quadrilateral Same Segment Alternate Segment Tangents

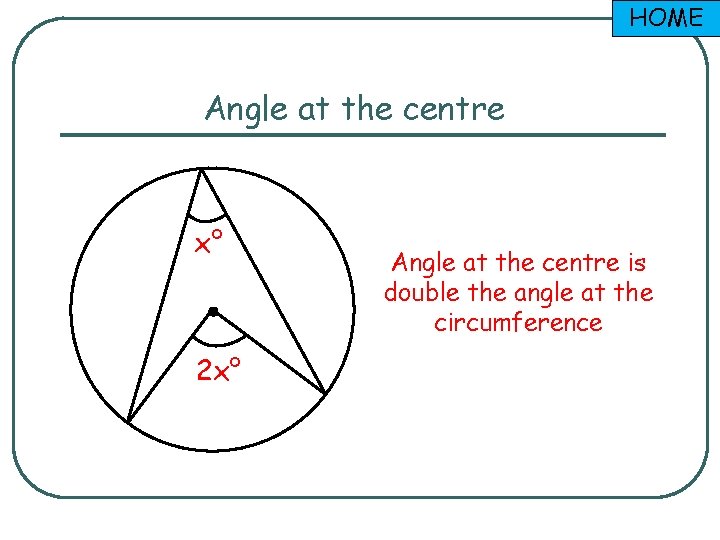
HOME Angle at the centre x° 2 x° Angle at the centre is double the angle at the circumference

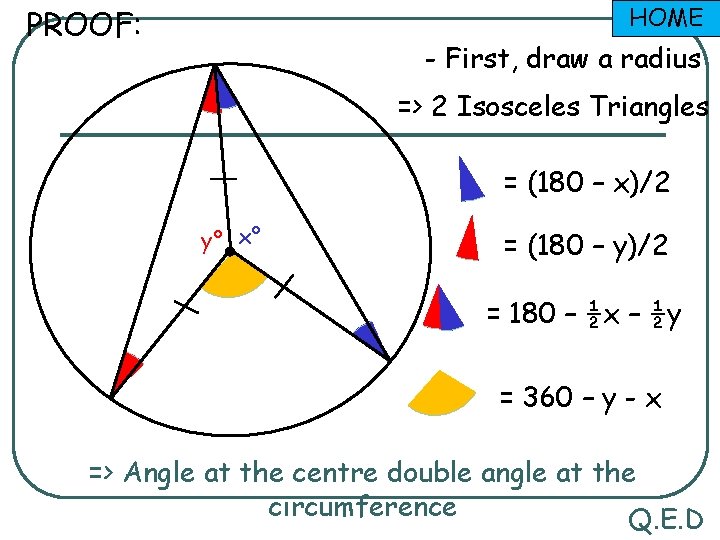
HOME PROOF: - First, draw a radius => 2 Isosceles Triangles = (180 – x)/2 y° x° = (180 – y)/2 = 180 – ½x – ½y = 360 – y - x => Angle at the centre double angle at the circumference Q. E. D

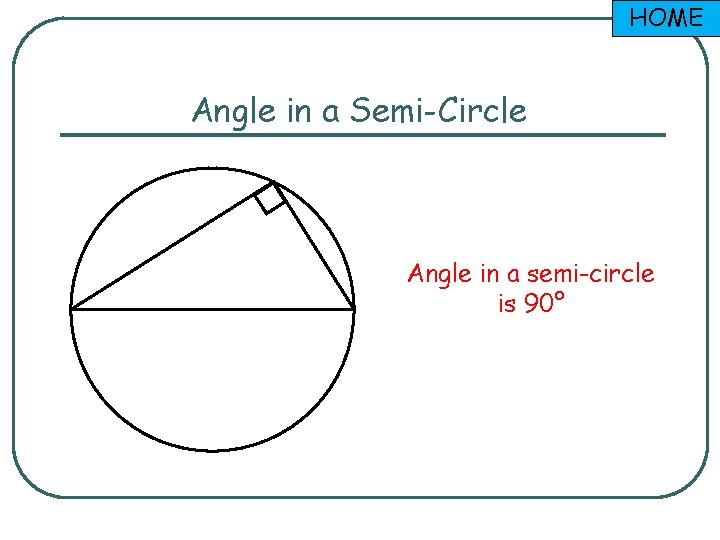
HOME Angle in a Semi-Circle Angle in a semi-circle is 90°

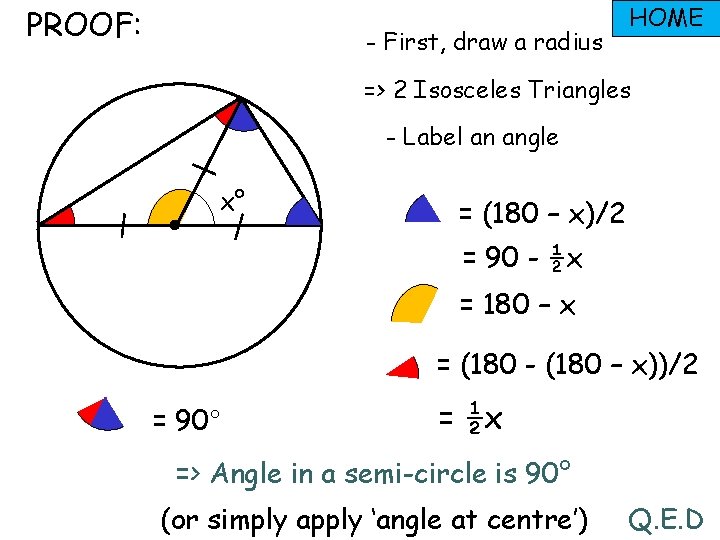
PROOF: - First, draw a radius HOME => 2 Isosceles Triangles - Label an angle x° = (180 – x)/2 = 90 - ½x = 180 – x = (180 - (180 – x))/2 = 90° = ½x => Angle in a semi-circle is 90° (or simply apply ‘angle at centre’) Q. E. D

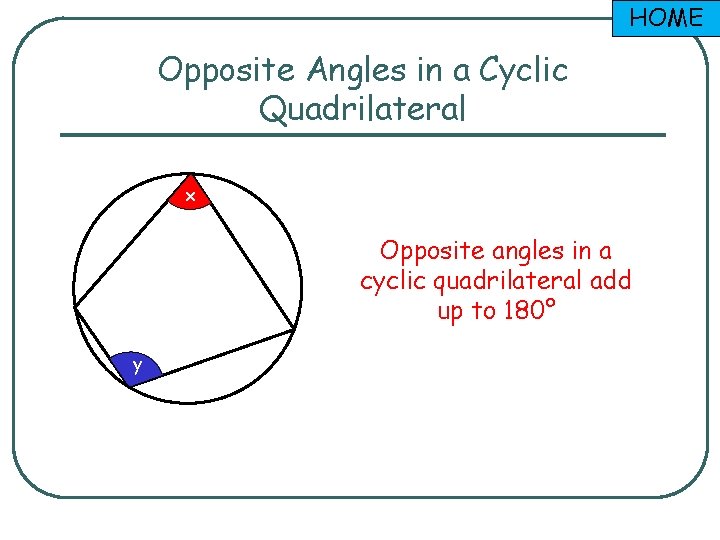
HOME Opposite Angles in a Cyclic Quadrilateral x 2 y 2 x y Opposite angles in a cyclic quadrilateral add up to 180°

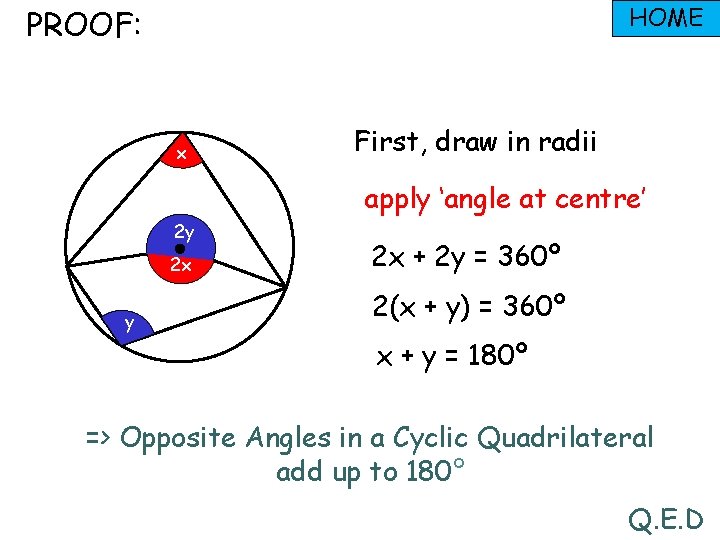
HOME PROOF: x First, draw in radii apply ‘angle at centre’ 2 y 2 x + 2 y = 360º 2(x + y) = 360º x + y = 180º => Opposite Angles in a Cyclic Quadrilateral add up to 180° Q. E. D

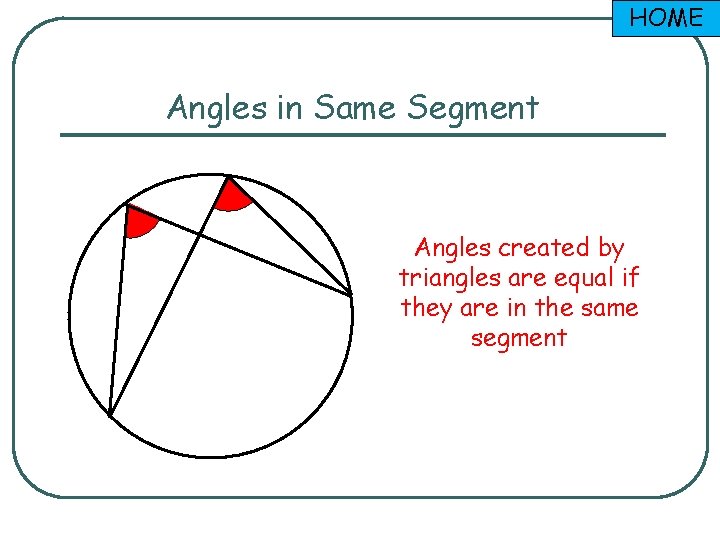
HOME Angles in Same Segment Angles created by triangles are equal if they are in the same segment

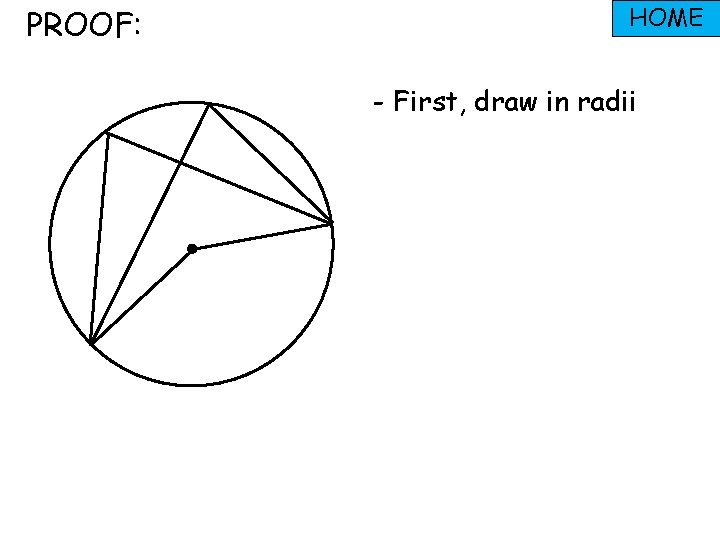
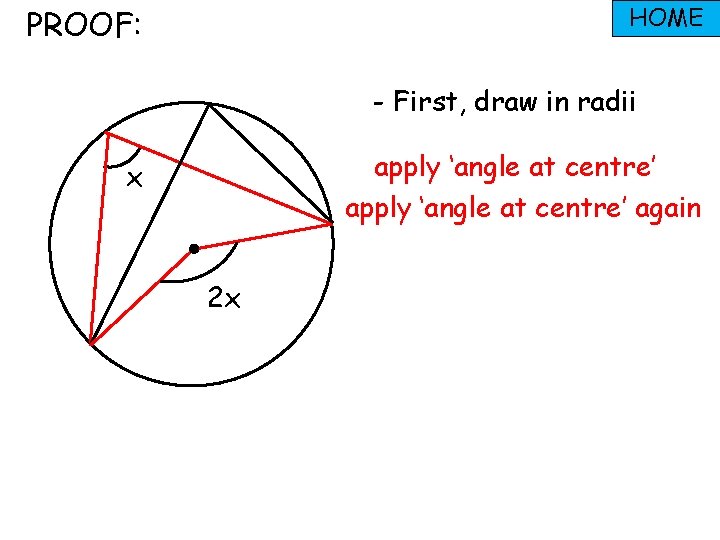
PROOF: HOME - First, draw in radii

HOME PROOF: - First, draw in radii apply ‘angle at centre’ again x 2 x

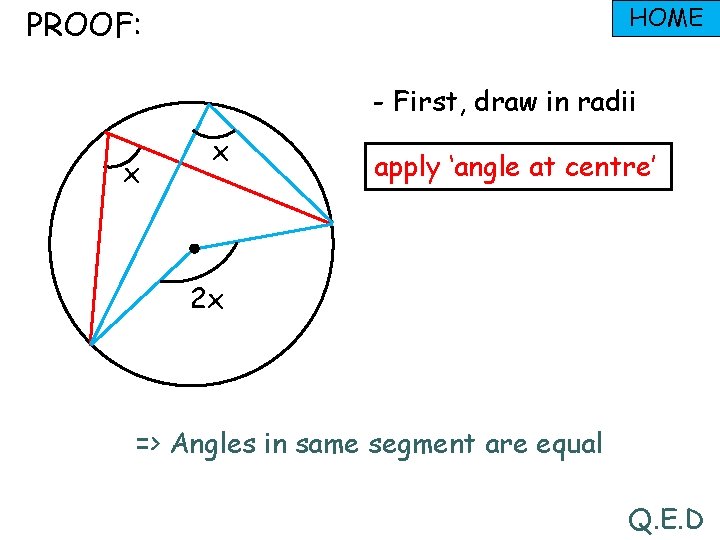
HOME PROOF: - First, draw in radii x x apply ‘angle at centre’ 2 x => Angles in same segment are equal Q. E. D

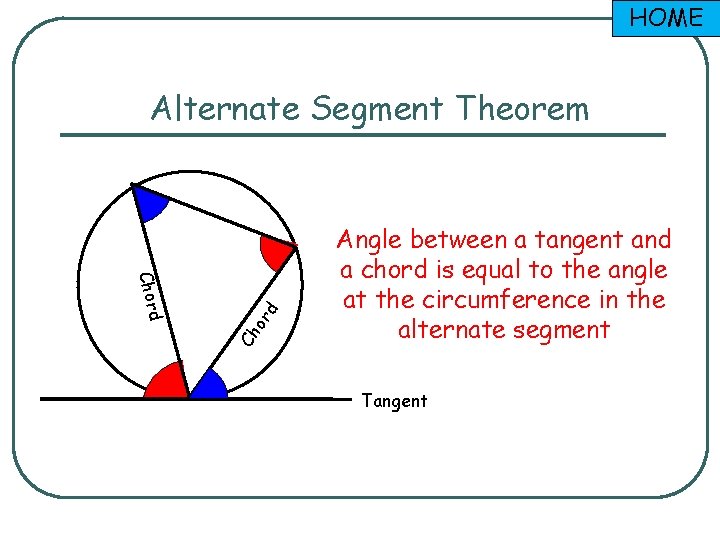
HOME Ch o d Chor rd Alternate Segment Theorem Angle between a tangent and a chord is equal to the angle at the circumference in the alternate segment Tangent

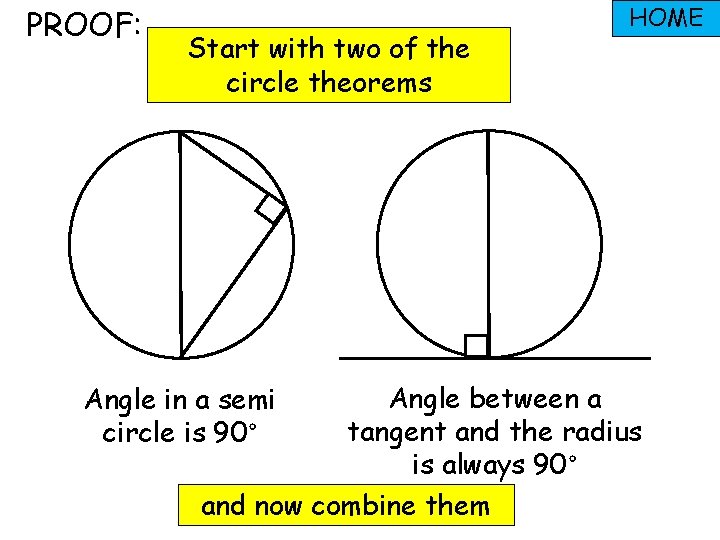
PROOF: Start with two of the circle theorems HOME Angle between a tangent and the radius is always 90° and now combine them Angle in a semi circle is 90°

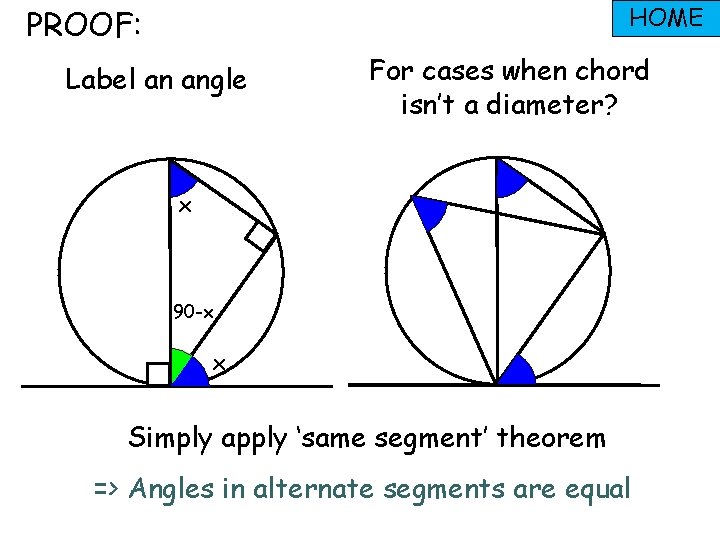
HOME PROOF: Label an angle For cases when chord isn’t a diameter? x 90 -x x Simply apply ‘same segment’ theorem => Angles in alternate segments are equal

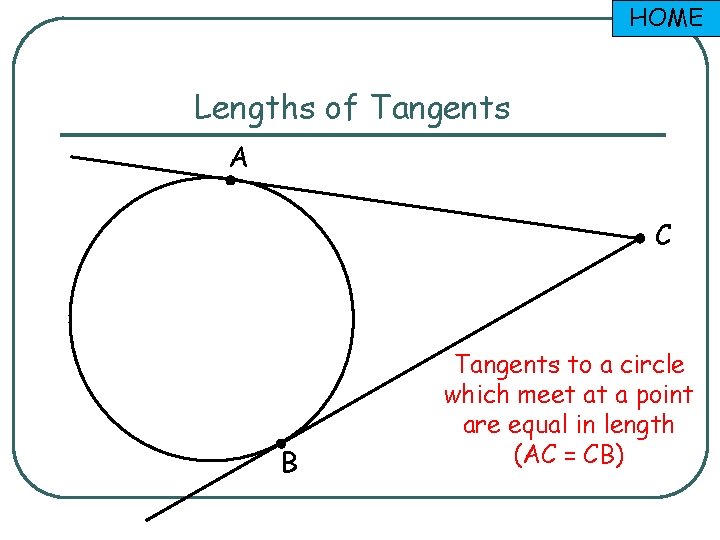
HOME Lengths of Tangents A C B Tangents to a circle which meet at a point are equal in length (AC = CB)

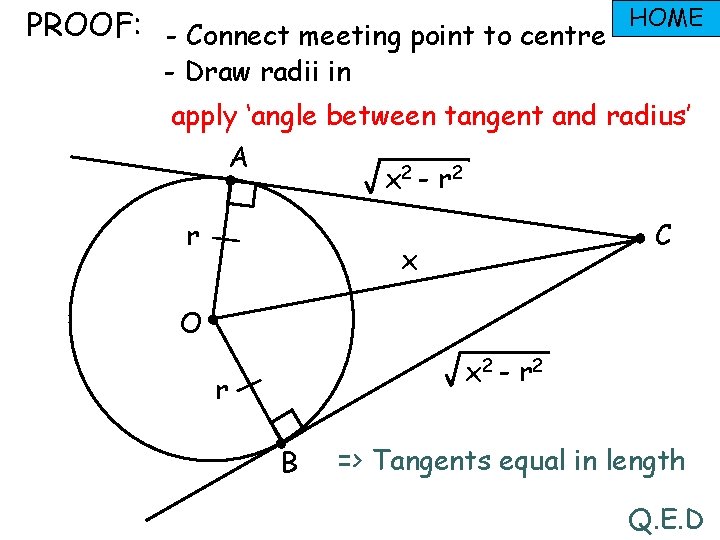
PROOF: - Connect meeting point to centre HOME - Draw radii in apply ‘angle between tangent and radius’ A x 2 - r 2 r C x O x 2 - r 2 r B => Tangents equal in length Q. E. D

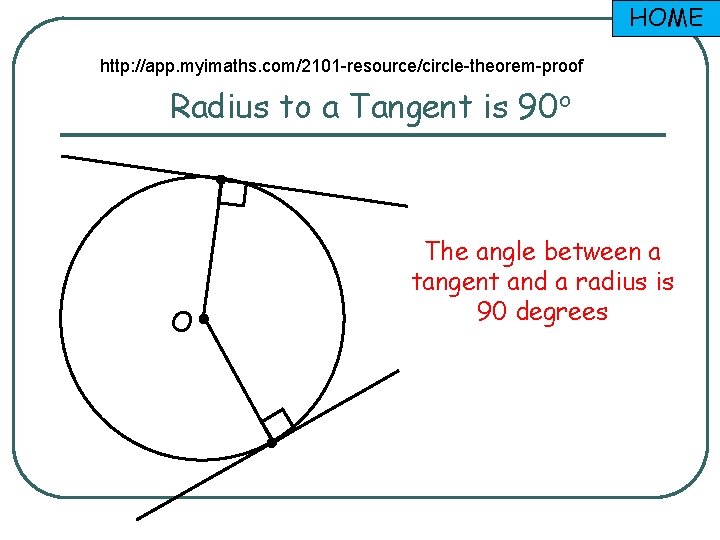
HOME http: //app. myimaths. com/2101 -resource/circle-theorem-proof Radius to a Tangent is 90 o O The angle between a tangent and a radius is 90 degrees