Circle Generating Algorithms w Circles and ellipses are

Circle Generating Algorithms w Circles and ellipses are common components in many pictures. w Circle generation routines are often included in packages. 1

Circle Equations w Polar form x = r. Cos y = r. Sin (r = radius of circle) y P=(r. Cos , r. Sin ) r r. Cos ) r. Sin ) x 2

Drawing a circle = 0° while ( < 360°) x = r. Cos y = r. Sin set. Pixel(x, y) = + 1° end while Disadvantages w To find a complete circle varies from 0° to 360° w The calculation of trigonometric functions is very slow. 3

Cartesian form w Use Pythagoras theorem x 2 + y 2 = r 2 r y x y r y x x 4

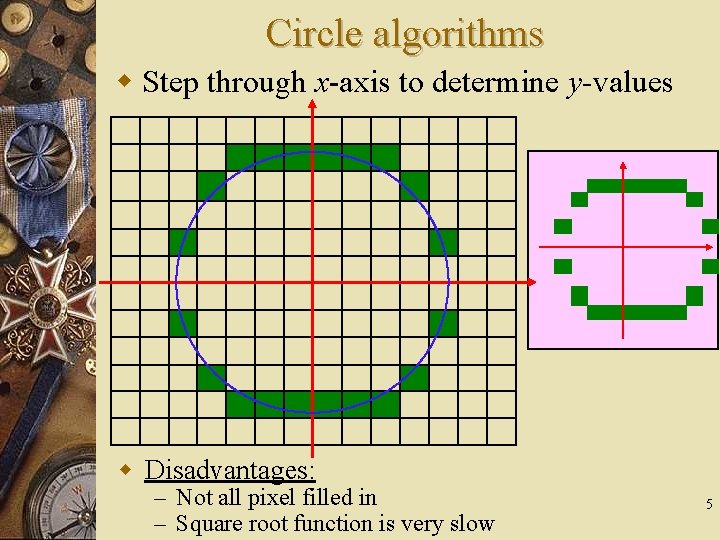
Circle algorithms w Step through x-axis to determine y-values w Disadvantages: – Not all pixel filled in – Square root function is very slow 5

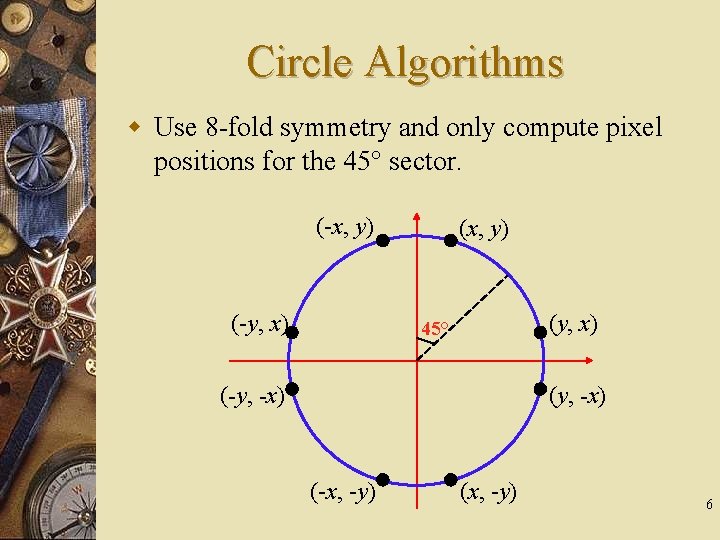
Circle Algorithms w Use 8 -fold symmetry and only compute pixel positions for the 45° sector. (-x, y) (-y, x) (x, y) (y, x) 45° (-y, -x) (-x, -y) (x, -y) 6

Bresenham’s Circle Algorithm Consider only 45° ≤ ≤ 90° General Principle w The circle function: w and 7

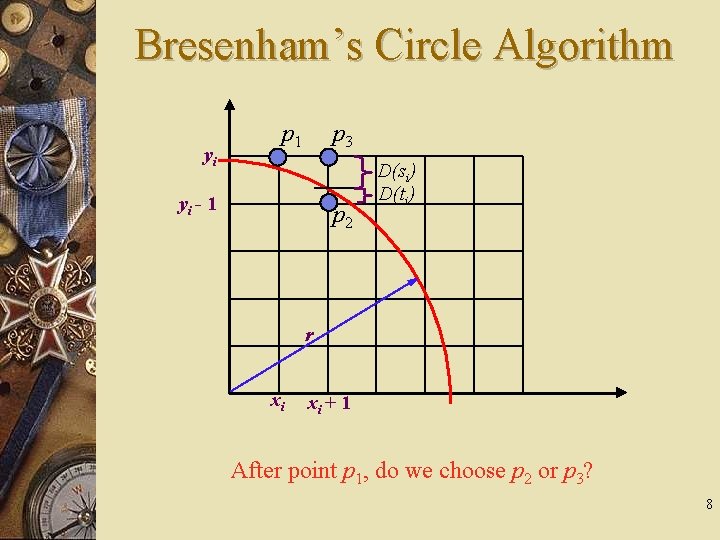
Bresenham’s Circle Algorithm yi p 1 p 3 yi - 1 p 2 D(si) D(ti) r xi xi + 1 After point p 1, do we choose p 2 or p 3? 8

Bresenham’s Circle Algorithm Define: D(si) = distance of p 3 from circle D(ti) = distance of p 2 from circle i. e. D(si) = (xi + 1)2 + yi 2 – r 2 [always +ve] D(ti) = (xi + 1)2 + (yi – 1)2 – r 2 [always -ve] w Decision Parameter pi = D(si) + D(ti) so if pi < 0 then the circle is closer to p 3 (point above) if pi ≥ 0 then the circle is closer to p 2 (point below) 9

The Algorithm x 0 = 0 y 0 = r p 0 = [12 + r 2 – r 2] + [12 + (r-1)2 – r 2] = 3 – 2 r if pi < 0 then yi+1 = yi pi+1 = pi + 4 xi + 6 else if pi ≥ 0 then yi+1 = yi – 1 pi+1 = pi + 4(xi – yi) + 10 xi+1 = xi + 1 w Stop when xi ≥ yi and determine symmetry points in the other octants 10

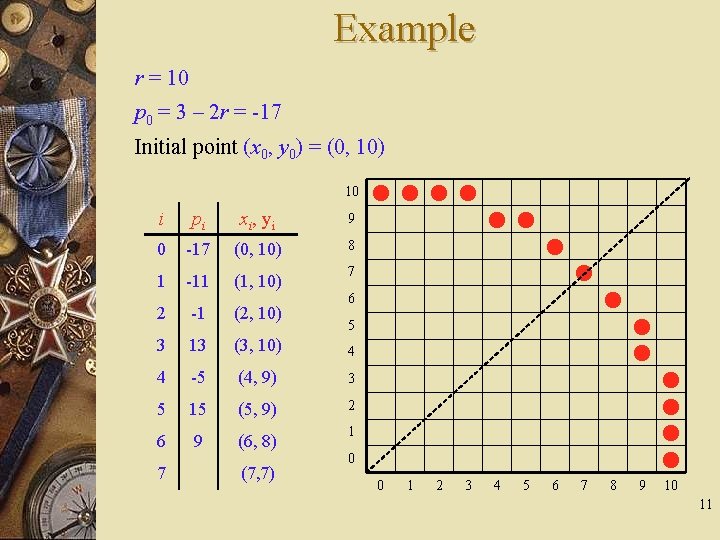
Example r = 10 p 0 = 3 – 2 r = -17 Initial point (x 0, y 0) = (0, 10) 10 i pi xi, yi 9 0 -17 (0, 10) 8 1 -11 (1, 10) 2 -1 (2, 10) 3 13 4 7 6 5 (3, 10) 4 -5 (4, 9) 3 5 15 (5, 9) 2 6 9 (6, 8) 1 0 7 (7, 7) 0 1 2 3 4 5 6 7 8 9 10 11

Exercises w Draw the circle with r = 12 using the Bresenham algorithm. w Draw the circle with r = 14 and center at (15, 10). 12

Decision Parameters w Prove that if pi < 0 and yi+1 = yi then pi+1 = pi + 4 xi + 6 w Prove that if pi ≥ 0 and yi+1 = yi – 1 then pi+1 = pi + 4(xi – yi) + 10 13

Advantages of Bresenham circle w Only involves integer addition, subtraction and multiplication w There is no need for squares, square roots and trigonometric functions 14

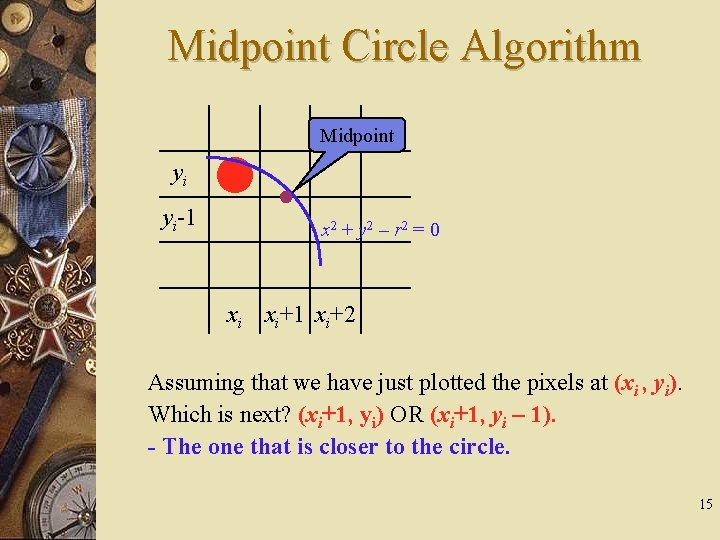
Midpoint Circle Algorithm Midpoint yi yi-1 x 2 + y 2 – r 2 = 0 xi xi+1 xi+2 Assuming that we have just plotted the pixels at (xi , yi). Which is next? (xi+1, yi) OR (xi+1, yi – 1). - The one that is closer to the circle. 15

Midpoint Circle Algorithm w The decision parameter is the circle at the midpoint between the pixels yi and yi – 1. w If pi < 0, the midpoint is inside the circle and the pixel yi is closer to the circle boundary. w If pi ≥ 0, the midpoint is outside the circle and the pixel yi - 1 is closer to the circle boundary. 16

Decision Parameters w Decision Parameters are obtained using incremental calculations Note: xi+1 = xi +1 OR where yi+1 is either yi or yi-1 depending on the sign of pi 17

1. 2. 3. 4. 5. 6. Initial values: - point(0, r) x 0 = 0 y 0 = r Initial decision parameter The Algorithm move circle origin at (0, 0) by x = x – xc and y = y – yc At each xi position, starting at i = 0, perform the following test: if pi < 0, the next point is (xi + 1, yi) and pi+1 = pi + 2 xi+1 + 1 If pi ≥ 0, the next point is (xi+1, yi-1) and pi+1 = pi + 2 xi+1 + 1 – 2 yi+1 where 2 xi+1 = 2 xi + 2 and 2 yi+1 = 2 yi – 2 Determine symmetry points in the other octants Move pixel positions (x, y) onto the circular path centered on (xc, yc) and plot the coordinates: x = x + xc, y = y + yc 18 Repeat 3 – 5 until x ≥ y

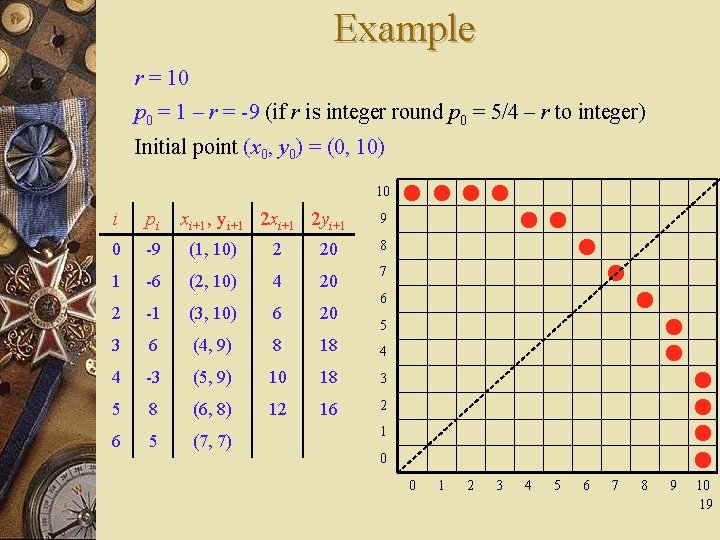
Example r = 10 p 0 = 1 – r = -9 (if r is integer round p 0 = 5/4 – r to integer) Initial point (x 0, y 0) = (0, 10) 10 i pi xi+1, yi+1 2 xi+1 2 yi+1 0 -9 (1, 10) 2 20 1 -6 (2, 10) 4 20 2 -1 (3, 10) 6 20 3 6 (4, 9) 8 4 -3 (5, 9) 5 8 (6, 8) 6 5 (7, 7) 9 8 7 6 5 18 4 10 18 3 12 16 2 1 0 0 1 2 3 4 5 6 7 8 9 10 19

Exercises w Draw the circle with r = 12 using the Midpoint-circle algorithm w Draw the circle with r = 14 and center at (15, 10). 20