CINEMTICA Movimiento Rectilneo Uniformemente Acelerado MRUA 1 Qu

CINEMÁTICA Movimiento Rectilíneo Uniformemente Acelerado (MRUA)

1. Qué es el movimiento. Movimiento y reposo Un cuerpo está en movimiento si cambia de posición con respecto al sistema de referencia; en caso contrario, está en reposo. Sistema de referencia es un punto respecto al cual se describe el movimiento de un cuerpo.

Movimiento y reposo Móvil es todo cuerpo capaz de desplazarse

Movimiento y reposo Actividades: 1. Si observas la fotografía de un tren, ¿puedes determinar si dicho tren está en reposo o en movimiento? ¿por qué? 2. Razona cómo es posible que un pasajero sentado en una butaca de un tren esté en reposo respecto al tren y al mismo tiempo en movimiento respecto a la estación.

Trayectoria y desplazamiento Trayectoria: línea formada por los sucesivos puntos que ocupa un móvil durante su desplazamiento. Desplazamiento entre dos puntos de la trayectoria es el vector que une ambos puntos. Vector: segmento orientado que indica la dirección, el sentido y el valor del desplazamiento

Trayectoria y desplazamiento La forma geométrica que describe la trayectoria de un móvil permite identificar distintos tipos de movimientos: - Rectilíneo: como un ascensor - Circular: giro de un CD, rueda de automóvil. - Elíptico: traslación de la Tierra - Parabólico: pelota de tenis en partido

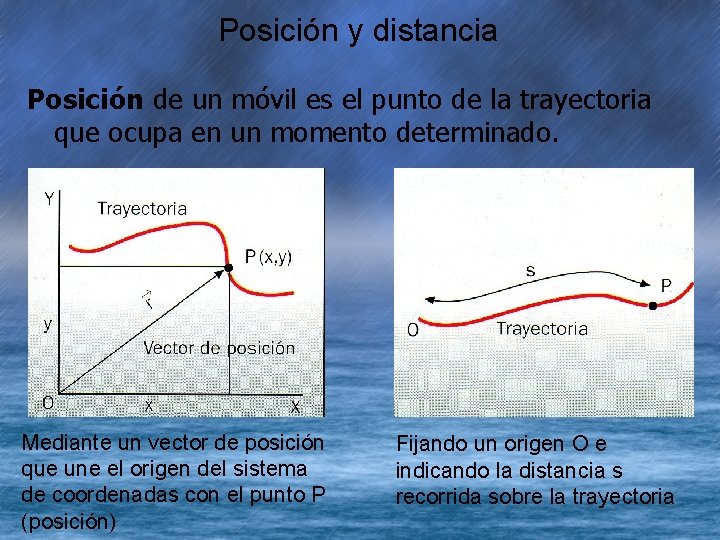
Posición y distancia Posición de un móvil es el punto de la trayectoria que ocupa en un momento determinado. Mediante un vector de posición que une el origen del sistema de coordenadas con el punto P (posición) Fijando un origen O e indicando la distancia s recorrida sobre la trayectoria

Posición y distancia Distancia recorrida en un intervalo de tiempo es la longitud, medida sobre la trayectoria, que existe entre las posiciones inicial y final del móvil en dicho intervalo de tiempo. Se calcula restando las posiciones final e inicial, medidas sobre la trayectoria: ΔS = s - s 0

Posición y distancia 7. Desplazamiento: diferencia entre posición final e inicial en línea recta. Distancia: diferencia entre posición final e inicial medida sobre la trayectoria 8. Entre 0 y 20 min: 500 m Entre 20 y 40 min: 900 m No, en el segundo caso ha ido más rápido pues ha recorrido más distancia en menos tiempo.

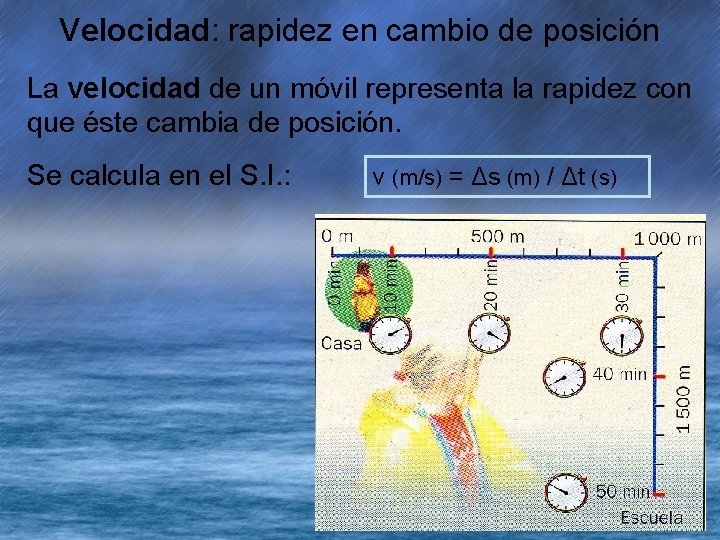
Velocidad: rapidez en cambio de posición La velocidad de un móvil representa la rapidez con que éste cambia de posición. Se calcula en el S. I. : v (m/s) = Δs (m) / Δt (s)

Velocidad Media e Instantánea La velocidad media es el cociente entre la distancia recorrida por el móvil y el tiempo empleado en recorrerla. La velocidad instantánea es la que tiene un móvil en un instante determinado.

Cambios en la velocidad: Aceleración Normalmente, la velocidad de un móvil varía durante su movimiento: a veces aumenta, otras disminuye y en ocasiones cambia de dirección. La aceleración representa la rapidez con que un móvil varía su velocidad. Es una magnitud vectorial. Se calcula dividiendo la variación de velocidad entre el intervalo de tiempo que ha transcurrido. v = velocidad (m/s) V 0 = velocidad inicial (m/s) t = tiempo (s) t 0 = tiempo inicial (s) Las unidades de la aceleración son m/s 2

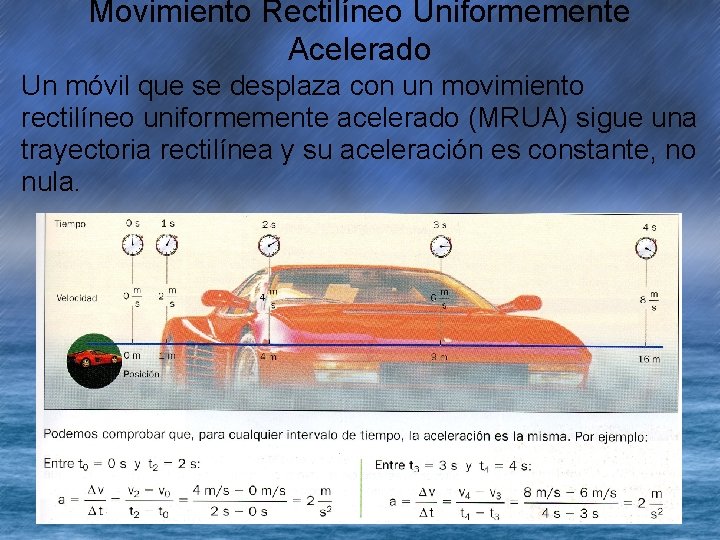
Movimiento Rectilíneo Uniformemente Acelerado Un móvil que se desplaza con un movimiento rectilíneo uniformemente acelerado (MRUA) sigue una trayectoria rectilínea y su aceleración es constante, no nula.

Movimiento Rectilíneo Uniformemente Acelerado Un cuerpo que soltamos y cae libremente tiene un MRUA ya que su aceleración es constante e igual a 9, 8 m/s 2 llamada aceleración de la gravedad. Es independiente de la masa del cuerpo

Movimiento Rectilíneo Uniformemente Acelerado En ciencias naturales es fundamental la: • Observación de un fenómeno natural, el • Registro de datos, la • Elaboración de gráficas y, a partir de ellas, la realización de un • Análisis para determinar la ley o • Modelo matemático que rige el comportamiento del fenómeno. • El tema se abordará a partir de un video (el cual se puede detener), a partir de él, se adquirirán datos de posición y su respectivo tiempo. • Con ellos se hará una tabulación de posición contra tiempo (x vs. t) • Se hará una gráfica de x vs. t • Se realizará una análisis gráfico con los conocimientos hasta ahora adquiridos del tema de movimiento rectilíneo uniforme (mru). • Ver video (mrua posición)

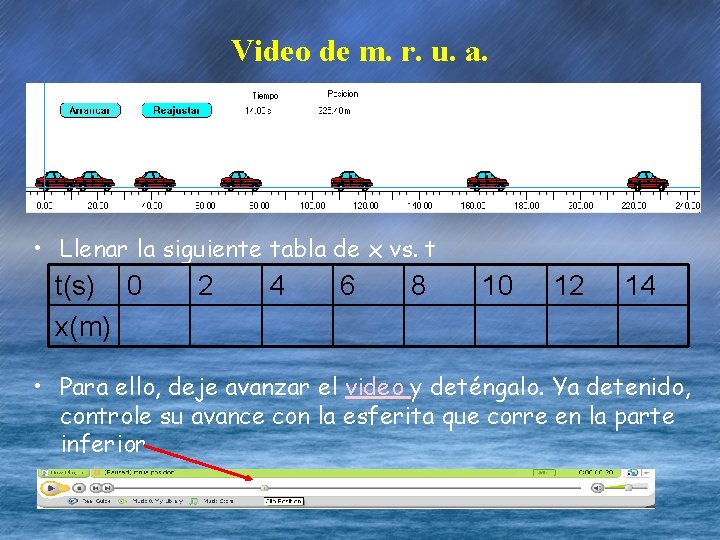
Video de m. r. u. a. • Llenar la siguiente tabla de x vs. t t(s) 0 x(m) 2 4 6 8 10 12 14 • Para ello, deje avanzar el video y deténgalo. Ya detenido, controle su avance con la esferita que corre en la parte inferior

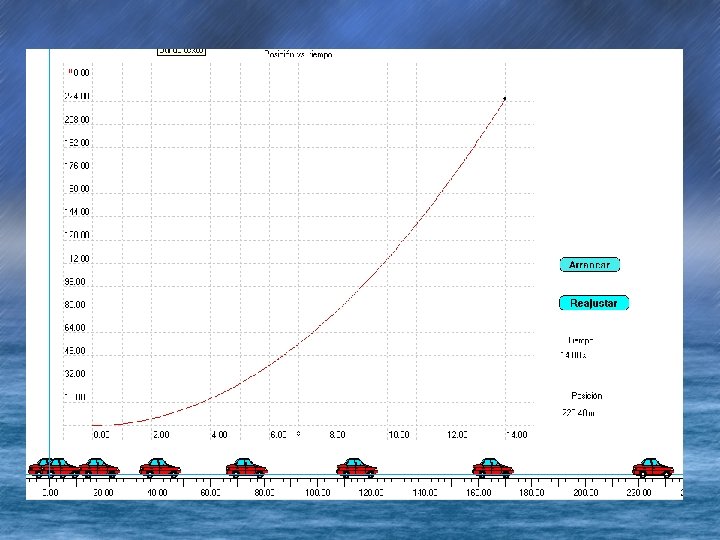
Tabulación de m. r. u. a. t(s) x(m) 0 0 2 4. 6 4 18. 4 6 41. 4 8 73. 6 10 115 12 14 165. 6 225. 4 • Realice la gráfica de x vs. t • Recuerde o revise como se realiza una gráfica – En que eje van las variables dependientes e independientes – Elegir una escala adecuada – Usar papel milimétrico – Etc.

Gráfica de posición vs. tiempo • Toda vez que realice su propia gráfica, siga el hipervínculo (posición vs. tiempo) donde se volverá a correr el video pero con su respectiva gráfica. • En la siguiente diapositiva se muestra la gráfica, (compárela con la que Usted obtuvo)

Análisis de datos Note que los intervalos de tiempo consecutivos son iguales: Dt = t 1 – t 0 = t 2 – t 1 = t 3 – t 2 = …. . t 7 – t 6 = 2 s y los respectivos desplazamientos: Dx = x 1 – x 0 = 4. 6 m – 0 m = 4. 6 m Dx = x 2 – x 1 = 18. 4 m - 4. 6 m = 13. 8 m Dx = x 3 – x 2 = 41. 4 m – 18. 4 m m = 23 m

Análisis de datos Dx = x 4 – x 3 = 73. 6 m – 41. 4 m = 32. 2 m Dx = x 5 – x 4 = 115. 0 m – 73. 6 m = 41. 4 m Dx = x 6 – x 5 = 165. 6 m – 115. 0 m = 50. 6 m Dx = x 7 – x 6 = 225. 4 m – 165. 6 m = 59. 8 m se puede observar que los cambios de posición en intervalos de tiempo de 2 s no son iguales, es decir el movimiento es rectilíneo no uniforme (recorre distancias diferentes en iguales intervalos de tiempo).

Análisis de datos En consecuencia las velocidades medias evaluadas en intervalos de tiempo distintos no serán constantes: . • Entre t 1 y t 0 • Entre t 2 y t 0 • Entre t 3 y t 0.

Análisis de datos • Entre t 4 y t 0 • Entre t 5 y t 0 • Entre t 6 y t 0

Velocidad instantánea Las velocidades medias representan la pendiente de la recta secante a la curva en los intervalos de tiempo considerados y sus respectivas posiciones. La información que proporciona la velocidad media solo es útil cuando el movimiento es rectilíneo uniforme. Como no es nuestro caso, se requiere generar un nuevo concepto: Velocidad instantánea El proceso para generarla es el siguiente. 1. En su gráfica elija un punto donde desee conocer la velocidad instantánea (por ejemplo a los 6 s) 2. Calcule la pendiente de la recta secante que une a ese punto que seleccionó y el último punto registrado en su gráfica (llámele vm 6)

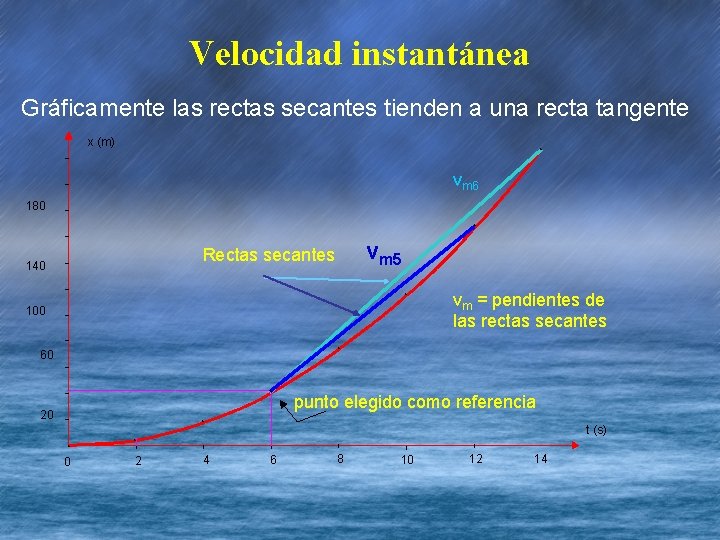
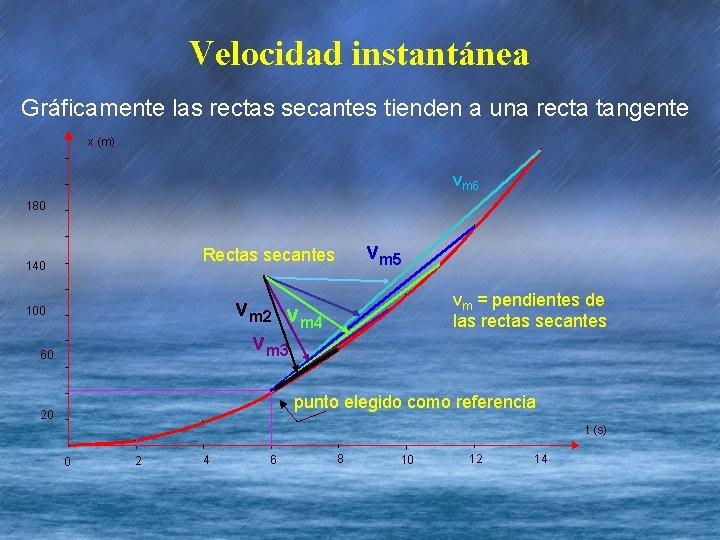
Velocidad instantánea Gráficamente las rectas secantes tienden a una recta tangente x (m) * vm 6 180 * vm 5 Rectas secantes 140 * 100 vm = pendientes de las rectas secantes * 60 * 20 punto elegido como referencia * * 0 * l 2 l 4 t (s) l l 6 8 10 12 14

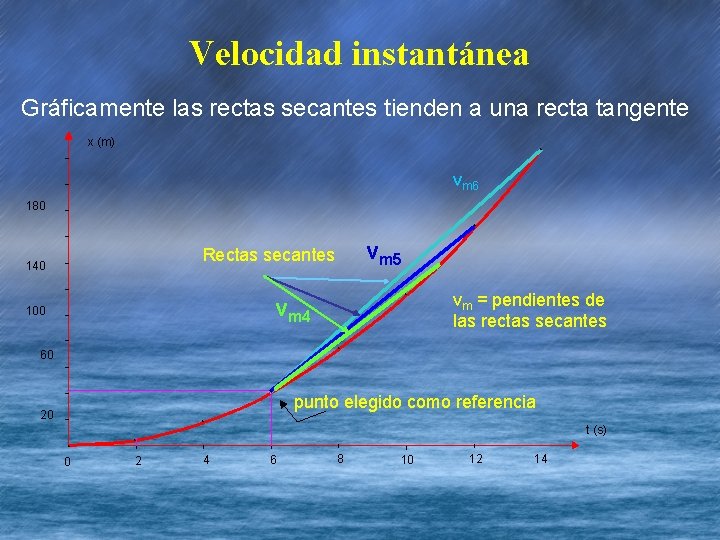
Velocidad instantánea Gráficamente las rectas secantes tienden a una recta tangente x (m) * vm 6 180 * vm 5 Rectas secantes 140 * vm 4 100 vm = pendientes de las rectas secantes * 60 * 20 punto elegido como referencia * * 0 * l 2 l 4 t (s) l l 6 8 10 12 14

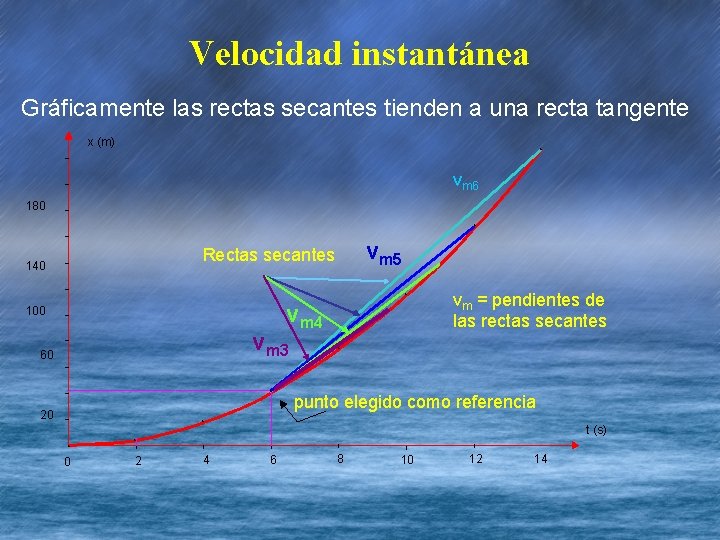
Velocidad instantánea Gráficamente las rectas secantes tienden a una recta tangente x (m) * vm 6 180 * vm 5 Rectas secantes 140 * vm 4 100 vm 3 60 * 20 vm = pendientes de las rectas secantes * punto elegido como referencia * * 0 * l 2 l 4 t (s) l l 6 8 10 12 14

Velocidad instantánea Gráficamente las rectas secantes tienden a una recta tangente x (m) * vm 6 180 * vm 5 Rectas secantes 140 vm 2 vm 4 vm 3 100 60 * 20 * vm = pendientes de las rectas secantes * punto elegido como referencia * * 0 * l 2 l 4 t (s) l l 6 8 10 12 14

Interpretación gráfica de la velocidad instantánea . x (m) * 180 * 140 * 100 Recta tangente * 60 20 * Punto elegido como referencia l l * * 0 *l 2 l 4 6 8 l 10 l 12 14 t (s)

Velocidad instantánea En función de sus cálculos, complete la siguiente tabla de v vs. t t (s) 0 2 4 6 8 10 12 14 v (m/s) Ir a hipervínculo rectas tangentes , subir pantalla dejando la proyección en el pizarrón. Los alumnos pasan al pizarrón trazan las tangentes auxiliándose de una regla, toman datos y realizar los cálculos para llenar la tabla. Nota al profesor: en la siguiente diapositiva se presenta la tabla

Velocidad instantánea • Usted debió aproximarse a los siguientes valores t (s) 0 2 4 6 8 10 12 14 v (m/s) 0 4. 6 9. 2 13. 8 18. 4 23 27. 6 32. 2 • Como podrá observar la velocidad cambia de instante a instante. La pregunta que surge es ¿Cómo cambia la velocidad?

Aceleración Media Para describir como cambia la velocidad v (t) se define el concepto de aceleración media: El cual nos indica cuan rápido es el cambio de velocidad en el intervalo de tiempo Sus unidades son

Aceleración Media De la misma forma que con el desplazamiento y la velocidad, se tiene que la aceleración también puede ser positiva o negativa, depende de: si vf > v 0 a > 0 acelerando si vf < v 0 a < 0 frenando si vf < v 0 a < 0 acelerando si vf > v 0 a > 0 frenando

Aceleración Media En algunas situaciones el valor de la aceleración media puede ser diferente sobre intervalos de tiempo distintos. Por ese motivo, es útil definir la aceleración instantánea: la aceleración también puede escribirse como Es decir, en un movimiento en línea recta, la aceleración es igual a la segunda derivada de la posición de la partícula con respecto al tiempo.

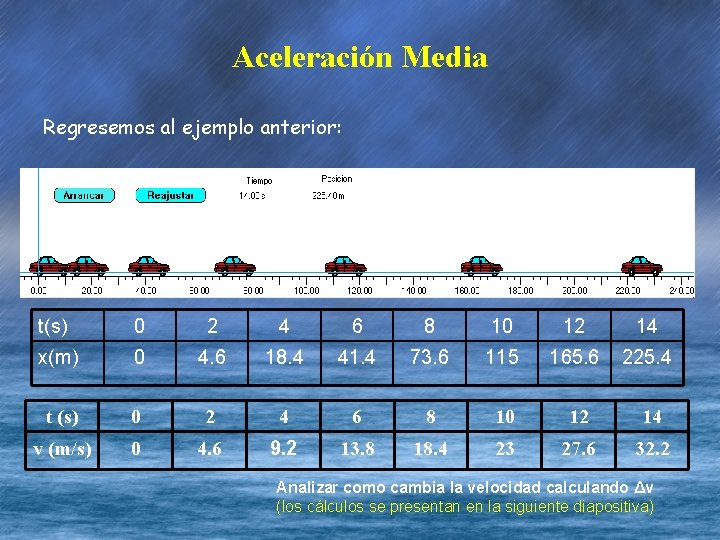
Aceleración Media Regresemos al ejemplo anterior: t(s) 0 2 4 6 8 10 12 14 x(m) 0 4. 6 18. 4 41. 4 73. 6 115 165. 6 225. 4 t (s) 0 2 4 6 8 10 12 14 v (m/s) 0 4. 6 9. 2 13. 8 18. 4 23 27. 6 32. 2 Analizar como cambia la velocidad calculando Δv (los cálculos se presentan en la siguiente diapositiva)

Aceleración Media Consideremos los cambios de velocidad • Entre t 2 y t 1 • Entre t 3 y t 2 • Entre t 4 y t 3 Dv = vf – v 0

Aceleración Media • Entre t 5 y t 4 • Entre t 6 y t 5 • Entre t 7 y t 6

Aceleración Media Y las correspondientes aceleraciones medias • Entre t 2 y t 1 • Entre t 3 y t 2 • Entre t 4 y t 3

Aceleración Media Si evaluamos la aceleración media en los demás intervalos de tiempo la encontraremos igual a Este tipo de movimiento se conoce como: Rectilíneo Uniformemente Acelerado (MRUA) o con Aceleración Constante

Gráficas del MRUA t(s) 0 2 4 6 8 10 12 14 x(m) 0 4. 6 18. 4 41. 4 73. 6 115 165. 6 225. 4 t (s) 0 2 4 6 8 10 12 14 v (m/s) 0 4. 6 9. 2 13. 8 18. 4 23 27. 6 32. 2 Los alumnos realizan gráfica v vs. t y se retroalimentan con la diapositiva siguiente

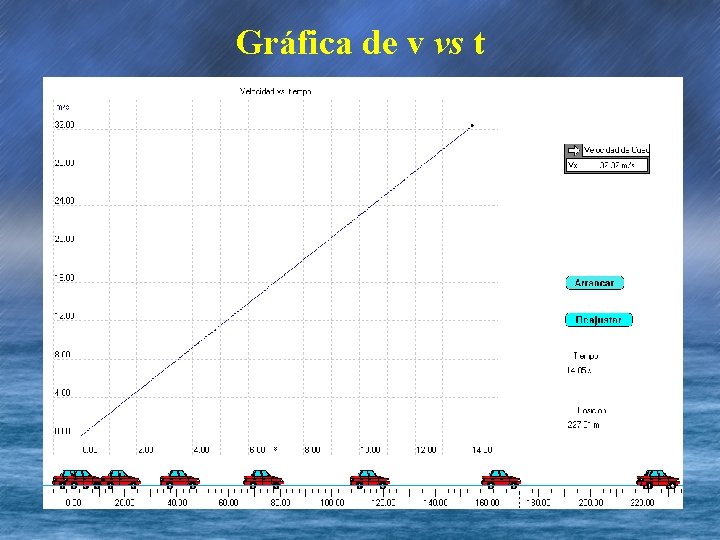
Gráfica de v vs t

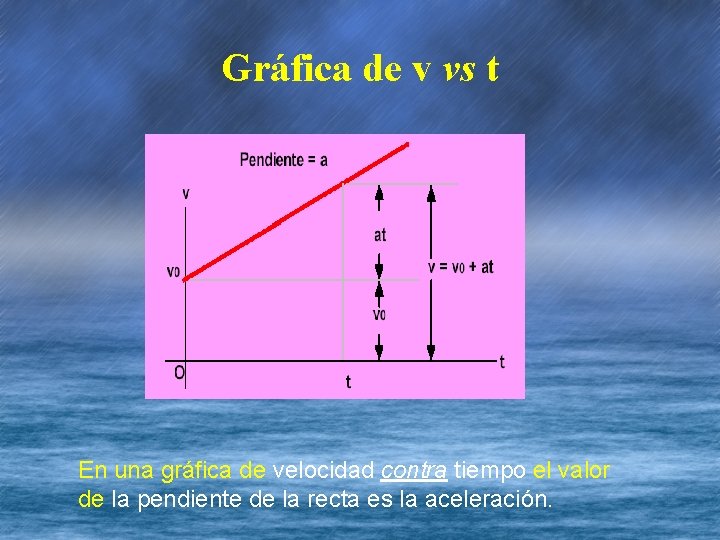
Gráfica de v vs t En una gráfica de velocidad contra tiempo el valor de la pendiente de la recta es la aceleración.

Ecuaciones de M R U A La ecuación de la posición x = x(t) que describe el movimiento con aceleración constante, puede ser obtenida al considerar que para este movimiento en particular la velocidad media (promedio) en cualquier intervalo de tiempo coincide con la media aritmética de la velocidad inicial, v 0 y de la velocidad final v, es decir : Velocidad media igualando Despejando velocidad media aritmética

Ecuaciones de M R U A Teniendo en cuenta que v = v 0 + at , se puede sustituir en Desarrollando queda: Lo que nos indica la grafica x vs t es una sección de parábola (En cursos de matemáticas sería de la forma y = a + bx + cx 2)

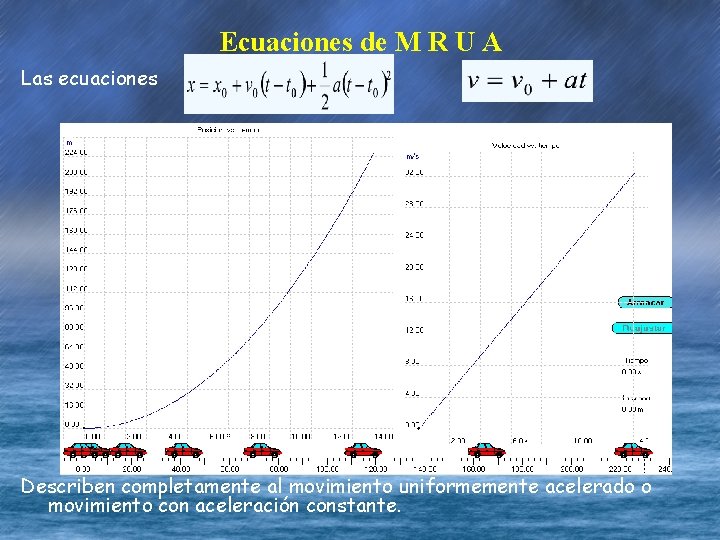
Ecuaciones de M R U A Las ecuaciones Describen completamente al movimiento uniformemente acelerado o movimiento con aceleración constante.

Ecuaciones de M R U A Sin embargo es posible obtener a partir de éstas un par de ecuaciones mas: • Una de ellas relaciona el cambio de la posición con el cambio de velocidad y la aceleración. En ausencia del tiempo: • En la otra nos relaciona el cambio de la posición con velocidad y el tiempo, pero en ausencia de la aceleración:

Resumen de Ecuaciones de M R U A Modelo matemático Información adicional x = x 0 + v 0 t + ½ at 2 No contiene la velocidad final x = x 0 + ½(v + v 0)t No contiene la aceleración x = x 0 + vt - ½ at 2 No contiene la velocidad inicial v = v 0 + at No contiene la posición v 2 – v 02 = 2 a(x-x 0) No contiene el tiempo x = x 0 + vt - ½ at 2 No contiene la velocidad inicial

Simulación de problemas de libro de texto • • • Resnick sec. 2 -6 problema 35 Resnick sec. 2 -6 problema 36 Resnick sec. 2 -6 problema 38 Resnick sec. 2 -6 problema 45 Resnick sec. 2 -6 problema 47

Tarea de M R U A Tarea de Movimiento Rectilíneo Uniformemente Acelerado Fecha de entrega: Asesorías: Talleres extracurriculares: Ligas de interés: