Chronikis a language for Bayesian timeseries models Kevin

Chronikis: a language for Bayesian time-series models Kevin S. Van Horn | Senior Data Science Engineer © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential.

English: time series. Greek: χρονική σειρά http: //chronikis. org or http: //xronikis. org © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 2

Chronikis is… § § § A language for defining statistical time-series models A compiler that generates code for model estimation and prediction An R package of utility functions © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 3

Implementation Notes § § Compiler § Written in Haskell § Target: Stan model for estimation (. stan) § Target: source-able R code to create DLMs from estimated parameters R package § Call compiler and Stan from R § Fit model § Forecast § Built on dlm package © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 4

Statistical time-series models § © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 5

Dynamic Linear Models (DLMs) AKA linear Gaussian State Space Models ssm(Z, H, T, Q, a 0, P 0) © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 6
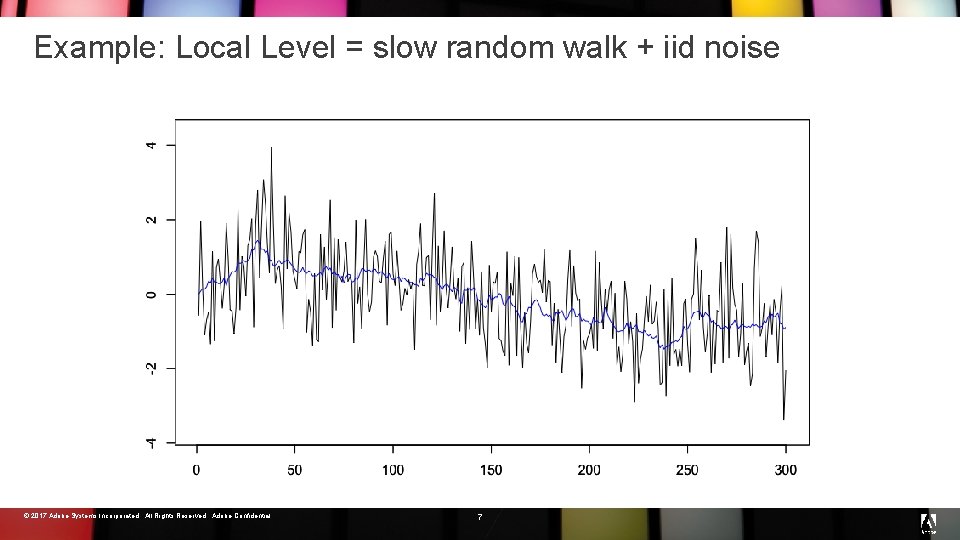
Example: Local Level = slow random walk + iid noise © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 7

Example: Local Level def main(mu 0: real, sigma 0: real{0. 0, }, scale_rw, scale_err: real{0. 0, }) = white noise: zero-mean iid sigma_rw ~ half_cauchy(scale_rw); Gaussian sigma_err ~ half_cauchy(scale_err); accum(wn(sigma_rw), mu 0, sigma 0) + wn(sigma_err) Cumulative sums of draw from argument. © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 8

Example: Local Level def main(mu 0: real, sigma 0: real{0. 0, }, scale_rw, scale_err: real{0. 0, }) = sigma_rw ~ half_cauchy(scale_rw); sigma_err ~ half_cauchy(scale_err); accum(wn(sigma_rw), mu 0, sigma 0) + wn(sigma_err) © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 9

Example: Local Level def main(mu 0: real, sigma 0: real{0. 0, }, scale_rw, scale_err: real{0. 0, }) = sigma_rw ~ half_cauchy(scale_rw); sigma_err ~ half_cauchy(scale_err); accum(wn(sigma_rw), mu 0, sigma 0) + wn(sigma_err) © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 10

Example: Local Level def main(mu 0: real, sigma 0: real{0. 0, }, scale_rw, scale_err: real{0. 0, }) = sigma_rw ~ half_cauchy(scale_rw); sigma_err ~ half_cauchy(scale_err); accum(wn(sigma_rw), mu 0, sigma 0) + wn(sigma_err) © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 11
![data { int<lower = 1> N; vector[N] y; real mu 0_; real<lower = 0. data { int<lower = 1> N; vector[N] y; real mu 0_; real<lower = 0.](http://slidetodoc.com/presentation_image_h2/f26c6aeb912ca095c13e193582e0e646/image-12.jpg)
data { int<lower = 1> N; vector[N] y; real mu 0_; real<lower = 0. 0> sigma 0_; real<lower = 0. 0> scale_rw_; real<lower = 0. 0> scale_err_; } transformed data { matrix[1, N] yy = to_matrix(y'); vector[1] Z_0_ = rep_vector(1. 0, 1); matrix[1, 1] T_0_ = rep_matrix(1. 0, 1, 1); vector[1] a 0_0_ = rep_vector(mu 0_, 1); matrix[1, 1] P 0_0_ = rep_matrix(square(sigma 0_), 1, 1); } parameters { real<lower = 0. 0> raw_0_; real<lower = 0. 0> raw_1_; } transformed parameters { real sigma_rw_ = raw_0_ * scale_rw_; real sigma_err_ = raw_1_ * scale_err_; } model { real H_0_ = square(sigma_err_); matrix[1, 1] Q_0_ = rep_matrix(square(sigma_rw_), 1, 1); raw_0_ ~ cauchy(0. 0, 1. 0) T[0. 0, ]; raw_1_ ~ cauchy(0. 0, 1. 0) T[0. 0, ]; yy ~ gaussian_dlm_obs(to_matrix(Z_0_), T_0_, rep_vector(H_0_, 1), Q_0_, a 0_0_, P 0_0_); } © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 12
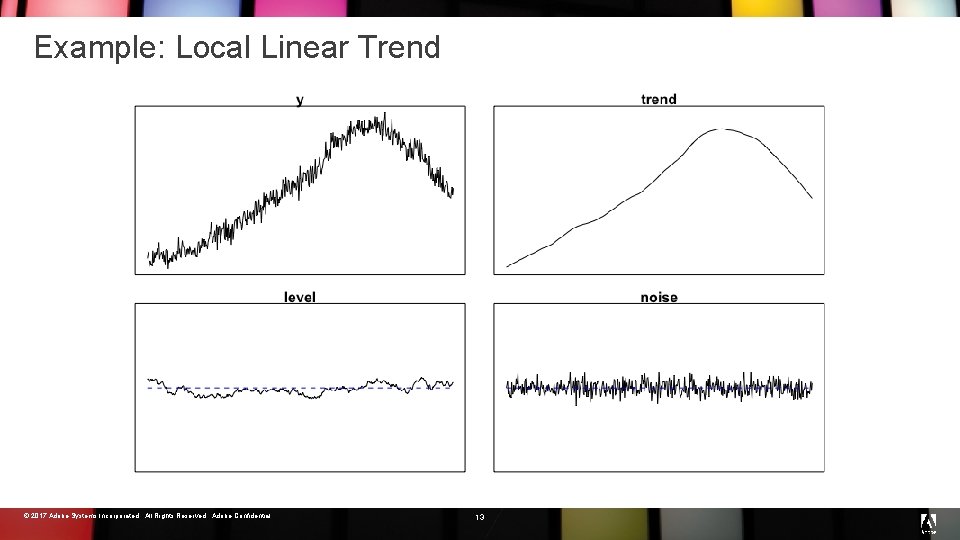
Example: Local Linear Trend © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 13

Example: Local Linear Trend def main(mu 0: real, sigma 0: real{0. 0, }, scale_l 0, scale_t 0: real{0. 0, }) = phi_l ~ uniform(0. 0, 1. 0); phi_t ~ uniform(0. 0, 1. 0); sigma_err ~ half_cauchy(scale_err); sigma_l 0 ~ half_cauchy(scale_l 0); sigma_t 0 ~ half_cauchy(scale_t 0); sigma_l = sqrt(1 – phi_l^2) * sigma_l 0; sigma_t = sqrt(1 - phi_t^2) * sigma_t 0; accum(ar 1(phi_t, sigma_t 0), mu 0, sigma 0) + ar 1(phi_l, sigma_l 0) + wn(sigma_err) © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 14 trend level noise

Example: Local Linear Trend def main(mu 0: real, sigma 0: real{0. 0, }, scale_l 0, scale_t 0: real{0. 0, }) = phi_l ~ uniform(0. 0, 1. 0); phi_t ~ uniform(0. 0, 1. 0); sigma_err ~ half_cauchy(scale_err); sigma_l 0 ~ half_cauchy(scale_l 0); sigma_t 0 ~ half_cauchy(scale_t 0); sigma_l = sqrt(1 – phi_l^2) * sigma_l 0; sigma_t = sqrt(1 - phi_t^2) * sigma_t 0; accum(ar 1(phi_t, sigma_t 0), mu 0, sigma 0) + ar 1(phi_l, sigma_l 0) + wn(sigma_err) © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 15

Example: Local Linear Trend def main(mu 0: real, sigma 0: real{0. 0, }, scale_l 0, scale_t 0: real{0. 0, }) = phi_l ~ uniform(0. 0, 1. 0); phi_t ~ uniform(0. 0, 1. 0); sigma_err ~ half_cauchy(scale_err); sigma_l 0 ~ half_cauchy(scale_l 0); sigma_t 0 ~ half_cauchy(scale_t 0); sigma_l = sqrt(1 – phi_l^2) * sigma_l 0; sigma_t = sqrt(1 - phi_t^2) * sigma_t 0; accum(ar 1(phi_t, sigma_t 0), mu 0, sigma 0) + ar 1(phi_l, sigma_l 0) + wn(sigma_err) © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 16

Compiler Stages Parse Type inference Transformations 1. 2. 3. 4. 5. 6. 1. expansions: ssm(Z, H, T, Q, a 0, P 0) 2. optimizations Infer array shapes, parameter bounds. Create Stan AST (assign vars to blocks) Print Stan AST © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 17
© 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 18
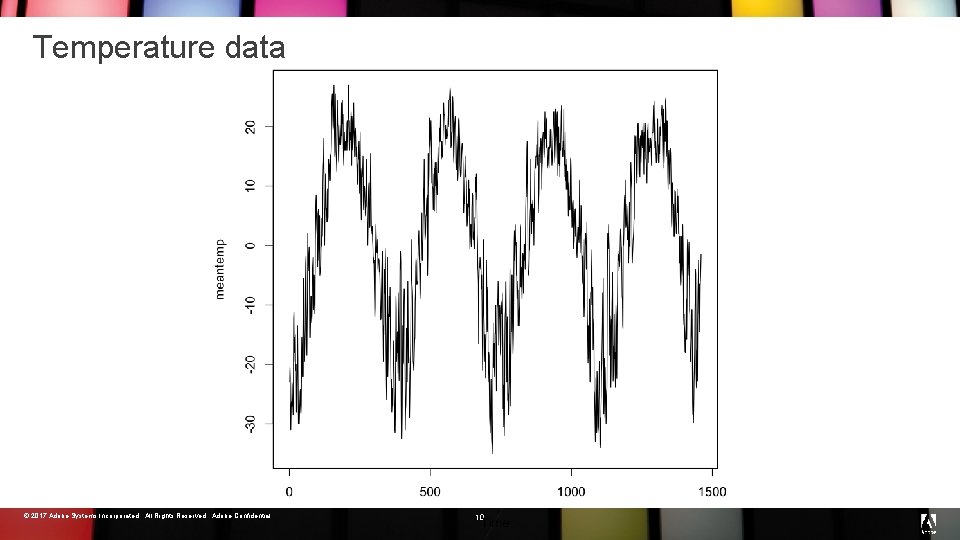
Temperature data © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 19

Temperature Model with Yearly Periodicity © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 20
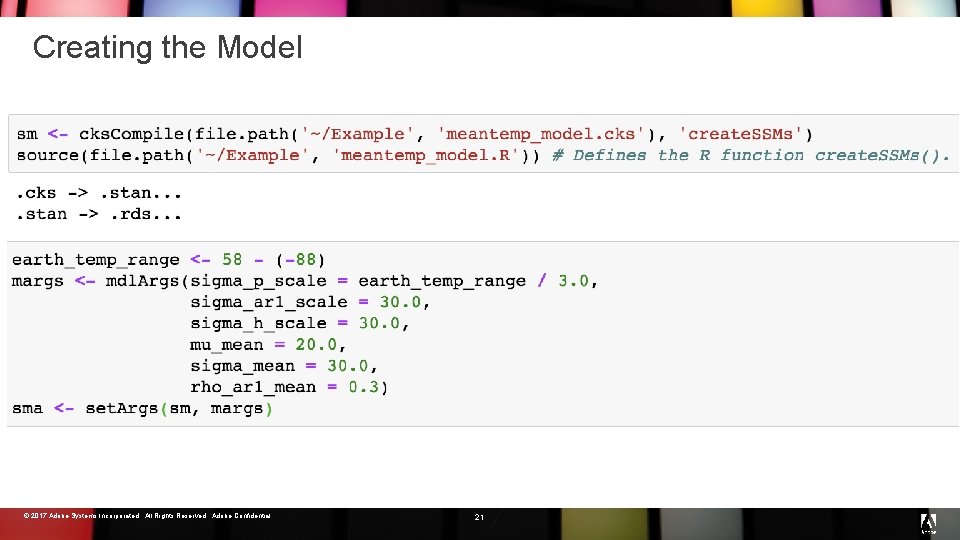
Creating the Model © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 21
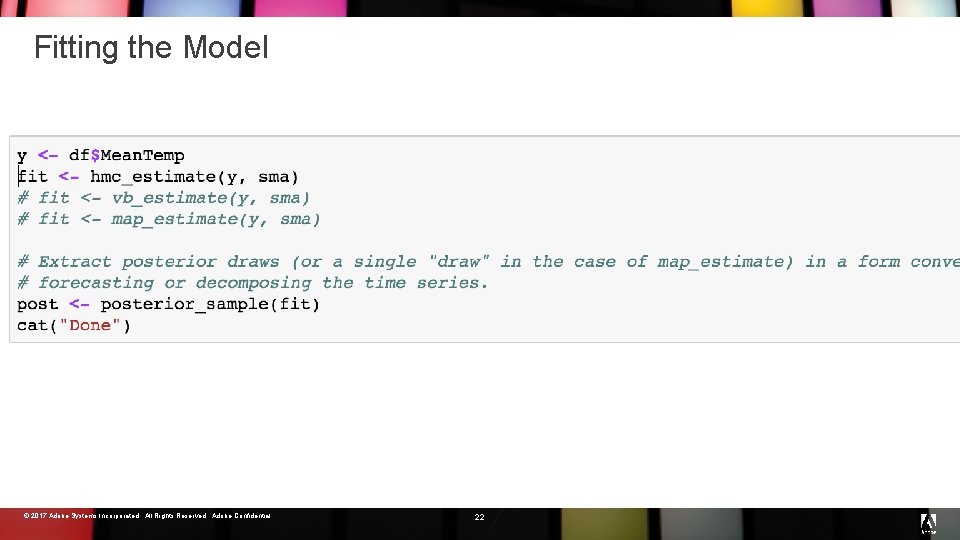
Fitting the Model © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 22
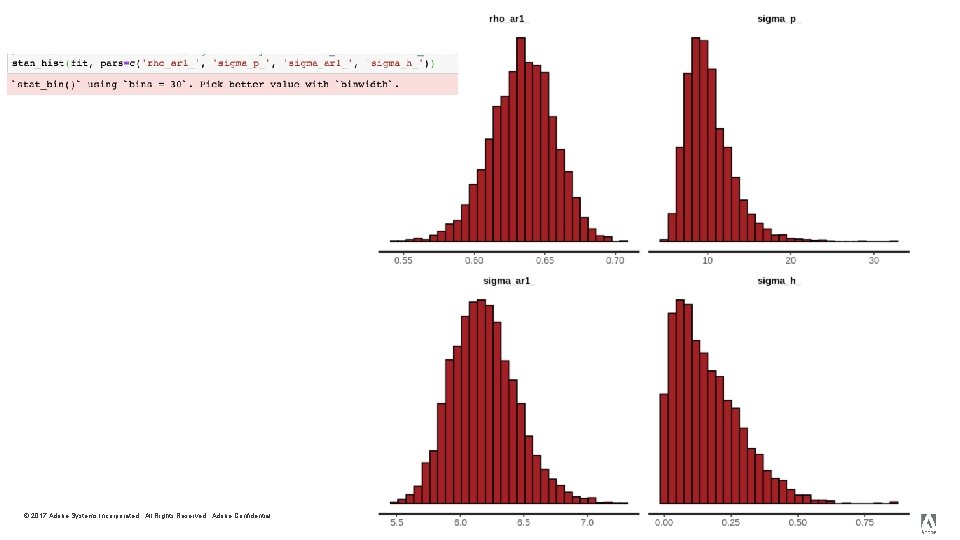
© 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 23

Forecasting © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 24
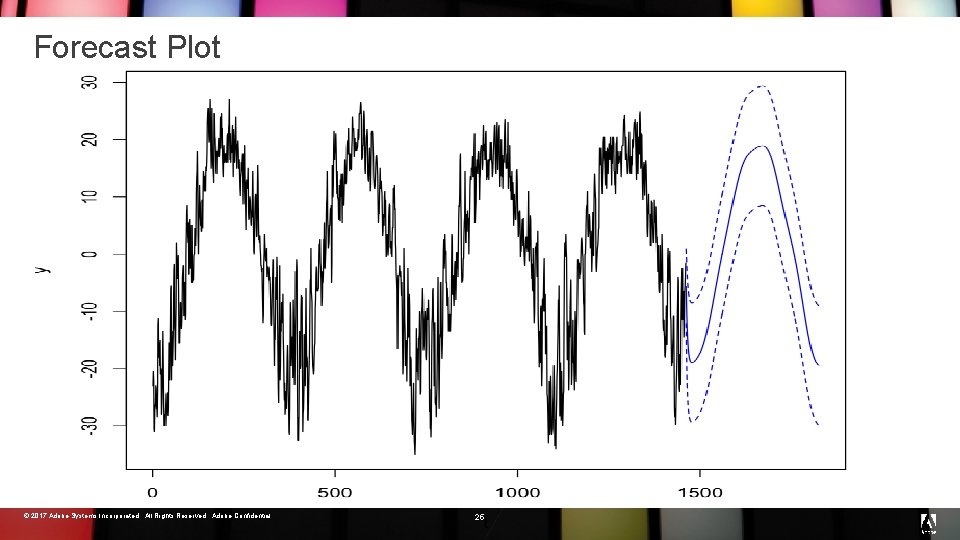
Forecast Plot © 2017 Adobe Systems Incorporated. All Rights Reserved. Adobe Confidential. 25

- Slides: 26