Chromatography Introduction GENERAL THEORY OF COLUMN CHROMATOGRAPHY Introduction

Chromatography : Introduction GENERAL THEORY OF COLUMN CHROMATOGRAPHY

Introduction • Of the two methods for bringing the stationary and mobile phases into contact, the more important is column chromatography. • In this section we develop a general theory that we may apply to any form of column chromatography. • With appropriate modifications, this theory also can be applied to planar chromatography.

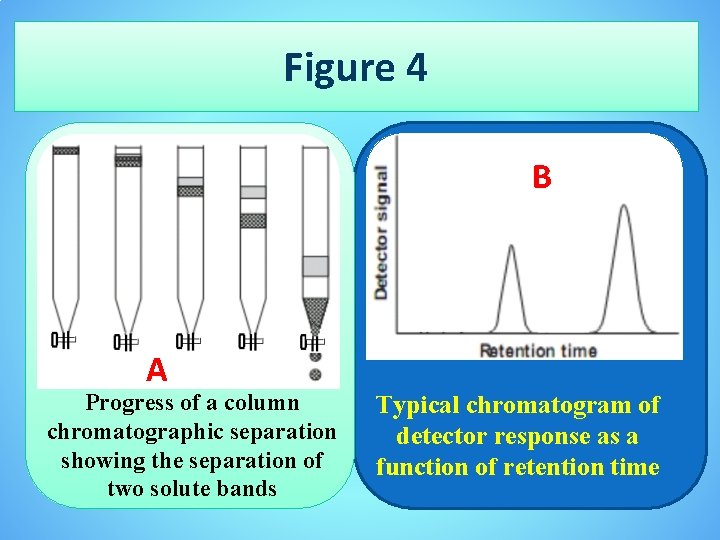
• A typical column chromatography is shownin Figure 4. • The sample is introduced at the top of the column as a narrow band. Ideally, the solute’s initial concentration profile is rectangular (Figure 4 a). • As the sample moves down the column the solutes begin to separate, and the individual solute bands begin to broaden and develop a Gaussian profile (Figures 4 b, c). I • f the strength of each solute’s interaction with the stationary phase is sufficiently different, then the solutes separate into individual bands (Figure 4 d). • The progress of a chromatographic separation is monitored with a suitable detector situated at the end of the column.

Figure 4 B A Progress of a column chromatographic separation showing the separation of two solute bands Typical chromatogram of detector response as a function of retention time

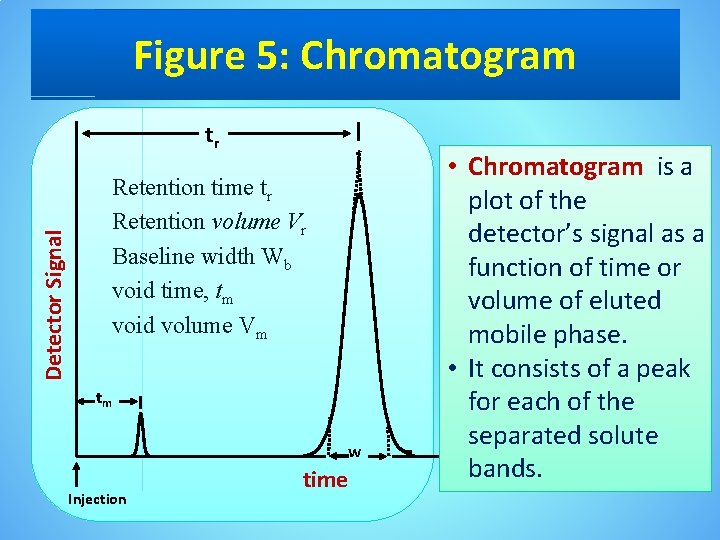
Figure 5: Chromatogram tr Detector Signal Retention time tr Retention volume Vr Baseline width Wb void time, tm void volume Vm tm w Injection time • Chromatogram is a plot of the detector’s signal as a function of time or volume of eluted mobile phase. • It consists of a peak for each of the separated solute bands.

The retention time • A chromatographic peak may be characterized in many ways, two of which are shown in Figure 5. • The retention time, tr , is the elapsed time from the introduction of the solute to the peak maximum. • The retention time also can be measured indirectly as the volume of mobile phase eluting between the solute’s introduction and the appearance of the solute’s peak maximum. This is known as the retention volume, Vr. • Dividing the retention volume by the mobile phase’s flow rate, u, gives the retention time.

Baseline width • The second important parameter is the chromatographic peak’s width at the baseline, w. • Baseline width is determined by the intersection with the baseline of tangent lines drawn through the inflection points on either side of the chromatographic peak. • Baseline width is measured in units of time or volume, depending on whether the retention time or retention volume is of interest.

Void time • Besides the solute peak, Figure 5 also shows a small peak eluted soon after the sample is injected into the mobile phase. • This peak results from solutes that move through the column at the same rate as the mobile phase. • Since these solutes do not interact with the stationary phase, they are considered non-retained. • The time or volume of mobile phase required to elute nonretained components is called the column’s void time (or dead time or hold up time), tm (t 0) , or void volume (V 0).

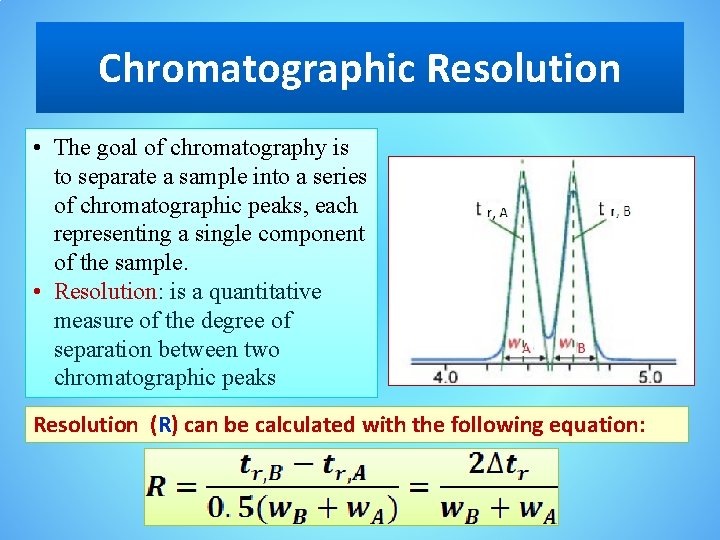
Chromatographic Resolution • The goal of chromatography is to separate a sample into a series of chromatographic peaks, each representing a single component of the sample. • Resolution: is a quantitative measure of the degree of separation between two chromatographic peaks Resolution (R) can be calculated with the following equation:

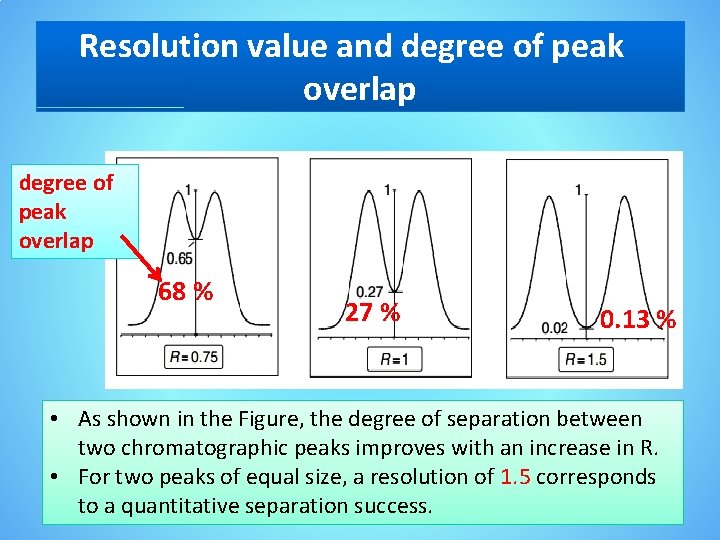
Resolution value and degree of peak overlap 68 % 27 % 0. 13 % • As shown in the Figure, the degree of separation between two chromatographic peaks improves with an increase in R. • For two peaks of equal size, a resolution of 1. 5 corresponds to a quantitative separation success.

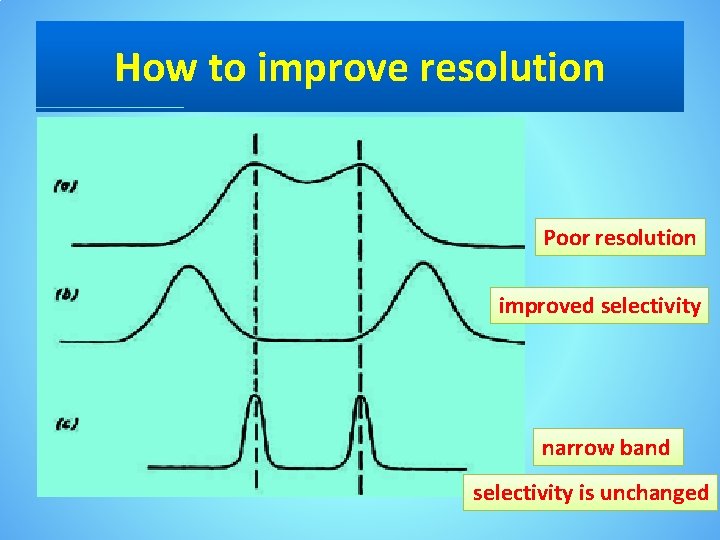
How to improve resolution Poor resolution improved selectivity narrow band selectivity is unchanged

How to improve resolution • From later equation, it is clear that resolution may be improved either by increasing ∆tr or by decreasing w. A or w B. • We can increase ∆tr by enhancing the interaction of the solutes with the column or by increasing the column’s selectivity for one of the solutes. • Peak width is a kinetic effect associated with the solute’s movement within and between the mobile phase and stationary phase. • The effect is governed by several factors that are collectively called column efficiency.

COLUMN EFFICIENCY • At the beginning of a chromatographic separation the solute occupies a narrow band of finite width. • As the solute passes through the column, the width of its band continually increases in a process called band broadening. • Column efficiency provides a quantitative measure of the extent of band broadening.

PLATE THEORY OF CHROMATOGRAPHY • Resolution is a measure of the efficiency of the column. • There another parameter which defines the efficiency as the number of theoretical plates, N. • Consider a column that is divided into N segments of equal length, and that each segment is just long enough to allow complete equilibration of solute partitioning between the stationary phase and the mobile phase, according to its partition coefficient. Each of these segments is called a theoretical plate. . • It is important to remember that a theoretical plate is an artificial construct and that no such plates exist in a chromatographic column.

The relationship between column length, number and height of theoretical plates • The relationship between column length (L), number of theoretical plates, N, and the height of a theoretical plate, H; are give by the following equation; • The greater the number of plates for a given column length, the shorter the height equivalent to a theoretical plate, H, and the more efficiently the column. • A column’s efficiency improves with an increase in the number of theoretical plates or a decrease in the height of a theoretical plate.

Calculation of number of theoretical plates • The number of theoretical plates in a chromatographic column is obtained by using the following equations: • An advantage of N as a measure of efficiency is that – it may be calculated from measurements on a single peak. Unlike Rs, it does not require a pair of peaks and is independent of their relative selectivity . – It may be calculated using either the peak width at base, wb, or peak width at half the peak height, wh. – The latter (wh) is sometimes better, whenfor broadened peak, fronting or the effects of adsorption (tailing).

Notes on the number of theoretical plates • A ‘‘good’’ column will have large N values (104 ->105), and a small HETP. • Columns packed with a small-particle stationary phase have been shown to yield higher N values than those packed with larger particles. • In fact, the number of theoretical plates depends on both the properties of the column and the solute. • As a result, the number of theoretical plates for a column is not fixed and may vary from solute to solute.

Capacity factor • The length of time it takes a retarded compound to pass through the column depends on its capacity factor (K'). • It is a measure of how strongly a solute is retained by the stationary phase (k'), which is a measure of the degree with which it partitions (adsorbs) into the stationary phase from the mobile phase: tm is the retention time of the non retained compound t`r Adjusted retention time (t'r) Is the difference between a solute’s retention time and column’s void time (dead time). t'r = tr – tm

Significance of K` Capacity factor Results k` = 0 a component is unretained k` < 2 all peaks are packed together too closely at the beginning of the chromatogram. k` is between 2 and about 10 good separations are observed k` > 10 peaks are separated, but they take too long to elute, have become wider and lower,

Selectivity factor • The relative selectivity of a chromatographic column for a pair of solutes is given by the selectivity factor, a, which is defined as • The identities of the solutes are defined such that solute A always has the smaller retention time. • Accordingly, the selectivity factor is equal to 1 when the solutes elute with identical retention times, and is greater than 1 when t r, A is greater than t r, B

Peak asymmetry • Another situation which may lead to poor integrator performance is where peaks are tailing and thus have a high element of asymmetry. The expression used to assess this is: Asymmetry factor (AF) = b/a • where a is the leading half of the peak measured at 10% of the peak height and b is the trailing half of the peak measured at 10% of the peak height. Figure 8

Ideal value of AF • The ideal value of Asymmetry factor is in the range 0. 95 -1. 15. • The peak in Figure 8 A has an asymmetry factor of 0. 97 indicates good asymmetry while • The peak in Figure 8 B has an asymmetry factor of 1. 77 and is thus tailing quite badly; • The most common cause of tailing is due to adsorption of the analyte onto active sites in the chromatographic column.

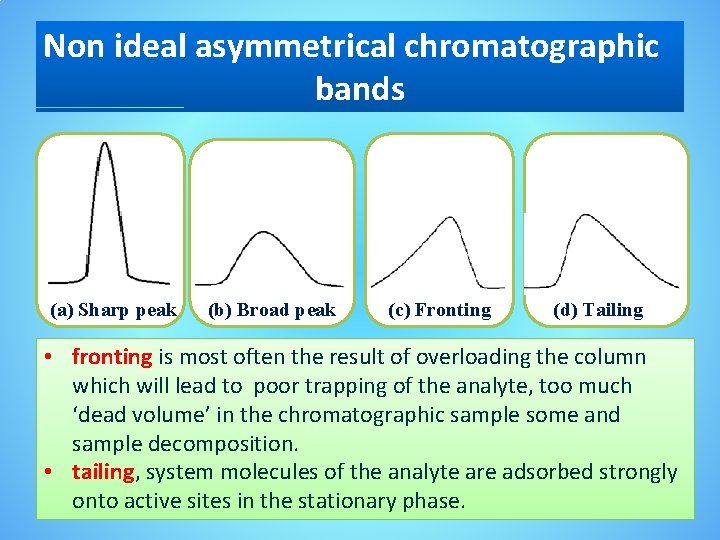
Non ideal asymmetrical chromatographic bands (a) Sharp peak (b) Broad peak (c) Fronting (d) Tailing • fronting is most often the result of overloading the column which will lead to poor trapping of the analyte, too much ‘dead volume’ in the chromatographic sample some and sample decomposition. • tailing, system molecules of the analyte are adsorbed strongly onto active sites in the stationary phase.