CHP 4 QUEUE 1 INTRODUCTION A queue is

CHP 4 QUEUE

1. INTRODUCTION ØA queue is a linear list in which elements can be added at one end and elements can be removed only at other end. ØThat is, the first element added to the queue is the first element to be removed. ØQueue works on the principle of ‘ first in first out’(FIFO). ØA common example of queue is people waiting in line at ticket window.

2. DEFINITION AND TYPES A queue is a linear data structure in whichanewelement is inserted at one end and element is deleted from other end. The end of the queue from which the element is deleted is known as front. The end at which new element is added is known as rear. Fig. 4. 1 shows a queue. v. TYPES OF QUEUE: 1. CIRCULAR QUEUE 2. DEQUEUE 3. PRORITY QUEUE

3. OPERATIONS ON QUEUE q. The two basic operations that can be performed on a queue are: Insert : to insert an element at rear of the queue Delete: to delete an element from front of the queue. q. Before inserting a new element in the queue, it is necessary to test the condition of overflow. q. Overflow occurs when the queue is full and there is no space for a new element. q Similarly, before removing the element from the queue, it is necessary to check the condition of underflow. q Underflow occurs when the queue is empty.

4. MEMORY REPRESENTATION OFQUEUES A queue can be represented in memory either as an array or as a singly linked list.

INSERTOPERATIONS ON QUEUE

DELETE OPERATIONS ON QUEUE

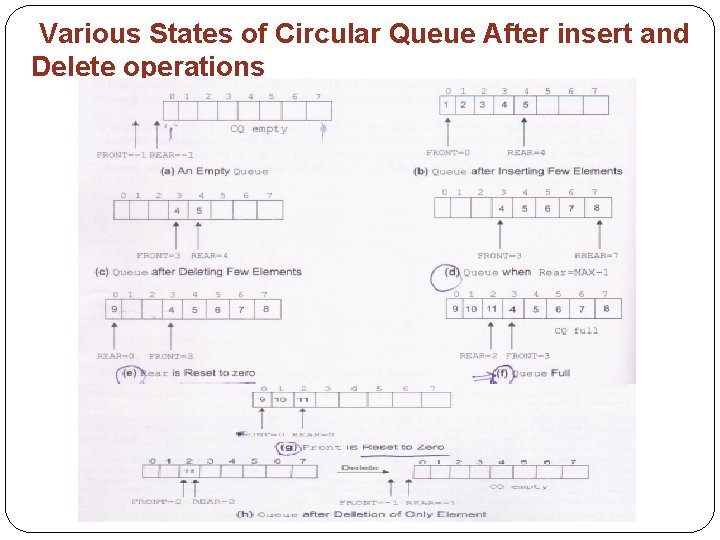
5. CIRCULAR QUEUE � As discussed earlier, in case of queue represented as an array, once the value of the rear reaches the maximum size of the queue, no more elements can be inserted. � However, there may be the possibility that space on the left of the front index is vacant. Hence, in spite of space on the left of front being empty, the queue is considered to be full. � This wastage of space in the array implementation of a queue can be avoided by shifting the elements to the beginning of array if the space is available. � In order to do this, the values of Rear and Front indices have to be changed accordingly. However, this is a complex process and is difficult to be implemented. An alternative solution to this problem is to implement a queue as a circular queue. � The array implementation of circular queue is similar to the array implementation of queue. The only difference is that as soon as the rear index of the queue reaches the maxi mumsize of the array, Rear is reset to the beginning of the queue provided it is free. The circular queue is full only when all the locations in the array are occupied. The circular queue is shown in Figure 4. 3.

Various States of Circular Queue After insert and Delete operations

Number of Elements in Circular Queue � The total number of elements in a circular queue at any point of time can be calculated from the current values of the Rear and the Front indices of the queue. � In case, Front<Rear, the total number of elements = Rear Front+1. For instance, in Fig ure 4. 5(a), Front=3 and Rear=7. � Hence, the total number of elements in CQueue at this point of time is 7 3+1=5. � In case, Front>Rear, the total number of elements = Max+ (Rear Front) +1. For instance, in Figure 4. 5(b), Front=3 and Rear=0. Hence, the total number of elements in CQueue is 8+(0 3)+l.

Algorithm of Circular Queue

Algorithm of Circular Queue

6. PRIORITY QUEUE � A priority queue is a type of queue in which each element is assigned a priority and the elements are added or removed according to that priority. While implementing a priority queue, following two rules are applied. (1)The element with higher priority is processed before any element of lower priority. (2)The elements with the same priority are processed according to the order in which they were added to the queue. � A priority queue can be represented in many ways. Here, we are discussing multi queue implementation of priority queue.

Multi-queue Implementation (Array Representation of Priority Queue) �In multi queue representation of priority queue, for each priority, a queue is maintained. The queue corresponding to each priority can be represented in the same array of sufficient size. �For each queue, two variables Fronti and Reari are maintained (see Figure 4. 6). �Observe that Fronti and Reari correspond to the front and rear position of queue for priority Priorityi.

� Clearly, in this representation, shifting is required to make space for an element to be inserted. � To avoid this shifting, an alternative representation can be used (see Figure 4. 7). � In this representation, instead of representing queue corresponding to each priority using a single array, a separate array for each priority is maintained. � Each queue is implemented as a circular array and has its own two variables, Front and Rear. � The element with given priority number is inserted in the corresponding queue. Similarly, whenever an element is to be deleted from the queue, it must be the element from the highest priority queue. � Note that lower priority number indicates higher priority.

�If the size of each queue is same, then instead of multiple one dimensional arrays, a single two dimensional array can be used where row i corresponds to the queue of priority i. �In addition, two single dimensional arrays are used. One is used to keep track of front position and another to keep track of rear position of each queue (see Figure 4. 8).

INSERT OPERATION IN PRIORITY QUEUE

DELETE OPERATION IN PRIORITY QUEUE