Choosing the right test Mathematics Statistics Help University




















- Slides: 41

Choosing the right test Mathematics & Statistics Help University of Sheffield

Learning outcomes • By the end of this session you should know about: – Some useful approaches to analysing data • By the end of this session you should be able to: – Recognise different data types – Use a flowchart to decide which analysis method to use – Undertake some basic analyses and construct appropriate charts for your data

Some initial thoughts

Planning a study • What do you want to investigate and why? What are your aims? • How are you going to investigate it? • How will you collect your data? • Who/what is in the sample? • How will you summarise your data? • How will you analyse your data?

Steps for choosing the right test (1) • • Clearly define your research question What is your main outcome of interest? There may be more than one. What data type is it? The data type will determine the type of analysis Are the observations paired? Can it be characterised using a known distribution (i. e. parametric vs non-parametric test)? • What may affect the outcome of interest? What data type is it/are they? • • How will your results be summarised? What charts can you use to display your results?

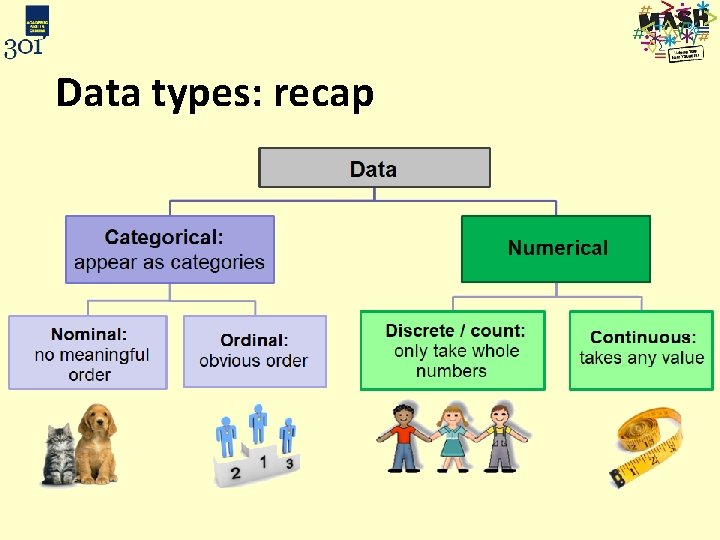
Data types: recap

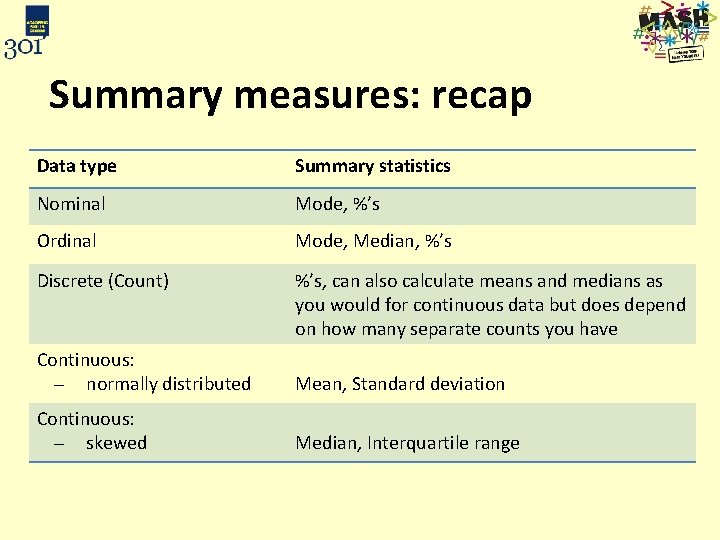
Summary measures: recap Data type Summary statistics Nominal Mode, %’s Ordinal Mode, Median, %’s Discrete (Count) %’s, can also calculate means and medians as you would for continuous data but does depend on how many separate counts you have Continuous: normally distributed Mean, Standard deviation Continuous: skewed Median, Interquartile range

Chart types: recap • One variable − Categorical: Pie chart, barchart − Numerical discrete: barchart − Numerical continuous: histogram, boxplots • Two variables − Both categorical: stacked barchart, clustered barchart, multiple pie charts − One categorical / one numerical discrete: boxplots (sometimes!), multiple barcharts − One categorical / one numerical continuous: boxplots, multiple histograms − Both numerical: scatterplot

Steps for choosing the right test (2) • Are you interested: Testing differences between groups. How many groups are there? Assessing/modelling the relationship between variables • Are the observations paired? Is the pairing due to having repeated measurements of the same variable for each subject? • Does the test you have chosen make any assumptions? Are the assumptions met? e. g. assumption of normality for t-test

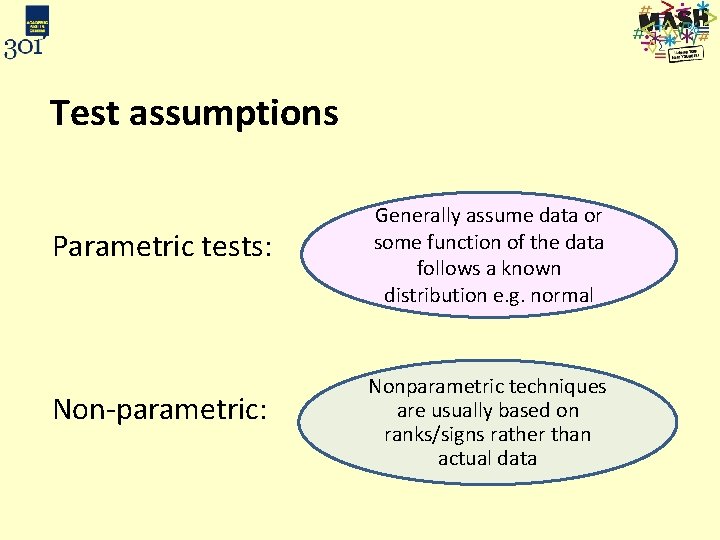
Test assumptions Parametric tests: Non-parametric: Generally assume data or some function of the data follows a known distribution e. g. normal Nonparametric techniques are usually based on ranks/signs rather than actual data

Non-parametric methods are used when: – Dependent variable is ordinal – A plot of the data appears to be very skewed or the data do not seem to follow any particular shape or distribution (e. g. Normal) – Assumptions underlying parametric test not met – There are potentially influential outliers in the dataset – Sample size is small

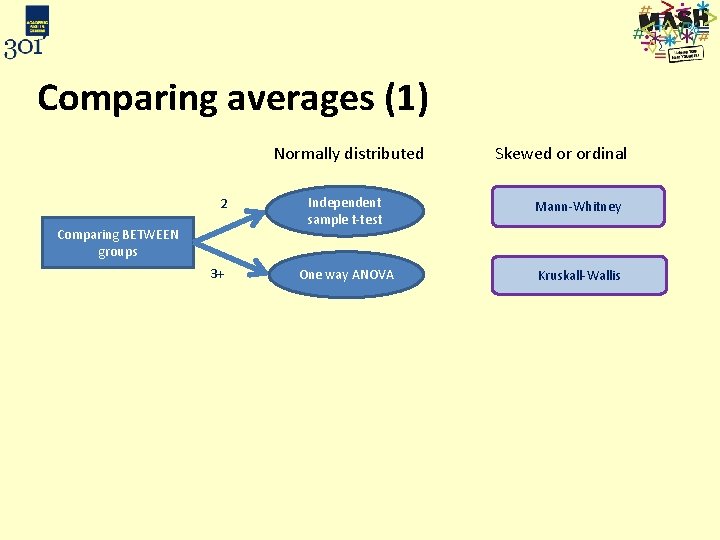
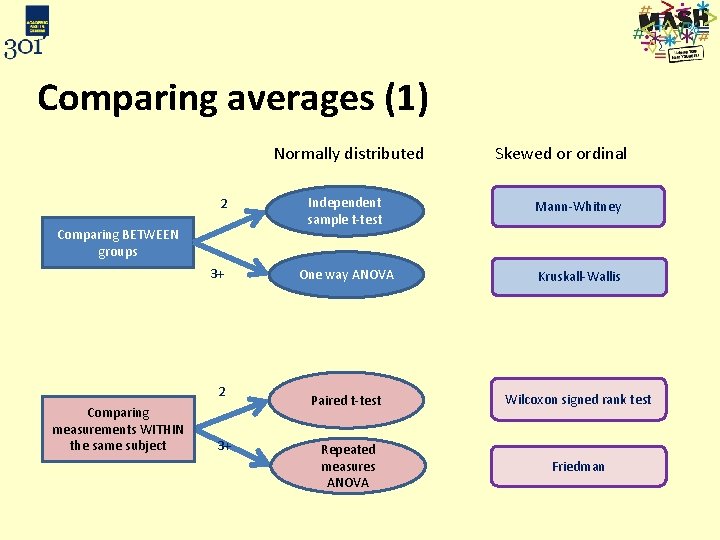
Comparing averages (1) Normally distributed 2 Comparing BETWEEN groups 3+ Skewed or ordinal Independent sample t-test Mann-Whitney One way ANOVA Kruskall-Wallis

Paired data (1) • Most commonly, measurements from the same individuals collected on more than one occasion • Can be used to look at differences in mean score: 2 or more time points e. g. before/after a diet 2 or more conditions e. g. hearing test at different frequencies Each person listened to a sound until they could no longer hear it at three different frequencies. Would use Repeated measures ANOVA to test for a difference between the frequencies.

Comparing averages (1) Normally distributed 2 Comparing BETWEEN groups 3+ 2 Comparing measurements WITHIN the same subject 3+ Skewed or ordinal Independent sample t-test Mann-Whitney One way ANOVA Kruskall-Wallis Paired t-test Wilcoxon signed rank test Repeated measures ANOVA Friedman

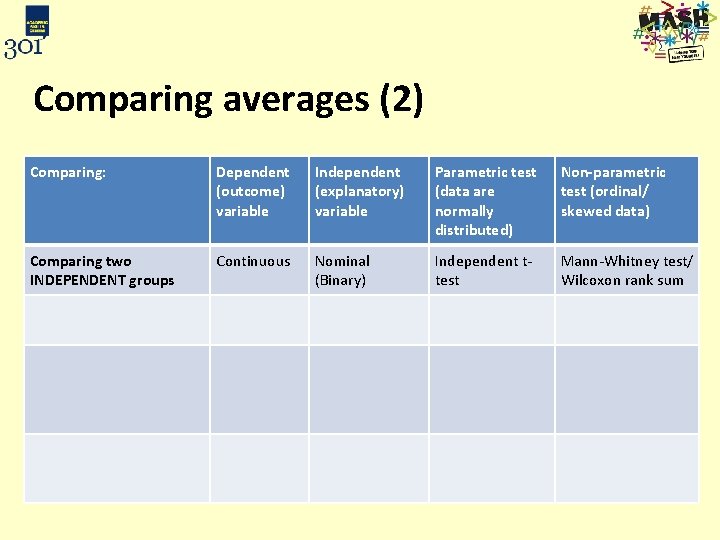
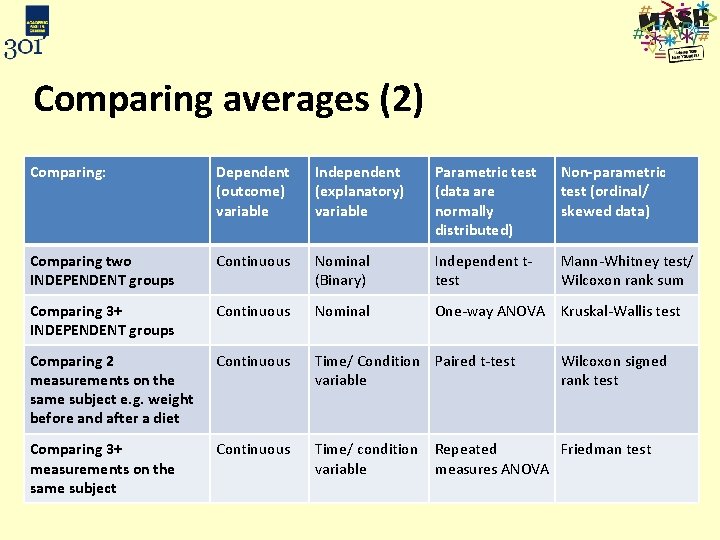
Comparing averages (2) Comparing: Dependent (outcome) variable Independent (explanatory) variable Parametric test (data are normally distributed) Non-parametric test (ordinal/ skewed data) Comparing two INDEPENDENT groups Continuous Nominal (Binary) Independent ttest Mann-Whitney test/ Wilcoxon rank sum Comparing 3+ INDEPENDENT groups Comparing 2 measurements on the same subject e. g. weight before and after a diet Comparing 3+ measurements on the same subject

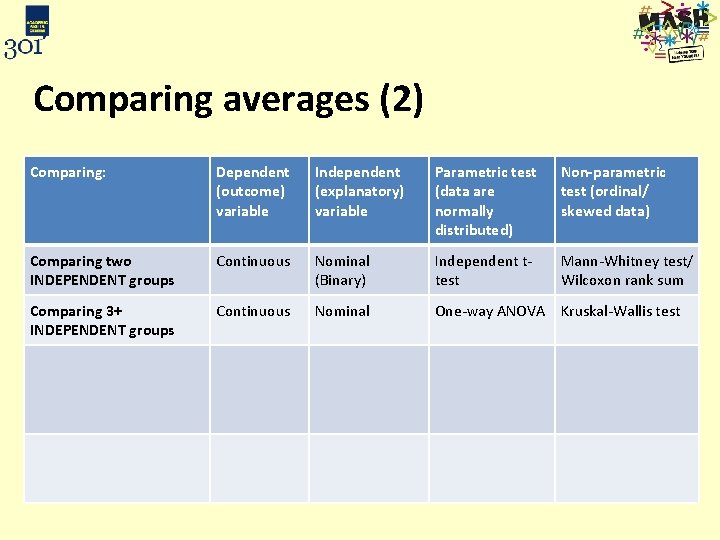
Comparing averages (2) Comparing: Dependent (outcome) variable Independent (explanatory) variable Parametric test (data are normally distributed) Non-parametric test (ordinal/ skewed data) Comparing two INDEPENDENT groups Continuous Nominal (Binary) Independent ttest Mann-Whitney test/ Wilcoxon rank sum Comparing 3+ INDEPENDENT groups Continuous Nominal One-way ANOVA Kruskal-Wallis test Comparing 2 measurements on the same subject e. g. weight before and after a diet Comparing 3+ measurements on the same subject

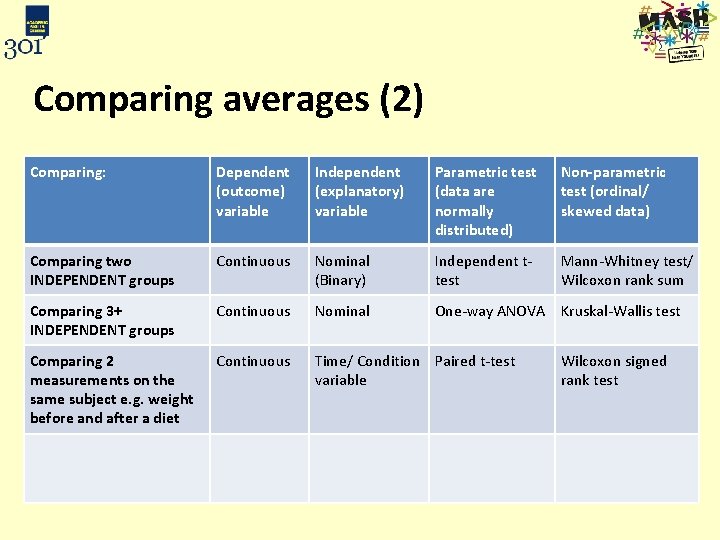
Comparing averages (2) Comparing: Dependent (outcome) variable Independent (explanatory) variable Parametric test (data are normally distributed) Non-parametric test (ordinal/ skewed data) Comparing two INDEPENDENT groups Continuous Nominal (Binary) Independent ttest Mann-Whitney test/ Wilcoxon rank sum Comparing 3+ INDEPENDENT groups Continuous Nominal One-way ANOVA Kruskal-Wallis test Comparing 2 measurements on the same subject e. g. weight before and after a diet Continuous Time/ Condition Paired t-test variable Comparing 3+ measurements on the same subject Wilcoxon signed rank test

Comparing averages (2) Comparing: Dependent (outcome) variable Independent (explanatory) variable Parametric test (data are normally distributed) Non-parametric test (ordinal/ skewed data) Comparing two INDEPENDENT groups Continuous Nominal (Binary) Independent ttest Mann-Whitney test/ Wilcoxon rank sum Comparing 3+ INDEPENDENT groups Continuous Nominal One-way ANOVA Kruskal-Wallis test Comparing 2 measurements on the same subject e. g. weight before and after a diet Continuous Time/ Condition Paired t-test variable Comparing 3+ measurements on the same subject Continuous Time/ condition variable Wilcoxon signed rank test Repeated Friedman test measures ANOVA

Examples?

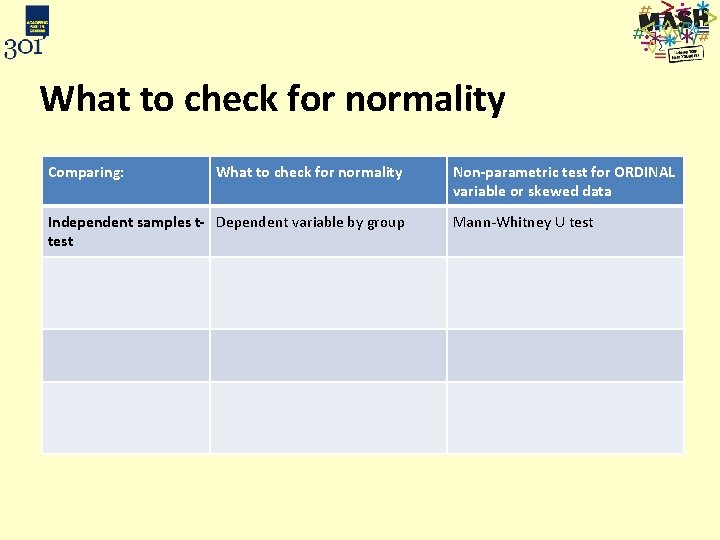
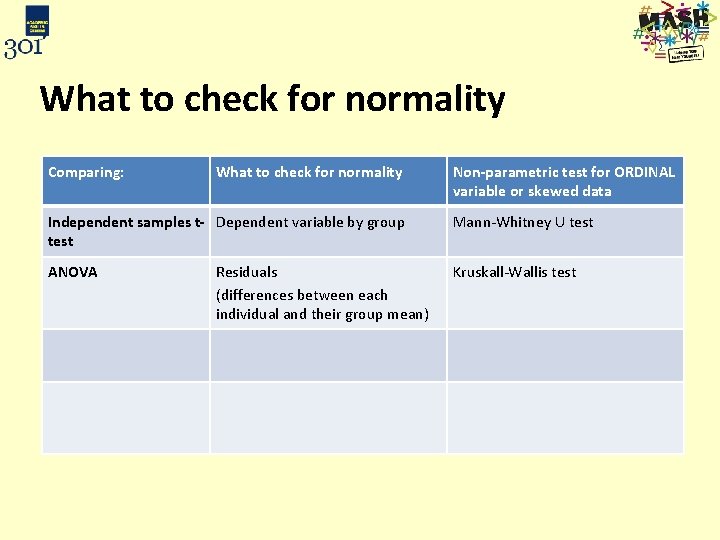
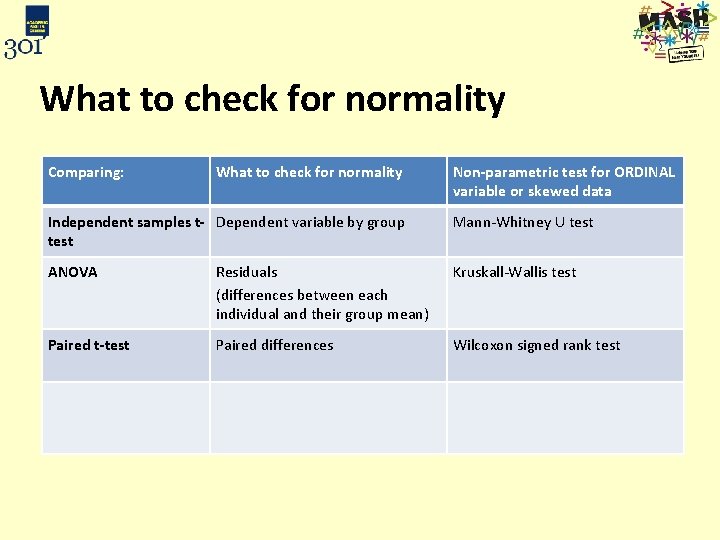
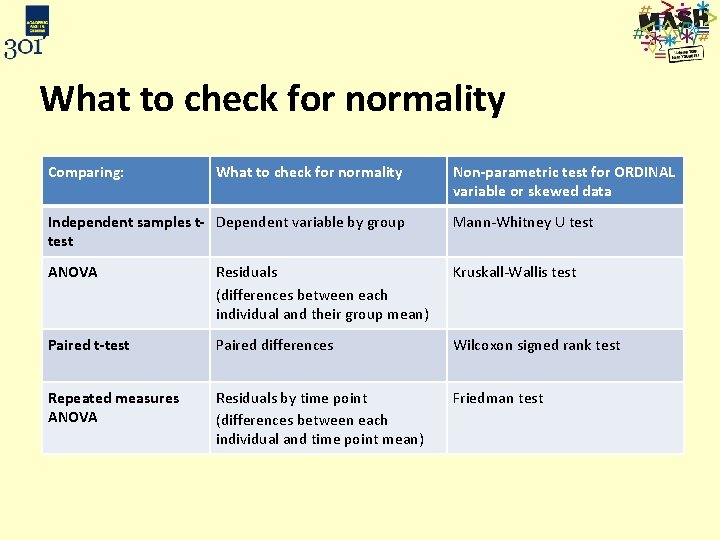
What to check for normality Comparing: What to check for normality Non-parametric test for ORDINAL variable or skewed data Independent samples t- Dependent variable by group test Mann-Whitney U test ANOVA Residuals (differences between each individual and their group mean) Kruskall-Wallis test Paired t-test Paired differences Wilcoxon signed rank test Repeated measures ANOVA Residuals by time point (differences between each individual and time point mean) Friedman test

What to check for normality Comparing: What to check for normality Non-parametric test for ORDINAL variable or skewed data Independent samples t- Dependent variable by group test Mann-Whitney U test ANOVA Residuals (differences between each individual and their group mean) Kruskall-Wallis test Paired t-test Paired differences Wilcoxon signed rank test Repeated measures ANOVA Residuals by time point (differences between each individual and time point mean) Friedman test

What to check for normality Comparing: What to check for normality Non-parametric test for ORDINAL variable or skewed data Independent samples t- Dependent variable by group test Mann-Whitney U test ANOVA Residuals (differences between each individual and their group mean) Kruskall-Wallis test Paired t-test Paired differences Wilcoxon signed rank test Repeated measures ANOVA Residuals by time point (differences between each individual and time point mean) Friedman test

What to check for normality Comparing: What to check for normality Non-parametric test for ORDINAL variable or skewed data Independent samples t- Dependent variable by group test Mann-Whitney U test ANOVA Residuals (differences between each individual and their group mean) Kruskall-Wallis test Paired t-test Paired differences Wilcoxon signed rank test Repeated measures ANOVA Residuals by time point (differences between each individual and time point mean) Friedman test

Example 1: Did gender affect ticket price paid on the Titanic? Steps: 1. 2. 3. 4. 5. What is the outcome variable? What is the grouping / explanatory variable? What methods are available to analyse these data? Check the assumptions Conduct the appropriate analysis and report the results What test do you think would be appropriate?

Example 1: Did gender affect ticket price paid on the Titanic? Steps: 1. What is the outcome variable? Ticket price 2. What is the grouping / explanatory variable? Gender 3. What methods are available to analyse these data? Comparing ticket price between two groups (male and female). Most appropriate method is independent samples t-test 4. Check the assumptions. Assumes that the groups are independent, the data in the two groups are normally distributed and the variability in the two groups is similar. 5. Conduct the appropriate analysis and report the results. If the assumptions for the t-test are not met, use the Mann-Whitney U test

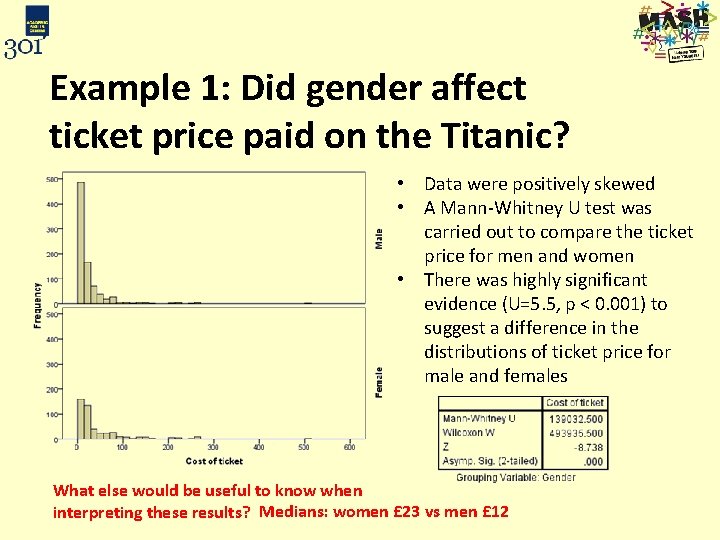
Example 1: Did gender affect ticket price paid on the Titanic? • Data were positively skewed • A Mann-Whitney U test was carried out to compare the ticket price for men and women • There was highly significant evidence (U=5. 5, p < 0. 001) to suggest a difference in the distributions of ticket price for male and females What else would be useful to know when interpreting these results? Medians: women £ 23 vs men £ 12

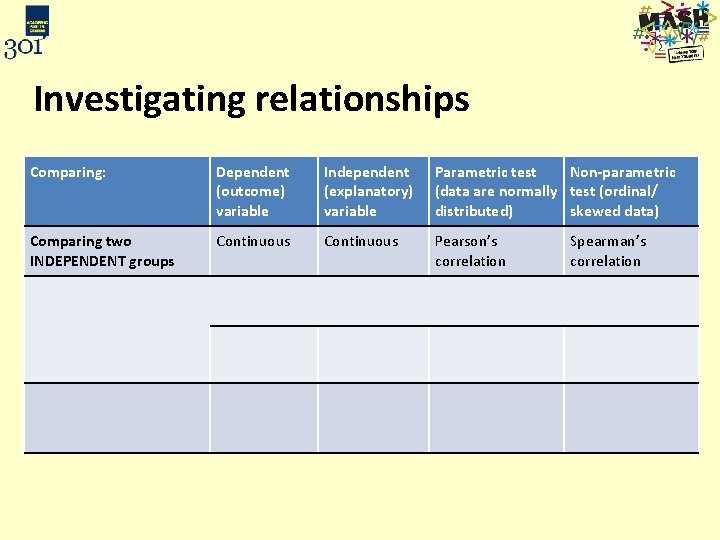
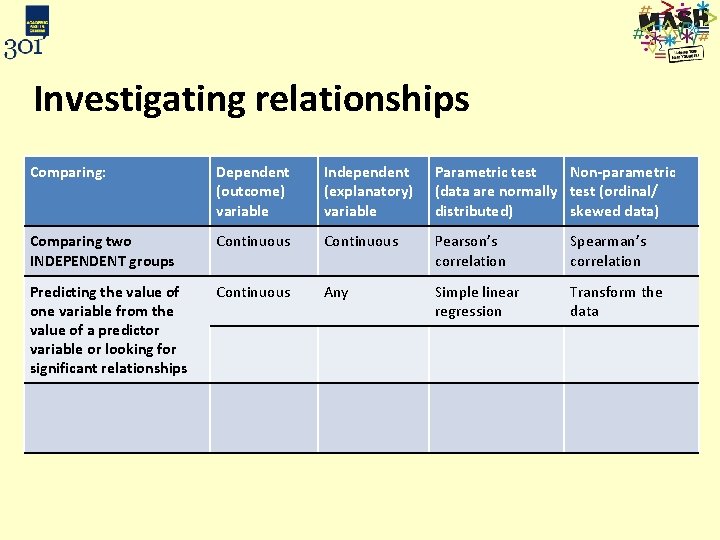
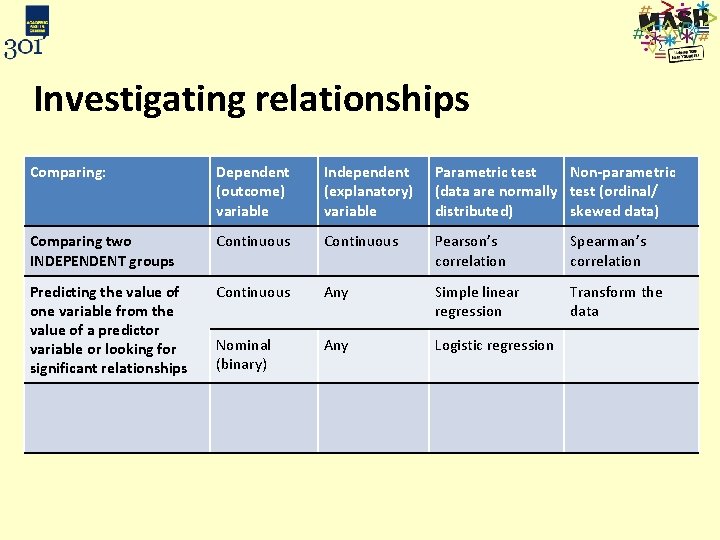
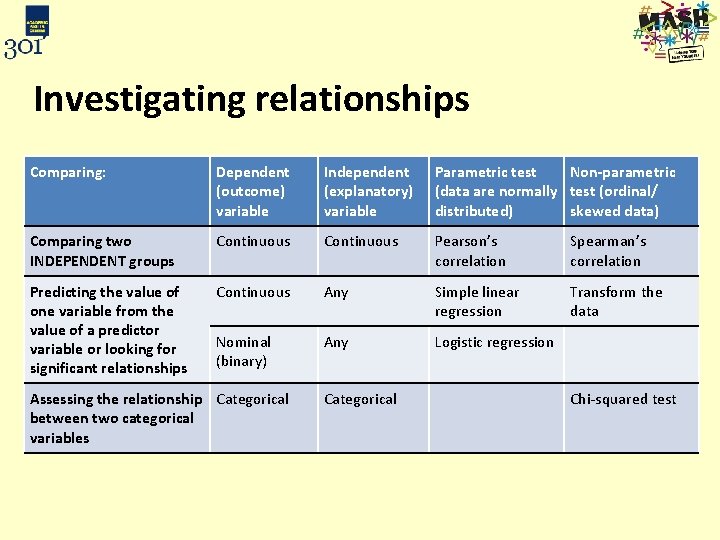
Investigating relationships Comparing: Dependent (outcome) variable Independent (explanatory) variable Parametric test Non-parametric (data are normally test (ordinal/ distributed) skewed data) Comparing two INDEPENDENT groups Continuous Pearson’s correlation Spearman’s correlation Predicting the value of one variable from the value of a predictor variable or looking for significant relationships Scale Any Simple linear regression Transform the data Nominal (binary) Any Logistic regression Assessing the relationship Categorical between two categorical variables Categorical Chi-squared test

Investigating relationships Comparing: Dependent (outcome) variable Independent (explanatory) variable Parametric test Non-parametric (data are normally test (ordinal/ distributed) skewed data) Comparing two INDEPENDENT groups Continuous Pearson’s correlation Spearman’s correlation Predicting the value of one variable from the value of a predictor variable or looking for significant relationships Continuous Any Simple linear regression Transform the data Nominal (binary) Any Logistic regression Assessing the relationship Categorical between two categorical variables Categorical Chi-squared test

Investigating relationships Comparing: Dependent (outcome) variable Independent (explanatory) variable Parametric test Non-parametric (data are normally test (ordinal/ distributed) skewed data) Comparing two INDEPENDENT groups Continuous Pearson’s correlation Spearman’s correlation Predicting the value of one variable from the value of a predictor variable or looking for significant relationships Continuous Any Simple linear regression Transform the data Nominal (binary) Any Logistic regression Assessing the relationship Categorical between two categorical variables Categorical Chi-squared test

Investigating relationships Comparing: Dependent (outcome) variable Independent (explanatory) variable Parametric test Non-parametric (data are normally test (ordinal/ distributed) skewed data) Comparing two INDEPENDENT groups Continuous Pearson’s correlation Spearman’s correlation Predicting the value of one variable from the value of a predictor variable or looking for significant relationships Continuous Any Simple linear regression Transform the data Nominal (binary) Any Logistic regression Assessing the relationship Categorical between two categorical variables Categorical Chi-squared test

Examples?

Example 2: two categorical variables Survival of the pushiest?

Example 2: Survival of the pushiest Research question: Was survival on the titanic linked to nationality? Dependent: Independent: Survival Nationality What test do you think you should use? Chi-squared test http: //www. independent. co. uk/news/world/australasia/more-britons-than-americans-died-on-titanic-because-they-queued-1452299. html

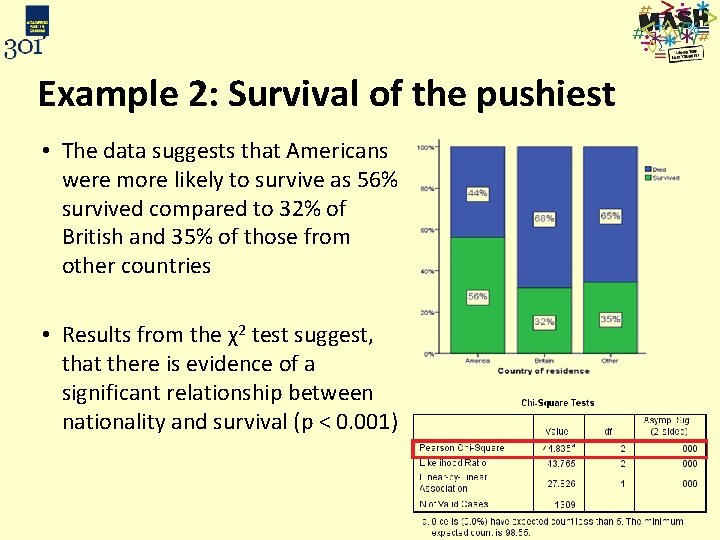
Example 2: Survival of the pushiest • The data suggests that Americans were more likely to survive as 56% survived compared to 32% of British and 35% of those from other countries • Results from the χ2 test suggest, that there is evidence of a significant relationship between nationality and survival (p < 0. 001)

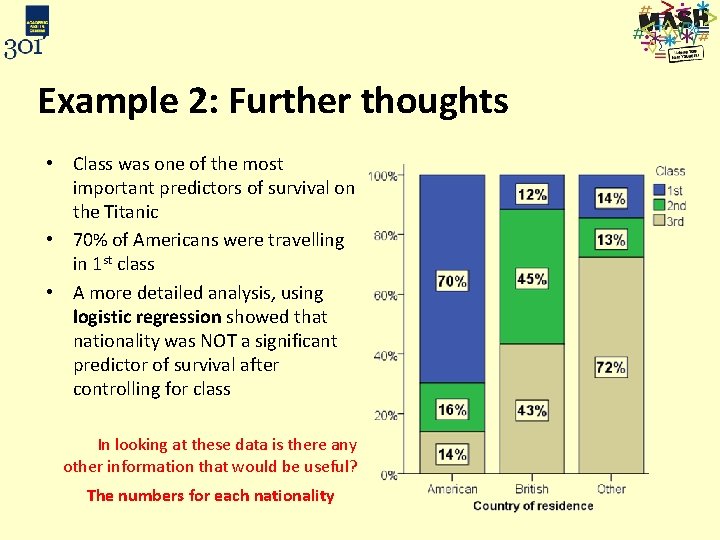
Example 2: Further thoughts • Class was one of the most important predictors of survival on the Titanic • 70% of Americans were travelling in 1 st class • A more detailed analysis, using logistic regression showed that nationality was NOT a significant predictor of survival after controlling for class In looking at these data is there any other information that would be useful? The numbers for each nationality

Learning outcomes • You should now know about: – Some useful approaches to analysing data • By the end of this session you should be able to: – Recognise different data types – Use a flowchart to decide which analysis method to use – Undertake some basic analyses and construct appropriate charts for your data

Exercises - Attempt the 4 exercises in SPSS - In each case you need to identify an appropriate analysis based on the dataset provided - Remember to check the assumptions for any analysis you conduct - Add value labels to the data if required - Use the flow charts & table to assist you

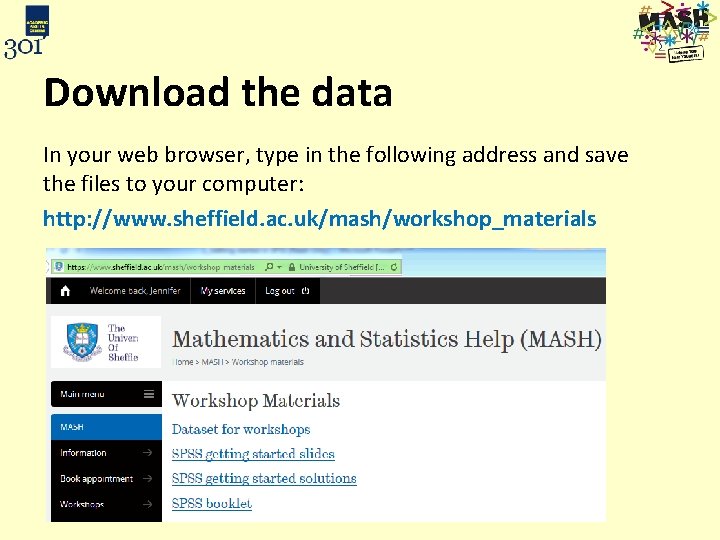
Download the data In your web browser, type in the following address and save the files to your computer: http: //www. sheffield. ac. uk/mash/workshop_materials

Maths And Statistics Help Statistics appointments: Mon-Fri (10 am-1 pm) Statistics drop-in: Mon-Fri (10 am-1 pm), Weds (4 -7 pm) http: //www. sheffield. ac. uk/mash

Resources: All resources are available in paper form at MASH or on the MASH website

Contacts Staff (stats) Jenny Freeman (j. v. freeman@sheffield. ac. uk) Basile Marquier (b. marquier@sheffield. ac. uk) Marta Emmett (m. emmett@sheffield. ac. uk) Website http: //www. sheffield. ac. uk/mash Follow MASH on twitter: @mash_uos