CHOOSING IN GROUPS MUNGER AND MUNGER Slides for

CHOOSING IN GROUPS MUNGER AND MUNGER Slides for Chapter 6 Two Dimensions: Elusive Equilibrium

Outline of Chapter 6 § Appropriations committee example § Equilibrium § Representing spatial preferences § Nonseparability and complementarity § Chaos and equilibria § Mathematical examples in multiple dimensions § Generalized Mean Voter Theorem (GMVT) Slides Produced by Jeremy Spater, Duke University. All rights reserved. 2

Appropriations committee example § Preferences over spending on two projects § Having two dimensions changes the problem: § Salience: How much importance does each person place on the two issues? § Separability: Ideal point in each dimension depends on decision on other dimension § Conditional ideal points § Multidimensional Amendments: Proposals can occur on multiple dimensions. Table 6. 1. Subcommittee ideal points on two projects Member Project 1 (millions of $) Project 2 (millions of $) Mr. A 150 120 (Median Project 2) Mr. B 50 40 Ms. C 100 70 Ms. D 10 200 Mr. E 80 (Median Project 1) 150 3

Equilibrium § Political equilibrium is a status quo position that cannot be defeated § The equilibrium position defeats any other alternative that can be proposed § Rules or institutions may prevent feasible alternatives that would defeat the equilibrium from being proposed § Equilibrium is rarely unique Slides Produced by Jeremy Spater, Duke University. All rights reserved. 5

Representing spatial preferences: utility functions § If proposals concern only one issue at a time, Mean Voter Theorem applies § Outcome is median of each issue § Indifference curves: Each point on an indifference curve is equally preferred § Separable preferences with equal salience: Circular indifference curves § Separable preferences with unequal salience: Elliptical indifference curves § Nonseparable preferences: Indifference curves could take many shapes! Slides Produced by Jeremy Spater, Duke University. All rights reserved. 6

Nonseparability: positive and negative complementarity § Negative complementarity: if we choose more of A, I want less of B § E. g. , Fixed budget: if we spend more on parks, I want to spend less on garbage collection § Positive complementarity: if we choose more of A, I want more of B § E. g. , every police officer should have a computer, so if we hire more officers, I want to buy more computers § Ideal point in each dimension is contingent on decision in the other dimension Slides Produced by Jeremy Spater, Duke University. All rights reserved. 10

Voting on complex proposals: definitions § Complex proposals: changes on more than one dimension § Germaneness rule: one dimension at a time § With germaneness rule and separable preferences, voting sequence does not matter § Pareto set: set of positions from which no one can be made better off without making someone else worse off § Condorcet winner: a position that beats or ties any other in pairwise contests § Example: median position with single-peaked preferences over one dimension § Win set (of z ): positions that will get more votes than z in pairwise contests § Formally: Slides Produced by Jeremy Spater, Duke University. All rights reserved. 14

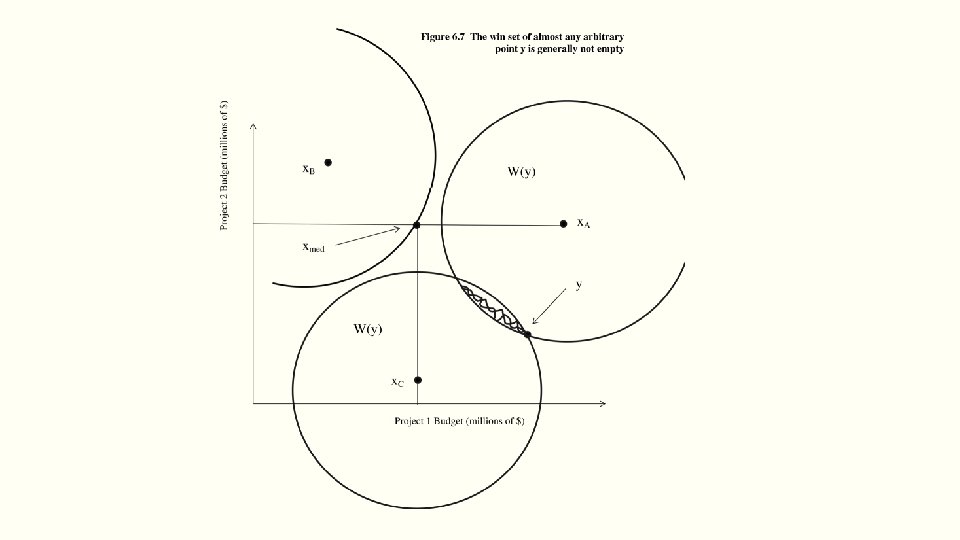
Chaos § Generally the win set of the median proposal (in >1 dimensions) is not empty! § Chaos result: for sincere voting, sequence of accepted proposals can go anywhere! § Outcome may not be in Pareto set § Majority rule can lead to an outcome that everyone agrees is bad! Slides Produced by Jeremy Spater, Duke University. All rights reserved. 16

Conditions for equilibrium § Plott conditions: ordinal pairwise symmetry § Sufficient but not necessary for unique equilibrium § Fairly restrictive § “Median in all directions”: § A line drawn through this point has at least half the voters on either side § Such a point is a Condorcet winner § This is a generalized version of the Median Voter Theorem Slides Produced by Jeremy Spater, Duke University. All rights reserved. 18

Multiple dimensions § Simple Euclidean distance (SED): § SED implies separability and equal salience § Weighted Euclidean distance (WED): § WED does not imply separability or equal salience Slides Produced by Jeremy Spater, Duke University. All rights reserved. 21

Multiple dimensions (2) § Ai is the matrix of salience and interaction terms (shown below for two dimensions) § Main diagonal elements are salience (weights) § We assume they are positive § Off-diagonal elements represent complementarity § We assume they are equal for simplicity (not required by theory) § Symmetry: If off-diagonal elements are 0 and main diagonal elements are 1 § Then WED reduces to SED § Indifference: Two points are indifferent if their WED from the ideal point is the same Slides Produced by Jeremy Spater, Duke University. All rights reserved. 23

Multiple dimensions (3) § We can write three general categories of indifference curves in matrix notation: § Ai = k I, where k is a constant: Circular indifference curves § Ai = s. I, where s is a vector of weights: Elliptical indifference curves; separable § Ai not diagonal: nonseparable preferences Slides Produced by Jeremy Spater, Duke University. All rights reserved. 24

Example: separable WED in two dimensions § Return to committee example. Consider Member B § B prefers y to z iff: § Let’s assume that AB looks like this: § Note that B’s preferences are separable, but the salience terms are not equal. Slides Produced by Jeremy Spater, Duke University. All rights reserved. 25

Example: separable WED in two dimensions (2) § Let’s go through the calculations: § In this example, B prefers y to z, because Slides Produced by Jeremy Spater, Duke University. All rights reserved. 26

Nonseparable preferences § Nonseparable preferences have an additional interaction term: § Positive a 12 indicates a negative complementarity (greater distance) § Negative a 12 indicates positive complementarity (lesser distance) Slides Produced by Jeremy Spater, Duke University. All rights reserved. 28

Nonseparable preferences (2) § Effects of the interaction term: § For positive complementarity: if issue j is fixed higher than the ideal point, then the conditionally ideal k value will be higher than the ideal point. § For negative complementarity: if issue j is fixed higher than the ideal point, then the conditionally ideal k value will be lower than the ideal point. § For positive or negative complementarity: if issue j is fixed at the ideal point, then the interaction term will be zero, and complementarity will have no effect. Slides Produced by Jeremy Spater, Duke University. All rights reserved. 29

Nonseparable preferences (3) § Calculating conditional preference: Say Project 1 budget is fixed at § We write out the WED: § Minimize the WED to find the Project 2 budget that maximizes the voter’s utility: § Note that the conditionally ideal Project 2 budget is not the same as the voter’s unconditionally ideal Project 2 budget. Slides Produced by Jeremy Spater, Duke University. All rights reserved. 30

Generalized Median Voter Theorem (GMVT) Assumptions: § N voters; k issues § Separable and symmetric preferences § “Separating hyperplane”: k-1 dimensions (e. g. , a line in 2 -space) that divides the ideal points of the voters into two separate groups. Theorem: An alternative y is the median if every hyperplane containing y has at least half the ideal points on either side of the hyperplane. Slides Produced by Jeremy Spater, Duke University. All rights reserved. 31