CHOOSING AN APPROPRIATE MODEL How to select a

CHOOSING AN APPROPRIATE MODEL How to select a theoretical model from an observed distribution (Click for the next slide)

MAKE A PICTURE AND DECIDE! Right now, your pictures will be Geometric figures- triangles or other simple shapes whose area you can calculate. Uniform: all observations are roughly equally likely. The picture will be roughly rectangular. Normal: the picture is roughly bell-shaped. The normal distribution is known informally as the “bell-curve. ” Let’s investigate uniform and Normal distributions just a little more. (Click for the next slide)

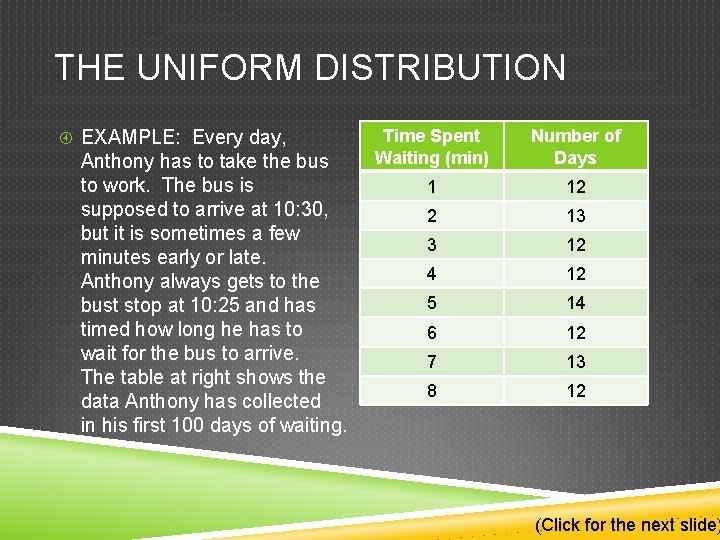
THE UNIFORM DISTRIBUTION EXAMPLE: Every day, Anthony has to take the bus to work. The bus is supposed to arrive at 10: 30, but it is sometimes a few minutes early or late. Anthony always gets to the bust stop at 10: 25 and has timed how long he has to wait for the bus to arrive. The table at right shows the data Anthony has collected in his first 100 days of waiting. Time Spent Waiting (min) Number of Days 1 12 2 13 3 12 4 12 5 14 6 12 7 13 8 12 (Click for the next slide)

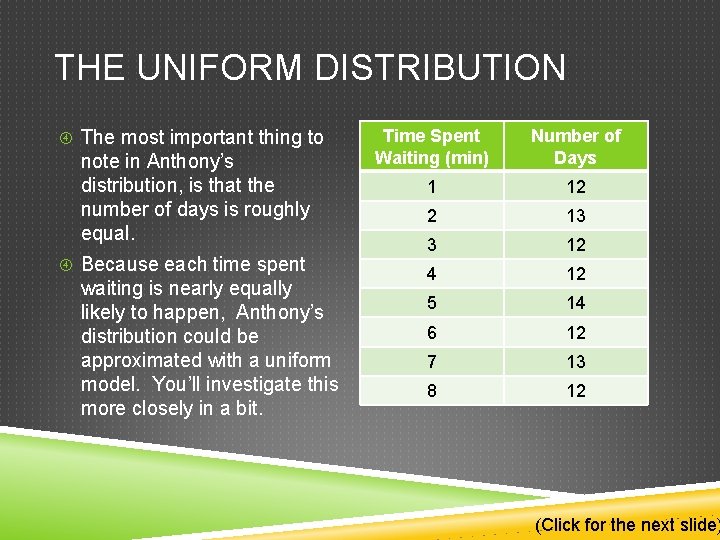
THE UNIFORM DISTRIBUTION The most important thing to note in Anthony’s distribution, is that the number of days is roughly equal. Because each time spent waiting is nearly equally likely to happen, Anthony’s distribution could be approximated with a uniform model. You’ll investigate this more closely in a bit. Time Spent Waiting (min) Number of Days 1 12 2 13 3 12 4 12 5 14 6 12 7 13 8 12 (Click for the next slide)

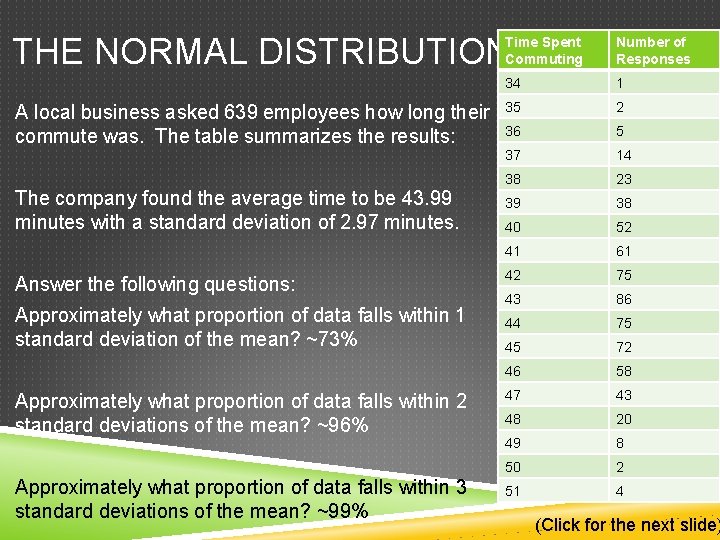
THE NORMAL DISTRIBUTION A local business asked 639 employees how long their commute was. The table summarizes the results: The company found the average time to be 43. 99 minutes with a standard deviation of 2. 97 minutes. Answer the following questions: Approximately what proportion of data falls within 1 standard deviation of the mean? Approximately what proportion of data falls within 2 standard deviations of the mean? Approximately what proportion of data falls within 3 standard deviations of the mean? Time Spent Commuting Number of Responses 34 1 35 2 36 5 37 14 38 23 39 38 40 52 41 61 42 75 43 86 44 75 45 72 46 58 47 43 48 20 49 8 50 2 51 4 (Click for the next slide)

THE NORMAL DISTRIBUTION A local business asked 639 employees how long their commute was. The table summarizes the results: The company found the average time to be 43. 99 minutes with a standard deviation of 2. 97 minutes. Answer the following questions: Approximately what proportion of data falls within 1 standard deviation of the mean? ~73% Approximately what proportion of data falls within 2 standard deviations of the mean? ~96% Approximately what proportion of data falls within 3 standard deviations of the mean? ~99% Time Spent Commuting Number of Responses 34 1 35 2 36 5 37 14 38 23 39 38 40 52 41 61 42 75 43 86 44 75 45 72 46 58 47 43 48 20 49 8 50 2 51 4 (Click for the next slide)

THE EMPIRICAL RULE The company’s data does not perfectly follow a normal distribution, but it is close. The rule we use to determine if data follows a roughly normal distribution is called The Empirical Rule or the 68 -95 -99. 7 rule. 68% of the observations/data falls within one standard deviation of the mean. 95% of the observations/data falls within two standard deviations of the mean 99. 7% of the observations/data falls within three standard deviations of the mean. (Click for the answer)

CHECK OUT THE VIDEO ON HOW TO APPLY THE EMPIRICAL RULE! HOLLA AT ME WITH WAYS TO MAKE THESE BETTER PEACE That’s all Folks!