CHNG 1 M HNH H THNG H thng











































![TÍNH e. At • Dùng Laplace ngược e. At=L-1[(s. I-A)-1] TÍNH e. At • Dùng Laplace ngược e. At=L-1[(s. I-A)-1]](https://slidetodoc.com/presentation_image/494955361beabd2646e22817df6e818d/image-48.jpg)

![Dùng MATLAB >> A=[-1 1; -1 -10]; >> b=[0; 10]; >> c=[1 0]; >> Dùng MATLAB >> A=[-1 1; -1 -10]; >> b=[0; 10]; >> c=[1 0]; >>](https://slidetodoc.com/presentation_image/494955361beabd2646e22817df6e818d/image-50.jpg)

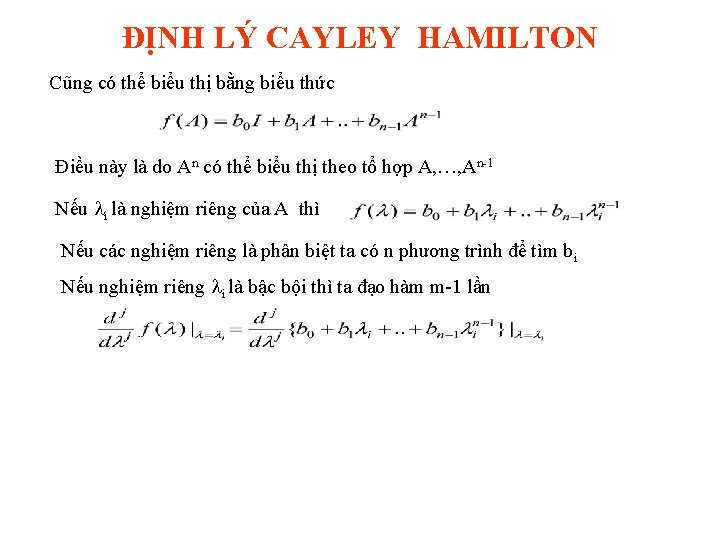
- Slides: 52

CHƯƠNG 1: MÔ HÌNH HỆ THỐNG • Hệ thống điều khiển bao gồm hệ thống được điều khiển (plant, process, controlled system), bộ điều khiển (controller) và các phần tử liên quan nhằm thực hiện một nhiệm vụ nào đó • Mô hình toán là biểu diễn toán học của hệ thống kỹ thuật, dùng để mô phỏng, phân tích và tổng hợp bộ điều khiển cho hệ thống u x y x: trạng thái trong của hệ thống, y: vectơ tín hiệu ra, u: vectơ tín hiệu vào

CHƯƠNG 1: MÔ HÌNH HỆ THỐNG Phân loại mô hình • Mô hìmh tuyến tính • Mô hình phi tuyến • Mô hình liên tục • Mô hình rờI rạc • Mô hình SISO • Mô hình MIMO

MÔ HÌNH TUYẾN TÍNH • Nếu yi là đáp ứng của tín hiệu vào ui thì đáp ứng của u = aiui là y = aiyi • Tinh chất xếp chồng cho phép khảo sát đáp ứng hệ thống với một vài tín hiệu đặc biệt như xung đơn vị, nấc đơn vị • Mô hình tuyến tính với một ngõ vào và một ngõ ra gọi là hệ SISO (single input-single output) • Nếu tín hiệu vào là liên tục ta có hệ tuyến tính liên tục • Nếu tín hiệu vào là rời rạc ta có hệ tuyến tính rời rạc

PHƯƠNG TRÌNH VI PH N • Hệ SISO liên tục mô tả bởi phương trình vi phân • Nếu hệ số ai bi là hằng số, hệ gọi là hệ tuyến tính bất biến • Nếu hệ số ai bi theo biến t thì ta có hệ tuyến tính không dừng, nếu chúng phụ thuộc các đối số khác ta gọi là hệ tuyến tính với thông số rải. • Tìm đáp ứng y theo u với phương trình vi phân có bậc n>2 là bài toán khó. • Chuyển mô hình sang dạng hàm truyền hay phương trình trạng thái.

HÀM TRUYỀN SISO 1/Biến đổi Laplace Cho tín hiệu x(t) thỏa mãn • x(t) =0 với t<0 • x(t) liên tục từng khúc Biến đổi Laplace của x(t) là Và biến đổi Laplace ngược của X(s) s = +jw, c >

HÀM TRUYỀN SISO 2/ Các định lý biến đổi Laplace • Tuyến tính Biến đổi của vi phân là với

HÀM TRUYỀN SISO • Biến đổi của tích phân là • Biến đổi của tích phân bội bậc n là • Biến đổi của hàm trễ • Biến đổi của là là • Biến đổi của tích chập • GiớI hạn cuối • Gía trị đầu x(t), t 0 là là là lim s. X(s), s 0 lim s. X(s), s

HÀM TRUYỀN SISO 3/ Bảng biến đổi Hàm thời gian Biến đổi Laplace Xung đơn vị (t) 1 Nấc đơn vị u 1(t) Dốc đơn vị t

HÀM TRUYỀN SISO 3/ Bảng biến đổi Hàm thời gian Biến đổi Laplace

HÀM TRUYỀN SISO 3/ Bảng biến đổi Hàm thời gian sin at Biến đổi Laplace

HÀM TRUYỀN SISO 3/ Bảng biến đổi Hàm thời gian cos at 1 - cos at Biến đổi Laplace

HÀM TRUYỀN SISO 4/ Hàm truyền hệ SISO • Cho hệ thống mô tả bởi phương trình vi phân Lấy biến đổi Laplace hai vế với giả sử điều kiện đầu bằng 0 Hàm truyền hệ thống là • Hàm truyền là hàm theo biến phức s, là phân số thực- hữu tỷ • Hàm truyền là hợp thức (proper) nếu m n và hợp thức chặt (strictly proper) nếu m<n , r=n-m gọi là bậc tương đối của hệ • Hàm truyền là bền nếu nghiệm của đa thức mẫu số có phần thực âm • Hàm truyền thực- hữu tỷ, hợp thức chặt, bền là pha cực tiểu nếu các nghiệm của tử số có phần thực âm

HÀM TRUYỀN SISO 5/ Đáp ứng • Hàm trọng lượng g(t) là đáp ứng y(t) khi tín hiệu vào là hàm xung đơn vị (t), là biến đổi Laplace ngược của hàm truyền G(s) • Hàm quá độ h(t) là đáp ứng y(t) khi tín hiệu vào là hàm nấc đơn vị 1(t), là biến đổi Laplace ngược của hàm truyền H(s) = G(s)/s • Muốn tìm biến đổi Laplace ngược của phân số hữu tỷ H(s) theo s ta phân tích thành các hàm phân thức tối giản A, Aki, Bk, Ck là hằng số, ak là cực thực (nghiệm mẫu số) bậc bội rk, k ±j k là cực phức. • Tra bảng để tìm các hàm thời gian tương ứng

HÀM TRUYỀN SISO • Trường hợp nghiệm đơn pi Các số ri gọi là thặng dư • Trường hợp nghiệm bội, thực p 1 bậc q • Dùng MATLAB [r, p, k]=residue([1], [1 1. 5 1]) r= p= 0 - 0. 7559 i -0. 7500 + 0. 6614 i 0 + 0. 7559 i -0. 7500 - 0. 6614 i k= []

HÀM TRUYỀN SISO 5/ Đáp ứng Dùng các biến đổi sau: Ví dụ: cho hàm truyền Ta tính được:

HÀM TRUYỀN SISO • Đáp ứng xung có dạng • Có thể dùng Matlab để vẽ đáp ứng ts=[3]; ms=[1 2 5 0]; ht=tf(ts, ms); y=impulse(ht); z=step(ht); hold on plot(y) plot(z) • Dùng công cụ Symbolic Math Toolbox để tìm biểu thức toán học >>syms t s; >> ht=3/(s^3+2*s^2+5*s); >> g=simplify(ilaplace(ht, t)) g = 3/5 -3/5*exp(-t)*cos(2*t)-3/10*exp(-t)*sin(2*t)

HÀM TRUYỀN MIMO • Với hệ có p đầu vào và q đầu ra, hàm truyền giữa ngõ vào thứ i và ngõ ra thứ j là • Dùng ký hiệu vectơ ta có • G(s) là ma trận hàm truyền q hàng p cột

PHƯƠNG TRÌNH TRẠNG THÁI • Hệ thống được biểu thị bởi đáp ứng ra y theo tín hiệu vào u, đáp ứng ra là những tín hiệu đo được, ngoài ra còn những trạng thái bên trong x của hệ thống thay đổi theo tín hiệu vào, x là vectơ trạng thái có thể có một vài thành phần không đo được, hoặc có một vài thành phần trùng với một vài thành phần của vectơ ngõ ra y • Với hệ có n biến trạng thái, p ngõ vào và q ngõ ra, ta có phương trình trạng thái A: ma trận n*n, B: ma trận n*p, C: ma trận q*n, D: ma trận q*p • Các ma trận gồm các số hạng thực, có thể là hằng số, thay đổi theo thời gian hay theo một đối số

PHƯƠNG TRÌNH TRẠNGTHÁi • Thành lập phương trình trạng thái từ hàm truyền • Có nhiều phương pháp thành lập pttt • Dạng companion thứ nhất (dạng chính tắc điều khiển) Cho hệ SISO có hàm truyền bậc n Gọi A(s) đa thức mẫu số, Y(s) viết lại là Đặt các biến trạng thái như sau:

PHƯƠNG TRÌNH TRẠNGTHÁi

PHƯƠNG TRÌNH TRẠNGTHÁI • Viết lại dưới dạng pttt, ta được các ma trận x là vectơ n chiều, u và y là vô hướng Các hệ số của đa thức mẫu số được đảo dấu và xuất hiện ở hàng cuối của A, C chứa các hệ số của tử số

PHƯƠNG TRÌNH TRẠNGTHÁI • Ví dụ: Cho hàm truyền Ta được pttt

PHƯƠNG TRÌNH TRẠNGTHÁI • Dạng companion thứ hai (dạng chính tắc quan sát)

PHƯƠNG TRÌNH TRẠNG THÁI • Dạng chính tắc Jordan Phân tích hàm truyền thành tổng các phân số theo các nghiệm của đa thức mẫu số. Gỉa sử các nghiệm là đơn Đặt các biến trạng thái như sau:

PHƯƠNG TRÌNH TRẠNG THÁI • Dạng chính tắc Jordan Trường hợp G(s) có m cực bội phân biệt 1, 2, , … m với độ bội n 1, n 2, …, nm; n = n 1+ n 2+ …+nm, phân tích thành phân số riêng

PHƯƠNG TRÌNH TRẠNG THÁI • Với mỗi Hi liên kết phương trình trạng thái bậc ni i là ma trận có dạng Jordan

PHƯƠNG TRÌNH TRẠNG THÁI • kết hợp m nghiệm ta có phương trình trạng thái là ma trận chéo khối, các ma trận con trên đường chéo thuộc dạng Jordan

PHƯƠNG TRÌNH TRẠNG THÁI • Trường hợp nghiệm phức: giả sử có ba cực là s = + j , s = - j và s = Khai triển phân số riêng phần Dùng phép đổi biến

PHƯƠNG TRÌNH TRẠNG THÁI Phương trình trạng thái mới là:

PHƯƠNG TRÌNH TRẠNG THÁI • Với một đối tượng, có thể có nhiều phương trình trạng thái khác nhau • Ví dụ: Dạng điều khiển Dạng quan sát Dạng chính tắc

PHƯƠNG TRÌNH TRẠNG THÁI Transfer function: s+3 -----------s^3 + 9 s^2 + 24 s + 20 • Dùng MATLAB ht=tf([1 3], [1 9 24 20]) Pttt=ss(ht) a= x 1 x 2 x 3 c= x 1 -9 x 2 16 0 0 y 1 x 3 0 8 0 d= b= u 1 x 1 0. 25 x 2 0 x 3 0 -1. 5 -0. 1563 x 1 0 x 2 x 3 0. 25 0. 09375 u 1 y 1 0 Continuous-time model.

PHƯƠNG TRÌNH TRẠNG THÁI Pttt=canon(ht, ’companion’) a= x 1 x 2 x 3 x 1 0 0 -20 x 2 1 0 -24 x 3 0 1 -9 b= u 1 c= y 1 0 1 -6 d= y 1 0 x 2 0 x 3 0 Transfer function: s+3 ----------s^3 + 3 s^2 + 3 s + 2 pttt=canon(ht, 'modal') u 1 Continuous-time model. x 1 1 ht=tf([1 3], conv([1 2], [1 1 1])) x 1 x 2 x 3

PHƯƠNG TRÌNH TRẠNG THÁI a= c= x 1 x 2 x 1 -2 0 x 2 0 -0. 5 x 3 0 -0. 866 b= x 3 0 x 1 x 2 y 1 -0. 1443 0. 5455 0. 866 -0. 5 d= u 1 x 1 -2. 309 u 1 y 1 0 x 2 -1. 528 x 3 2. 646 Continuous-time model. x 3 0. 189

ĐỔI PTTT RA HÀM TRUYỀN Cho phương trình trạng thái Lấy biến đổi Laplace hai vế Trường hợp xo = 0, ta viết G(s) là ma trận hàm truyền bậc ny * nu Nếu y và u là vô hướng G(s) là phân số hữu tỷ

MỘT SỐ CÔNG THỨC ĐẠI SỐ MA TRẬN • Ma trận A m hàng n cột là một tập hợp các phần tử aij xếp thành bảng m hàng và n cột: Amxn = (aij), i = 1, 2, …, m; j =1, 2, . . , n • Cộng trừ hai ma trận cùng số hàng, số cột: C = A+B = (cij) = (aij bij) • Kết quả nhân ma trận A với số vô hướng x là ma trận cùng kích thước B = Ax = x. A= (xaij) • Nhân hai ma trận Amxp và Bpxn là ma trận Cmxn số cột của A phải bằng số hàng của B • Chuyển vị của ma trận Amxn là Bnxm= AT, bij= aji • Ma trận chéo là ma trận vuông với aij= 0 khi i j • Ma trận đơn vị là ma trận chéo I với aii=1 • Hạng của ma trận là số các vectơ hàng độc lập tuyến tính hay số các vectơ cột độc lập tuyến tính

MỘT SỐ CÔNG THỨC ĐẠI SỐ MA TRẬN ĐỊNH THỨC • Định thức ma trận vuông Anxn là số thực hay phức • (Aij) là ma trận có được từ ma trận A bằng cách bỏ hàng i cột j • Biểu thức (-1)i+jdet(Aij) gọI là đồng thừa của phần tử aij • Ma trận vuông bậc 2 có định thức là a 11 a 22 -a 12 a 21 • Ma trận có định thức bằng 0 là ma trận suy biến (singular), có hai hàng hay hai cột phụ thuộc tuyến tính (giống nhau) det(A)=det(AT), det(AB)=det(A)det(B), det( A)= ndet(A) • Ma trận adjoint của ma trận vuông A là ma trận chuyển vị của ma trận có được bằng cách thay mỗi phần tử cúa A bằng đồng thừa của phần tử đó • Ma trận đảo của ma trận A vuông không bất thường là

MỘT SỐ CÔNG THỨC ĐẠI SỐ MA TRẬN Ví dụ A= A=[3 -1; 0 1; 2 0] 3 -1 B=[1 0 -1; 2 1 0] 0 1 2 0 C=A*B D=B*A det(A) B= C= 1 0 -1 1 -1 -3 2 1 0 2 0 -2 D= ? ? ? Error using ==> det Matrix must be square. E=det(D) ans = inv(D) -0. 2000 D^-1 -1. 2000 0. 2000 1 -1 6 -1 E= 5

ĐỊNH LÝ CAYLEY HAMILTON Ma trận A có phương trình đặc trưng là

MỘT SỐ CÔNG THỨC ĐẠI SỐ MA TRẬN • AA-1=A-1 A=I, I là ma trận vuông chéo đơn vị • (AB)-1=B-1 A-1 • Vết ma trận vuông là tổng các số hạng đường chéo • tr(A*B)=tr(B*A) • tr(S-1 AS)=tr(A), S là ma trận vuông không suy biến bất kỳ • Chuẩn ma trận: độ đo kích thức của ma trận • Chuẩn Frobenius (chuẩn Euclide): • Chuẩn bậc 1: tổng lớn nhất trong số các tổng của các module các số hạng cùng một cot • Chuẩn bậc 2: giá trị riêng lớn nhất của ATA • Chuẩn vô cùng: tổng lớn nhất trong số các tổng của các module các số hạng cùng một hang

MỘT SỐ TÍNH CHẤT QUAN TRỌNG (s. I-A)+ là ma trận adjoint của A Định thức |s. I-A| chính là mẫu số hàm truyền, gọi là đa thức đặc trưng Nghiệm của đa thức định thức | I-A| là trị riêng của ma trận A, cũng chính là nghiệm cỉa mẫu số hàm truyền Ví dụ: Đa thức đặc trưng: Hàm truyền:

ĐỔI PTTT RA HÀM TRUYỀN Ví dụ: Pttt = ss ([-0. 01 0; 0 -0. 02], [1 1; -0. 004 0. 002], [0. 01 0; 0 1], 0) a= c= x 1 -0. 01 x 2 0 -0. 02 b= x 1 x 2 y 1 0. 01 0 y 2 1 0 d= u 1 fromu 2 input 1 to output. . . Transfer function 1 1 0. 01 x 1 u 2 function from input 2 to output. . . Transfer y 1 00. 01 0 x 2 -0. 004 #1: ---- y 2 0 #1: 0 ---- s + 0. 01 Ht = tf(pttt) -0. 004 0. 002. s + 0. 01 0. 002 #2: -------- s + 0. 02

ĐỔI PTTT RA HÀM TRUYỀN Ví dụ: >> A=[0 1 0; 0 -1 1; 0 -1 -10] >>B=[0 0 10]' A= B= 0 1 0 0 0 -1 1 0 0 -1 -10 C= D= 1 0 10 >> C=[1 0 0] >> D=0 E= >> E = poly (A) 1. 0000 11. 0000 0 >>sys = ss(A, B, C, D); >>ht = tf(sys) >> nghiem=roots(E) Transfer function: 10 nghiem = 0 ---------- -9. 8875 s^3 + 11 s^2 + 11 s -1. 1125 0 0

TRỊ RIÊNG • Trị riêng (eigenvalue) của ma trận vuông A là nghiệm của phương trình đặc trưng |s. I-A| • Nếu 1, 2, … n là các trị riêng của A thì tr(A)= • Nếu 1, 2, … n là các trị riêng của A thì cũng là trị riêng của AT • Nếu 1, 2, … n là các trị riêng của A thì 1/ i là trị riêng của A-1 >>A = [0 1 0; 0 0 1; -2 -1 -5] d= A= >> d = eig(A) 0 1 0 -4. 8791 >> e = eig (A') 0 0 1 -0. 0605 + 0. 6374 i -2 -1 -5 -0. 0605 - 0. 6374 i >> f= eig(inv(A)) e= f= -0. 0605 + 0. 6374 i -0. 1475 + 1. 5549 i -0. 0605 - 0. 6374 i -0. 1475 - 1. 5549 i -4. 8791 -0. 2050

VECTƠ RIÊNG • Vectơ riêng (eigenvector) vi của ma trận A liên kết với nghiệm riêng i là nghiệm của phương trình ( i I-A) vi = 0 • Ví dụ: Phương trình đặc trưng: | I-A|= 2 -1 1 = 1, 2 = -1 Nghiệm riêng: Vectơ riêng v 1 với 1 là nghiệm của phương trình v 12 = 0, v 11 bất kỳ, chọn bằng 1 Tương tự vectơ riêng thứ hai thỏa phương trình -2 v 21+v 22 = 0, chọn tùy ý v 21=1, suy ra v 22 = 2 Các vecơ riêng là [v, d] = eig(A) v= d= 1. 0000 0. 4472 1 0 0 0. 8944 0 -1

VECTƠ RIÊNG TRỊ BỘI Trường hợp 1 là nghiệm bội bậc m Có m vectơ riêng tương ứng giải bởi các phương trình Ví dụ: Các trị riêng là 1 = -5, 2 = 3 = -2 Vectơ riêng ứng với trị riêng 1 = -5 là v 1= [0 0 1]T Giải phương trình Được vectơ riêng v 2 = [1 0 0]T Giải phương trình Được vectơ riêng v 3 = [1 1 0]T

NGHIỆM CỦA PTTT dx/dt=Ax+Bu Hàm mũ ma trận e. At: e. A 0=I, e. Ate-At=I, e. Aue. Av=e. A(u+v) Biến đổi Laplace của e. At là (s. I-A)-1

NGHIỆM CỦA PTTT dx/dt=Ax+Bu Xét phương trình dx/dt=Ax+Bu Nhân hai vế với e-At và chuyển vế Dùng tính chất đạo hàm Lấy tích phân hai vế Ta được kết quả
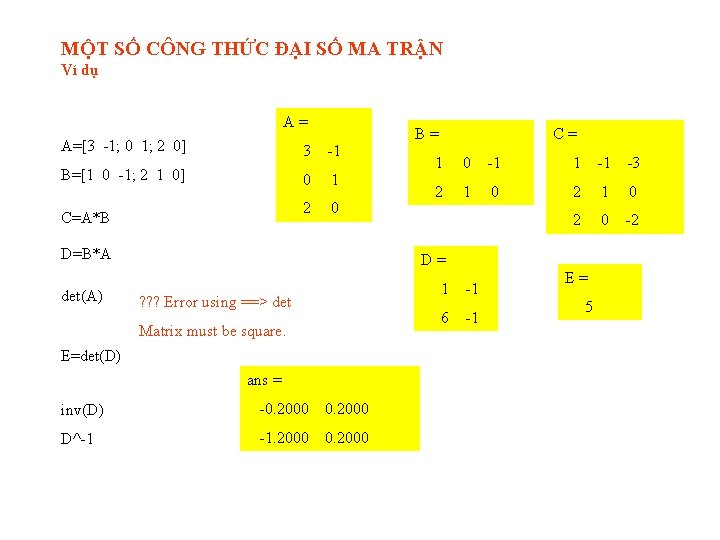
![TÍNH e At Dùng Laplace ngược e AtL1s IA1 TÍNH e. At • Dùng Laplace ngược e. At=L-1[(s. I-A)-1]](https://slidetodoc.com/presentation_image/494955361beabd2646e22817df6e818d/image-48.jpg)
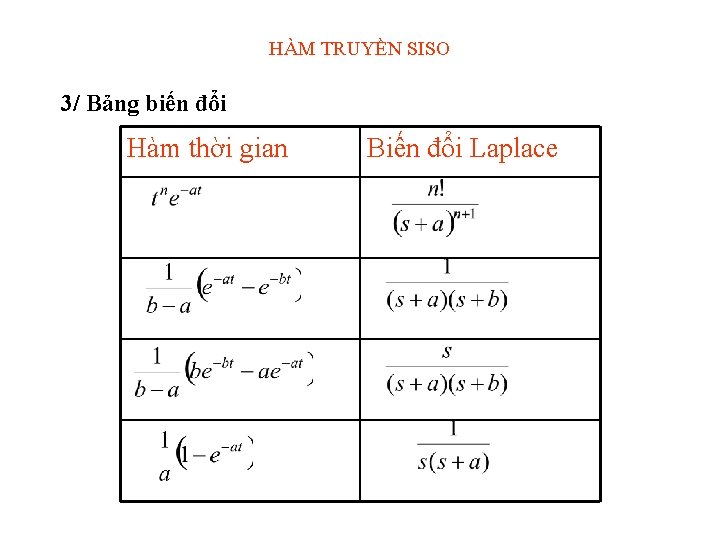
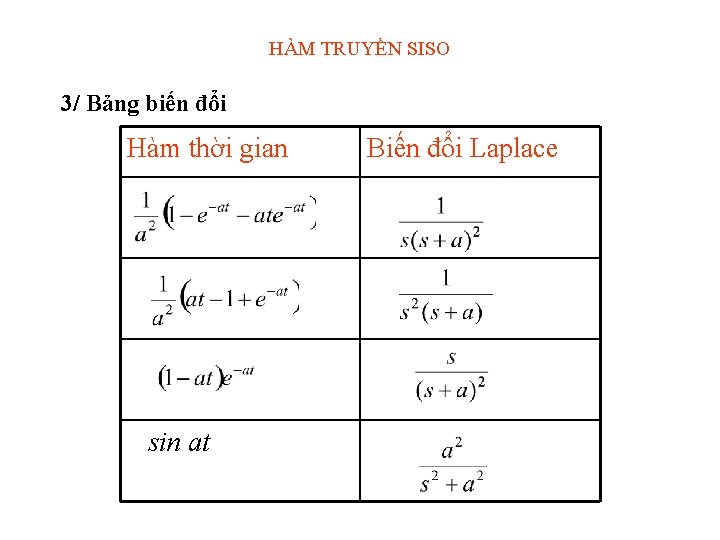
TÍNH e. At • Dùng Laplace ngược e. At=L-1[(s. I-A)-1]

![Dùng MATLAB A1 1 1 10 b0 10 c1 0 Dùng MATLAB >> A=[-1 1; -1 -10]; >> b=[0; 10]; >> c=[1 0]; >>](https://slidetodoc.com/presentation_image/494955361beabd2646e22817df6e818d/image-50.jpg)
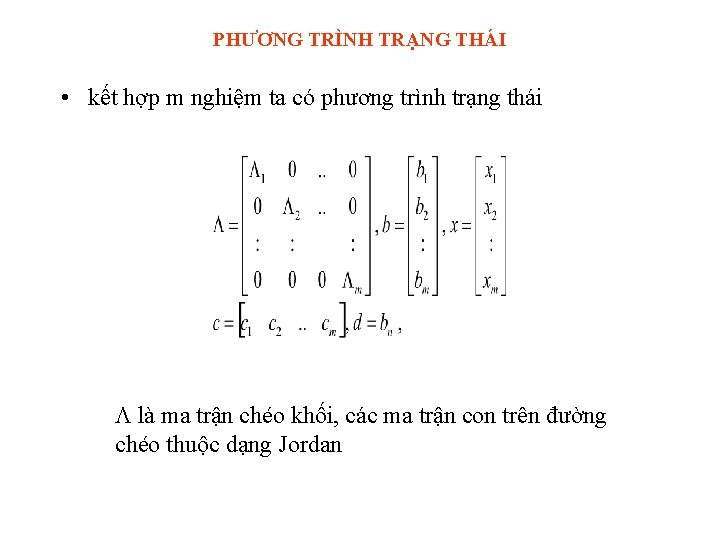
Dùng MATLAB >> A=[-1 1; -1 -10]; >> b=[0; 10]; >> c=[1 0]; >> model=ss(A, b, c, 0); >> [y, t, X]=step(model); >> plot(y) >> plot(X)

ĐỊNH LÝ CAYLEY HAMILTON Ma trận A có phương trình đặc trưng Thay bằng A ta có phương trình Thật vậy, từ hai đẳng thức trên ta có Vì Nên vế phải chia hết cho I-A, vậy vế trái cũng chia hết cho I-A, vậy p( )I chia hết cho I-A và p(A) cũng vậy p(A) không chứa mà chia hết cho I-A vậy p(A) = 0 ĐL C-H: hàm f(A) theo ma trận A biểu thị bằng chuỗi
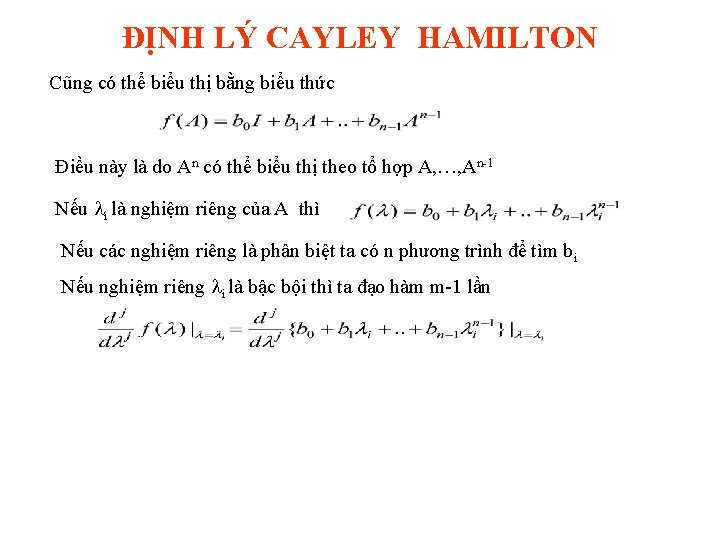
ĐỊNH LÝ CAYLEY HAMILTON Cũng có thể biểu thị bằng biểu thức Điều này là do An có thể biểu thị theo tổ hợp A, …, An-1 Nếu i là nghiệm riêng của A thì Nếu các nghiệm riêng là phân biệt ta có n phương trình để tìm bi Nếu nghiệm riêng i là bậc bội thì ta đạo hàm m-1 lần