CHME 420 Mass Transfer 2 b Differential Equations

CHME 420: Mass Transfer 2 b. Differential Equations for Steady-State Molecular Diffusion

One-Dimensional (1 D) Mass Transfer n Consider a binary mixture of A and B n There are two common cases to consider for molecular diffusion: 1. Diffusion of A through stagnant B (v. B = 0) (unimolecular diffusion, UMD) UMD NB = 0 2. Equimolar Counter Diffusion (EMCD) EMCD NB = – NA 2

Example 1: Arnold Cell (UMD) n used to measure diffusion coefficients (DAB) of gases. n It consist of a narrow tube which is partly filled with pure liquid “A”, and is maintained at a constant temperature and pressure. n Gas “B” flows across the open end of the cell and has negligible solubility in the liquid. Develop an expression for the mass transfer of vaporizing A n 3

Solution Assumptions: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. B is insoluble in A A is volatile and exerts a vapor pressure Gas inside tube is still Liquid level inside tube is constant z 1 is constant No reaction RA = 0 1 D flux along z Uniform cross sectional area Constant T and PT in gas within the tube Steady state Evaporation of A is limited by the diffusion of A 4

Solution (Continued) n Differential equation of mass transfer: – NA + RA = ∂c. A/∂t Similarly, for component B: d. NBz/dz = 0 Since B is insoluble in A NB|z 1 = 0 Flux of B is zero throughout the diffusion path (Steady State) Component B is a stagnant gas NB = 0 5

Solution (Continued) Flux Equation If the gas flow is high A is swept away y. A 2 ~ 0 (very small) Boundary Conditions: 1: y. A= y. A 1=x. A. PA*/PT @ z=z 1 2: y. A= y. A 2 @ z = z 2 6

Solution (Continued) n n Recall that (y. A + y. B = 1) y. B changes with z The logarithmic-mean average concentration of component B is defined as: Therefore: 7

Solution (Continued) n Concentration Profiles: BC 1: BC 2: Integration Solving for C 2 from both equations and subtracting: Separation of var. s Integration 8

Substituting Constants 9

Example 2: Equimolar Counter Diffusion (EMCD) n Assumptions: 1. 2. 3. 4. 5. 6. 7. NB z 2 Steady state (constant flux) Uniform Cross sectional area NA 1 D flux (along z) Constant T and PT constant c. T No gas phase chemical reaction RA = 0 Binary mixture of A and B DAB is constant z 1 10

Solution (Continued) n Differential equation of mass transfer: – NA + RA = ∂c. A/∂t Similarly, for component B: d. NBz/dz = 0 Since EMCD NB = - NA 11

Solution (Continued) Flux Equation Boundary Conditions: 1: y. A= y. A 1 @ z=z 1 2: y. A= y. A 2 @ z = z 2 12

Solution (Continued) n Concentration Profiles: BC 1: BC 2: Integration Solving for C 2 from both equations: Separation of var. s Integration 13

Substituting Constants 14

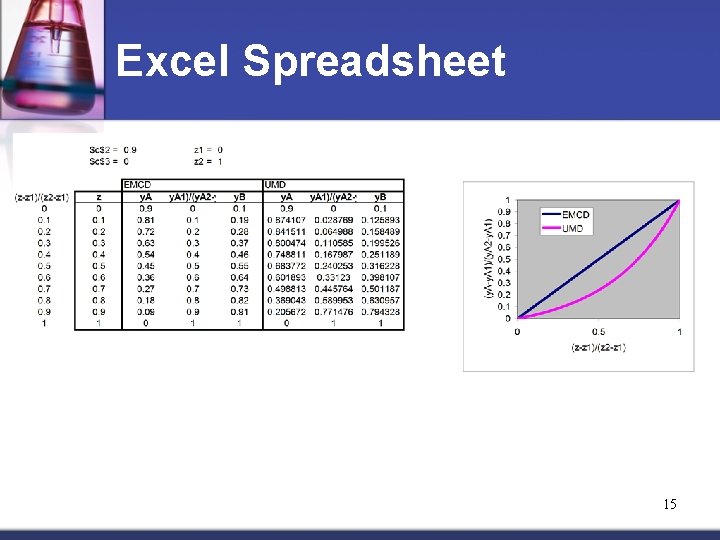
Excel Spreadsheet 15

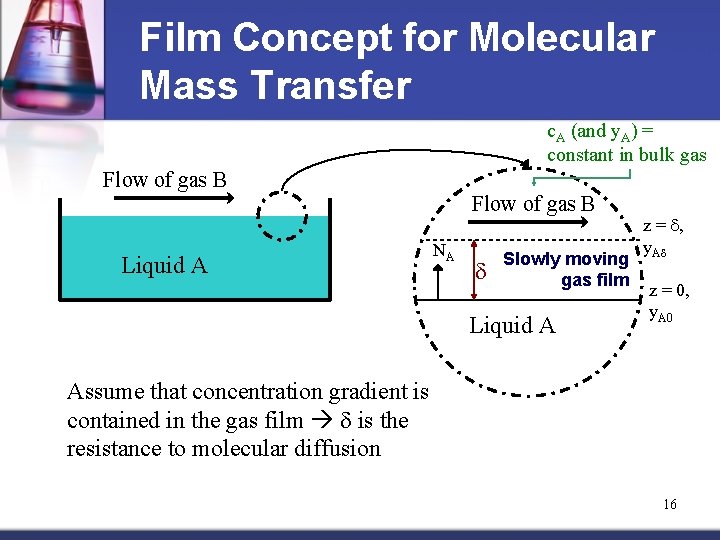
Film Concept for Molecular Mass Transfer c. A (and y. A) = constant in bulk gas Flow of gas B Liquid A Flow of gas B NA d Slowly moving gas film Liquid A z = d, y. Ad z = 0, y. A 0 Assume that concentration gradient is contained in the gas film d is the resistance to molecular diffusion 16

Generalization of Mass Transfer Forms EMCD UMD kc 0 and kc = film mass transfer coefficients for EMCD and UMD, respectively • If y. A is very small y. B ~ 1 y. B, lm ~ 1 • At low concentrations of A, UMD ~ EMCD 17

Application: Pseudo Steady State Diffusion of A Through Stagnant Film of B n n Recall the Arnold Diffusion Cell Same assumptions as before EXCEPT that z 1 decreases with time as A evaporates diffusion path length changes n If change in z 1 from time t 0 to t 1 is negligible diffusion path is constant NA ~ constant “pseudo steady state” n At pseudo steady state, small changes in level (z 1) over a large period of time n Note that NA does not depend on the amount of liquid or the cross sectional area 18

n Recall n Also, at pseudo steady state consider that: Rate of evaporation of A = w = Across* NA n In terms of liquid mass balance: n n Equating the two equations, and solving for NA: 19

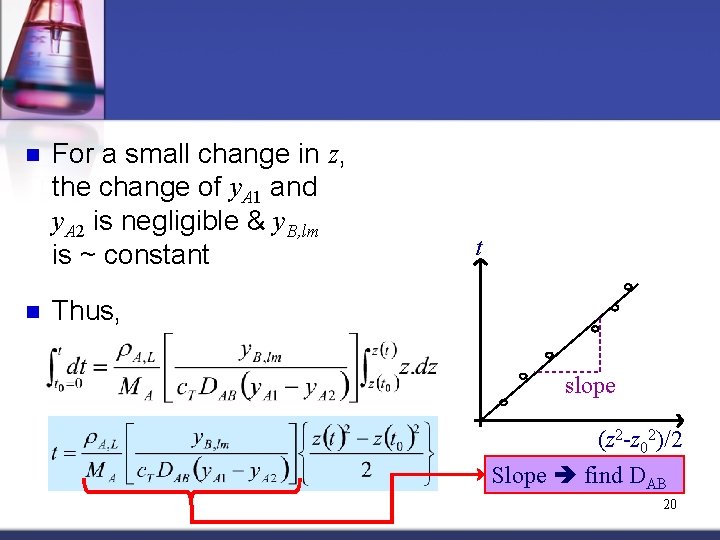
n n For a small change in z, the change of y. A 1 and y. A 2 is negligible & y. B, lm is ~ constant t Thus, slope (z 2 -z 02)/2 Slope find DAB 20

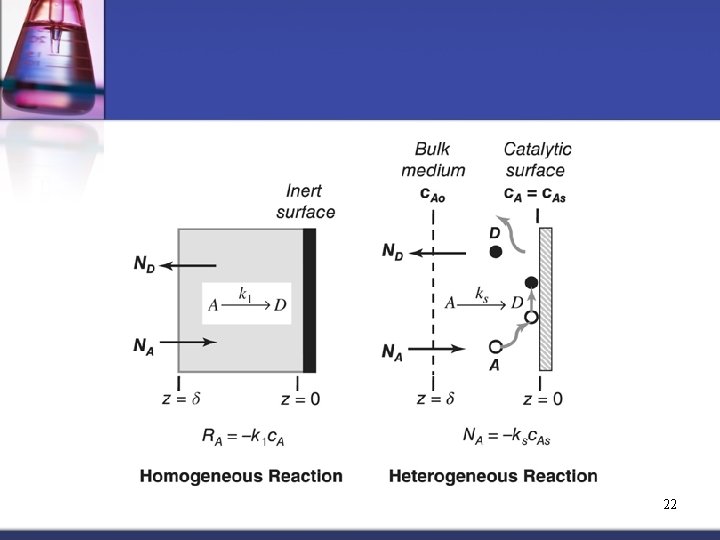
Chemical Reactions Two types of Chemical Reactions: 1. Heterogeneous Reaction affects only the BCs: n n n 2. Reactant which is consumed Product which is formed Catalyst which promotes reaction(s) of component(s) in the fluid but is neither consumed or formed Homogeneous Reaction: Reaction which occurs within a single diffusion phase where the reactants and products are consumed and formed within 21 the phase

22

1 D Mass Transfer with 1 st Order Homogeneous Chemical Reaction Consider diffusion and reaction of solute “A” within liquid film containing solvent “B” n In the liquid, a homogeneous reaction occurs where “A” decomposes to produce “C” n A C The 1 st order rate equation: Rate of generation of A Because “A” is consumed RA = – k 1 c. A 1 st order rate constant (sec-1) 23

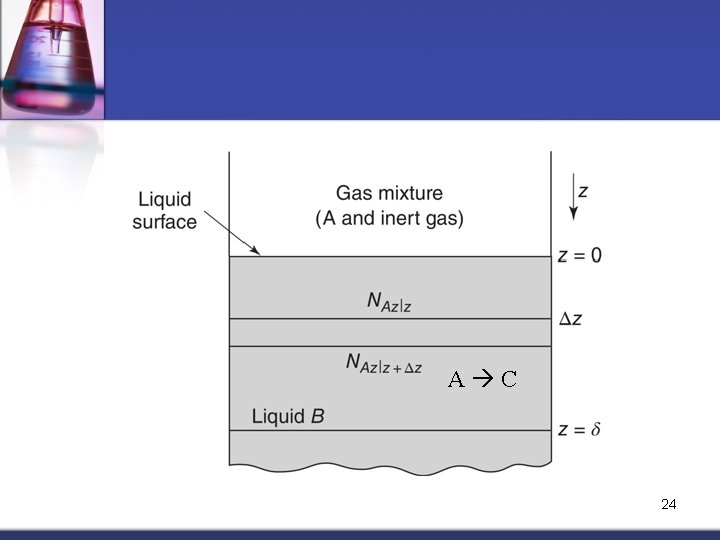
A C 24

n Focus All Analyses on Liquid Phase Differential Flux Equation: General Flux Equation: § § If no sink for “C” Nc = 0 UMD of “A” If there is very little fluid motion within the film, and if the concentration of A in the film is assumed dilute, then the molar flux within the film is described by 25

n Substituting flux equation into the differential equation: Boundary Conditions: [1] c. A = c. A 0 @ z = 0 (surface) [2] c. A = 0 @ z = d (position in liquid film when all “A” is consumed 26

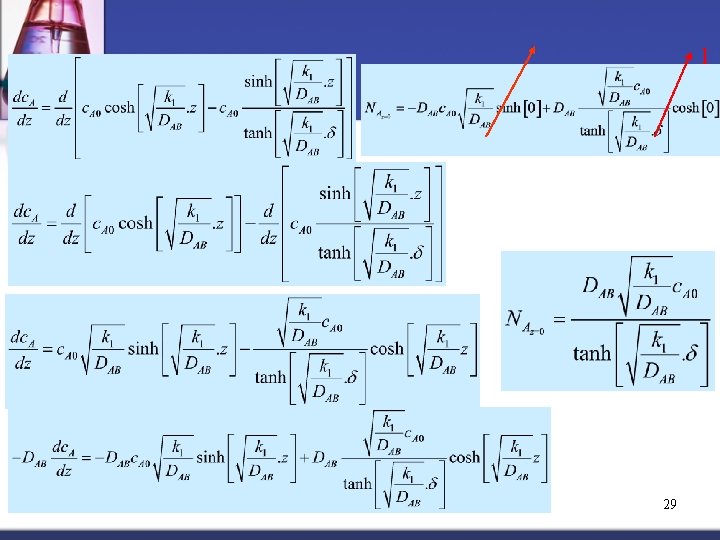
n General solution of 2 nd order ODE: 27

n Getting flux at surface (z = 0) by differentiation of c. A Ha = Hatta Number (dimensionless) 28

1 29

n For large k 1 30

Exercise Silicon thin films are formed at high T (900 K) and low P (100 Pa) by the reaction: Si. H 4(g) Si (s) + 2 H 2(g) The surface reaction is very rapid. As a result, the diffusion of Si. H 4(g) to the surface is the rate limiting step. The gas space over the growing film is quiescent. Develop a differential model for this process, including statements of assumptions and boundary conditions. Si. H 4 (g) + N 2 (g) z=0 Si. H 4 To Vacuum H 2 z=d 31

Solution n Si. H 4 is the source, Si film is the sink n Reaction only at surface, no reaction in diffusion path, RA = 0 Feed provides Si. H 4 in excess the concentration of Si. H 4 is constant at z = 0 Flux is in 1 D along z axis of rectangular coordinates d is very small compared to diffusion path Mass transfer is steady state: n n Flux is constant in the z-direction 32

Solution (Continued) Flux Equation From Stoicheometry: 1 mole Si. H 4 (A) produces 2 moles H 2 (B) NBz = - 2 NAz Boundary Conditions: 1: y. A= y. A 0 @ z=0 2: y. A= y. As @ z = d Find the expressions for the concentration profiles 33